电动汽车减速器壳体变形与传动误差联合试验研究

2022-03-15郭栋申志朋葛帅帅黎洪林石晓辉

机械科学与技术 2022年1期

郭栋,申志朋,葛帅帅,黎洪林,石晓辉

(重庆理工大学汽车零部件先进制造技术教育部重点实验室,重庆 400054)

国内电动汽车市场持续扩大,汽车朝高速化、轻量化和电动化的方向发展,随着三化的持续推进,电动汽车减速器服役工况和工作条件越来越复杂,使得壳体刚性不足、变形过大等缺点逐步凸显,带来了减速器啸叫等NVH问题[1]。传动误差作为汽车传动系统振动和噪声的重要激励源,引起了学者的广泛关注[2-4]。邓效忠等[5]建立了行星轮系齿轮的几何模型,根据齿面接触分析、承载接触分析技术和行星轮相位差的概念提出了传动误差的计算方法,利用该方法预测了行星轮系和直廓内齿轮的传动误差随扭矩变化趋势。唐进元[6]提出了传动误差计算的概念模型和力学模型,并推导出传递误差与制造误差、受载变形、动载荷和齿轮几何参数的关系。郭栋等[7]提出了多级传动误差的理论计算方法,对某二级减速器的传动误差进行了预测,并进行试验,验证了预测结果的准确性。汪中厚等[8]利用有限元对螺旋锥齿轮的静传动误差和动传动误差进行仿真,对传动误差随扭矩的变化规律进行了预测。陈洪月等[9]构建了齿廓修形的齿轮传动误差数学模型以及齿廓修形优化模型,以此模型计算得到了某个齿轮副传动误差的最优修形量。林家春等[10]采用TCA分析方法,预测了偏置距对正交面齿轮传动误差的影响规律,进行不同偏置距下的面齿轮传动误差测量试验,验证了预测规律的准确性,提出了减小传动误差的安装原则。袁古兴等[11]推导了考虑偏心误差的少齿差滤波减速器传动误差计算方法,进行试验,验证了所提出方法的准确性。严宏志等[12]用有限元法得到了不同相对位置的螺旋锥齿轮传动误差和接触斑点,并进行传动误差和接触斑点测试,验证仿真结果,指出螺旋锥齿轮传动误差对小轮安装误差更敏感。

近年来,有学者开始研究壳体变形对传动误差的影响,获得了壳体变形对传动误差影响的部分成果,但对二者相互关系的研究还不够深入,更缺乏试验支持[13-14]。为此,本文以某款国产电动汽车减速器为研究对象,在传动误差试验台架上进行减速器壳体变形和传动误差的同步联合试验;对不同扭矩下壳体变形与传动误差进行同步统计,探寻壳体变形和传动误差随负载变化规律,并进一步探索壳体变形与传动误差的相互影响,以丰富传动误差的理论体系。

1 测试原理

1.1 传动误差

传动误差定义为:当主动齿轮转动一个角度,从动齿轮的实际转角与理论转角之间的差异,可以用转角差或线位移差来表示[15]。传动误差的影响因素很多,如轮齿变形、修形、加工制造误差、安装误差和传动系统受载变形等[16]。根据计算方式的不同可以把传动误差分为总体传动误差和单体传动误差。

总体传动误差为

TE=rg(θg-θp/i)

(1)

单齿传动误差为

ΔTE=TEk-TEk-n=

(2)

式中：rg为从动齿轮节圆半径;θg为从动齿轮实际转角;θp为主动齿轮转角;i为由输入齿轮到输出齿轮的传动比;k为第k次测量;n为采用滑动计算方法的跨点数步长,一般不得跨越半齿数所对应的脉冲数。

总体传动误差是一种累积误差,反应了齿轮副传递运动和动力的综合能力,而单齿传动误差是一种实时误差,反应每个时刻齿轮副的啮合性能,二者反馈了不同的啮合状态信息[17]。

1.2 壳体变形

当传动系统受载转动时,根据单齿传动误差ΔTE和啮合刚度km可以得到轮齿每一时刻的切向啮合力为

Fmt=ΔTE·km

(3)

根据图1的受力分析可以得出齿轮的切向啮合力和径向啮合力的合力,即齿轮对轴的径向力为

Fmr=Fmt/cosαt

(4)

式中αt为端向压力角。

轴向啮合力为

Fma=Fmt·tanβ

(5)

式中β为螺旋角。

对输入轴进行受力分析,得到各个轴承的轴向力和径向力,其值都是单齿传动误差的线性表达,中间轴和输出轴的轴向力和径向力以同样的方式计算得到,最终可以得到各个轴承的轴向力Fia和径向力Fir的表达形式,即：

Fia=λia×ΔTE

(6)

Fir=λir×ΔTE

(7)

式中：λia、λir分别为轴承轴向和径向系数。

在所有轴承轴向力Fia和径向力Fir综合作用下壳体将发生轴向和径向的变形。

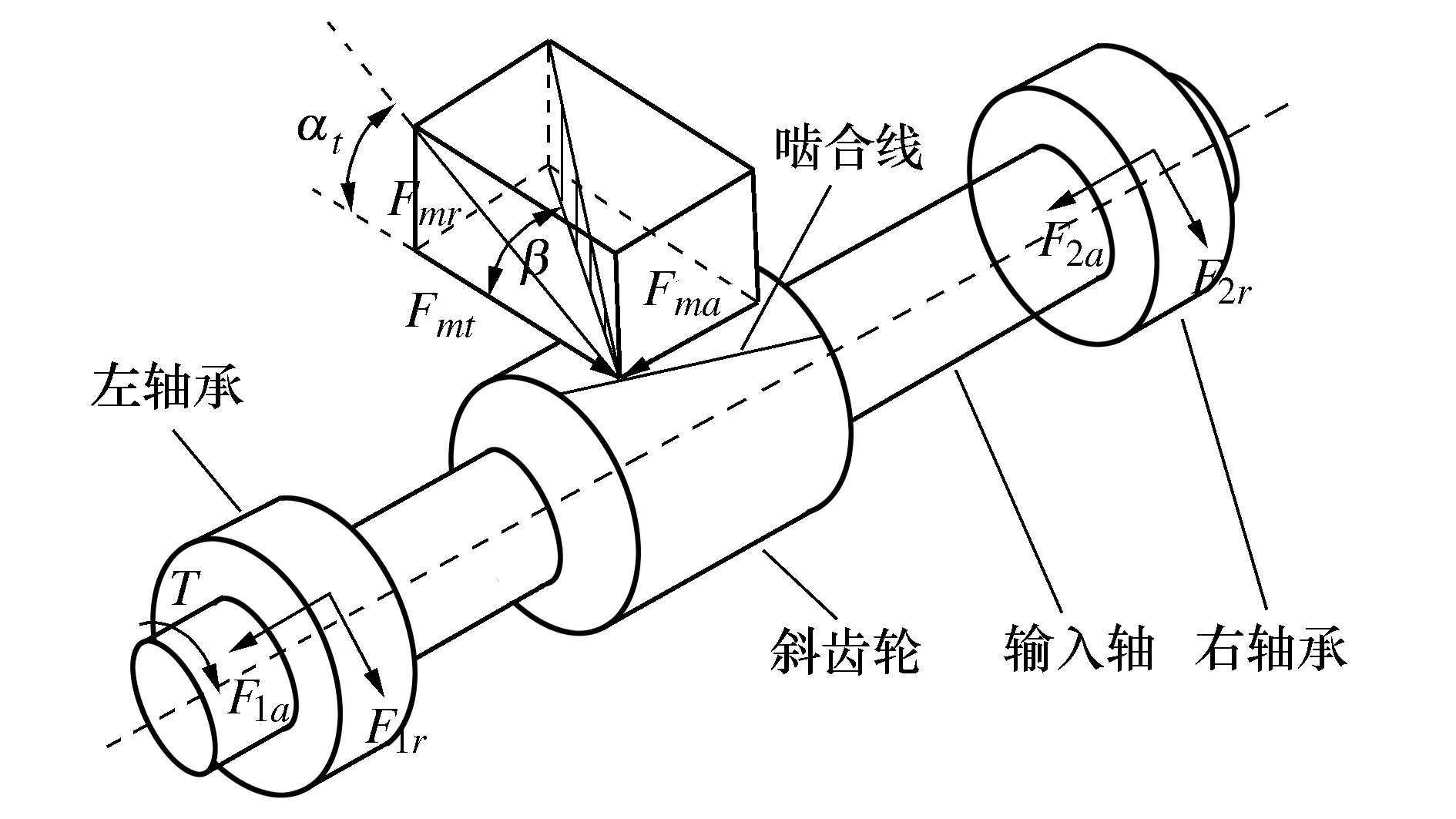
图1 输入轴受力简图

1.3 测试原理

将被试件搭载在传动误差试验台上进行传动误差和壳体变形采集,测试原理如下:

1) 传动误差测试。在输入轴和输出轴的末端安装精密角位移传感器,同步采集输入轴和输出轴的转动角度,根据式(1)和式(2),分别计算得到总体传动误差和单齿传动误差;

2) 壳体变形测试。在壳体选择合适的指针位移传感器布点,同时采集壳体表面轴向和径向位移,壳体的轴向变形量和径向变形量计算式为：

δia=xia-xia0

(8)

δir=xir-xir0

(9)

式中:xia0为初始轴向位移;xir0为初始径向位移;xia为变形后轴向位移;xir为变形后径向位移;δia为壳体轴向变形量;δir为壳体径向变形量。

整个测试系统包括驱动系统、负载系统、被试减速器、传感器、数据采集系统和控制系统等。试验的测试原理图见图2。

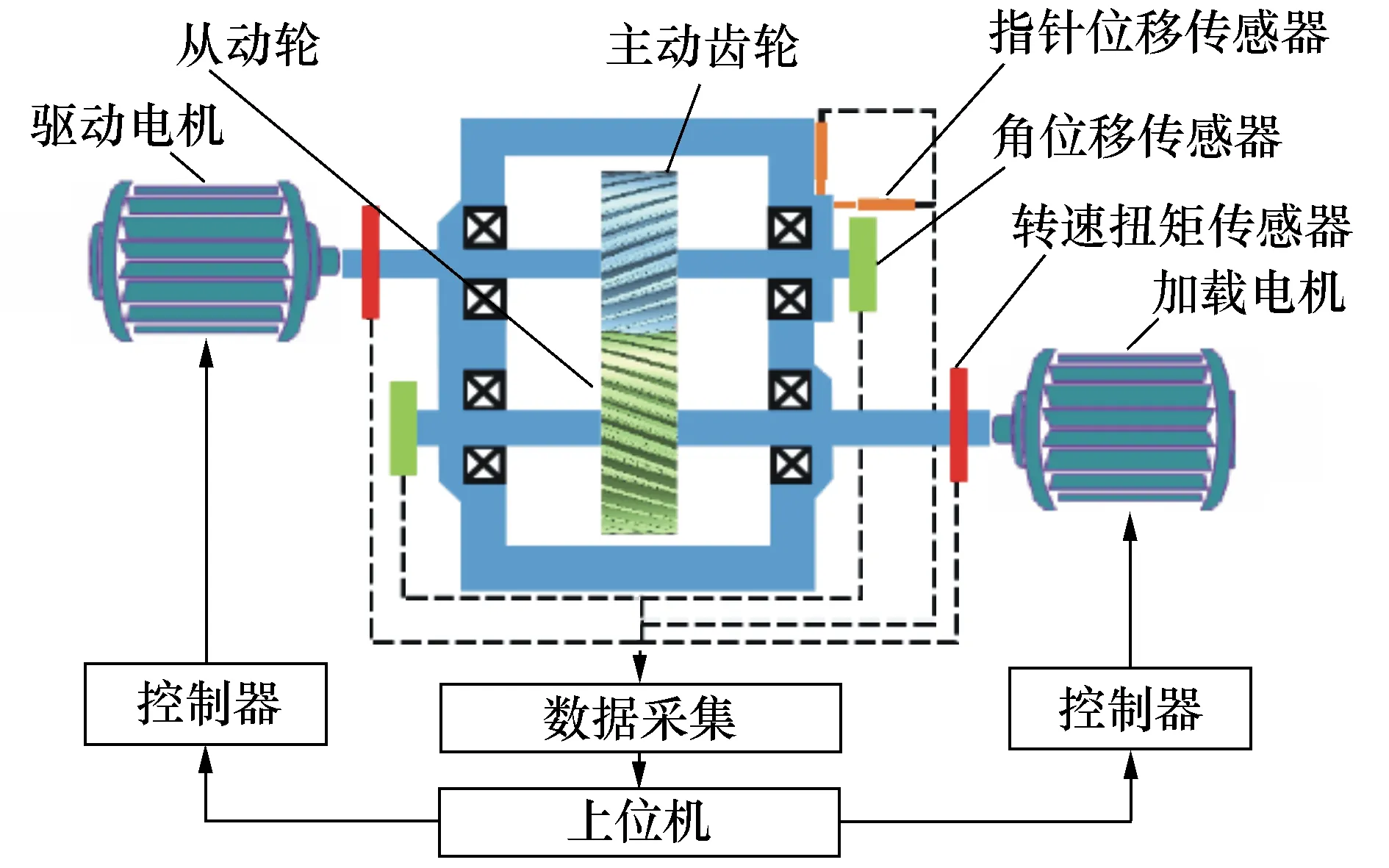
图2 试验测试原理图

2 试验对象及装置

试验对象为二级单速比电动汽车减速器,减速器参数见表1。

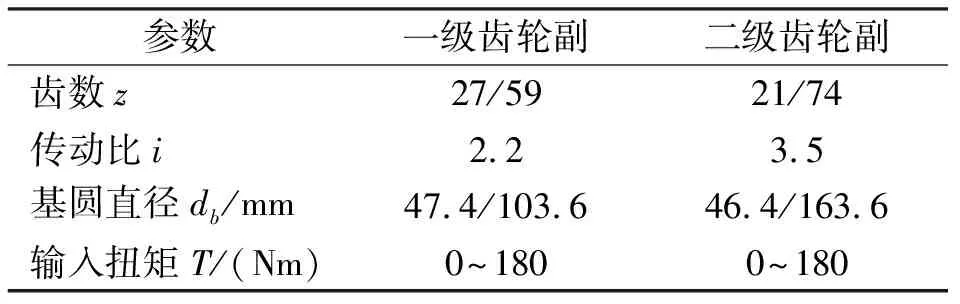
表1 减速器参数

将其搭载在传动误差试验台上,传动误差试验台的实物图如图3所示。

图3 传动误差台架实物图

传动误差台架由驱动电机、联轴器、被试减速器、转速扭矩传感器、角位移传感器、指针位移传感器和负载电机等部分组成，各位移感器参数见表2。

表2 传感器参数

各位移传感器的布置位置说明如下:

1) 试验采用3个角位移传感器,分别测量输入轴、中间轴和输出轴的转角;

2) 减速器齿轮的啮合力通过齿轮、轴和轴承传递到壳体,壳体在轴承孔位置处变形突出,并综合考虑壳体表面的结构特征和布置难易等因素,选择了如图4所示的布点进行指针位移传感器布置,各测点的具体说明见表3。

图4 指针位移传感器测点布置

表3 指针位移传感器布点说明

3 试验结果及讨论

根据汽车在不同的场景行驶时传动系统的不同旋转方向和加载情况,制定了表4的测试工况,进行传动误差和壳体变形的同步联合试验。

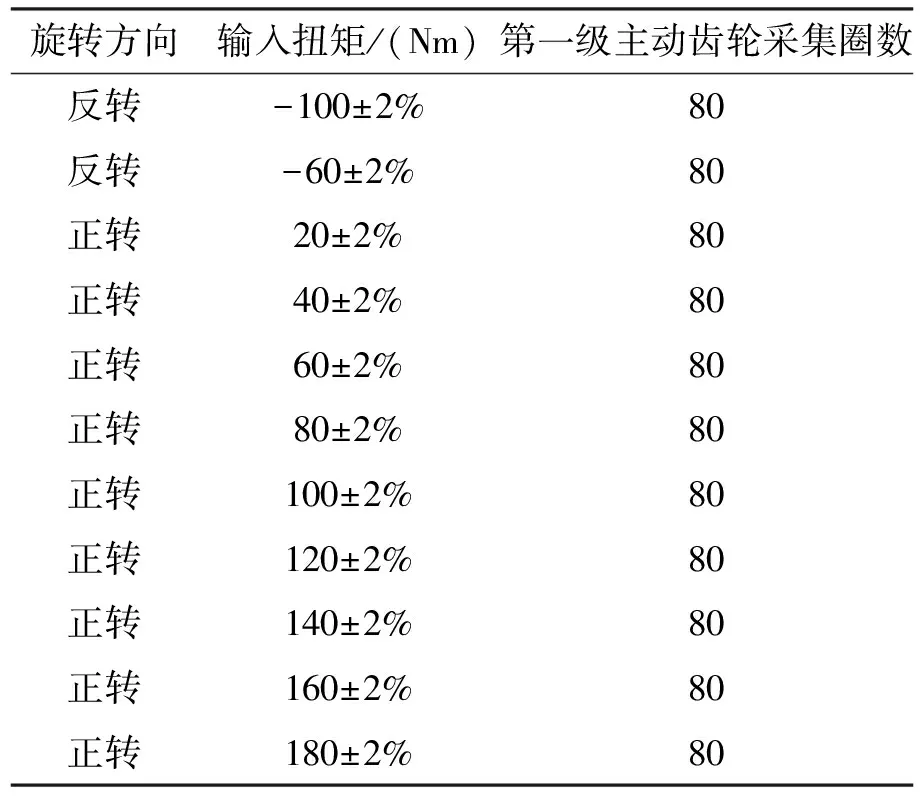
表4 测试工况

3.1 传动误差和壳体变形信号的时频分析

对所有的结果进行频谱分析,并以输入轴频率为参考,发现各扭矩下各级传动误差、各测点变形的频率成分基本一致,不同之处体现在各频率点幅值的变化上。图5和图6是120 Nm下的第一级齿轮副总体传动误差、第一级齿轮副单齿传动误差。

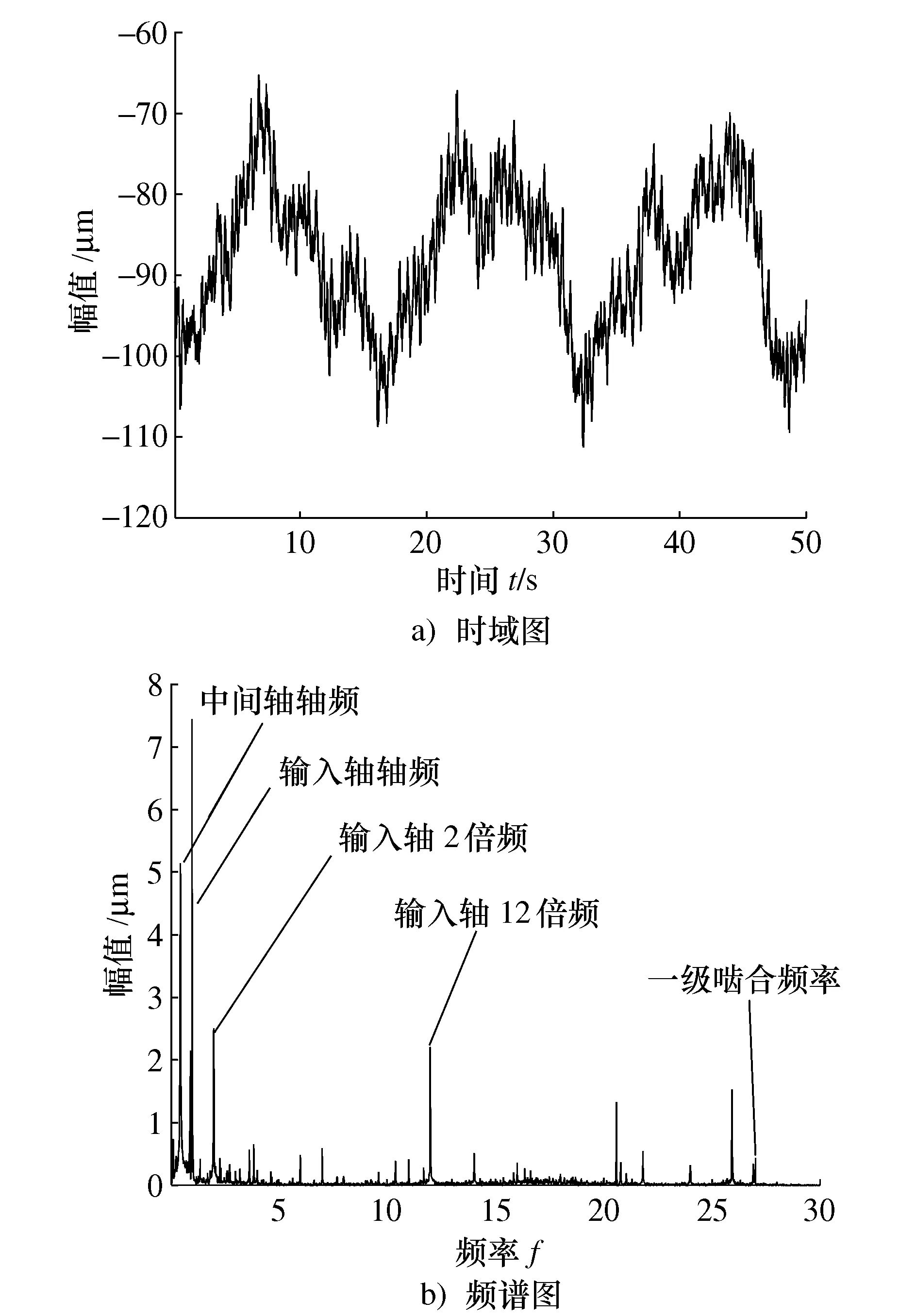
图5 120 Nm第一级齿轮总体传动误差

从第一级总体传动误差时域图5a)中可以看出，该信号由几个幅值较大的长周期信号和一些小幅值短周期信号构成,这也反映了第一级总体传动误差的成分复杂,包含了丰富的信息。对时域信号进行傅里叶变换,得到其频谱见图5b),幅值较为集中的分布在0～27倍轴频的低频段,中间轴轴频、输入轴轴频和输入轴谐频处的幅值较为突出,而第一级啮合频率处的幅值较低约0.5 μm。

从第一级齿轮副单齿传动误差的时域图6a)中看出,该信号的峰峰值远小于第一级总体传动误差的峰峰值,且没有幅值较大的长周期信号,相反,短周期信号的幅值较大。对时域信号进行频谱分析,见图6b),在1～200倍轴频的范围内均有明显的幅值分布,如图6b)所示,其中幅值较为明显的皆为各轴的谐频,且最大幅值出现在较高的频段,基频处的幅值不明显,第一级啮合频率处的幅值相对较小约0.05 μm。

120 Nm下的第二级总体传动误差见图7。与第一级总体传动误差相似,第二级总体传动误差同样是由多个幅值较大的长周期信号和一些小幅值短周期信号构成,第二级总体传动误差峰峰值要大于第一级总体静态传动误差峰峰值。对时域信号进行傅里叶变换,幅值较为集中的分布在0～27倍轴频的低频段,其中输出轴轴频处幅值最为突出,而二级啮合频率处的幅值约4.3 μm。

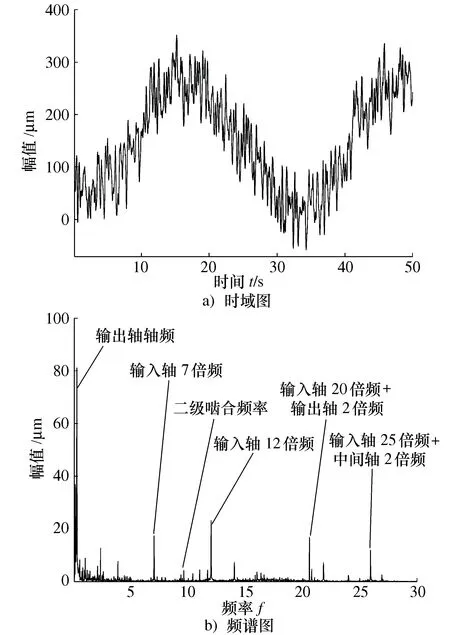
图7 120 Nm第二级齿轮总体传动误差

120 Nm第二级齿轮单齿传动误差如图8所示，其峰值同样远小于第二级总体传动误差的峰峰值,存在大量的短周期成分,但大于第一级单齿传动误差的峰峰值。对时域信号进行频谱分析,在1～200倍轴频的范围内均有幅值分布,如图8b)所示,输入轴谐频和其中某两根轴谐频组合处的幅值较为明显。各传动轴基频和第二级啮合频率处的幅值不明显。

总体传动误差是单齿传动误差的累积结果,随着采集的持续进行,一些信号进行了叠加,而另一些信号发生了抵消[18]。通过对上面各级总体传动误差和单齿传动误差进行对比分析,可以发现:

1) 对于第一级齿轮:与输入轴基频、中间轴基频、一级啮合频率、某些输入轴谐频、中间轴谐频和输出轴谐频有关的低频信号幅值进行了叠加,另一些与输入轴谐频、中间轴谐频和输出轴谐频有关的中高频信号幅值发生了抵消,从而造成第一级总体传动误差的幅值较为集中的分布在低频段内;

2) 对于第二级齿轮:与输出轴轴频、二级啮合频率、部分输入轴谐频、中间轴谐频和输出轴谐频有关的低频信号进行了叠加,另一些与输入轴谐频、中间轴谐频和输出轴谐频有关的中高频信号发生了相互抵消,第二级总体传动误的幅值也集中分布在低频段内。

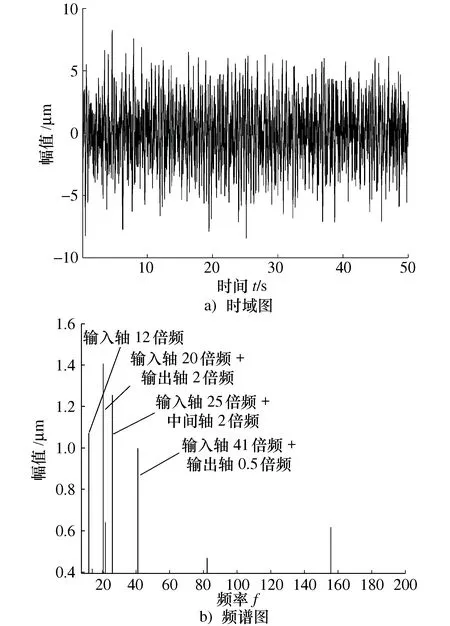
图8 120 Nm第二级齿轮单齿传动误差

120 Nm下的输入轴测点径向变形的时域曲线和频谱如图9所示。

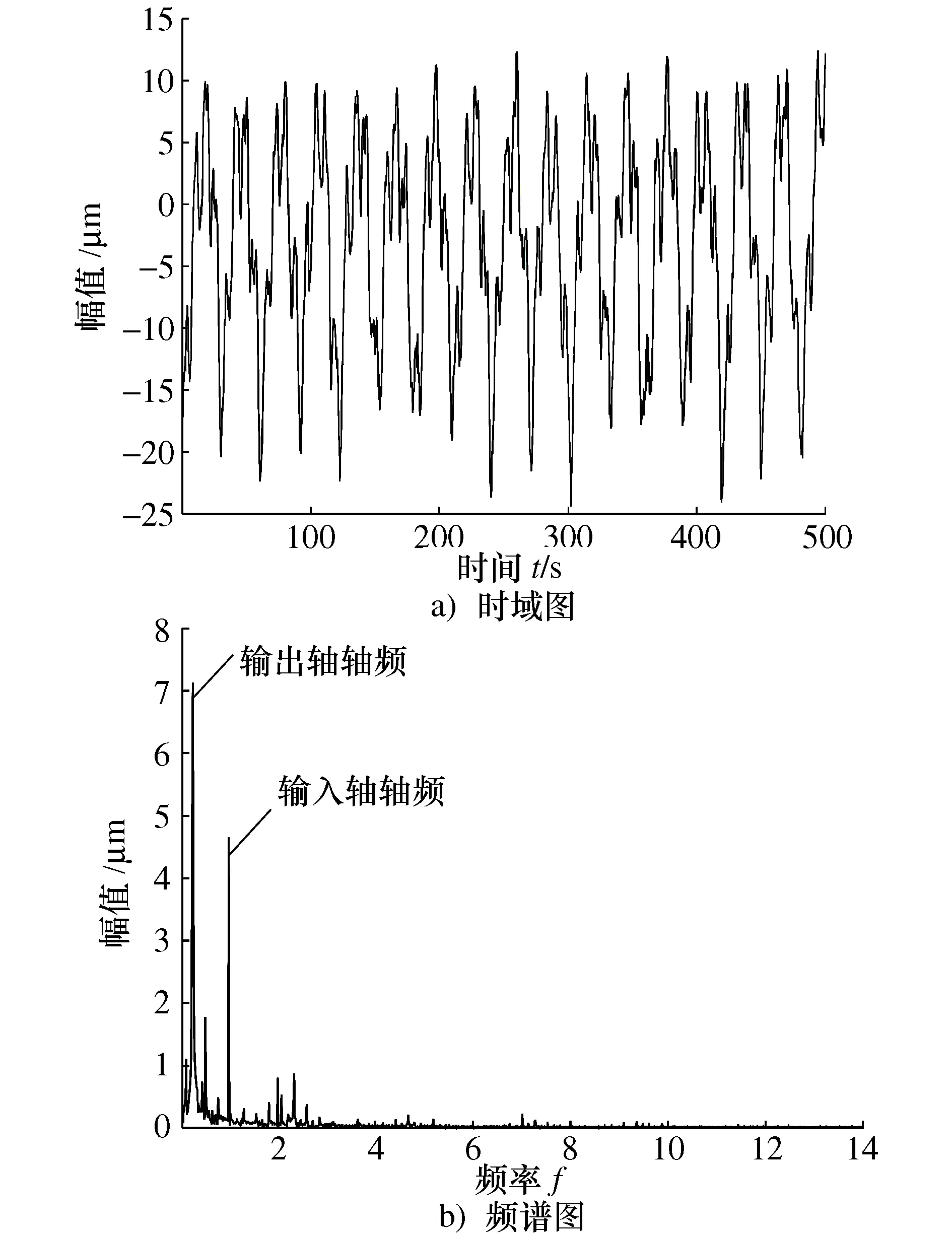
图9 120 Nm测点1输入轴径向变形量

从输入轴壳体径向变形时域图(图9a))可以看出,该信号主要由一些幅值较大的长周期信号组成,对时域信号进行频谱(见图9b))分析,,能看出这些信号的幅值集中分布在0～4倍输入轴频率的低频段,其中幅值贡献较大的两个频率为输入轴和输出轴基频,值得注意的是这两个频率也分别是第一级和第二级总体传动误差频谱中幅值贡献最大的频率点。

根据式(6)和式(7),探究传动误差对壳体变形的影响宜从单齿传动误差对壳体变形作用关系的角度出发;根据壳体变形的频谱显示,输入轴和输出轴轴频是壳体变形频谱的主要成分,而总体传动误差恰好低频突出,所以探究壳体变形对传动误差的影响宜从壳体变形对总体传动误差作用关系的角度出发。

3.2 单齿传动误差与壳体变形的关系

对各扭矩下各级齿轮副单齿传动误差峰峰值和各测点的壳体变形峰峰值进行同步统计,结果见表5。

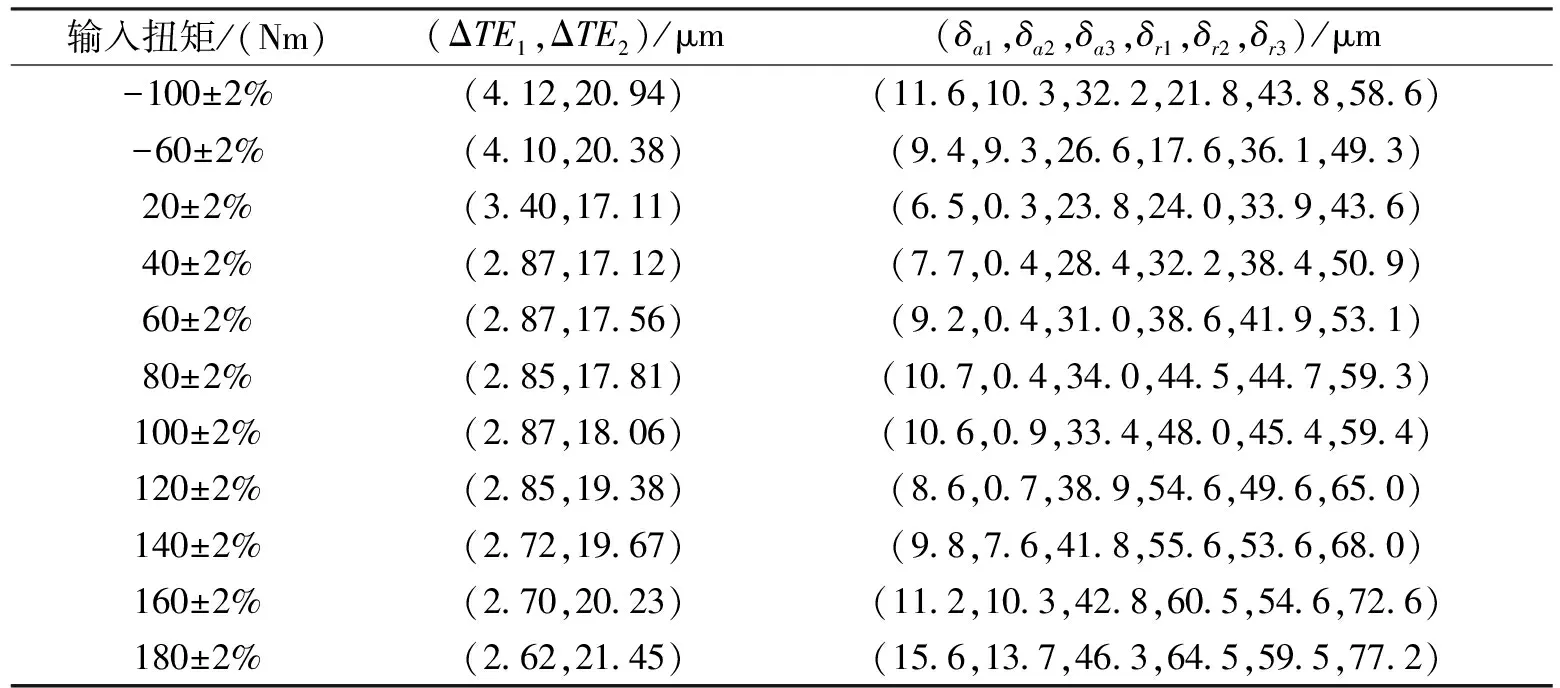
表5 单齿传动误差ΔTE和壳体变形δ峰峰值

同扭矩下反转的单齿传动误差和壳体变形量要明显大于正转,主要是正、反齿面的轮齿误差和修形不同,导致反转时单齿传动误差较大,壳体各测点的变形量也较大。正转各扭矩下的单齿传动误差和壳体表面各测点变形量存在一定的规律,见图10。

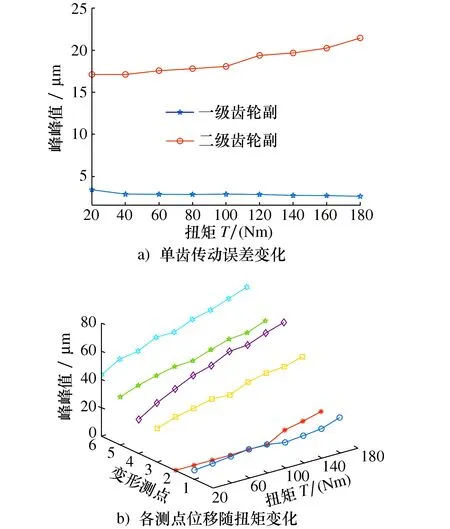
图10 单齿传动误差和壳体变形随扭矩变化

从图10a)中可以看出:第一级单齿传动误差呈现出相对稳定的趋势;第二级单齿传动误差随扭矩增加而同步增加,且其对扭矩变化相对敏感。第二级单齿传动误差峰峰值都在15 μm以上,要远大于第一级单齿传动误差峰峰值。呈现出这样的规律是由于在20～180 Nm的扭矩范围内,第二级齿轮副啮合力较大,第二级单齿传动误差以变形为主,而第一级单齿传动误差以误差为主[19]。

在20～180 Nm范围内,各测点变形量峰峰值变化趋势见图10b),可以看出:

1) 各测点的变形量随扭矩增加都呈现出递增的趋势,径向测点变形δr普遍大于轴向测点变形δa,同时,输出轴的径向测点变形δr3和轴向测点变形δa3也分别是所有径向测点变形和所有轴向测点变形中最大的。产生这样结果的原因是输出轴轴承力大于其他轴轴承力,且各轴承的径向力大于轴向作用力,同时离轴承孔越近的壳体表面受该处轴承处作用力的影响越大;

2) 各测点变形量对扭矩的曲线接近于线性,输入轴轴向测点变形δa1和中间轴轴向测点变形δa2相对较小,同时这两个变形曲线斜率也很小,说明输入轴和中间轴轴向变形对20～180 Nm范围内的扭矩变化不敏感。输入轴径向测点变形δr1在20～80 Nm范围内小于中间轴径向测点变形δr2,而在100～180 Nm范围内二者大小相反,但输入轴径向测点变形δr1的斜率大于中间轴径向测点变形δr2的斜率,即输入轴径向测点变形δr1对该范围内的试验扭矩变化更敏感。

各测点变形量的变化趋势与第二级单齿传动误差变化趋势是一致的,这是因为各扭矩下的第二级单齿传动误差峰峰值要远大于第一级单齿传动误差峰峰值,根据式(6)和式(7)可知,输出轴轴承对壳体的作用力要远大于输入轴轴承对壳体的作用力,导致第二级齿轮副单齿传动误差对壳体变形的作用会掩盖住第一级齿轮副单齿传动误差的作用,最终壳体各点变形趋势和第二级单齿传动误差随扭矩变化趋势保持一致。

3.3 壳体变形与总体传动误差的关系

传动误差描述的是两个啮合齿轮沿啮合线方向相对位置变化,所以壳体变形对传动误差的影响直接体现在两啮合齿轮轴线的相对位置变动上[20]。

输入轴和中间轴轴承孔处的轴向和径向相对位移分别为：

δ1=δa1-δa2

(10)

δ2=δr1-δr2

(11)

中间轴和输出轴轴承孔处的轴向和径向相对位移分别为：

δ3=δa2-δa3

(12)

δ4=δr2-δr3

(13)

据图5和图7的分析中得知,第一级总体传动误差频谱中输入轴轴频处的幅值贡献最大,第二级总体传动误差频谱中输出轴轴频处的幅值贡献最大。为此,为了探究壳体变形对传动误差的影响,对正转各扭矩下各级齿轮副的总体传动TE1和TE2峰峰值进行统计,见图11;对轴承孔处相对位移δ1、δ2、δ3和δ4的峰峰值,δ1和δ2频谱中输入轴基频处的幅值和δ3和δ4频谱中输出轴基频处的幅值进行统计,见图12。

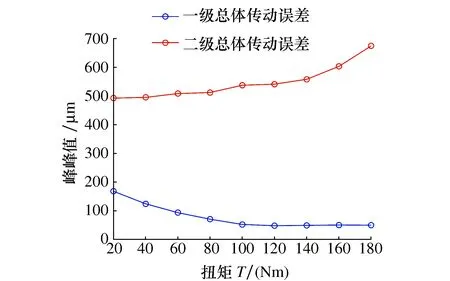
图11 各级齿轮副总体传动误差随扭矩变化

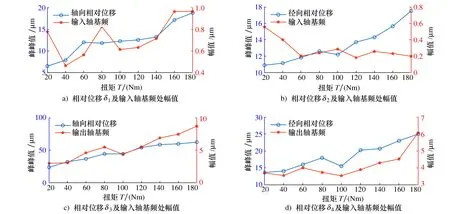
图12 相对位移和特征频率处幅值随扭矩变化

图11展示了各级总体传动误差随扭矩的变化规律：第一级总体传动误差在20～100 Nm扭矩范围内随扭矩增加呈明显地降低的趋势,从100 Nm开始其对扭矩的敏感度降低,曲线趋于平稳;第二级总体传动误差在20～100 Nm扭矩范围内随扭矩增加而平稳上升,从120 Nm开始其对扭矩的敏感度逐渐增加,其峰峰值急剧上升。第二级总体传动误差峰峰值基本在500 μm以上,远大于第一级总体传动误差。呈现这样的趋势同样是由于轮齿变形对第二级总体传动误差贡献突出,误差对第一级总体传动误差作用突出。这种趋势与图10a)各级单齿传动误差的变化趋势相近,这也说明了总体传动误差和单齿传动误差的联系,即总体传动误差是单齿传动误差进行累积后的结果。

对比图12a)和图12b)可以发现:同扭矩下,轴承孔处轴向相对位移δ1和径向相对位移δ2相差不大, 二者的峰峰值都随扭距的增加而增加。δ1频谱中输入轴基频处幅值大体呈现递增趋势,个别扭矩点有一些波动;δ2频谱中输入轴基频处幅值随扭矩增加呈现递减的趋势,且其对扭矩的敏感程度也随扭矩增加而降低,这与第一级总体传动误差峰峰值的变化趋势相近。

对比图12c)和图12d)可以发现δ3和δ4的峰峰值都是随扭矩的增加而增加,同扭矩下,轴承孔处轴向相对位移δ3大于径向相对位移δ4。δ3和δ4频谱中输出轴基频处幅值随扭矩增加都呈现出增加的趋势,但轴承孔处径向相对位移δ4频谱中输出轴基频处幅值对扭矩的敏感程度逐渐增高,这与第二级总体传动误差的变化趋势相近。

对比图11和图12的结果可以发现,壳体变形与总体传动误差的关系主要体现在:

1) 对于各级齿轮副,轴承孔处径向相对位移对总体传动误差的影响大于轴向相对位移对总体传动误差的影响,这主要是由于该减速器大齿轮的齿宽大于小齿轮的齿宽,当发生轴向相对移动时,并不会影响实际的工作齿宽,所以轴向相对位置变化对总体传动误差的影响较小。为减小传动误差、优化减速器NVH性能,提升壳体轴承孔处的径向刚度是一种可行的方案;

2) 壳体轴承孔处的相对变形量主要是由输入轴基频和输出轴基频两种频率信号组成,总体传动误差变化趋势与壳体轴承孔处径向相对位移频谱中这两处频率的幅值变化趋势紧密相关。如第一级总体传动误差频谱中最大幅值出现在输入轴基频处,壳体轴承孔处径向相对位移δ2频谱中同样存在这一频率,且在不同扭矩下第一级总体传动误差变化趋势和壳体轴承孔处的径向相对变形量δ2频谱中输入轴基频处的幅值变化趋势一致。