例谈导数中与构造函数有关的两类问题
2022-03-14杨生华舒巧云
杨生华 舒巧云
(湖南省怀化市铁路第一中学)
导数与不等式有关的求解及证明是高考的重点,而学生在构造函数方面的能力较弱.高考中导数题具有较大的难度,其中一部分原因源于学生对函数的构造欠缺思考.在2020年的高考中,与导数有关的函数构造在绝大多数省份数学压轴题中均有体现.为提高学生在构造函数方面的能力,本文通过实例,对构造函数求解不等式问题和构造函数证明与对数有关的不等式问题进行了探讨.
1 构造函数求解不等式问题
常见的构造函数策略:
1)f′(x)-g′(x)>0↔F(x)=f(x)-g(x).
2)xf′(x)-f(x)>0↔F(x)=
3)f′(x)+f(x)>0↔F(x)=exf(x).
4)f′(x)-f(x)>0↔F(x)=
5)(x+1)f(x)+xf′(x)>0↔
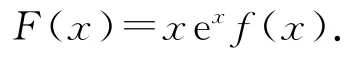
6)f′(x)xlnx+f(x)>0↔F(x)=f(x)lnx.
例1设定义域为R 的函数f(x)的导函数为f′(x),且满足f′(x)<f(x),且f(x+2)为偶函数,f(4)=1,则不等式f(x)<ex的解集为_________.


所以F(x)在R上单调递减.
因为f(x+2)为偶函数,所以f(-x+2)=f(x+2),所以f(x)关于x=2 对称,所以f(0)=f(4)=1,故F(0)=1.因为<1,所以F(x)<1,所以F(x)<F(0),即x>0.
综上,f(x)<ex的解集为(0,+∞).
例2若定义在R 上的函数f(x)满足f(x)+f′(x)>1,f(0)=4,则不等式f(x)>+1的解集为______.

构造函数F(x)=exf(x)-ex,则F′(x)=ex(f′(x)+f(x)-1)>0,所以F(x)在R上单调递增.不等式f(x)>+1可化为exf(x)-ex>3.因为f(0)=4,所以F(0)=3,则原不等式可化为F(x)>F(0),即f(x)>+1的解集为(0,+∞).
例3设函数f′(x)是奇函数f(x)(x∈R)的导函数,f(-2)=0,当x>0时,xf′(x)-f(x)<0,则不等式f(x)>0的解集为________.

构造函数F(x)=,故当x>0时,有

即F(x)在(0,+∞)上单调递减,而f(x)为R 上的奇函数,所以F(-x)==F(x),故F(x)为(-∞,0),(0,+∞)上的偶函数,所以F(x)在(-∞,0)上单调递增.
因为f(-2)=0,所以F(-2)=F(2)=0.
当x>0 时,f(x)>0⇔F(x)>0,即F(x)>F(2),从而x∈(0,2).
当x<0 时,f(x)>0⇔F(x)<0,即F(x)<F(-2),从而x∈(-∞,-2).
综上,f(x)>0的解集为(-∞,-2)∪(0,2).

1)例1、例3可直接根据题给条件形式构造函数.
2)例2中构造函数需要根据条件中的给定形式以及求解不等式的关系共同构造.
3)在求解过程中(如例1、例3),要根据具体条件,分情况讨论和分析函数图像的特点,再求解范围.
2 构造函数证明与对数有关的不等式问题
构造与对数有关的函数证明不等式源于人教A版高中数学《选修2-2》上第32 页习题:ex>1+x(x≠0)及lnx<x<ex(x>0),由此可以类推得到一些重要的不等式,为构造函数提供方向.

例4设m,n∈R*,且m>n,求证:


该题在构造函数时需要对所证明的不等式进行等价变换,再证明有关函数的单调性.
例5证明:

证明令F(x)=ln(x+1)-x,则F′(x)=故F(x)在(-1,0)上单调递增,在[0,+∞)上单调递减.
又F(0)=0,所以F(x)<F(0)=0(x>0),即ln(x+1)<x(x>0),令x=,则

证明由例5 可知ln(x+1)<x(x>0),即lnx<x-1(x>1).因为

所以当x∈[1,+∞)时,F(x)单调递减.而F(1)=0,所以当x∈(1,+∞)时,F(x)<0恒成立.故当n∈N*,n≥2时,有
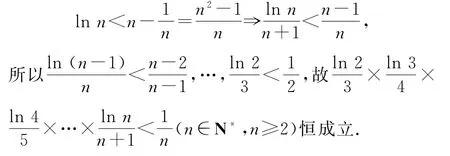

发现例6中要求证明的不等式右边是一个等差数列求和,因而在构造函数式时需要考虑累加法.
(完)
