函数不等式证明的常用方法

林国红

(广东省佛山市乐从中学)

纵观近几年高考试卷以及各级各类模拟考试试卷,函数不等式的证明是热门考点之一,常作为压轴题频频亮相,函数不等式具有综合性强、思维量大、方法繁多、技巧性强等特点,注重对能力和数学思想方法的考查,难度较大.下面以一道模拟考试题为例,从多个视角分析问题,以此归纳总结函数不等式证明的常用方法,供大家参考.

1 题目呈现与分析

题目已知f(x)＝xln(x＋a)＋1(a＜0).

(1)当a＝－1时,判断f(x)的单调性;

(2)证明:f(x)＜ex＋cosx.

分析试题分步设问,逐步推进.试题的第(1)问较为简单,只要能准确应用导数公式和求导法则就可以解决问题.试题第(2)问待证不等式中含有参数、指数函数、对数函数、三角函数,与2019年全国Ⅰ卷文科、理科的函数与导数题类似,都是与三角函数交会的题型,综合性较强.求解试题不但需要学生了解函数的单调性,而且要求学生会利用化归与转化等思想,对学生运用所学知识寻找合理的解题策略以及推理论证能力有较高的要求.总之,本题层次分明,区分度高,作为试卷的压轴题,是一道能突出选拔功能的好题.

由于第(1)问较为简单,本文不作讨论,下面从不同视角,给出第(2)问的几种证法.

2 证法探究

因为a＜0,故x＞－a＞0,所以

要证明f(x)＜ex＋cosx,只需证明xlnx＋1＜ex＋cosx,即证明xlnx＜ex＋cosx－1.当0＜x＜1时,因为ex＞1,cosx＞0,所以ex＋cosx－1＞0,xlnx＜0,故xlnx＜ex＋cosx－1.

下面只需证当x≥1时,xlnx＜ex＋cosx－1成立即可.

2.1 直接作差,构造函数

证法1当x≥1时,设

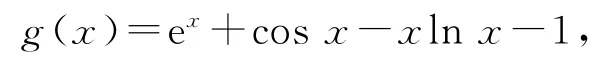
则g′(x)＝ex－sinx－lnx－1.令h(x)＝g′(x),则

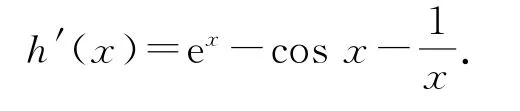
因为x≥1,故ex≥e,－1≤cosx≤1,0＜≤1,所以

于是h(x)在[1,＋∞)上单调递增,从而

即g′(x)＞0,所以g(x)在[1,＋∞)上单调递增.于是

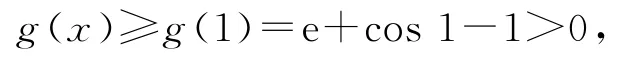
即xlnx＜ex＋cosx－1.

综上,当a＜0时,f(x)＜ex＋cosx.

一般来说,证明函数不等式f(x)＞g(x)恒成立,可设F(x)＝f(x)－g(x),则f(x)＞g(x)恒成立⇔F(x)＞0恒成立,即等价于Fmin(x)＞0.可以利用导数来求F(x)的最小值,把函数不等式的证明转化为利用导数研究函数的单调性或求最值.要注意的是,有时尽管F(x)存在最小值,但方程F′(x)＝0的根(F(x)的极值点)解不出来,往往要借助零点存在性定理和F′(x)的单调性,先证明方程F′(x)＝0有唯一实根x0,再用“设而不求”的方法,证明Fmin(x)＝F(x0)≥0,在运算过程中要注意利用F′(x0)＝0进行替换.

2.2 放缩法

证法2(利用lnx≤x－1放缩)因为lnx≤x－1(x≥0),当x＝1时,等号成立,所以

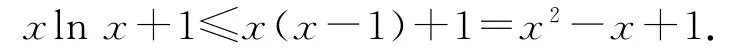
故只需证x2－x＋1＜ex＋cosx,即证

设g(x)＝ex－x2＋x－1(x≥1),则

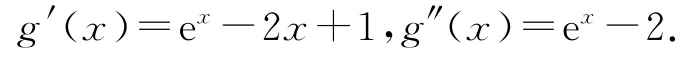
因为x≥1,所以ex≥e,故g″(x)＞0,从而g′(x)在[1,＋∞)上单调递增,所以

即g(x)在[1,＋∞)上单调递增.

当x∈[1,]时,cosx≥0,且

所以ex－x2＋x－1＋cosx＞0.

所以ex－x2＋x－1＋cosx＞0.

综上,ex－x2＋x－1＋cosx＞0,所以当a＜0时,f(x)＜ex＋cosx.

在证明函数不等式的压轴题中,有几个比较重要且常见不等式,如ex≥x＋1,ex≥ex,lnx≤x－1(x＞0),ex≥1＋x＋.此类函数的导数可以和多项式函数结合到一起,大部分都含有二次三项式,体现转化与化归思想;其次,此类函数能体现微积分的一个思想:以直代曲,无限逼近;另外,此类函数与高等数学的级数结合比较紧密.综上,以ex与lnx为背景的函数题,常用到这种思想方法.

证法3(利用cosx的有界性放缩)因为cosx≥－1(当x＝(2k＋1)π,k∈N 时,等号成立),所以ex＋cosx≥ex－1,故只需证xlnx＋1＜ex－1,即证ex－xlnx－2＞0.

设g(x)＝ex－xlnx－2(x≥1),则

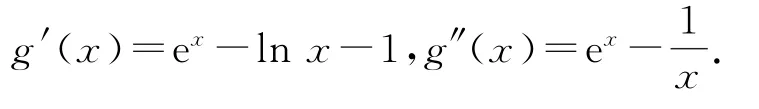
因为x≥1,所以ex≥e,0＜≤1,故g″(x)＝ex－＞0,从而g′(x)在[1,＋∞)上单调递增,于是

从而g(x)在[1,＋∞)上单调递增,于是

综上,当a＜0时,f(x)＜ex＋cosx.

综上,当a＜0时,f(x)＜ex＋cosx.

证法5由证法3可知,只需证xlnx＋1＜ex－1(x≥1),即证xlnx＜ex－2,两边同时除以x2,得

令q(x)＝ex(x－2)＋4(x≥1),则

于是q(x)在[1,＋∞)上单调递增,于是q(x)≥q(1)＝－e＋4＞0,即h′(x)＞0,所以h(x)在[1,＋∞)上单调递增,于是h(x)≥h(1)＝e－2,即hmin(x)＝e－2.又因为e－2＞,即

涉及与三角函数相关的不等式,往往可以利用三角函数的有界性进行放缩,即－1≤sinx≤1,－1≤cosx≤1,另外还要熟悉常见的三角函数不等式,如sinx＜x＜tanx(0＜x＜),0＜＜1(0＜x＜π)等.证法5用到了函数的“凹凸性反转”,即将要证不等式适当变形,一般是将原不等式中的ex与lnx分离,转化为两个函数h(x)与g(x).若h(x)存在最小值hmin(x),g(x)存在最大值gmax(x),且有hmin(x)＞gmax(x),则h(x)＞g(x)恒成立.需要说明两点:1)若hmin(x)＝gmax(x),hmin(x)＝h(x1),gmax(x)＝g(x2)且x1≠x2,显然h(x)＞g(x)恒成立;2)若h(x)不存在最小值,或g(x)不存在最大值时,可将要证不等式h(x)＞g(x)适当变形,等价转化为φ(x)＞ψ(x),若φmin(x)＞ψmax(x),则h(x)＞g(x)恒成立.这种通过分离ex与lnx来构造两个函数,再分别求所构造函数的最值来证得原不等式的方法,往往有“四两拔千斤”的功效.

证法6(利用lnx≤x－1及cosx的有界性放缩)因为lnx≤x－1,所以xlnx＋1≤x(x－1)＋1＝x2－x＋1,当x＝1时,等号成立.

又因为cosx≥－1,所以ex＋cosx≥ex－1,当x＝(2k＋1)π,k∈N 时,等号成立.故只需证x2－x＋1＜ex－1(x≥1),即证ex－x2＋x－2＞0.

设g(x)＝ex－x2＋x－2(x≥1),则

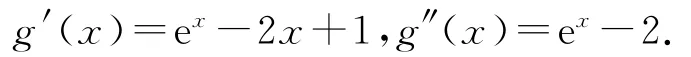
因为x≥1,故g″(x)＞0,于是g′(x)在[1,＋∞)上单调递增,从而可得g′(x)≥g′(1)＝e－1＞0,所以g(x)在[1,＋∞)上单调递增,可得g(x)≥g(1)＝e－1＋1－2＝e－2＞0,所以ex－x2＋x－2＞0.

综上,当a＜0时,f(x)＜ex＋cosx.

综上,当a＜0时,f(x)＜ex＋cosx.

证法6 与证法7 都利用了lnx≤x－1 及cosx的有界性进行放缩,是证法2与证法3的结合,证法巧妙、快捷、简便,简化了证明过程.

2.3 利用泰勒展开式

证法8由泰勒展开式可知

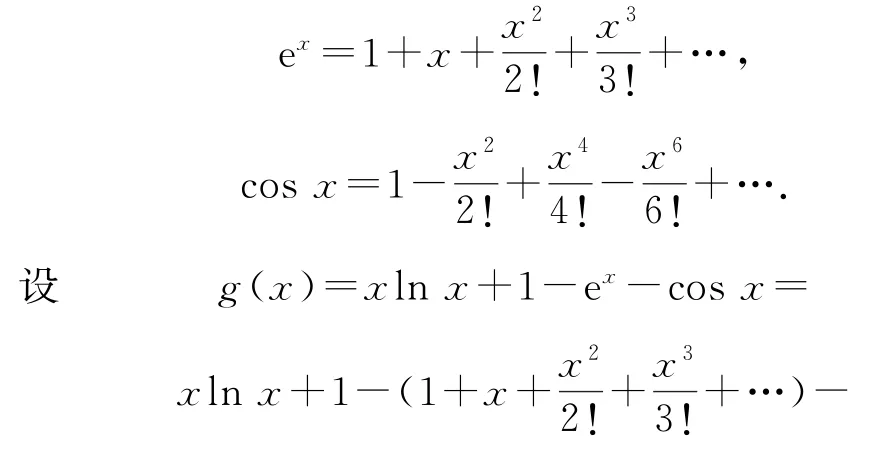
于是h′(x)在[1,＋∞)上单调递减,可得

从而h(x)在[1,＋∞)上单调递减,故

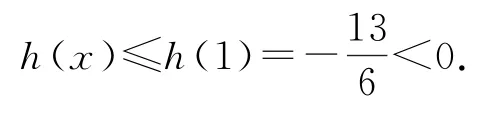
所以g(x)＜0,即xlnx＋1＜ex＋cosx.

综上,当a＜0时,f(x)＜ex＋cosx.

泰勒展开式不在高中学习范围内,学生不需要掌握,但是近年来,高考的命题者通过挖掘高等数学中的一些素材来命制高考试题,此类试题也逐渐引起教师的关注.但这并不意味着要将过多的高等数学知识放到中学里来,加重中学的负担,教师需要站在高观点的角度看待问题,找到问题的本质内涵,弄清命题人的命题方向,更好地指导中学的数学教学.

3 小结

从上述的各种证法,可以看出在证明函数不等式的题型中,不管问题如何变化,多数还是把函数不等式的证明转化为研究函数的单调性或求最值.常见的证明方法有构造函数证明;利用函数不等式模型ex≥x＋1,lnx≤x－1(x＞0)进行放缩;借助三角函数的有界性进行放缩等.因此,在复习中必须清楚单调性是函数的核心性质,要深化对函数单调性的认识,注重导数法在函数单调性中的应用.另外,要善于总结,将函数与导数试题分门别类,并归纳出常用的解法,通过解题训练提炼函数问题的数学思想,重点运用转化与化归、数形结合、分类讨论等思想方法处理函数与导数问题.

(完)