导数在实际生活中的应用问题
2022-03-14于苗苗
于苗苗
(山东省平度第一中学)
导数在实际生活中的应用问题一直是高考的热点之一.此类问题通常以实际生活应用为命题背景,进而结合数学知识合理构建相应的数学模型,借助题目条件适当选定相应的变量,寻找各变量之间的关系,并构建对应的数学关系,特别是相应的函数关系,结合函数的求导,利用导数法来转化与解决对应的实际应用问题时,要从数学角度给出合理的、最佳的决策方案.
1 生活判断方面的应用问题
例1随着城市的不断发展,交通状况越来越受到大家的普遍关注.根据某城市有关的数据统计,从每天上午7时到10时,车辆通过该市某一路段的用时y(分钟)与车辆进入该路段的时刻t之间的关系可近似地用如下函数来表示:y=-+36t-,则在每天上午7时到10时这段时间内,通过该路段用时最多的时刻是( ).
A.6时 B.7时 C.8时 D.9时
分析对生活中实际问题所对应的函数解析式进行合理求导,并确定导函数的零点,结合实际问题判断其单调性、极值,是求解相应的最值问题的策略.
解令y′=-t+36=0,即t2+4t-96=0,解得t=8或-12(舍),当7<t<8时,y′>0;当8<t<10时,y′<0,所以当t=8时,函数有极大值,也是最大值,故选C.

涉及生活判断方面的应用问题,求解关键是合理建立数学模型,正确求导,确定对应的单调性、极值与最值,并结合生活实际合理判断与应用.
2 技巧工具方面的应用问题
例2已知x,y∈R*,且满足+2y=3,则的最大值为________.
分析根据条件中代数式的定值确定参数x的取值范围,进而利用消参法把转化为含有参数x的函数f(x),结合函数f(x)的导函数确定f(x)的最大值,从而确定的最大值.


在确定一些代数式的最值问题时,特别是多元代数式、分式、根式等问题,经常借助导数法来进行求解,从而达到合理快捷破解问题的目的.
3 知识融合方面的应用问题
例3如图1所示,圆形纸片的圆心为O,半径为5cm,该纸片上等边△ABC的中心为O.D,E,F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D,E,F重合,得到三棱锥.当△ABC的边长变长时,所得三棱锥体积(单位:cm3)的最大值为______.

图1
分析根据平面几何的知识,设出相应的参数,进而推导出三棱锥体积V的解析式,构造函数,结合导数法的处理来确定相应的最值,进而确定所得三棱锥体积的最大值.


图2


本题巧妙把棱柱和棱锥的知识、函数的概念、导数的应用等巧妙融合,同时结合数学建模、空间想象等能力,有效整合知识,拓展数学应用.
4 规划决策方面的应用问题
例4海南省为了进一步实施与推进国务院“关于推进海南国际旅游岛建设意见”,决定适当引入民间资本参与全面建设.假设某民营企业承包经营某旅游景点的门票成本价为30元,同时每卖出一张门票需向旅游主管部门上交a元(a为常数,2≤a≤5,且a不计入成本价)的管理费用,经物价部门核定门票最低不低于35元,最高不超过41元.根据市场调查,设每张门票的售价为x元,门票日销售量与ex(其中e=2.71828…)成反比例,且已知若门票价格定为40元/张时,日销售门票500张.
(1)求该民营企业承包经营该旅游景点的日利润P(x)元与每张门票的售价x元之间的函数关系式;
(2)试问当每张门票的售价为多少元时,该旅游景点的日利润P(x)最大,并求出日利润P(x)的最大值.
分析(1)先表示出门票的日销售量y与门票售价x之间的函数关系式,再由已知条件计算参数k的值,进而推导函数P(x)与x之间的函数关系式,要注意确定对应的定义域;(2)通过对函数P(x)求导,利用导数求其最值.
解(1)根据题意,门票的日销售量与ex(其中e=2.71828…)成反比例,可设门票的日销售量y与每张门票的售价x之间的函数关系式为y=(k∈R,k≠0,35≤x≤41),又因为门票价格定为40元/张时,日销售门票为500 张,则有500=,解得k=500×e40,则知y==500×e40-x.那么该民营企业承包经营该旅游景点的日利润P(x)与每张门票的售价x的函数关系式为

(2)由(1)知P(x)=500(x-30-a)×e40-x(2≤a≤5,35≤x≤41),则有
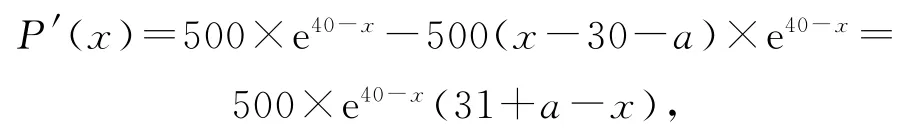
由P′(x)=0,可得x=31+a,则知此时旅游景点的日利润P(x)最大,且P(x)的最大值为500(31+a-30-a)×e40-(31+a)=500×e9-a.

本题是实际问题通过建立函数关系式,利用指数函数的图像与性质以及导数来求解相关的最值问题.关键是正确建立函数关系式,确定参数的取值范围.
在实际应用问题中,对于一些求解有关最优化的实际应用问题,如利润最大、费用最省、路程最短、用时最少、效率最高等问题时,往往需要借助函数的导数这一工具,从数学角度逐步解决实际问题,有效建模,合理解决,提升数学能力,培养数学核心素养.
(完)
