基于ARIMA模型对中国GDP分析和预测

2022-03-14汪衍上海大学悉尼工商学院

品牌研究 2022年4期

文/汪衍（上海大学悉尼工商学院）

一、引言

（一）研究意义

国内生产总值(GDP)可以用来反映一国在单位时间内所有经济活动的经济成果，是反映一国经济总量和发展情况的一个重要衡量指标，也是一国政府制定货币政策，财政政策所参考的重要经济指标。当国内生产总值呈正向增长时，可能说明该国经济正处于增长趋势，或一国目前采取积极、扩张性财政政策与货币政策；反之，则该国经济可能处于衰退期，或出现结构性调整。此外国内生产总值与失业率、经济增长率、通货膨胀率等宏观经济指标有强烈的相关性，因此研究国内生产总值的变动情况，可以很好地反映中国经济的发展情况，为制定未来的宏观经济政策提供很好的理论依据。

目前国内外学者研究国内生产总值的变动情况主要通过时间序列模型，从统计学角度来进行计量分析。时间序列尤其适用于短期经济运行分析，可以较好地对未来短期内货币政策、财政政策的制定提供理论参考。目前学者一般研究国内生产总值的计量模型包括：以研究平稳序列的自回归移动平均(autoregressive moving average model,ARMA)模型和研究非平稳序列的求和自回归移动平均(autoregressive integrated moving average model , ARIMA)模型为代表的时间序列模型。

本文采取计量经济模型中的ARIMA模型研究我国国内生产总值的变动规律，并对2022年我国国内生产总值进行预测，进而得出一些有建设性的结论及建议。

（二）研究内容

本文使用1992年1季度至2021年4季度的国内生产总值（现价）季度数据，通过对数化调整、二阶差分以及季节性调整，消除原始数据所存在的异方差、趋势性、季节性等问题，随后对数据构建ARIMA模型，并根据AIC信息准则选择其中拟合结果相对较好的一个模型，即ARIMA（3,1,2）模型，对2022年全年国内生产总值进行预测。结果显示，2022年我国国内生产总值仍将保持平稳较快速率增长，预计2022年我国国内生产总值将达1227418.3亿元，较2021年同比增长7.32%。

二、相关文献评述

目前在国内外有大量的学者通过ARIMA等模型对GDP、CPI等宏观指标进行了大量的研究：

Hasan Yasien Touama(2014)通过ARIMA模型和Holt线性趋势模型研究约旦2003-2013年国内生产总值的变动情况，分析预测约旦GDP在2014年后短期内会得到提升，同时约旦GDP的预测值在统计学上存在显著性性差异。[1]李守丽 (2013)通过研究郑州1981年-2010年GDP数据，以ARIMA（1,2,1）模型对郑州2011和2022年GDP进行预测，预测结果的相对误差小于3%，模型有较强的现实意义。[2]陈瑶 (2015)通过ARIMA模型研究我国2000年到2014年一季度的GDP数据，并对2014年后三季度GDP进行预测，预测模型较为合理，有较高的理论价值。[3]杨探 (2018)通过ARIMA模型，分析1996年到2012年我国城镇居民人均可支配收入数据，并得出了一定的分析与预测结果，并给出了相关建议。[4]

本文在以上研究成果的基础上，对我国国内生产总值（GDP）的波动做进一步的探索分析，建立模型，并通过预测来检验模型的准确性。

三、数据与实证分析

（一）数据来源

本文选取1992年1季度至2021年4季度的国内生产总值（现价）季度数据。数据来源于国家统计局。首先使用1992年1季度至2021年4季度的季度数据拟合了预测模型，并得到了2022年全年的国内生产总值（现价）预测值。在模型结构和预测误差这两方面都取得了较好的结果。

（二）平稳性检验

通过观测1992-2021年中国国内生产总值（现价）时序图（如图1），发现我国GDP从1992年至2007年增长速度较为平缓，而从2008年以后增速明显加快，我国GDP进入快速增长阶段，同时从图中也可以看出GDP增长有明显的季节性趋势。从总的趋势来看GDP增长是呈现指数增长的趋势，说明序列具有非平稳性，为非平稳时间序列，因此需将原始数据平稳化后才可构建ARIMA模型。

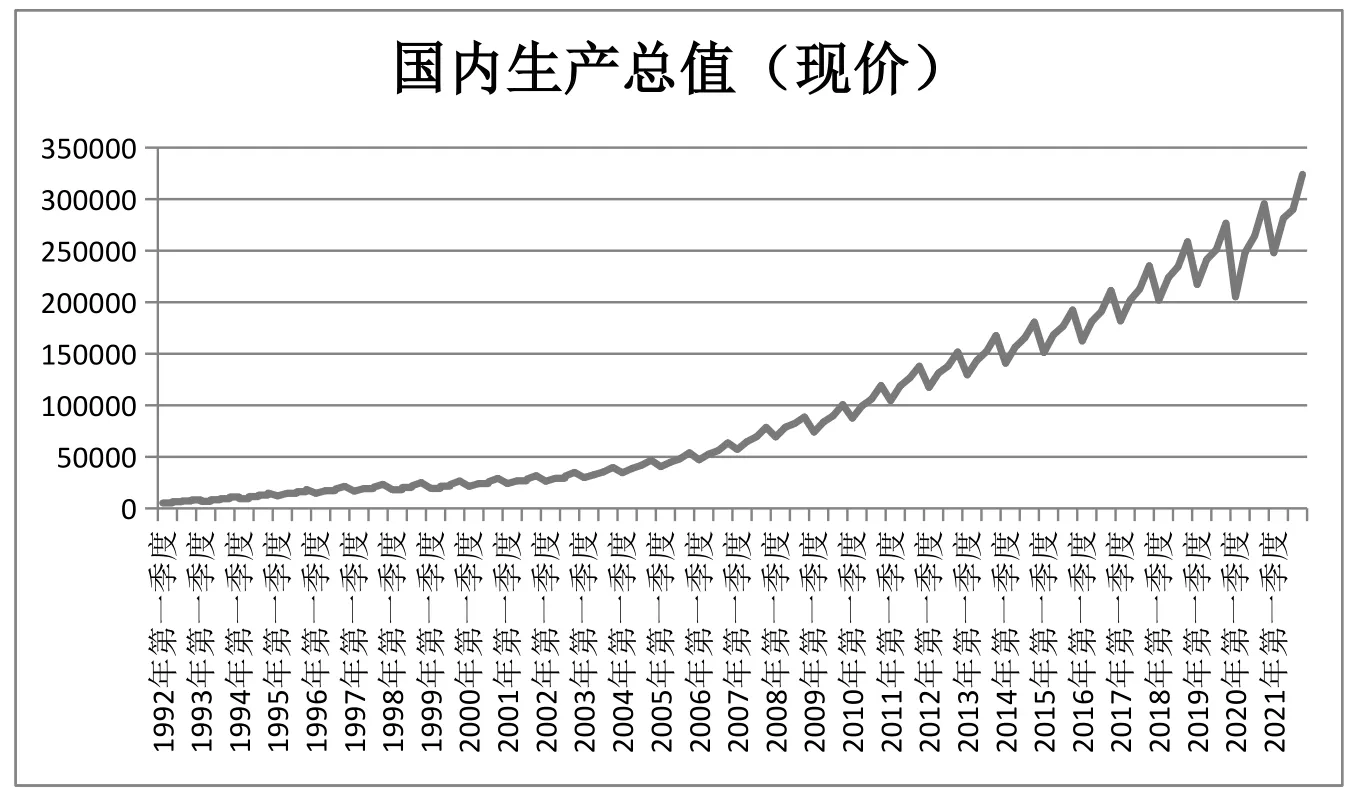
图1 1992-2021年中国国内生产总值（现价）时序图

首先对数据进行对数化处理（对数化序列为lgdp），观察发现序列仍然不平稳，有明显的增长趋势，即对数化后序列仍然是非平稳序列。

接着为了消除序列的不平稳，对其进行一阶差分（一阶差分后序列为dgdp），并通过滞后期为20的ADF检验，发现P值为0.1392，接受原假设，即一阶差分后序列仍然不是平稳的时间序列，存在季节性，需对数据进行进一步处理；然后对一阶差分后数据进行季节性调整，进行4阶差分（季节性差分后序列为sdgdp），通过ADF检验得到P值显著小于0.01，拒绝单位根假设，即此时序列为白噪声序列，sdgdp为平稳序列，此时可以建立ARIMA模型（表1）。

表1 ADF检验结果

（三）模型建立及检验

由于本文数据经过一阶季节差分，季节性基本消除，故D=1。所以选用ARIMA(p,1,q)模型,同时为了避免模型过拟合和使模型较为准确，通过比较各ARIMA模型的AIC信息准则，选择ARIMA（3,1,2）模型作为我们最终的模型。ARIMA（3,1,2）模型拟合结果和统计量如表2、3所示。

表2 各模型的AIC值

构建完时间序列模型后，对ARIMA（3,1,2）残差序列进行检验，jung-Box检验结果显示p值显著大于5%，接受原假设，即残差序列为白噪声序列，ARIMA（3,1,2）模型比较合理，其残差序列不含有信息，即模型显著有效。

（四）模型预测

通过上述构建的ARIMA（3,1,2）模型，对2022年国内生产总值进行预测，并与2021年数据进行对比，结果如表4所示。

表4 2022各季度预期值与上年同期比较（单位:万元）

数据显示，2022年全年四季度较上年同期比较分别增长约6.54%，5.97%，7.80%，8.67%；全年预期国内生产总值将达1227418.3亿元，较2021年同比增长约7.32%，即2022年我国国内生产总值仍处于增长趋势，增速保持平稳较快水平。

表3 ARIMA（3,1,2）模型的各统计量

四、结语

本文通过研究1992-2021年我国GDP季度数据构建ARIMA（3,1,2）模型发现，预计2022年我国国内生产总值仍将保持平稳较快增速发展。同时根据本文分析，国内生产总值受到许多因素不同程度的影响，加上自身具有季节性，因此需采取积极的货币政策和财政政策，才能保证国内生产总值的平稳增长。可采取的货币政策和财政政策包括积极做好金融支持实体经济、支持就业创业工作，深入开展金融精准扶贫以及继续加强产业转型升级的金融支持，充分灵活利用政府债券和各类支出工具，发行特别国债和地方专项债券，加快公共财政支出增速，适度扩大赤字等。