公立医院PPP项目风险分担博弈研究

文/余洋（沈阳建筑大学 管理学院）

一、引言

随着我国近些年的快速发展，当前医疗基础设施越发不能满足人民群众对于公共医疗服务的要求，而面对此难题，地方政府难以支撑医疗项目的建设费用，导致出现了医疗资源分配不均、医疗服务效率低等问题。为此，国务院不断增加医疗行业的财政支出比例和发布一系列政策鼓励社会资本积极参与医疗项目建设。引入社会资本参与医疗项目不仅能解决地方财政投入的不足，也能发挥各自优势，弥补公共部门和私人部门在项目建设运营方面的不足。对于解决经济欠发达地区医疗窘境具有极大的意义。

公立医院PPP项目是指公立医院、社会资本方、医院主要参与三方通过合作共同完成从医院建设到运营等全生命周期服务的项目，面对医疗项目建设技术复杂、专业性强、回收周期长等比一般项目更多更复杂的潜在风险，合理的风险分担机制能够使风险在主要参与方之间合理分担，成为影响医疗项目成败的关键因素。

国内外学者研究PPP风险分担主要有定性和定量分析两种：定性分析有EL-Sayegh（2008）使用调查问卷的方法确定参与主体风险分担比例[1]；张曾莲（2017）等通过浏览大量文献并对其进行打分得到分担比例[2]；定量分析有王雪青等（2007）基于主要参与方风险偏好系数的不同，使用博弈论的研究方法，确定风险最适合承担方[3]；李林等（2013）利用讨价还价模型确定PPP项目的风险分配[4]；宿辉（2021）等通过问卷调查得到相关博弈影响因子并建立动态博弈模型进行分担[5]。

基于上述认识，本文以公立医院PPP项目为研究对象，通过初次分担博弈分析出独自承担风险和共同承担风险，并利用讨价还价模型动态博弈分析共担风险的比例，为公立医院PPP项目顺利建设运营提供理论基础。

二、初步分担博弈模型构建

相比定性分析方法，博弈论分析更加合理均衡，且公立医院PPP项目参与方众多，更加注重共同合作，社会资本和政府方、医院方都因自身利益而满足“理性人”假设，因此本文采用博弈论方法对风险分担进行研究。

（一）模型要素分析

（1）参与方：公立医院PPP项目风险主要由政府、社会资本、公立医院三方承担，使用j=1，2,3进行表示。

（2）策略：指参与方的行为决策，在本文分析中，参与三方均有“承担”“不承担”两种处理方式。

（3）效用：指参与方通过博弈得到的利益或者损失。本文采用满意度表示效用水平，参与方满意度为正数即为风险分担收益高于成本。

（4）信息：指各个参与方了解的其他各方行动收益、损失、策略等相关信息。

（二）基本假设

（1）假设1：各参与方都是“理性人”，共同目的均为项目顺利开展。

（2）假设2：所有风险均为独立的，在博弈过程中不互相影响。

（3）假设3：各个参与方对风险的分担和收益成正比。

（三）初次分担模型的构建

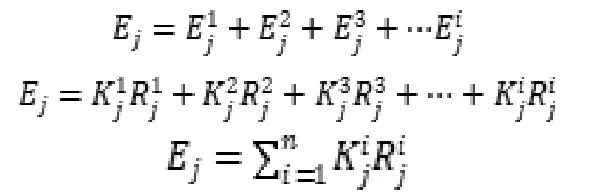
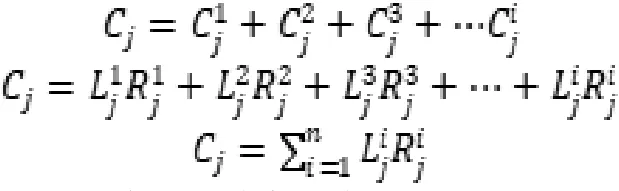
由前文的满意度定义可得：

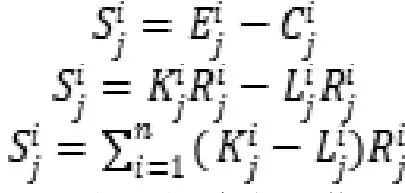
由上述定义构建完全信息静态博弈模型，公立医院PPP项目第i个风险博弈结果如表1所示。

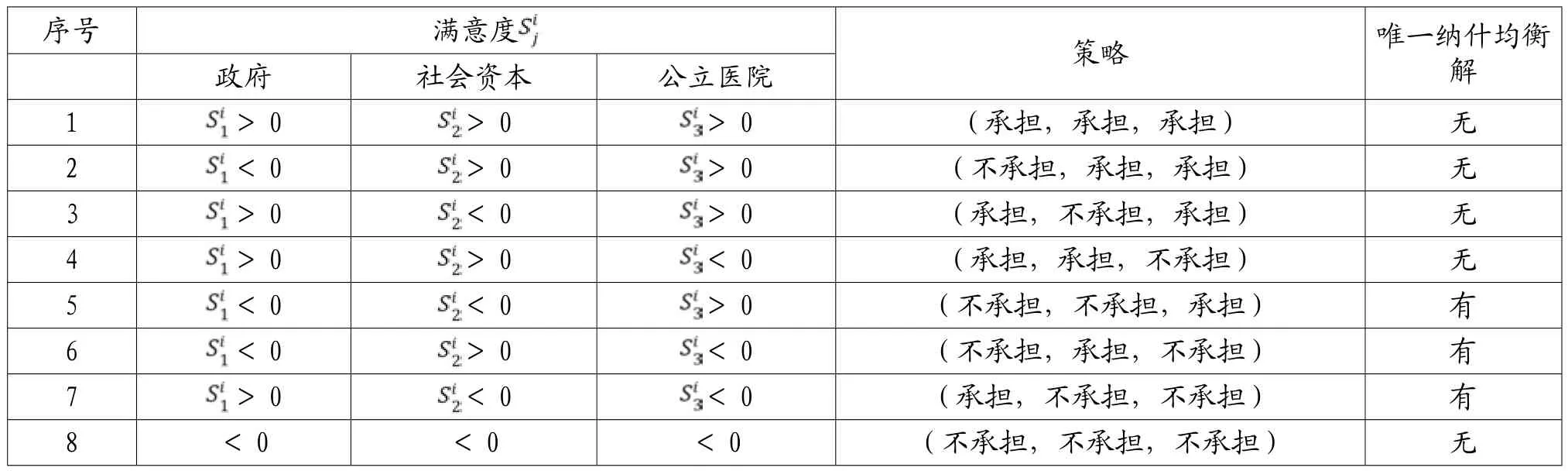
表1 项目风险初步分担博弈结果

分析可得以下结论：

（1）出现情况1,2,3,4时，博弈模型不存在唯一纳什均衡解，代表该风险分担需要进一步博弈，在后文进行讨论。

（2）出现情况5,6,7时，博弈模型存在唯一纳什均衡解，该风险由一方独自承担。出现情况5时，政府方和社会资本方满意度均为负，而公立医院方满意度为正，代表公立医院承担该风险会带来收益，而政府方和社会资本方承担风险则会带来损失，因此由公立医院承担该风险；出现情况6时，政府方和公立医院方满意度为负，社会资本方满意度为正，因此由社会资本方承担该风险；出现情况7时，社会资本方和公立医院方满意度为负，政府方满意度为正，因此由政府方承担该风险。

（3）出现情况8时，博弈模型不存在唯一纳什均衡解，代表政府方、社会资本方、公立医院方任意一方承担该风险时候都会带来损失，则应该将该风险合理转移，由公立医院PPP项目其他参与方进行承担。

三、风险再分担博弈分析

对于风险初次分担存在唯一纳什均衡解的情况，需要进一步博弈谈判出合理的分险分担机制。以上文情况4政府方和社会资本方共用承担某风险为例，对于某一风险因素，政府方首先提出方案己方承担k份额（0＜k＜1）的该风险，如果社会资本方同意政府方提出的该方案，则谈判结束达成协议，如果社会资本方不同意，则进入下一轮谈判。第二轮社会资本方提出风险分担方案，如果政府方同意该方案，则谈判结束，如果政府方不同意，则下一轮政府方出价，一直循环下去，直至达成双方都满意的风险分担份额，博弈结束。

（一）基本假设

（1）假设一：双方均是理性的，双方均不想要谈判破裂，不想拖延时间，均想要尽快达成协议。

（2）假设二：各个风险互相独立，没有关联。

（3）假设三：政府方和社会资本方掌握的信息是不同等的，即在谈判中，一方对另一方行动的得益损失并不能完全了解。

（4）假设四：政府方对于某风险承担比例为k，则社会资本方承担的风险份额为1-k，双方在谈判中对参数k进行讨价还价博弈。

（二）再分担博弈参数设置

（1）在公立医院PPP项目风险分担博弈谈判过程中，谈判拖延下去参与双方都会有时间和机会上一定的损失，因此，在谈判过程中需要考虑谈判损耗系数，而根据实际情况，政府方的谈判损耗系数＜社会资本方的谈判损耗系数。

（2）政府方在每个回合过程中想要向社会资本方转移的风险份额α，假设每个回合α一致（0＜α＜1）。

（3）社会资本方知道政府部门会采取强势地位转移风险的概率为。

（三）再分担博弈模型的构建

根据实际情况，政府方往往在现实中掌握更多政策资源，在风险分担博弈过程中社会资本方往往不如政府方强势，因此，在讨价还价博弈中，由政府方首先出价。第一回合：假设政府方采取强势地位威胁私人部门的概率为，政府方首先提出自己对待某风险愿意承担的比例，则社会资本方承担的比例为1-，同时，政府方在此回合想要向社会资本方转移风险的份额为，因此可得：

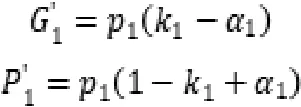
政府方也有可能在第一回合中不威胁社会资本方，不威胁的概率为1-，在此情况下双方分别承担风险为：

由上述可推导，政府方和社会资本方在第一回合中承担的风险期望为：

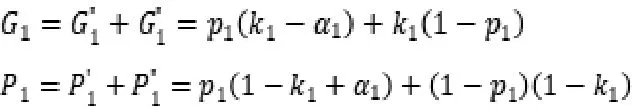
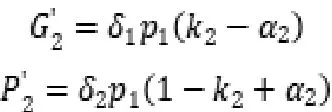
同样，在政府方不威胁社会资本方的情况下，在此情况下双方分别承担风险为：

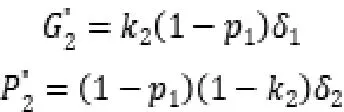
由上述可推导，政府方和社会资本方在第二回合中承担的风险期望为：

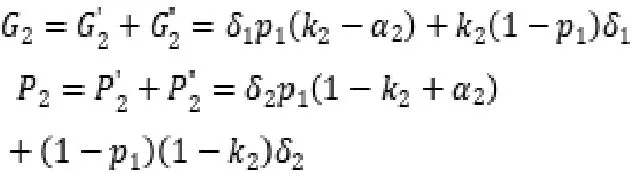
同理，政府方和社会资本方在第三回合中承担的风险期望为：

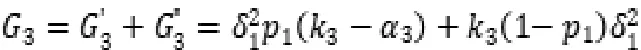
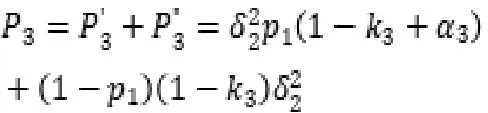
博弈一直循环下去，直至双方意见一致，顺利达成协议。

（四）模型求解

根据海萨尼转换理论，在任意回合设置逆推点所得结果都是一致的，在此首先设置第三回合开始逆推，若第二回合社会资本方提出的方案使政府方风险期望＞，则政府方作为“理性人”定会拒绝第二回合的方案，博弈直接进入第三回合。而谈判拖延下去会造成双方损失，因此，社会资本方第二回合提出的方案应该是满足自身利益的前提下，使不大于，从而避免自身更多的损失。

即：

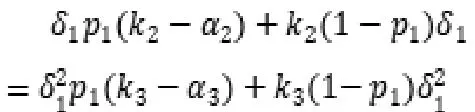
推导可得：

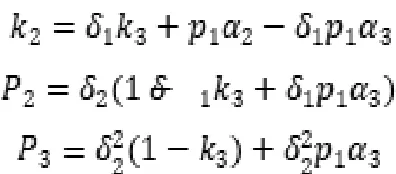
即社会资本方在第二回合承担的风险小于第三回合，则双方均不愿意将谈判拖延至第三回合。

同理，在第一回合开始逆推，政府方首先提出方案且同样不想进入下一回合造成损耗，因此需满足。

即：

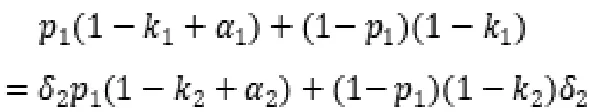
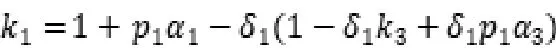
则可推导出双方承担风险比例的结果。

政府方：

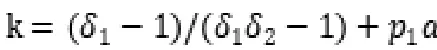
社会资本方：

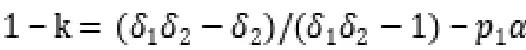
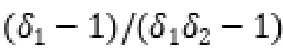
四、结论

作为人民群众生命健康的保障，医疗项目的建设在城市发展中具有十分重大的意义，而随着国家政策的推进在医疗项目建设中引入PPP模式将成为首要选择。在公立医院PPP项目风险分担过程中，各参与方要在地位平等的基础上进行合作，确保按照风险分担的基本原则，即风险由最有能力控制风险的一方承担，面对特殊情况，也可以将风险转移给其他参与者从而降低损失。最后，需要注意避免因信息不对称而引起的循环谈判导致的谈判损耗。