枕头坝—沙坪二级河段流量延时时间分析

郭 爽，龙 岩，王孝群，马芳平

（1.河北工程大学水利水电学院，河北 邯郸 056038；2.河北工程大学河北省智慧水利重点实验室，河北 邯郸 056038；3.国能大渡河流域水电开发有限公司，四川 成都 610000）

1 研究区域

沙坪二级水电站是大渡河规划的22个梯级水电站中的第20级，是沙坪梯级水电站的第二级，具体位置如图1所示，上邻沙坪一级水电站，下接龚嘴水电站。沙坪电站总库容2 084 万m³，死水位550.0 m，正常蓄水位554.0 m，可调库容585 万m³。坝前水位对于入库流量变化十分敏感。电站布置6台灯泡贯流式水轮发电机组，电站单机容量58 MW，总装机容量348 MW。枕头坝与沙坪电站属于上下游梯级，水力联系十分紧密，且由于两站之间没有区间汇流，枕头坝的出库流量几乎可以认为是沙坪电站的入库流量[1，2]。

图1 枕头坝一级至沙坪二级河道

2 一维河道模型建立

2.1 模型简介

HEC-RAS 是由美国陆军工程兵团水电工程中心研发的河道水面线计算软件，可以执行多种涉水结构的水面线分析计算。在河道水力分析模型中，一维非恒定流模型通过求解一维圣维南方程组计算水面线[3，4]。

软件水力分析模块包括一维恒定流模拟、一维非恒定流计算、移动边界泥沙沉积物的迁移模拟及水质分析4个模块[5]。本文研究计算主要采用HECRAS 的一维非恒定流计算模块，原理主要依据连续方程及动量方程[6]，具体方程如下：

连续性方程为：

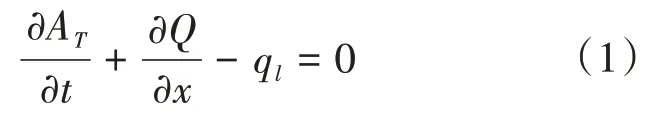
动量方程为：

式中：A为过水断面面积（m2）；t为时间（s）；Q为流量（m3/s）；x为河道计算长度（m）；q为旁侧入流（m3/s）。

Sf可由下式表示：

式中：Sf为摩阻比降；nc为河道糙率；R为水力半径（m）；其余变量含义同上。

离散方程采用隐式有限差分格式如下。

连续性方程为：

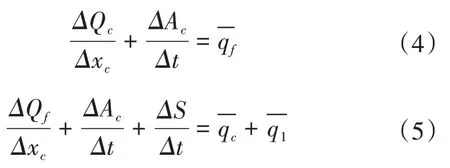
动量方程为：

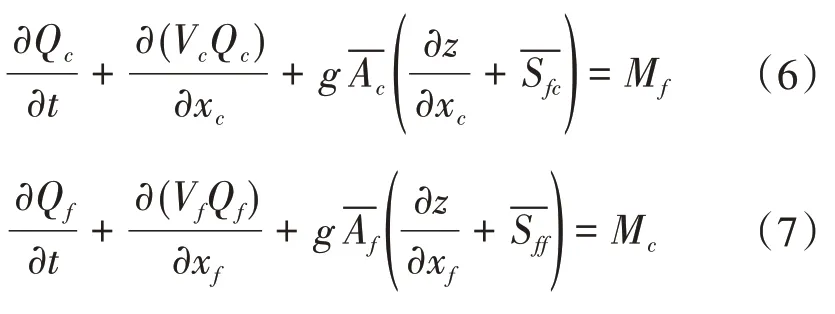
离散过程中采用时间和空间离散，均为一阶离散。

在糙率公式分析中，HEC-RAS软件采用最为常见的谢才公式与曼宁公式：

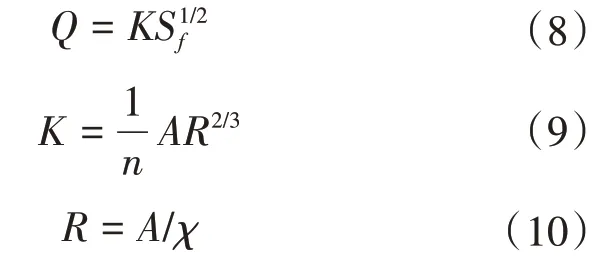
式中：n为糙率；χ为湿周（m）；其余变量含义同上。

2.2 数据采集

本次模型建立主要需要以下2 个方面的基本资料：边界或沿线控制断面的水情（水位、流量）资料和河道沿线的断面资料。水情数据来源于枕头坝一级水电站和沙坪二级水电站的历年实测数据，包括2019和2020年边界或沿线控制断面的水情资料，由于沙坪二级电站上游缺乏流量监测设备，所以实测数据缺乏沙坪二级电站入库流量数据；河道沿线的断面资料来源于枕头坝—沙坪二级区间河道的实测大断面数据，断面资料包括：枕头坝—沙坪区间共27 个断面，其中断面19 为沙坪二级电站的入库断面，缺少枕头坝一级下游6 km 范围内的断面资料。断面资料的缺失将会给一维水动力数值模拟的精度造成一定程度影响。为此，借助断面4 和枕头坝坝上断面虚拟3 个断面，并使用优化算法进行参数自动率定，用于水动力模型构建。各断面的详细位置，见表1。

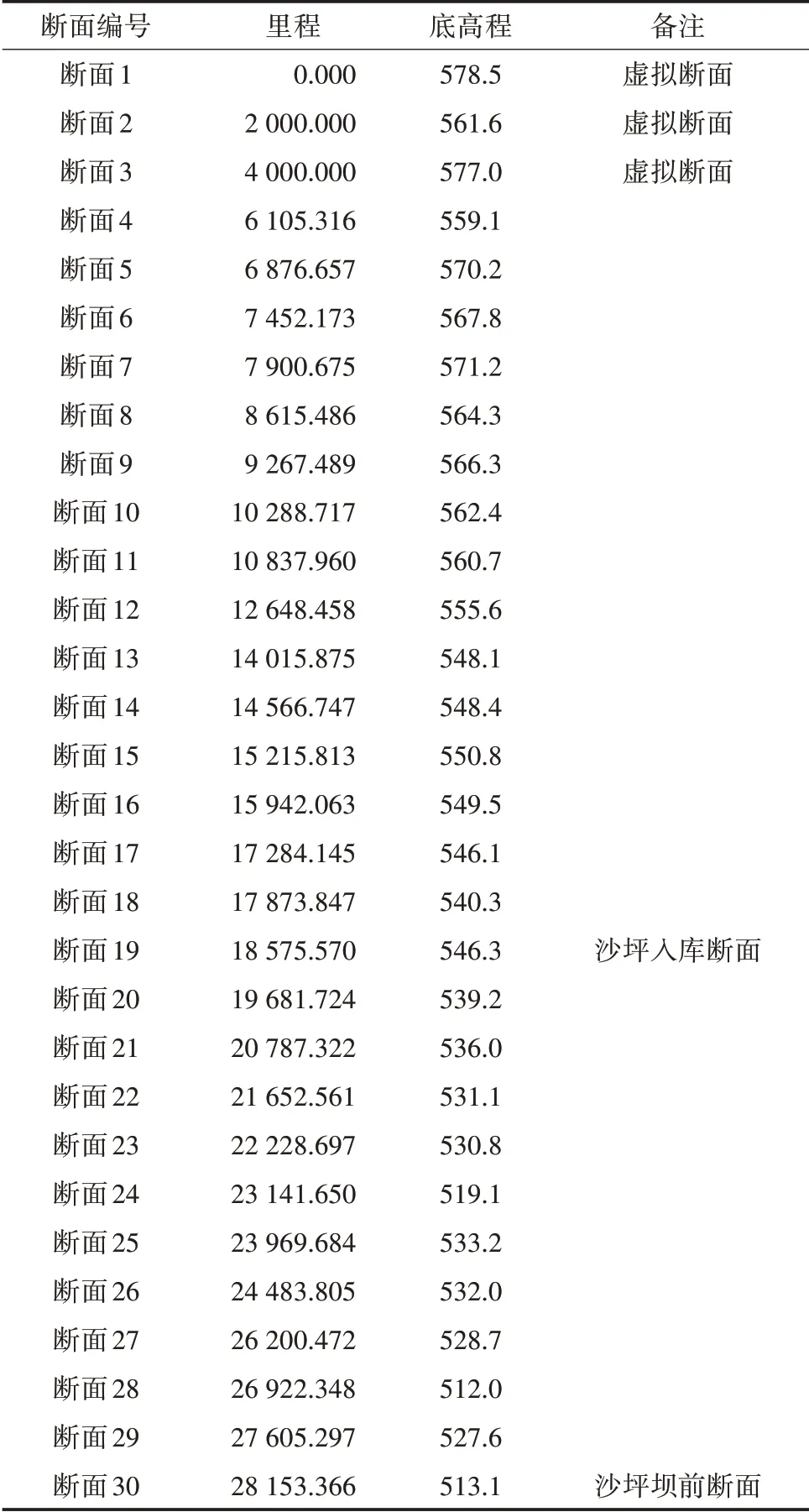
表1 研究河段各断面详细位置 m

2.3 河道糙率率定

在一维河流水动力模拟计算中，影响水位计算结果的因素有很多，如河道糙率、过水断面面积、水流流量、流速等，其中糙率对河道输水损失至关重要。作为本研究多种输入参数中的唯一可变条件，本研究将通过改变糙率来调整模型精度。

由于实测资料缺少枕头坝下游6 km 范围内的大断面资料，采用虚拟断面来进行模拟研究。虚拟断面的方法容易造成较大的数值模拟误差，所以以人工试错法改变河道糙率后来进行水动力模拟：选取汛期和非汛期各具代表性的1个月进行水动力仿真模拟，并分析模拟误差，以此来确定虚拟断面的可行性。

通过对2019 年全年数据进行梳理可知，枕头坝出库流量范围为197～4 750 m3/s，如图2所示。

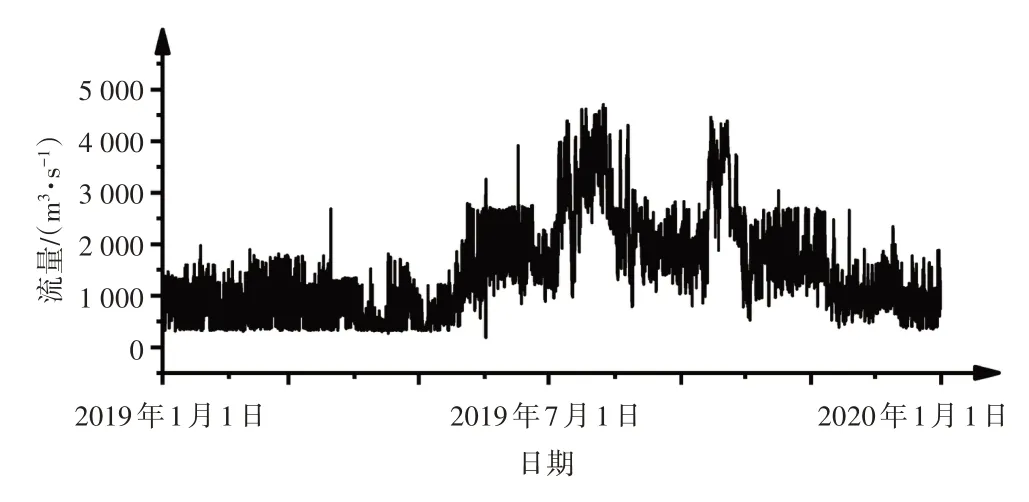
图2 2019年全年枕头坝出库流量过程

各月平均流量分别为869.91、880.89、843.46、624.39、963.51、1 894.33、3 013.04、2 049.47、2 547.23、1 660.02、1 143.27 和976.99 m3/s，如图3 所示。由于6、7、8、9、10 月流量较大，均大于1 600 m3/s，因此我们判断研究流域汛期为6—10 月、剩余月份为非汛期。

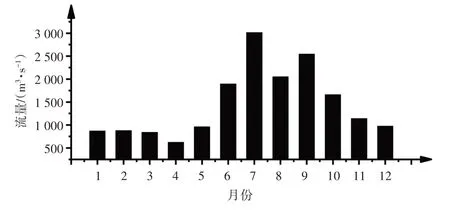
图3 枕头坝2019年各月平均流量

汛期选择2019 年6 月为代表，枕头坝出库流量模拟计算输入输出时间为3 min，沙坪二级上游水位模拟计算输入输出时间为5 min，通过人工试错法改变糙率，其他参数不变，率定得到模拟数据与实际数据拟合程度最高、误差最低情况下对应的糙率为0.049，模拟结果如图4—5所示。

图4 2019年6月枕头坝下游水位过程

图5 2019年6月沙坪出库流量过程

非汛期选择2019年12月为代表，枕头坝出库流量模拟计算输入输出时间为3 min，沙坪二级上游水位模拟计算输入输出时间为5 min，通过人工试错法改变糙率，其他参数不变，率定得到模拟数据与实际数据拟合程度最高、误差最低情况下对应的糙率为0.058，模拟结果如图6—7所示。

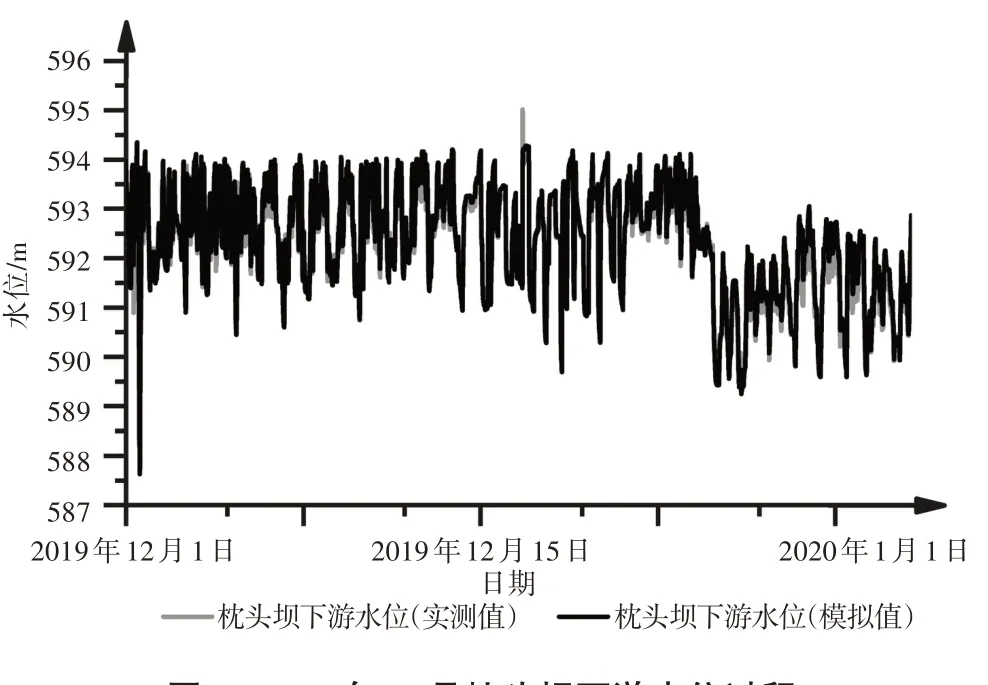
图6 2019年12月枕头坝下游水位过程

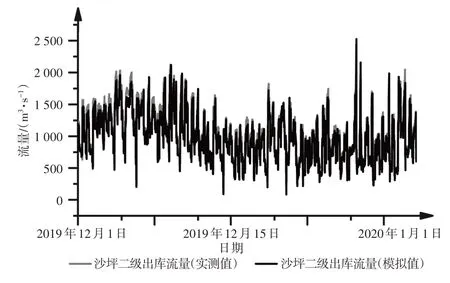
图7 2019年12月沙坪出库流量过程

由上述模拟结果可以看出，枕头坝坝下水位模拟误差较低，沙坪二级出库流量模拟值与实测值一致性较好。经计算得出：枕头坝坝下水位汛期（2019年6月）模拟值与实际值的相关系数为0.972 1、平均模拟误差为0.19 m，非汛期（2019 年12 月）模拟值与实测值的相关系数为0.977 3、平均模拟误差为0.36 m；沙坪二级入库流量汛期平均模拟误差为15%，非汛期平均模拟误差为12%。因此，确定使用虚拟断面模拟的模型精度可以满足水力调控和响应时间计算需求。

确定了水动力模型的可行性之后，利用人工试错法对2019 年全年逐月进行糙率率定，本研究采用相关系数和平均误差来评价数据准确性，其中相关系数R表示2 个变量之间线性相关关系，R越接近1表示模拟值与实测值的吻合程度越高，一般来说R介于0.9～1 可以称为2 组数据高度相关；平均误差η是数列中各项数值与其算术平均数的离差绝对值的算术平均数，数值越小2 组数据偏差越小[7]。2 种方法定义式如下：

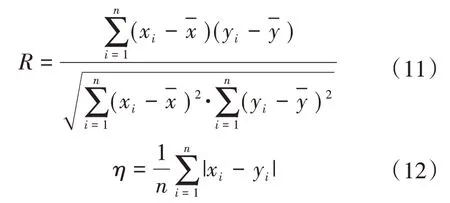
式中：xi为枕头坝下游水位实测值（m）；为实测平均值（m）；yi为枕头坝下游水位模拟值（m）为模拟平均值（m）；n为数据长度。

2019 年各月率定糙率模拟误差，详见表2—3。

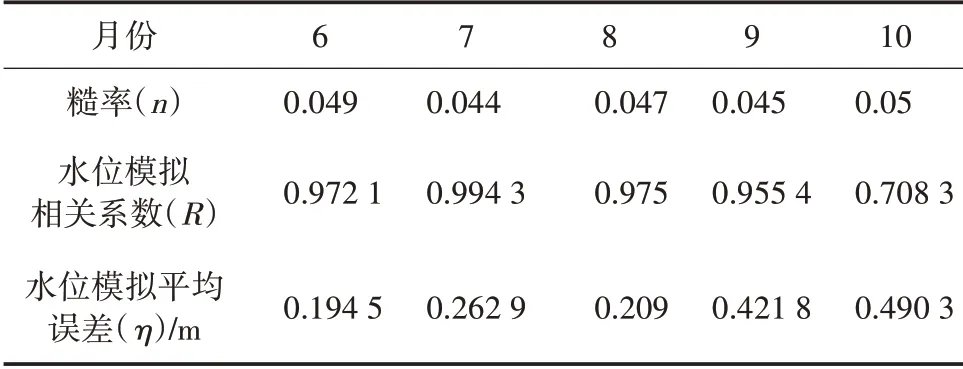
表2 汛期各月率定糙率误差分析

表3 非汛期各月率定糙率误差分析

由表2—3 可知，在2019 年中，5 月枕头坝下游水位模拟值与实测值的拟合程度最高，R为0.994 8；10 月水位模拟值与实测值的拟合程度最低，R为0.708 3；其余月份水位模拟值与实测值拟合程度都较高；分析原因可能为10月为汛期和非汛期的交汇处，该月前后数据量级差距较大，导致R相对较低，但也可以称之为高度相关。2019年5月枕头坝下游水位模拟值与实测值的平均误差最高，η为0.497 6 m；6 月水位模拟值与实测值的平均误差最低，η为0.194 5 m；分析原因可能为6 月数据量级交叉波动较大，但整体数据误差低于0.5 m，也可以满足实际应用要求。

3 延时时间确定

枕头坝与沙坪二级电站属于上下游梯级，水力联系十分紧密，且由于两站之间没有区间汇流，枕头坝的出库流量几乎可以认为是沙坪二级电站的入库流量。然而，还需要注意的是，由于从枕头坝出库到沙坪库尾还有较长的距离，枕头坝出库与沙坪入库之间存在一定的时间延迟，本研究对2019 年枕头坝—沙坪二级的流量数据进行相关性分析，可粗略估计延时时间。事实上，一般认为不同流量的径流速度不同，因此必须将流量分级，分析不同流量级下枕头坝出库流量与沙坪入库流量之间的延迟时间[8]。

通过对2019 年全年数据进行梳理可知，枕头坝出库流量范围主要集中在1 000～4 000 m3/s，因此本研究将枕头坝出库流量分为1 100、1 500、1 900、2 300、2 700、3 100、3 500、3 900 m3/s 8 个量级，分别选取不同量级的枕头坝出库流量数据作为上游边界、对应时间的沙坪二级上游水位作为下游边界进行糙率率定。

例如，2019 年3 月7 日的枕头坝日均出库流量为1 073.14 m3/s，本研究将此数值归属于1 100 m3/s量级，并将此数据作为上游边界、当日沙坪二级上游水位作为下游边界输入模型中进行模拟，初始流速为1 100 m3/s，模拟时间为24 h，计算间隔、水文过程线输出间隔、输出图形间隔、详细输出间隔均为1 min，通过人工试错法改变糙率得到拟合程度最高的枕头坝下游水位过程，拟合结果对应糙率为0.058，对应枕头坝下游实测水位与模拟水位对比过程如图8所示。同理计算出不同量级枕头坝出库流量对应的模型河道糙率并进行误差分析，结果详见表4。

图8 枕头坝下游实测水位与模拟水位对比过程

表4 不同量级出库流量的率定糙率误差分析

由表4可知，在模型中，河道糙率最高值为3 900 m3/s流量量级对应的率定糙率0.042，最低值为1 100 m3/s流量量级对应的率定糙率0.058，糙率随着出库流量的增加而减小，且8 个量级对应的模拟结果与实测值对比的相关系数R均处在极高相关水平，且平均误差均低于0.25 m，因此模型率定结果精度较高，由此可以得出在该研究水动力模型中河道糙率与枕头坝出库流量成负相关关系。

分析实测时间序列x（t）和y（t）之间的互相关关系时，引入互相关函数来进行时间延迟的确定。互相关函数是用来计算2个信号传播路径上的时间延迟的函数。通常使用式（13）来求解互相关函数。

将对应8 个量级的枕头坝出库流量与沙坪二级上游水位输入水动力模型中，计算出沙坪入库断面流量（沙坪二级电站前没有水位监测装置，本模型以第19 断面作为入库流量断面），并与当天对应的枕头坝出库流量使用SPSS 分析软件进行交叉相关性分析，计算枕头坝出库与沙坪入库流量的互相关函数，即可得出水流的延时时间与流量的关系。

例如，选择枕头坝日均出库流量为1 500 m3/s的模型数据进行水动力模拟后，将模型输出结果中的断面19 的24 h 的流量数据导出作为沙坪二级入库流量，绘出2组流量数据对比图，如图9所示。

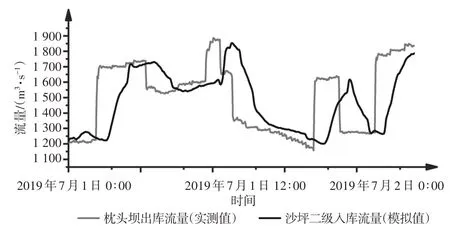
图9 沙坪二级电站入库流量与枕头坝出库流量过程（1 500 m3/s）

将枕头坝出库流量与沙坪二级模拟入库流量进行交叉相关性分析得到互相关系数曲线，同理绘出其他量级枕头坝出库流量与沙坪二级入库流量的互相关系数曲线，如图10—13所示。

图10 入库流量为1 100、1 500 m3/s时互相关性分析

图11 入库流量为1 900、2 300 m3/s时互相关性分析

图12 入库流量为2 700、3 100 m3/s时互相关性分析

图13 入库流量为3 500、3 900 m3/s时互相关性分析

由图10—13 可知，枕头坝出库流量与沙坪二级入库流量相关性很强，8 个量级由低到高所对应的延时时间分别为83、75、61、60、57、55、52、50 min，延时时间随着上游枕头坝出库流量的增大而减小。

4 结论

本文运用河道水力分析模型HEC-RAS 构建了大渡河干流枕头坝—沙坪二级河段的一维水动力模型，介绍了模型软件所用的离散方法和方程求解方法。通过调节输入参数中的唯一可变条件糙率，研究在模型中上游边界流量与糙率的关系，引入互相关函数，借助SPSS 数值分析软件进行互相关分析，分析不同流量级下枕头坝出库流量与沙坪二级入库流量之间的延时时间，得出了以下结论。

（1）在模型中上游边界流量与模型的河道糙率呈负相关关系，模拟精度受实测数据精度影响较大。

（2）在模型中不同流量的径流演进速度不同，流量越大，径流演进的速度越快，符合物理规律，流达时间范围在50～83 min内。

（3）本研究所采用的空间精度数据精度不足，数据高程模型精度越高，模拟越接近于实际情况，并且由于缺乏河段桥梁、涵洞、块状阻水建筑物等的参数，没有将它们导入一维模型中，以上情况导致河道模型无法达到最高水平，有待进一步研究。