东平湖近13 a水位蓄水量变化趋势及突变分析

2022-03-14张耀鑫谭秀翠

海河水利 2022年1期

张耀鑫，谭秀翠

（山东农业大学，山东泰安 271018）

1 研究背景

山东省东平县位于暖温带，属于季风大陆性气候。东平湖区域（东平县境内）总面积627 km2，多年平均年降水量630.6 mm，平均水深2.5 m，平均水位约40.25 m，蓄水总量3 亿m3。东平湖是一个相对复杂的“江河湖库”水文系统，不仅与黄河、大汶河等大型河流相互连接，在黄河、大汶河防汛抗洪中发挥重要作用，也是南水北调东线工程的重要调蓄湖泊，承担着山东省西水东流的任务[1]。东平湖水位、蓄水量动态变动情况，对其防洪、水质、水生动植物生态环境将产生较为重大的影响[2]。

目前，东平湖生态环境越来越恶劣，水质受到不同程度的污染，可利用水资源量减少，地表水资源利用率低，水资源利用效率不高，另外，大汶河流域的污废水以及水土流失严重地影响了东平湖的水质，主要污染指标COD 虽然从1998 年有所下降，但仍高于地表水环境质量Ⅲ类水标准[2]。现代社会经济大幅度发展、过度的水利工程建设和土地开垦、水资源的浪费与污染，使得湖泊水位与蓄水量急剧变化，湖泊河流的生态环境遭到很大破坏，严重威胁着湖泊的生物多样性、生态系统结构的稳定性。

如今，对国内外各大型湖泊的水位、蓄水量变化趋势和突变研究已经成为一个热点，如大量学者研究太湖[3]、鄱阳湖[4]、洞庭湖[5]。而目前对东平湖水位、蓄水量变化的研究还相对较少，但也有了一定的研究基础，如罗辉等[6]对东平湖生态补水进行了初步的研究，贺顺德等[7]研究了东平湖的水量调控调度方案对水位变化的影响程度。对于突变检验在湖泊中的应用，学者们也进行了一系列的研究，如王丹等[8]分析了在近23 a 里气候变化对东平湖水位的影响。吴常雪等[9]利用1973—2018年鄱阳湖枯水期遥感影像数据，采用Mann-Kendall（以下简称M-K）趋势检验法、M-K 突变分析法及Pettitt 突变检验法分析湖泊水体面积变化特征。肖潇等[10]通过M-K 检验、Morlet 小波分析等方法研究长江与洞庭湖汇流河段逐日水位蓄水量数据，分析了汇流河段年内分配、年际变化、变化趋势、突变点及变化周期等一系列水文特征。

因此，本文利用2007—2019 年东平湖水位蓄水量实测数据，研究东平湖水位蓄水量变化趋势并分析其突变过程，找出水位蓄水量突变点，为进一步管理东平湖水资源提供科学依据，对于东平湖水资源保护具有重要意义。

2 数据来源与研究方法

2.1 数据来源

本文采用2007—2019 年东平湖逐日水位与蓄水量资料，数据来源于水利部黄河水利委员会（http：//www.yrcc.gov.cn/）。

2.2 研究方法

2.2.1 线性趋势法

本文采用线性发展趋势法进行趋势分析，其特点是简洁方便、易于理解。以Xi表示样本量为n的某一气候变量、ti表示所对应的时间，建立Xi与ti之间的一元线性回归方程[11]：

这意味着Xi和时间t之间的关系可以用一条合理的直线表示，由于式（1）右边的变量是Xi对应的时间ti，而不是其他变量，因此本文这一研究方法属于时间序列分析范畴。式中，a为回归常数，b为回归系数，Y为因变量，X为自变量，a和b可以用最小二乘法估计得到[11]：

统计参数S计算公式为：

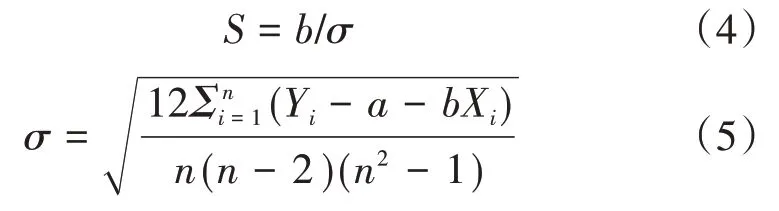
式中：σ为序列的均方差；n为样本容量。

2.2.2 累积距平法

累积距平法是一种可以直观分析判断事物发展趋势不断变化的方法，核心是离散系统数据大于平均值，累积距平值增大，曲线呈现一种上升趋势，反之则呈下降趋势。根据每个要素累积距平值曲线的波动起伏，判断确定事物长期演变趋势及变化趋势已经发生突变的时间[12]。对于水文气象要素x长度为n的序列，其某一时刻t的累计距平cd表示为：

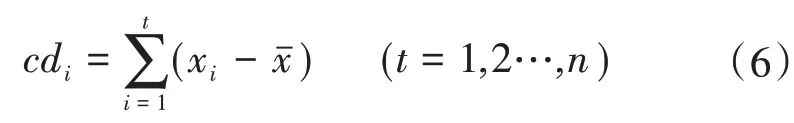
2.2.3 M-K突变检验法

气候系统的变化是一个不稳定、不连续的过程，检验其变化的常用方法之一是M-K 突变检验法。该方法对于元素从一个相对稳定状态转变到另一个相对稳定状态的检验非常有效，且广泛应用于水文、气候、化学、矿物成分检验等方面[13]。M-K突变检验法如下。

对于n个样本的时间序列x，构造一个序列：

其中：

可见，秩序列Sk是第i时刻数值大于j时刻数值个数的累计数，在时间序列的随机独立性假设下，定义了一个统计量[13]：

式中：UK1=0；E(Sk)和var(Sk)分别是Sk的均值和方差。

在x1,x2,…,xn相互独立且有相同连续分布时，它们可由下式算出：

UFk为标准正态分布，即按时间序列x顺序x1,x2,…,xn计算统计量序列，再按时间序列x逆序xn,xn-1,…,x1计算统计量序列，重复上述过程，同时使UBk=-UFk（k=n,n- 1,…,1）、UB1=0，给定显著性水平α、临界值u0.05=±1.96，将UFk和UBk2 个统计量曲线和显著性水平线绘在同一个图上[13]。

3 结果与分析

3.1 变化趋势

分别对东平湖2007—2019 年实测水位资料、实测蓄水量资料进行一元线性回归分析，结果如图1所示。从图1 可以看出，东平湖总体趋势为水位以0.000 2 m/d 下降、蓄水量以0.000 1 亿m3/d 下降，说明近13 a以来东平湖的水位与蓄水量呈现微小的减少趋势。

图1 水位、蓄水量线性趋势

东平湖水位蓄水量拟合图中R2值为0.837 6，相关系数R为0.915 2，表明水位与蓄水量的相关性比较高，如图2所示。

图2 水位与蓄水量线性拟合

3.2 突变分析

为确定水位、蓄水量的突变状态以及开始发生突变的具体年份，本文将利用M-K突变检验法和累积距平法[14]进行东平湖的突变分析，结果如图3—4所示。

图3 2007—2019年东平湖年水位、蓄水量M-K突变检验

3.2.1 水位突变分析

由图3（a）M-K 突变检验曲线可知，第一个阶段：2009年以前，年均水位UF线在0值线上下波动，可以得出在此阶段趋势性不明显，水位变化较小并且变化幅度不稳定；第二个阶段：2009—2014年，UF值一直大于0，可据此得出此阶段水位有一定程度的上升，但因UF线未超过0.05的信度线（+1.96），故上升趋势并不明显；第三个阶段：2014—2019年，UF线在0 值线以下但并未超过0.05 信度线（-1.96），表明东平湖水位在这一阶段呈现不明显下降趋势。

2014年，UF和UB线出现相交，且交点位于0.05信度线之间，由此可以初步判定2014 年是东平湖水位发生显著突变的开始年份。为进一步确定东平湖水位的突变年份，故采用累积距平法进行辅助分析。由图4（a）累积距平曲线可知，曲线发生显著变化的年份为2014年。因此，利用累积距平法也可将2014年作为近13 a 东平湖水位的突变点，结合M-K 突变检验法的判定结果，可进一步确定近13 a 东平湖水位发生突变的时间点为2014年。

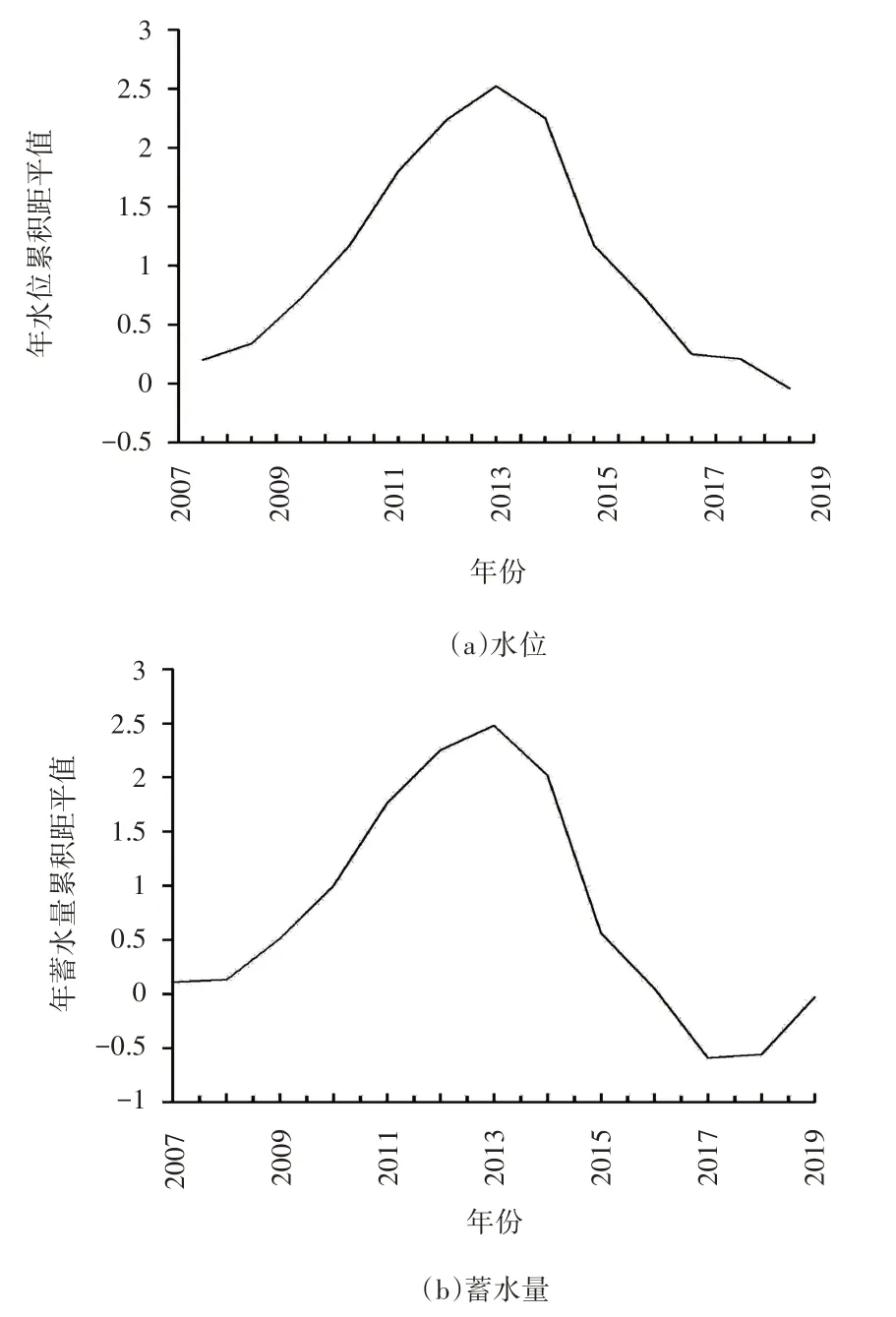
图4 2007—2019年东平湖年水位、蓄水量累积距平曲线

3.2.2 蓄水量突变分析

由图3（b）M-K 突变检验曲线可知，2009 年之前，年均蓄水量UF线在0值线上下起伏，波动较小，表示在此阶段蓄水量变化较小且幅度不稳定，但趋势性并不明显；2009—2014 年，UF值大于0，可得出这个阶段蓄水量有一定程度的上升，但因UF线没有超过0.05 的信度线（+1.96），故上升趋势并不明显；2014—2019 年，UF线在0 值线以下并未超过0.05 信度线（-1.96），表明东平湖蓄水量在这一时期呈现不显著的下降趋势。

2014年，UF和UB线出现相交，且交点位于0.05信度线之间，由此可以初步判定2014 年是东平湖蓄水量发生显著突变的开始年份。为进一步确定东平湖蓄水量的突变年份，仍然采用累积距平法对突变点进行重新检验。由图4（b）累积距平曲线可知，2014 年是曲线发生显著变化的一年。因此，利用累计距平法也可将2014 年作为近13 a 东平湖蓄水量的突变点，结合M-K 突变检验法的判定结果，可进一步确定近13 a东平湖蓄水量发生突变的时间点为2014 年。将上述水位蓄水量突变点进行对比比较，得到了利用不同检测突变方法求得的水位、蓄水量基本一致的结论，并且水位与蓄水量突变的年份是相同的[14]。