电磁防护仿生中的神经动作电位发放特性

张明亮，张桂朋，王天怡，杨新梦，姚保成，闫杨阳

1.陆军工程大学石家庄校区电磁环境效应重点实验室，河北石家庄 050003；2.石家庄铁道大学机械工程学院，河北石家庄 050043；3.兰州交通大学光电技术与智能控制教育部重点实验室，甘肃兰州 730070

前言

随着电子设备中的导线、晶体管、电容、电感等电子元件越来越多，电路集成度越来越高，电子设备正常工作时向外辐射电磁场，使得设备所处的电磁环境变得越来越复杂［1］。为使电子设备在复杂的电磁环境中功能不被严重影响，需对其进行电磁防护。传统电磁防护方法，如接地、屏蔽、滤波等技术，尽管取得了较好的效果，但面对极其复杂的电磁环境时，仍不能满足防护的全部要求，在改善传统电磁防护方法的同时，探索基于全新的机理进行电磁防护具有十分重要的意义。

2002年，刘尚合等［2］以生物抗扰现象和行为为启发提出电磁防护仿生的构想，之后系统阐述电磁防护仿生的基本概念、技术基础、研究方法和研究目的以及可行性、必要性和重要性，明确提出电磁防护仿生的方向，为电磁防护提供一种全新的途径。由于电磁防护仿生的新颖性，尽管发展短短十余年，但已引起国内外众多学者的关注和支持，包括西北工业大学马远良院士、空军军医大学（第四军医大学）陈志南院士、西安电子科技大学段宝岩院士、北京航空航天大学苏东林院士等都给予了很高的评价。在电磁防护仿生研究中，神经系统的抗扰机制是其重要的理论基础，需要对其进行相关研究。

早在20 世纪50年代，Hodgkin 等［3-4］利用枪乌贼巨大神经突触做了大量的实验，提出神经元的数学模型，即Hodgkin-Huxley（HH）模型；此后，各种神经元模型被提出。神经元模型较多，但是由于HH 模型具有明确的生理含义和电路特征，易与电磁防护仿生研究相结合，故本研究重点利用HH 模型开展研究。

在神经元模型的基础上，易飞鸿等［5］运用数值模拟的方法研究了离子通道反转电动势参数变化对神经元发放动作电位的影响，结果表明疾病治疗可以在多离子通道的参数调解下进行。叶伟杰等［6］通过改进额叶视区网络模型（特定神经网络区域），研究多目标脑决策中的作用机制，并对多目标决策任务non-choice任务进行了仿真。徐桂芝等［7］运用经颅磁刺激技术进行一系列临床和生理研究，研究表明经颅磁刺激技术在治疗神经性疾病和脑科学研究中具有巨大潜力的应用价值。Zhang等［8］研究了神经元自治系统的稳定性，利用Lyapunov 稳定理论验证了神经元取生理学参数时HH 模型是渐近稳定的结论。尹晓楠等［9］对不同频率磁刺激对离体脑片神经元兴奋性及电压门控型钾通道影响进行了深入的研究，结果表明电压门控钾通道的动力学特征和神经元的兴奋性可能是磁刺激进行神经调控的潜在机制之一。乔帅等［10］对e-HR神经元模型的隐藏放电与分岔行为进行了研究，为HH 神经元模型的非线性动力学研究提供较好的研究思路。杜琳等［11］对于Izhikevich神经元模型的FPGA 硬件化进行了综述，为多种脉冲神经网络以及其他神经元模型硬件化实现提供了参考。赖策［12］提出基于漏积分点火模型、脉冲响应模型和概率脉冲响应模型，并对该模型进行了分析。谭红芳［13］对于HH 神经元在有无自调节突触作两种情况下对于外界刺激的相应进行了分析。

彭俊等［14］对于神经元膜电位信息编码进行了研究，该研究为神经活动信息量的定量计算提供了一种新的思路和方法。由于目前国内对于神经元的硬件化技术还不够成熟，所以很多实验需要参考生物实验上的结果。刘爱丽等［15］利用不同浓度下的氯化钾对于小鼠海马神经元膜电位变化进行了实验，实验结果表明，随着氯化钾浓度的增高，膜电位不断发生去极化，并且随着氯化钾浓度的升高，神经元兴奋性不断增强。伊国胜等［16］对于神经元中动作电位与信息编码之间的能量消耗进行研究，进一步解释了动作电位与信息传递的关系。韩姗姗等［17］利用HH模型解析了TMAS 下神经元的放电节律，结果表明：同一刺激电流密度下，随着电流的密度与频率比的增加，膜电势的幅值减小，并且随着电流的密度与频率比的增加，峰值差异越来越小。冀文超等［18］利用非线性理论对于神经元中混合簇的分岔机制进行了探讨，结果表明随着钙离子浓度的逐渐增加，全系统轨线在鞍结分岔曲线和同宿轨分岔曲线之间来回跃迁,是混合簇的产生分岔机制。刘畅等［19］对与神经元的放电行为和同步控制进行了研究，并设计了结果表明自适应同步控制器，结果表明当时滞和耦合强度取一定值时，给从系统施加非线性控制器,从系统在控制器作用下与主系统达到同步。吴静等［20］利用经典电路理论和介观电路的量子理论，推导了在外部冲击激励下神经元细胞膜电压响应的表达式，并将HH 模型中的一些参数代入其中，经过计算发现，介观电路模型更能反应神经元受到刺激后的生理特征。周秀颖［21］利用HH 模型，研究了在HH 神经元间用电突触耦合与化学突触耦合之间的相同点与不同点，为神经元形成神经元网络铺垫好了道路。

为更好地利用神经的抗扰机制进行电磁防护，本研究利用Simulink 搭建了HH 模型的求解程序，研究不同参数刺激下神经元的动作电位时域响应特性。通过改变外界刺激的参数研究神经元动作电位的发放模式规律及影响参数，探索神经元特有的行为和敏感参数，为基于神经元的仿生电路设计提供理论支持。

1 HH模型及搭建

1.1 HH模型

HH 模型是众多的神经元模型中具有代表性的模型之一，HH 模型是由4 个耦合作用的常微分方程组成的，数学表达式见式（1）：

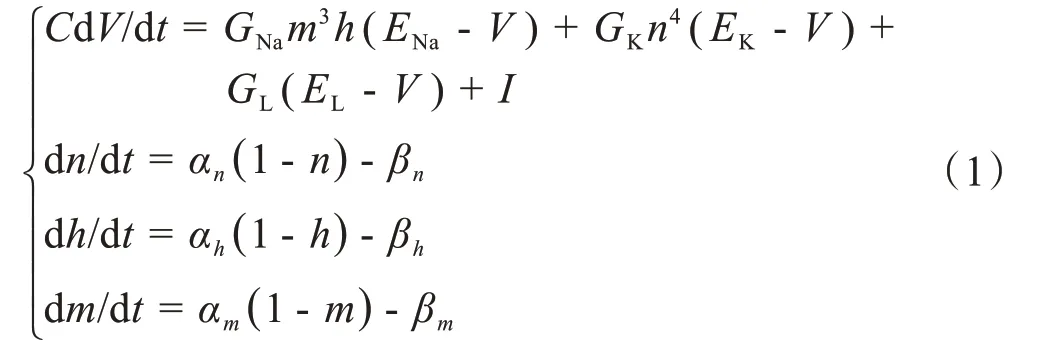
其中，C为神经元膜电容；V为神经细胞膜电位；t为时间；GNa为钠离子通道最大导电率；m为钠离子通道激活参数；h为钠离子通道不激活参数；ENa为钠离子通道反转电动势；GK为钾离子通道最大导电率；n为钾离子通道激活参数；EK为钾离子通道反转电动势；GL为漏电流电导；EL为漏电流反转电动势；I为外界刺激电流；α和β函数是与神经元膜电位有关的速率常数，α函数和β函数表达式见式（2）：

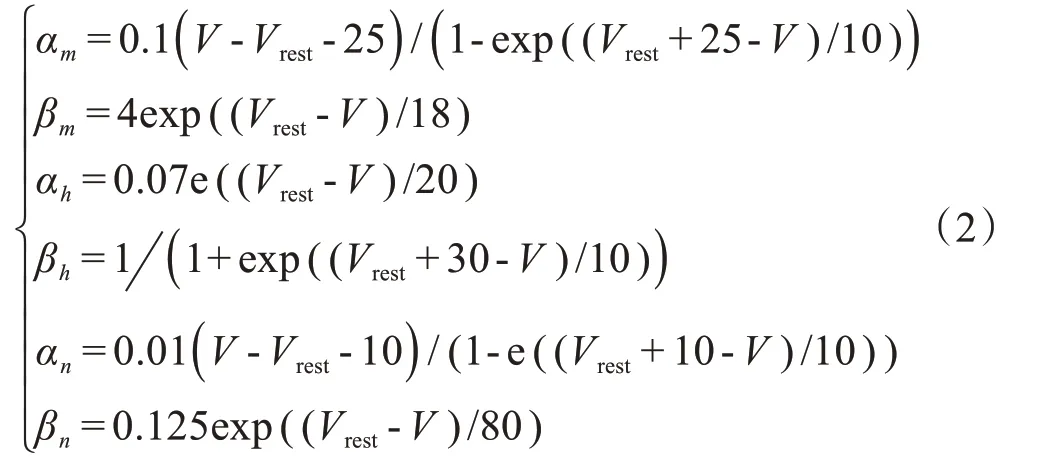
其中，Vrest为静息态动作电位。

根据生理学实验，本研究中HH 模型中各参数的取值见表1。

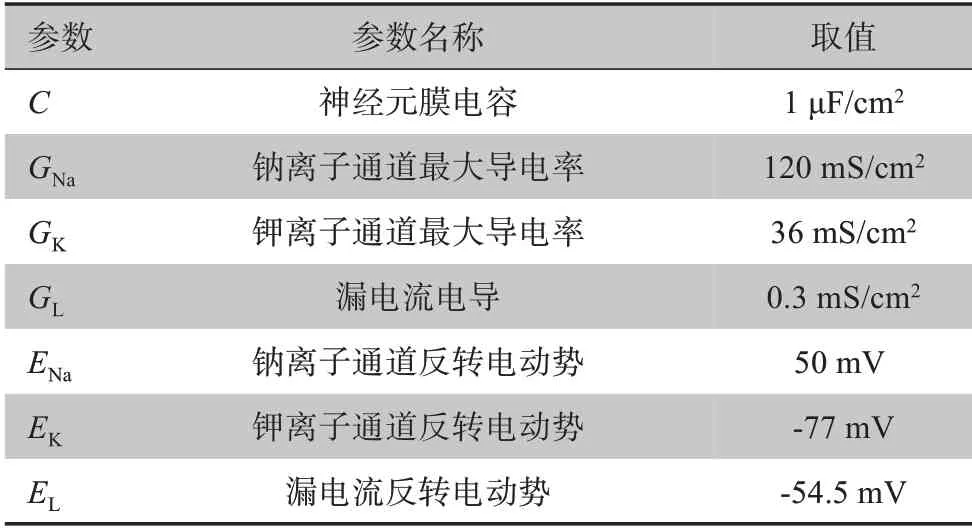
表1 HH模型中的各参数取值Table 1 Value of each parameter in Hodgkin-Huxley(HH)model

1.2 神经元模型建模

观察HH 模型的数学表达式，可知HH 模型方程具有强非线性和耦合性，对其解析求解十分困难。为探寻适合电磁防护仿生的规律，采用数值求解的方式对不同刺激信号下的神经元动作电位进行研究，以期达到寻找适合电磁防护仿生的特殊行为和敏感参数。本研究利用Simulink 搭建神经元仿真分析模型。HH 模型的动作电位受3 个激活系数m、h、n的影响，故仿真分析模型由3个模块组成。

图1为神经元仿真模型的总体框架，图2为模型图1中的3 个激活系数子模块。图2a 为钠离子通道活化参数，图2b为钠离子通道失活参数，图2c为钾离子通道活化参数。

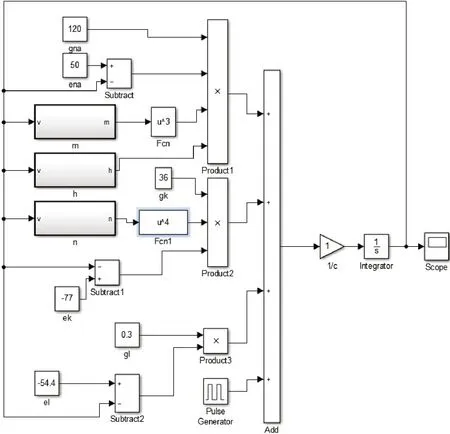
图1 HH模型整体程序图Figure 1 Overall programme flowchart of HH model

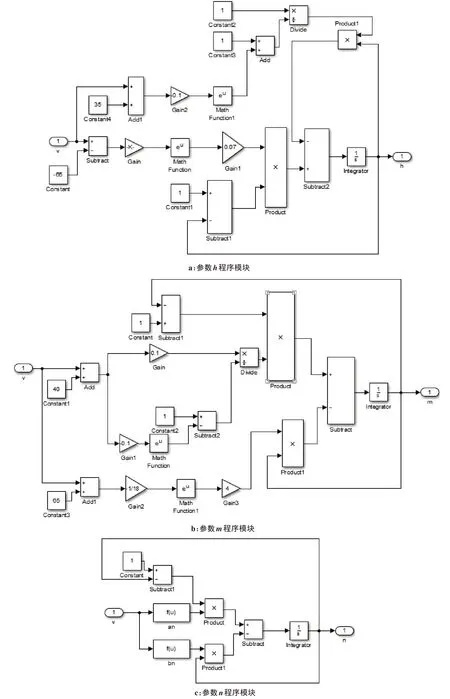
图2 模型中3个激活系数子模块Figure 2 Three activation coefficient submodules in the model

2 神经元动作电位发放特性仿真研究

在电生理实验中，方波刺激比较常见，实验结果具有一定的代表性，因此本研究以方波电流为外界刺激信号，重点研究方波的幅值、周期、占空比及刺激时长变化时，神经元的动作电位发放特性。

2.1 改变方波的幅值

方波参数中，方波的幅值是重要的参数，代表了刺激信号的强度。首先，研究幅值对神经元动作电位的影响。为具有较好的可比性，选定方波幅值为50 μA/cm2，刺激周期为10 ms，占空比为20%为标准信号，标准信号刺激下动作电位仿真计算结果如图3所示。

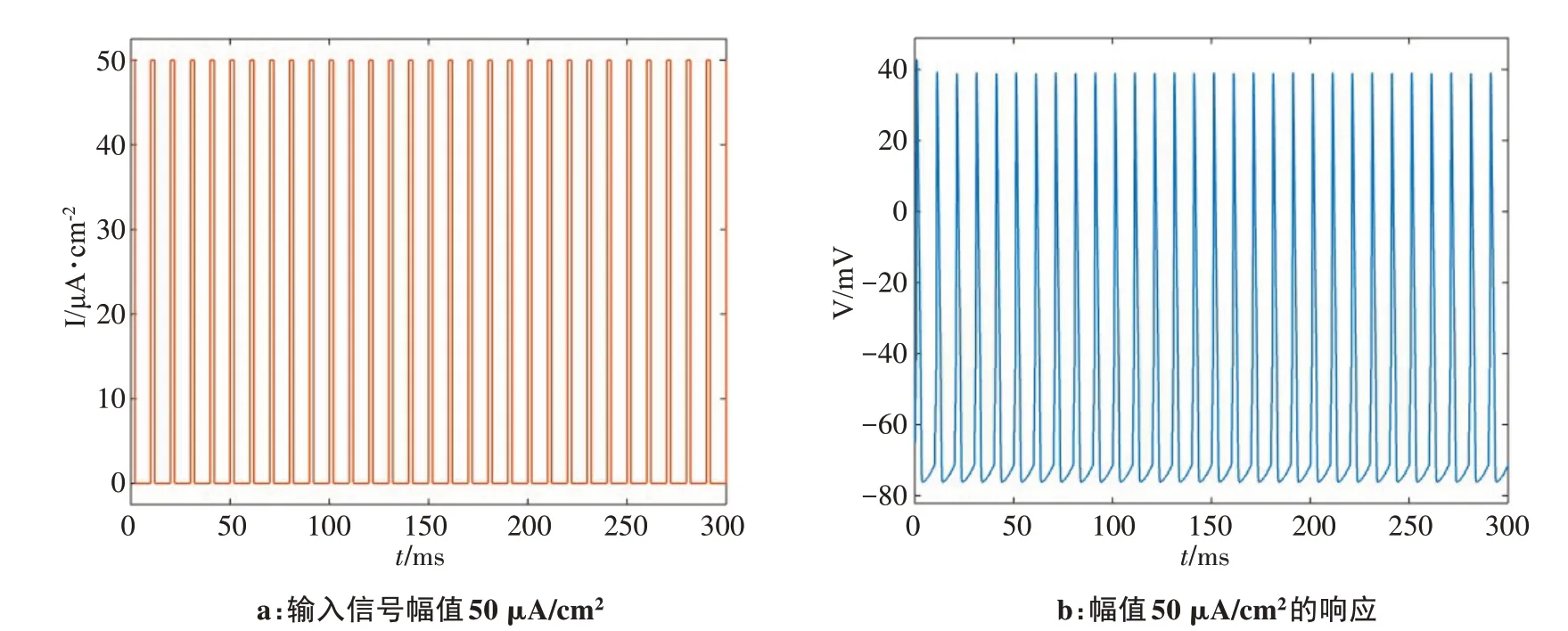
图3 标准信号刺激下动作电位响应Figure 3 Action potential response under standard signal stimulation

由图3可观察到神经元每受到幅值为50 μA/cm2，刺激周期为10 ms，占空比为20%的1次刺激时，神经元都会产生1次动作电位，神经元的动作电位从初始的幅值经历去极化达到正值，神经元此时进入绝对不应期，神经元此时再受到刺激，也不会产生动作电位；之后动作电位处于复极化，神经元经历复极化以后的电位相比静息电位还低；随后动作电位进入超极化［13］，神经元处于相对不应期，神经元在此期间只要受到足够强的刺激就会产生新的动作电位，随后复极化恢复静息态。神经元经历去极化、复极化、超极化和复极化4个过程完成1次动作电位的发放。

幅值从1 μA/cm2增长到3 μA/cm2，得到动作电位的响应特性，将其与标准信号刺激下的动作电位对比；再将幅值从4 μA/cm2增长到60 μA/cm2，同样与标准信号刺激下的动作电位对比，如图4所示。

通过多次仿真结果分析发现当外界方波幅值取14、20、21、40、60 μA/cm2时，HH神经元模型产生的动作电位会产生突变，即当方波幅值取4～13 μA/cm2、15～19 μA/cm2、21～39 μA/cm2、40～59 μA/cm2神 经 元产生的响应规律近似，便不再一一赘述。

当外界刺激幅值分别为1、2、3 μA/cm2时，HH 神经元只产生的局部电流，并未产生动作电位，如图4a～f，此时随着外界刺激幅值的增长，局部电流并未增长，验证了神经元响应的“无叠加”特性。

当刺激信号的幅值达到4 μA/cm2（图4h）时，神经元产生动作电位，但是此时神经元并不是每受到1 次刺激便产生1 次动作电位，而是在多次刺激下产生1次动作电位，故将这种能够产生动作电位但并非刺激周期与动作电位周期一一对应的参数定义为第一敏感参数。在前2 ms 的刺激下，神经元产生一个动作电位（尖峰），当动作电位达到峰值以后，由于神经元能量积攒不够，单个方波刺激不能产生动作电位，随着下一次刺激的到来（2 次刺激累积），神经元积攒了足够的能量，神经元动作电位才能激发。图4i、4j 分别为5、13 μA/cm2，发现随着刺激信号幅值的增大（幅值从4 μA/cm2到13 μA/cm2），可在中间时刻（10～20 ms 时）产生小的凸起，且凸起程度越来越大，由此可以得知神经元在外界刺激信号下积累的能量越来越多。继续增大刺激信号幅值，当其达到14 μA/cm2时，图5k），其中某个凸起变为动作电位，此时可将3次刺激（20～50 ms和50～80 ms）看为一个周期，前2次刺激都产生了动作电位尖峰，后1次刺激未能产生动作电位尖峰，这时神经元同样进入能量积攒期。同样的现象也出现在幅值18 μA/cm2和19 μA/cm2。当幅值增长到18 μA/cm2时，如图4l），此时将4 次外界刺激当作1个周期，前3次产生动作电位，这3次动作电位的峰值依次减小，第4 次产生局部电位，随后神经元进入能量积攒期。当刺激信号幅值为19 μA/cm2时，神经元在受到10 次刺激时，会产生8 次响应，此时将5次刺激看作1个周期，其变化规律和18 μA/cm2、14 μA/cm2相似。当刺激信号的幅值为20 μA/cm2时，神经元产生的动作电位可以将11 个信号值看作1 个大周期，前10个都会产生动作电位，而第11个产生局部电位。当刺激信号幅值达到21、40、60 μA/cm2时，此时神经元每受到1 次刺激就会产生1 次响应，此时将这种能产生尖峰并且刺激周期与动作电位周期一一对应的参数定义为第二敏感参数。

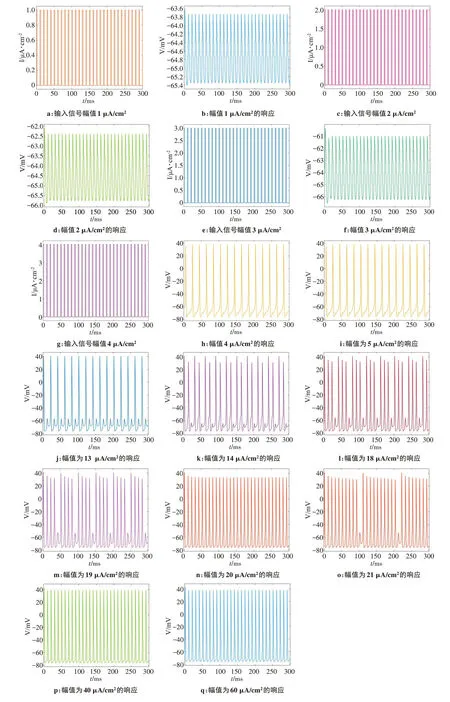
图4 不同幅值下动作电位响应Figure 4 Action potential response at different amplitudes

由以上现象可以得出神经元的动作电位发放特性和外界刺激信号的强度有关，当强度越大，相对不应期将会越短。当刺激信号幅值大于第一敏感参数时，神经元受到的刺激信号周期和产生的动作电位信号周期之比不是1：1 而是处于N：1（N＞1）；当刺激信号强度大于第二敏感参数时，神经元受到的刺激信号周期和产生的动作电位信号周期之比是1：1。根据第一敏感参数和第二敏感参数的定义，本研究得到幅值的第一敏感参数为4 μA/cm2和第二敏感参数为21 μA/cm2。需要说明的是这两个值发生的条件是：神经元取生理参数（导电、电容、反电动势等）、周期为10 ms、占空比为20%。当神经元模型参数和刺激周期与占空比发生变化时，其幅值的第一敏感参数和第二敏感参数会发生变化，需进一步研究。

2.2 改变周期

在研究幅值对动作电位影响的基础上，研究周期对动作电位的影响。幅值固定为50 μA/cm2，占空比固定为20%，将外界刺激信号的周期从1 ms 每次增加1 ms增长到10 ms，随后从10 ms每次增长10 ms增长到200 ms，仿真结果如图5～7所示。

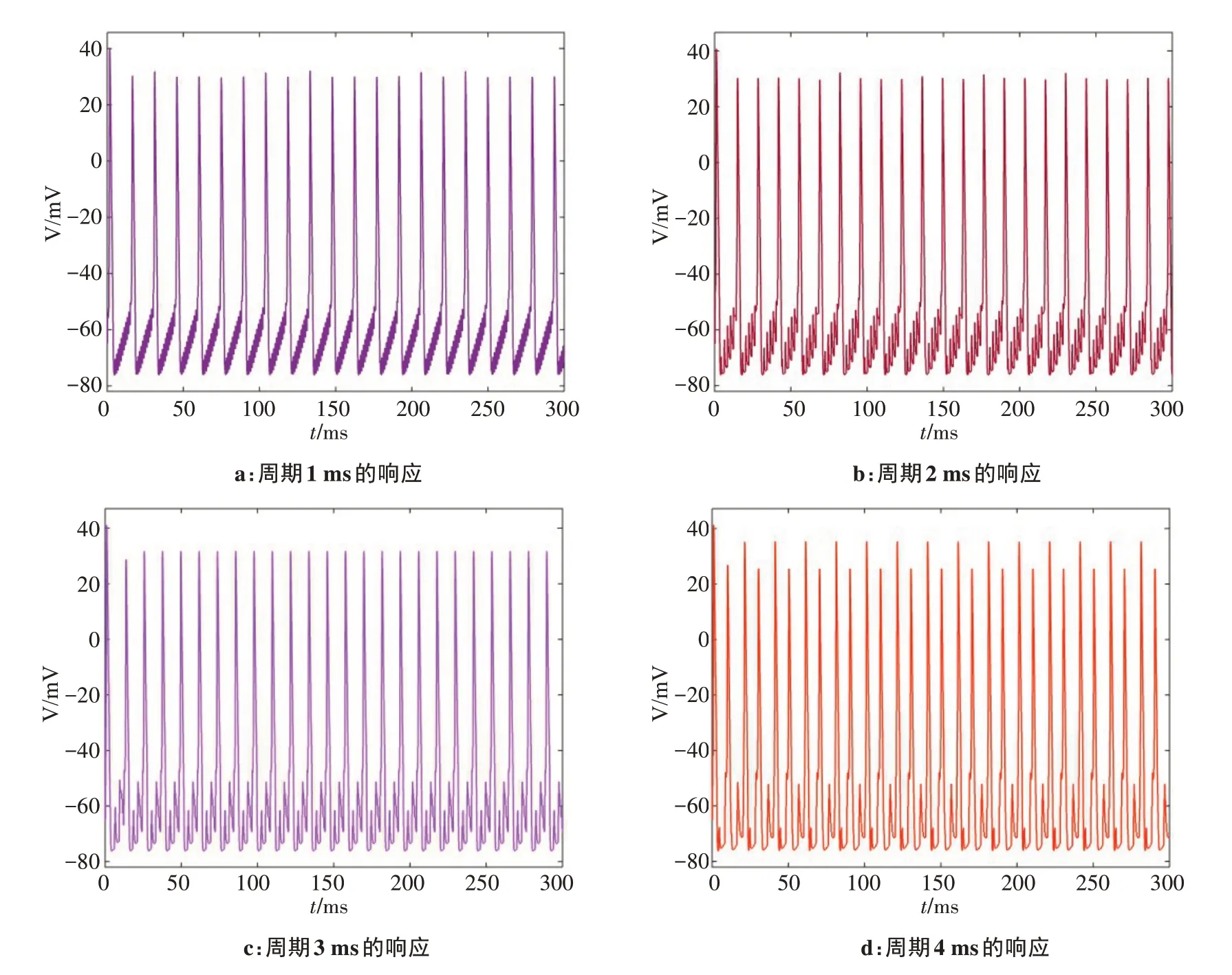
图5 周期为1～4 ms时动作电位响应Figure 5 Action potential response in periods ranging from 1 ms to 4 ms

随着刺激信号周期的增加，神经元的相对不应期变短，神经元在受到周期为1 ms 的信号刺激后，立刻产生了第一个动作电位，第二个动作电位在15.4 ms 时产生，第三个动作电位在30.2 ms 时产生。由图5b 可以观察到当神经元受到刺激信号周期为2 ms 的信号刺激时，立刻产生了第一个动作电位，第二个动作电位在14.2 ms产生，第三个动作电位在26.4 ms 产生。相比之下，周期为2 ms 的刺激响应比周期为1 ms 的刺激响应第二个动作电位提前了1.2 ms，第三个动作电位提前了3.8 ms。图5c 为周期为3 ms 的响应特性，第二个动作电位在13.7 ms 时发生，第三个动作电位在25.6 ms 时发生。图5d 为周期为4 ms 的响应特性，第二个动作电位在10.1 ms 时发生，第三个动作电位在21.3 ms 时发生。周期为4 ms的刺激响应相比周期为3 ms 的刺激响应，第二个动作电位提前了3.6 ms，第三个动作电位提前了4.3 ms。由此可知相对不应期的时间和刺激信号的周期成反比。

由图6a 可以观察到当刺激信号达到5 ms 时，神经元在相对不应期的叠加性消失，但是这时相对不应期产生一次局部电位的变化；当刺激信号的周期变为6 ms时（图6b），神经元响应出现特殊情况，神经元的局部相对不应期时间变长；当刺激信号的周期变为7 ms时，神经元响应类似于图4m，此时将4次外界刺激当作1个周期，前3次产生动作电位，这3次动作电位的峰值依次减小，随后进入不应期；当刺激信号的周期变为8 ms时，神经元在每受到1次刺激神经元就会产生1次动作电位。按照敏感参数的定义，可得8 ms为周期的第二敏感参数。

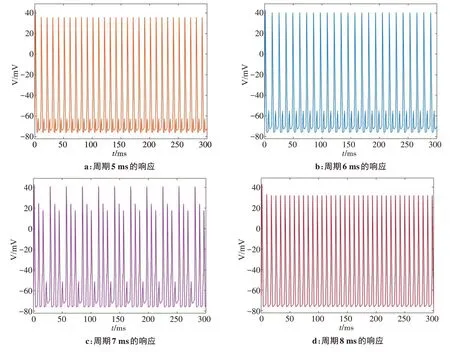
图6 周期为5～8 ms时动作电位响应Figure 6 Action potential response in periods ranging from 5 ms to 8 ms

由图7a、b可以观察到当刺激信号周期为20 ms时，神经元在每次受到刺激时都会产生1 次动作电位。但是随着刺激信号的周期增大到50 ms时，如图7c、d，神经元受到1 次刺激产生了2 次尖峰；当周期变为100 ms时，如图7e、f，神经元受到1次刺激产生了3次尖峰；当周期为200 ms，如图7g、h，神经元受到1次刺激时产生了5 次尖峰，并且产生的动作电位的第1 个峰值远大于其余峰值，表明神经元在受到刺激的时候，并不会一直处于响应，而是会进入不应期，并且在一段持续刺激下，神经元第2次动作电位的强度远小于第1 次。周期大于等于50 ms 时，动作电位的发放模式由单个尖峰脉冲周期发放模式变成了几个尖峰集中脉冲隔一定周期重复发放模式，即簇发放模式。其产生簇发放的原因在于占空比固定的情况下，周期越大，刺激时长越长。如周期为200 ms，占空比为20%时，刺激时长达40 ms；而周期为50 ms，则刺激时长只有10 ms。长时间的刺激使得神经元产生了多个尖峰连续出现，但由于神经元具有恢复静息态趋势，第二尖峰表现为与第一个尖峰不一样的行为。由图4、图7d、f、h 观察到当刺激信号幅值达到第二敏感参数以上时，神经元产生的动作电位的第1 个峰值稍大于第2 个及以后的峰值，其原因在于当神经元受到外界刺激时，钠离子内流，产生动作电位，当钠离子通道关闭以后，细胞外的钠离子开始恢复原始浓度，由于恢复时间较短，钠离子浓度低于初始值，所以产生的动作电位第2个峰值小于第1个。当刺激周期足够大，相邻的两次刺激时间间隔足够长，如图7a，神经元有了足够的恢复时间，神经元外的钠离子浓度可以恢复到没有受到刺激时的浓度，当神经元再受到刺激时，其动作电位发放呈现周期性。

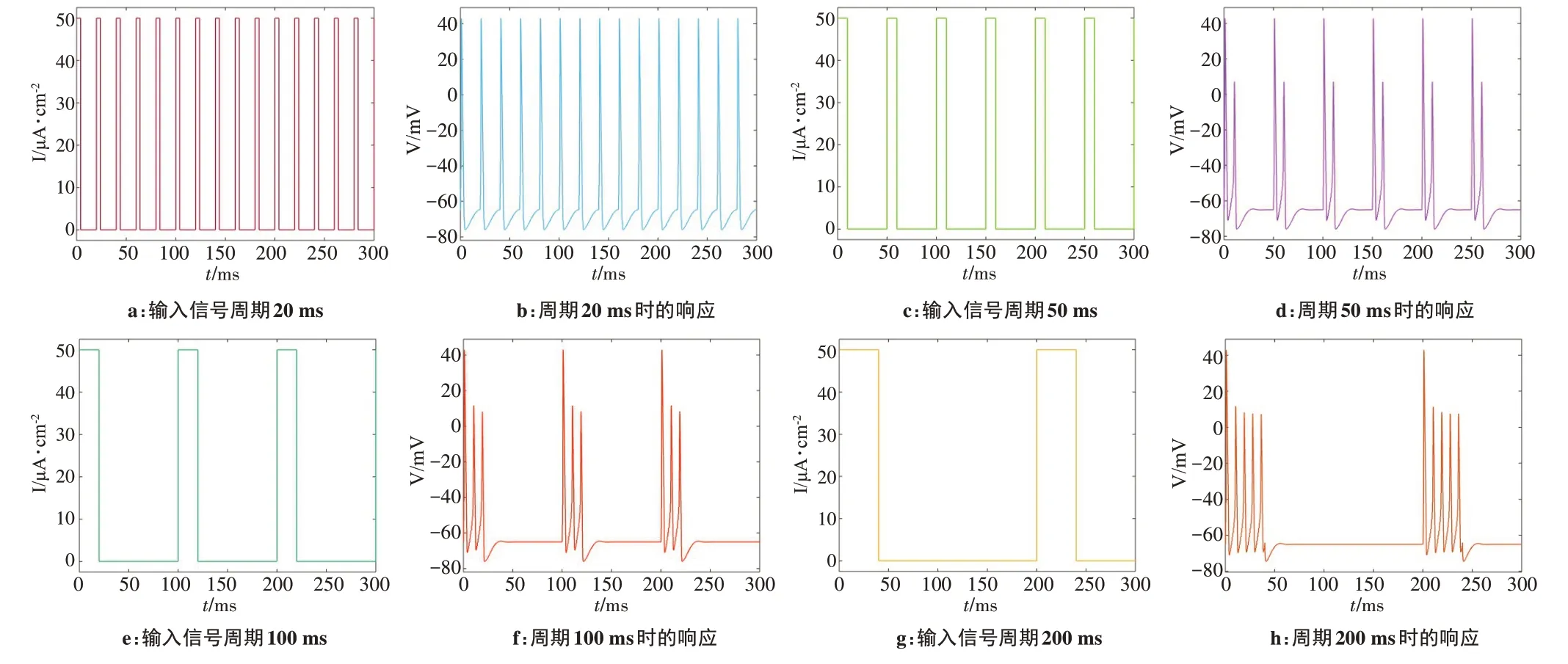
图7 周期为20～200 ms时动作电位响应Figure 7 Action potential response in periods ranging from 20 ms to 200 ms

2.3 改变占空比

占空比是方波信号重要参数，本节研究占空比对动作电位的影响。幅值固定为50 μA/cm2，周期固定为10 ms，改变占空比从1%增加到30%，仿真计算结果如图8所示。

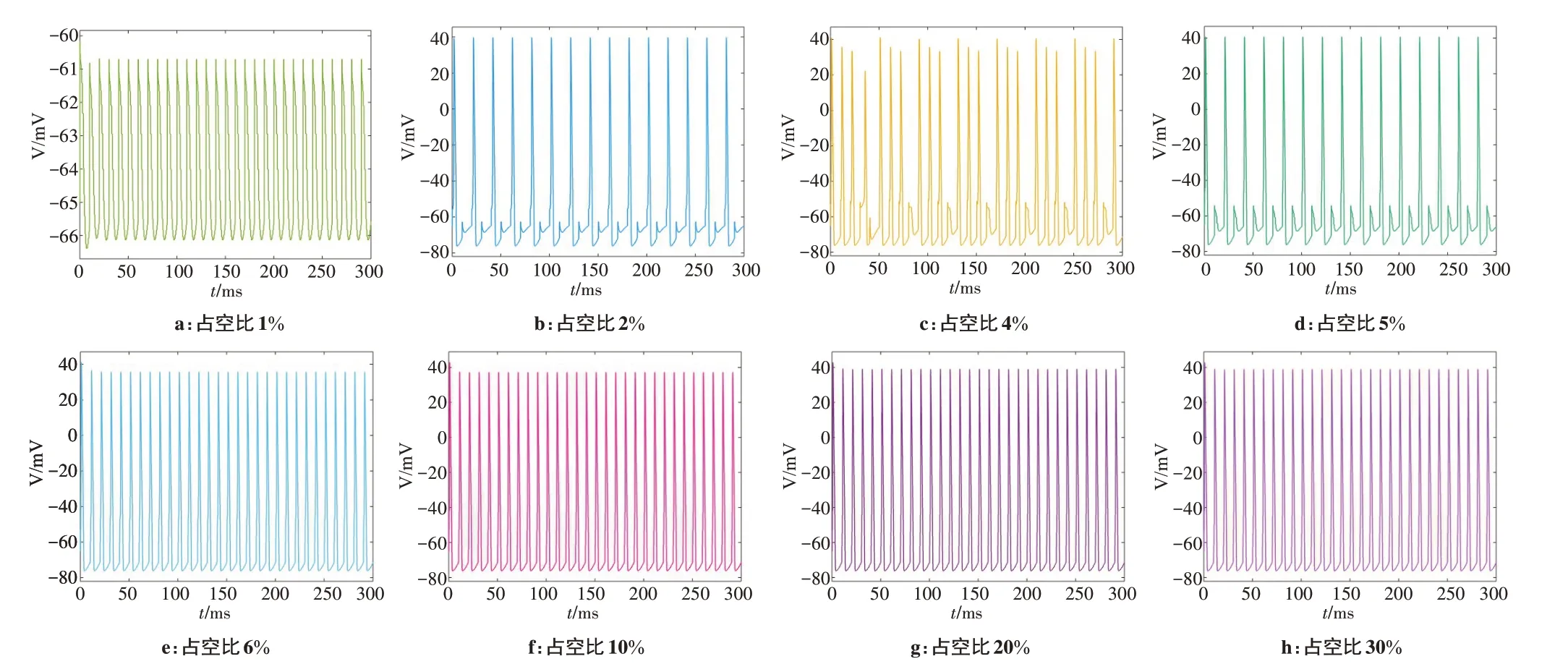
图8 占空比对动作电位的影响Figure 8 Effects of duty cycle on action potential

由图8a 可以观察到当外界刺激信号的周期为10 ms，占空比为1%时，此时虽然刺激信号的幅值大于幅值的第二敏感参数，但是每个周期的刺激信号中有效时间太短，积累的能量较少，所以神经元刺激后的变化电位为局部电位，没能激发出动作电位。当占空比达到2%时（图8b），刺激信号大于幅值的第二敏感参数，神经元能够产生动作电位，并且在产生一次动作电位以后随即进入不应期，产生局部电位，此时再受到刺激时，神经元又会产生新的动作电位。占空比增长到4%时（图8c），两个尖峰之间的凸起程度越来越大。当刺激信号的占空比增长到5%时（图8d），可将5 次外界信号刺激看作1 个周期，前4 次产生逐渐减小的动作电位，第5次产生局部电位。随着占空比的增加，外界信号的刺激时长增大，神经元的动作电位响应也逐渐增强。当刺激信号的占空比达到6%、10%、20%、30%时（图8e～h)，神经元每受到1次刺激就会产生1 次动作电位，由此可得6%为占空比的第二敏感参数。

2.4 相同刺激时长

方波刺激时，主要的参数分别为幅值、周期以及占空比。当周期和占空比都不同时，但是两者的乘积可能相同，即二者所得到的有电流持续时间（刺激时长）可能相同，因此本节研究相同刺激时长对神经元的动作电位的影响。刺激时长为5、6、8、10 ms 时的仿真结果如图9所示。

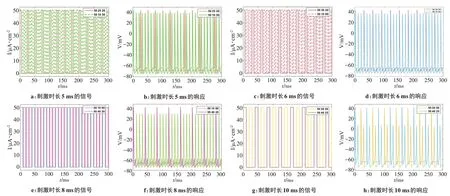
图9 同时长刺激下产生的动作电位Figure 9 Action potential generated by the same duration of stimulation

图9a、b表示的是幅值为50 μA/cm2、周期为25 ms、占空比为20%的外界刺激信号和幅值为50 μA/cm2、周期为10 ms、占空比为50%的外界刺激信号，两者的刺激时长都为5 ms。图9c、d 表示的是幅值为50 μA/cm2、周期为30 ms、占空比为20%的外界刺激信号和幅值为50 μA/cm2、刺激周期为10 ms、占空比为60%的外界刺激信号，两者的刺激时长都为6 ms。图9e、f 表示的是幅值为50 μA/cm2、周期为10 ms、占空比为80%的外界刺激信号和幅值为50 μA/cm2、周期为40 ms、占空比为20%的外界刺激信号，两者的刺激时长都为8 ms。图9g、h 表示的是幅值为50 μA/cm2、周期为20 ms、占空比时间为50%的外界刺激信号和幅值为50 μA/cm2、周期为40 ms、占空比时间为25%的外界刺激信号，两者的刺激时长都为10 ms。不管外界刺激信号的周期多大，只要在一个周期中对于处于有电流（I＞0 时）的两个外界刺激信号时间段内，神经元系统产生的动作电位是完全相同的。但是因周期不同，在小周期信号出现有电流时，大周期信号出现无电流时，这时只有小周期刺激信号产生动作电位和局部电位。从这个现象可以得到刺激时长同样是决定动作电位和局部电位产生的重要因素，这些规律和现象为基于电磁防护仿生的仿生原型电路提供理论支撑。

3 结论

本研究对面向电磁防护仿生的神经元动作电位发放特性进行研究，利用Simulink工具箱搭建神经元的HH 模型，研究方波信号的幅值、周期、占空比及刺激时长对神经元动作电位的影响。通过研究得到一些结论：（1）发现了第一敏感参数和第二敏感参数现象，幅值的第一敏感参数为4 μA/cm2，第二敏感参数为20 μA/cm2；（2）验证了神经元具有“全和无”、“无叠加性”、“不衰减传导性”的机制；（3）发现了周期的第二敏感参数为8 ms 和占空比的第二敏感参数为6%，且第一敏感参数和第二敏感参数受到幅值、周期和占空比综合影响；（4）发现了刺激信号周期与动作电位发放周期之比不为1 和动作电位的簇发放模式的现象；（5）得到了信号刺激时长同样是决定动作电位发放的重要因素。这些研究结果为电磁防护仿生提供了理论基础，为基于神经元的仿生原型电路设计提供依据。