基于动态SSI模型和ADT相结合的可靠性预测方法研究∗

张国龙 吕 鑫 方 远 石景岚 朱 峰

（电子信息系统复杂电磁环境效应国家重点实验室 洛阳 471003）

1 引言

产品的性能和可靠性主要受实际工作环境应力的影响，如何建立更加贴近产品实际工作环境的可靠性预测模型是当前研究的重点。现有文献关于可靠性分析预测的模型大多数局限于产品工作环境应力是确定性和静态应力水平的假设条件下［1～4］，模型对于在实验室进行的环境可控的加速试验适用性强，但不适用于分析产品在时变环境下的可靠性，在工程实际中，产品的工作环境应力具有时变性。应力-强度干涉模型起源于机械可靠度领域，利用应力与强度之间的关系定量评估产品可靠性，多应用于可靠性强化试验，传统的应力强度模型只能大概描述产品可靠度曲线，主要应用于机械类产品的磨损可靠性预测［5～8］，很少应用到电子产品的可靠性预测中，一方面缺乏试验数据的支持，另一方面，大部分研究中的应力和强度都是广义上的，即应力是指所有导致产品失效因素的综合，而强度则是抵抗这种失效的能力。一般通过加速退化试验可获得恒定应力下受试产品的可靠性变化曲线，本文结合恒定应力加速退化试验和动态应力强度模型理论，外推得到产品工作环境服从正态分布时的可靠度随时间的变化趋势。

2 应力-强度干涉模型

定义［9～10］：产品的失效取决于使用应力和强度之间的关系，当产品强度大于环境应力时，能够正常工作，反之则不能正常工作，假设产品的强度为Y，使用应力为X，则产品的可靠度可表示为

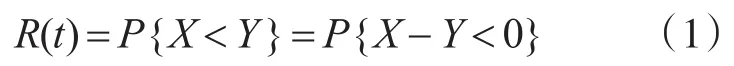
假设Y和X都符合正态分布，令Z=Y-X，则根据正态分布的和（差）仍为正态分布的性质，可知Z也符合正态分布，其Z的密度函数为

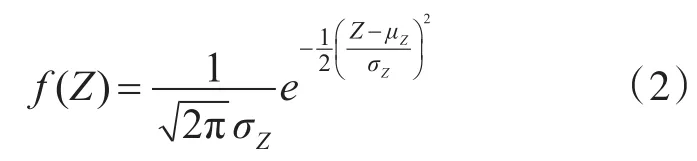
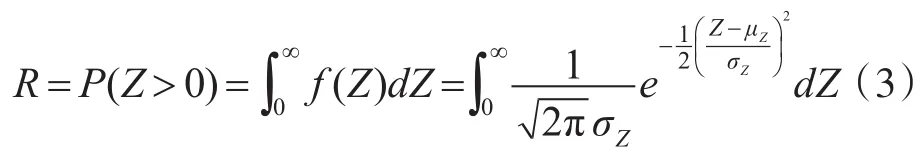
将式（3）转换为标准正态分布形式：

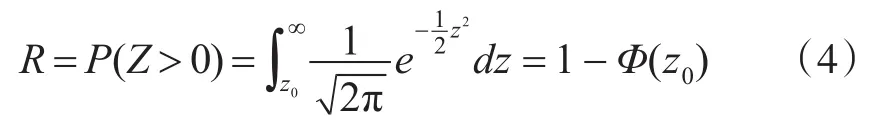
从式（4）可以看出，静态SSI模型与时间变量无关，而通常所讲的可靠性是一个与时间变量相关的概念，因此这种模型只能定量评估产品的性能可靠性。然而很多产品在实际使用时会受疲劳、劣化、侵蚀等方面因素的影响，强度会随着使用时间在应力作用下逐渐发生退化，此时静态SSI模型已不能适用于评估产品使用可靠性，因此，考虑应力作用下强度随时间退化的动态SSI模型更加符合工程实际，此时引入应力和强度随时间变化的动态应力-强度干涉模型，如图1所示，动态SSI模型的示意图，由式（1）变为随时间变化的可靠度：

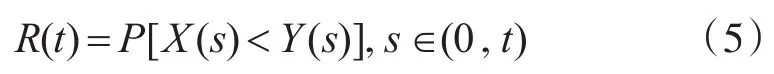
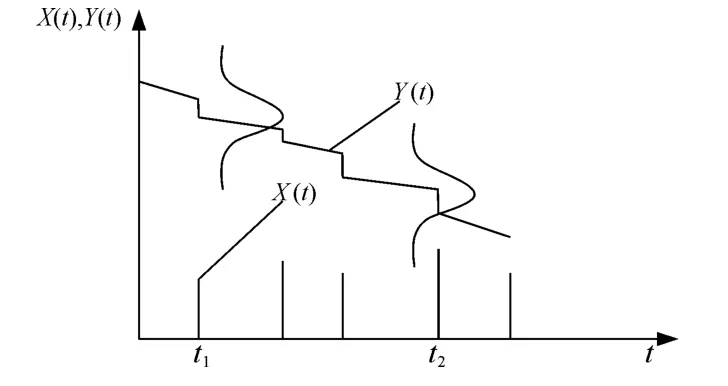
图1 动态应力-强度模型示意图

文献［9］将产品的强度和应力分别用两个随机过程来描述，如式（6）所示。

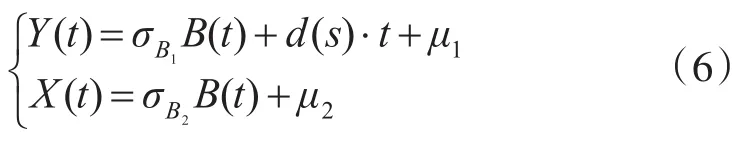
其中，B（t）是均值为0，方差为时间t的标准布朗运动；σB为扩散系数，σB1表征产品的强度随时间退化的随机性，σB2表征应力随时间变化的随机性；d（s）为漂移系数，是一个与应力相关的确定性函数，μ1为产品强度的初始值，μ2代表应力的初始值。

根据式（4），结合布朗运动首次达到阈值时间的分布，可推导得到产品在时间区间（0，t0）内工作的可靠度模型：

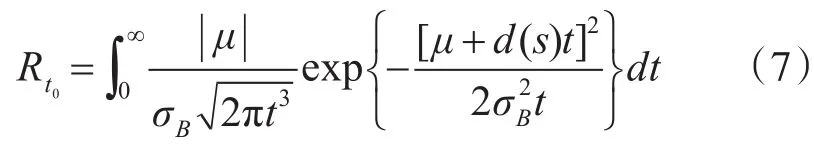
从式（7）模型中可以看出，虽然考虑了应力和强度随时间变化的情况，但是由于假设应力和强度均为随机过程，因此需要通过数值积分的方法来求解可靠度值，而且求解过程非常复杂，且随机过程的参数估计误差偏大，虽然具有一定的通用性，但是与工程实际很难有效地结合到一起，因此，本文结合动态SSI模型和加速退化试验理论，在产品环境应力服从正态分布的假设下，提出一种定量预测产品可靠性的方法。

3 基于动态SSI模型的加速退化试验可靠性定量预测

通常利用加速应力试验最终只能给出产品在恒定应力水平下的可靠度变化曲线，而动态应力强度模型相对于传统应力强度模型可以分析应力随时间变化条件下的可靠性问题。因此将应力强度模型应用到加速性能退化试验可靠性分析中，利用恒定应力加速退化试验数据得到产品可靠度的前提下，通过SSI模型外推得到产品在各应力水平下强度随时间退化的数据，此时强度是指产品在应力极限值，也是耐受强度，推导产品在动态环境作用下的可靠性。

首先作如下假设：

1）产品实际工作环境的应力服从正态分布N(uE,δE)；

2）产品的失效主要来源于环境应力，不考虑其他方面因素的影响；

3）与环境应力所对应的强度即产品的环境应力耐受强度，如只考虑温度环境应力因素的影响，则此处强度即为温度应力极限值。

4）在k个应力水平下进行加速退化试验，每组应力水平有n个试验样本，假定在给定时刻性能退化量的标准方差和强度的标准方差一致。产品的强度退化量与应力大小的关系一般服从加速模型［11］，且产品性能特征量和应力强度都能够反映产品的性能退化好坏，因此，两个物理量量纲不同，反映的物理意义相同，因此，对性能退化量进行无量纲化处理后，假定标准方差一致是合理的［12］。

基于上述假设，动态环境下的可靠性预测步骤如下：

第1步：根据加速退化试验的数据，获得给定时刻下各样本的性能退化量的均值和方差；

第2步：根据性能退化分析技术，获得每组恒定应力水平S1,S2,...,Sk下的可靠度函数值R1(t),R2(t),...,Rk(t)，在已知的测试时刻t1,t2,...,tm，抽取各应力下的可靠度函数值，如图2所示，组成如下数据序列：

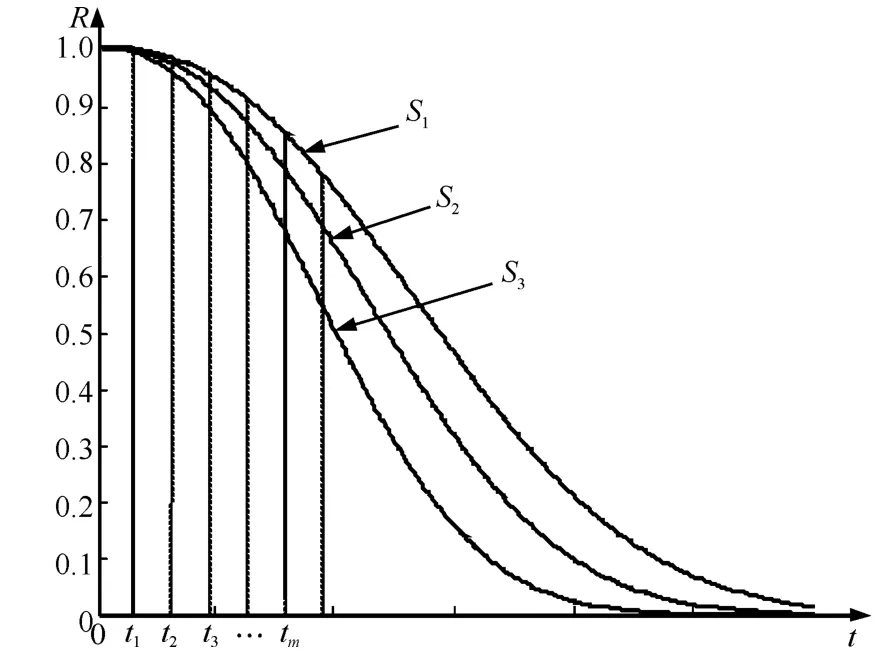
图2 通过恒定应力加速退化试验得到可靠度曲线

第3步：根据SSI模型外推产品在各应力水平S1,S2,...,Sk下，在给定时刻t1,t2,...,tm的强度值。

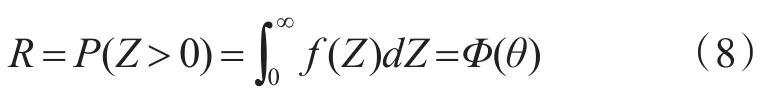
因为产品是进行恒定应力加速退化试验，因此环境应力是恒定不变的，则在应力水平S0下在给定时刻tj时刻，应力水平的均值μX(tj)=S0，σX(tj)=0。

令R(tj)=Φ(θ)，即可反推得到θ的值，由θ的定义式可推导得出：

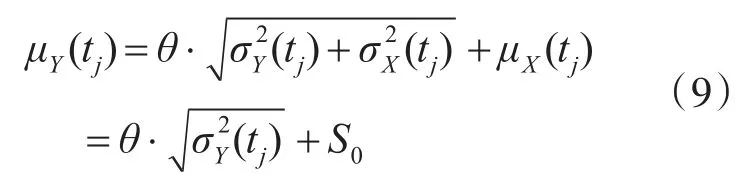
这样就获得产品在强度均值数据和方差数据：μY(tj)，j=1，2，…m。

由上述过程就可外推得到产品在各应力水平下，在各时刻强度的均值数据。利用这些均值数据，就可以得到强度随时间变化的曲线，选择指数模型y=a∙xb+c回归拟合强度退化曲线。

第4步：外推正态分布环境应力水平下的可靠度曲线，通过蒙特卡洛仿真的方法进行可靠性预测，方法步骤如下：

子步骤1根据产品强度退化曲线的回归参数a，b，c的估计值，利用蒙特卡洛仿真的方法生成N个强度数据，假定产品工作的正常应力服从正态分布S0～N(μE,σE)，同时利用蒙特卡洛仿真方法产生N个应力数据；

子步骤2 令y=S0，即：对两边取对数，简化可得到失效时间数据：

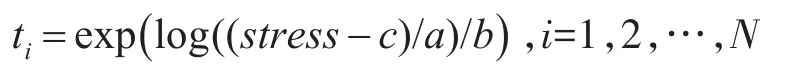
子步骤3则在给定任意时刻top，定义τi如下：

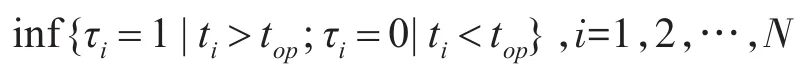
则根据产品可靠度的定义，得到可靠度值为

4 实例分析

某电子产品经过分析确定其失效主要是由于温度环境应力引起，其工作时的温度环境应力大致服从N（20，1.22）的正态分布，所以选择温度应力作为加速应力水平进行加速退化试验，选取10个样本，在5组应力水平下进行加速退化试验，根据上述方法预测产品的使用寿命。

通过加速退化试验获得产品在正常应力水平下的可靠度函数为

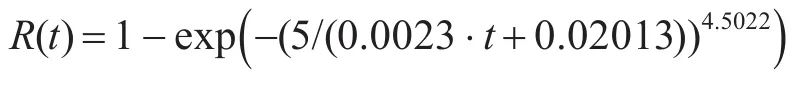
按照上述方法，外推产品的强度数据，利用指数回归拟合方法得到强度退化曲线如图3所示，参数估计值如表1所示。

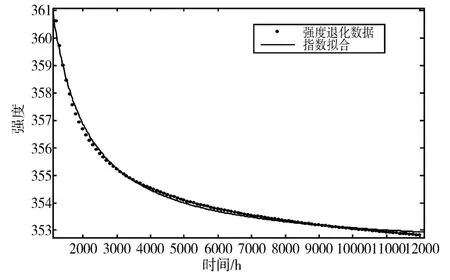
图3 强度退化曲线

表1 参数估计值

根据步骤4中基于MC仿真的方法，得到产品在温度应力服从正态分布N（20，1.22）时的可靠度曲线如图4所示。

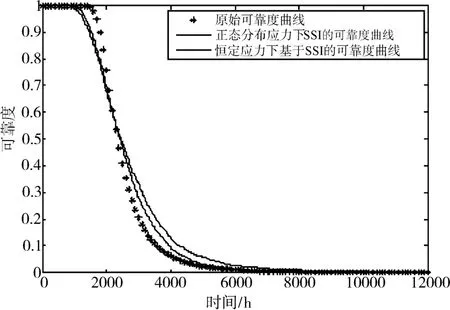
图4 环境应力正态分布假设下的可靠度预测曲线

根据均值和方差及SSI模型的定义得到各应力水平下的可靠度函数，和通过加速退化试验获得的可靠性曲线对比分析，证明了上述外推强度退化数据方法有效性。同时根据SSI模型的定义外推环境应力服从正态分布情况下的可靠度曲线，表明产品在动态环境下的可靠度与恒定应力水平下的可靠度存在较大差异。

5 结语

利用加速退化试验通常只能给出产品在恒定应力水平下的可靠度变化曲线，而动态应力强度模型相对于传统应力强度模型可以分析应力随时间变化条件下的可靠性问题。本文将应力强度模型应用到加速性能退化试验可靠性分析中，利用恒定应力加速退化试验数据得到产品可靠度的前提下，通过SSI模型外推得到产品在各应力水平下强度随时间退化的数据，推导出产品在动态环境作用下的可靠性。相关理论方法应用到工程实际可有效提高产品使用寿命预测的有效性和准确性。