基于综合评价法的两栖作战直升机着陆区选择决策模型∗

刘贵兵 田千华

（1.海军指挥学院 南京 210016）（2.92941部队 葫芦岛 125001）

1 引言

两栖作战中运用直升机超越上陆，可充分发挥直升机机动性、高速性，达成超越敌海岸线直达浅近纵深地域的目的，是现代两栖作战中重要的上陆方式［1］。在作战筹划中，合理选择两栖作战直升机着陆区，是达成两栖作战企图的关键步骤，也是夺取战场主动权要重环节。运用科学的分析评价方法，有利于在作战决策中提供可靠参考，为指挥员提供选择决策依据。

2 直升机着陆区选择决策方法分析

两栖作战中直升机着陆区选择与登陆区域选择有相似的模糊决策特性，该类问题的决策算法较为丰富［2］，以往学者在研究中给出较多解决该类问题的决策方法。徐泽水、尹钢等［3～4］采用三角模糊数型多属性决策方法，在基本因素权重不确知情况下，以三角模糊数代表主观偏好值和属性值，基于相似度方法构建线性规划模型，最终得到决策方案优劣排序。方绍琨、宋剑等［5～6］运用多目标决策模型和非线性规划优化理论，融合主观评价与客观条件，建立不完全信息的各登陆点多目标决策的非线性规划模型，得到决策方案的优化排序。倪艳等［7］采用灰色局势决策方法，通过主观偏好值加权效果测度矩阵，投影至理想值获取决策方案的优劣排序。本文旨在提出提出将D-S证据理论与AHP法相结合，探寻一种有效消除冲突证据偏差，减弱模糊决策问题主观性影响的方法。

3 直升机着陆区选择决策指标分析

直升机着陆区域选择决策属于典型的模糊判断问题，影响决策的因素较为多元，综合分析相关研究内容［8～9］，选择决策指标构成可基本概括为战术突然性、敌对空防御火力部署、着陆区条件和指挥协同难度。在具体决策评价中，需选取若干从业专家或经验丰富的指挥员，立足两栖作战全局，分别评价各方案的指标。

3.1 战术突然性

达成战术突然性是实现两栖作战企图的重要举措，是夺占两栖战场优势的重要途径。达成战术突然性主要是通过合理规划直升机航线，尽可能避敌有效侦查范围，在敌意想不到的方向上陆，以极大减小行动的暴露程度，同时要尽可能保证对敌要害部位的有效威胁。

3.2 敌对空防御火力部署

直升机着陆区的选择应充分考虑敌方对空防御火力的部署，航路规划时应尽可能避开敌对空火力打击范围，以最大程度保证登陆兵上陆行动的安全。两栖作战中，敌主要以飞机和防空导弹作为中远程防御手段，以近程导弹、高炮或直瞄武器作为近程防御手段。在直升机编队实施超越登陆时，若航路上敌对空火力密集，必然会造成垂直登陆兵力的一定程度损失。因此，筹划直升机着陆区选择时，应尽可能选择敌对空防御较为薄弱的区域。

3.3 着陆区条件

直升机着陆区是直升机编队或波次着陆、展开，发展后续进攻的区域，两栖作战中直升机着陆区应具备一定的条件。一是着陆区应具备场地条件，场地应具有足够的开阔性和平坦性，以满足直升机着陆需要；二是着陆区应具备一定的遮蔽条件，使敌难以及时察觉，保证着陆行动的顺利实施；三是着陆区应具有一定的净空条件，保证直升机着陆过程的安全。

3.4 指挥协同难度

两栖作战中，参与兵力多元，作战环节复杂，对指挥精度和协同程度要求较高。选择直升机着陆区应当充分考虑垂直登陆兵力和平面登陆兵力的协同问题，以及登陆兵与海空火力支援、综合保障等兵力的协调性，以及首波上陆兵力与后续上陆兵力的衔接关系等。此外，还应考虑指挥能力、通信水平以及各级指挥员能力，保证两栖作战各环节的耦合性和过程的连续性。

4 最优着陆区选择决策模型

直升机着陆区选择属于多属性约束条件下的模糊决策问题，可运用D-S证据理论将决策模型中多个相关联的指标进行融合［10］，通过算法消除证据冲突，为有效选择决策两栖作战中直升机着陆区提供依据，此方法适用于解决此类最优决策选择问题。

4.1 改进D-S证据决策模型

设辨识框架 Θ={θ1,θ2,∙∙∙,θn}，是由n个完备互斥、有限离散的元素构成的非空集合，在具体问题中一般由所有可能的决策结果、判断结论等要素构成。其中，Θ的所有子集组成的幂集，记为2Θ，即

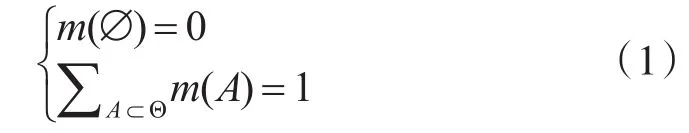
则称函数m为Θ上的质量函数，即基本概率分配函数。m（A）表示对辨识框架Θ中任意子集的分配值，称为基本概率分配（BPA）。

多证据组合规则采用Dempster组合规则［11］，设m1,m2,∙∙∙,mn为辨识框架Θ上的若干证据的BPA，焦元可表达为Ai（1≤i≤n），则其合成规则可表达为

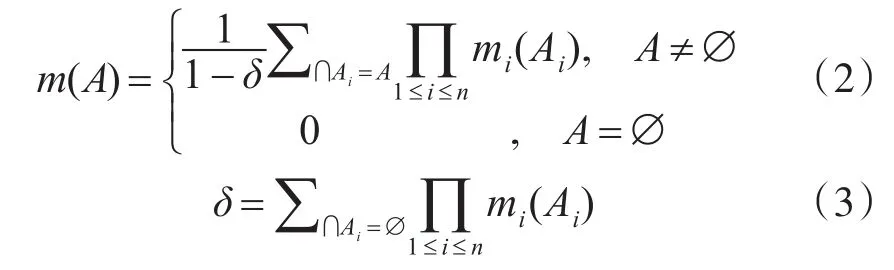
则称δ为冲突因子，反映若干独立证据的冲突程度。易知，当δ=1时，证据内存在完全冲突；当0<δ<1时，为非完全冲突，则Dempster组合规则可用。

该决策模型将多种相关联指标有效融合，较好解决存在冲突证据条件下的多子集可信度融合问题，并通过量化赋值和归一化处理，将冲突按比分配给各个焦元，进而得到各子集置信度。

4.2 AHP法确定指标权重

在两栖作战直升机着陆区选择决策中，除需要对各指标赋值打分外，还需对指标体系中各项指标进行权重对比的衡量，以最终确定最佳着陆区的选择。在指标体系中，运用AHP法通过对比相对决策目标的重要程度，即可确定各指标对决策目标的权重［12］。

第一步，构建判断矩阵与确定相对重要性权重向量。在建立指标模型的基础上，采用专家赋值法对同一隶属关系下且同一层级的各因素进行两两比较，建立判断矩阵MB，则第i个元素Bi相对第j个元素Bj的相对重要性关系为bij。

进而得各元素相对重要性向量ωi为

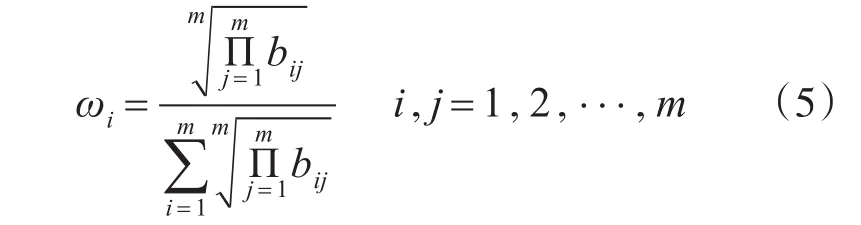
令WB=（ω1，ω2，…，ωm）为相对重要性权重向量。

第二步，一致性检验。对判断矩阵MB的一致性进行检验，检查是否存在逻辑矛盾，确保赋值的逻辑合理性。首先需按照下式计算矩阵MB的最大特征根：

其次，引入一致性指标CI，由下式计算得：

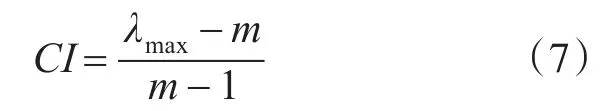
其中，m为矩阵MB的阶数。

进而，得一致性比率：

其中，RI为平均随机一致性指标。一般，CR越小则判断矩阵的一致性越理想，通常认为当CR小于0.1时，判断矩阵具有满意的一致性；反之，则判断矩阵一致性有待修正。

4.3 投影法确定优劣排序

AHP法主要用于指标体系内各指标间的权重衡量，D-S证据理论有效消除了指标间的冲突性问题。据此，在具体选择决策时，可综合二者，运用投影法，获取各着陆区方案指标置信度向量在指标权重向量上的投影，进而通过对比投影大小，即可确定各着陆区方案的优劣排序。

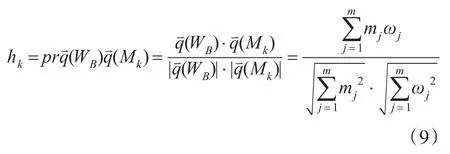
5 着陆区选择实例运用

假设在对某岛的两栖作战中，指挥员在作战筹划中共确定3个直升机着陆区备选方案。运用专家系统评估方法，从战术突然性、敌防御火力部署、着陆区条件和作战协同四方面，对两栖作战的有利程度进行打分，并将专家评分进行归一化处理，结论如表1所示。

表1 着陆点专家评语量化归一值

根据式（3）计算得到δ1=0.924，进一步计算得m1（A）=0.067，m1（B）=0.069，m1（C）=0.381，m1（D）=0.483，即指标质量函数M1为（0.067，0.069，0.381，0.483），是判断该着陆区方案是否为最优着陆区的各指标信任值，其指标体系置信度向量为（0.067，0.069，0.381，0.483）。

同理，根据式（3）计算得到δ2=0.938，进一步计算得m2（A）=0.274，m2（B）=0.183，m2（C）=0.218，m2（D）=0.325，即指标质量函数 M2为（0.274，0.183，0.218，0.325），则指标体系置信度向量为（0.274，0.183，0.218，0.325）。

根据式（3）计算得到δ3=0.924，进一步计算得m3（A）=0.519，m3（B）=0.304，m3（C）=0.052，m3（D）=0.125，即指标质量函数M3为（0.519，0.304，0.052，0.125），则指标体系置信度向量为0.304，0.052，0.125）。

进而运用AHP法对各指标权重进行两两对比分析，得到如表2结果。

根据表2即可构建指标权重判断矩阵，运用式（5）计算可得，各指标的权重向量为WB=（0.359，0.325，0.193，0.123）T，通过式（6）、（7）计算可知，矩阵最大特征根λmax=4.093，一致性比率CR=0.0348<0.1，则有判断矩阵具有满意一致性。即得到各指标相对总体目标的相对重要性权重向量qˉ(WB)=（0.359，0.325，0.193，0.123）。

表2 决策指标相对权重

通过式（9）计算可得，备选着陆区方案的置信度向量在指标权重向量上投影为 h=（h1，h2，h3）=（0.538，0.875，0.940）。则根据投影的优劣排序为h3>h2>h1，易知3号着陆区为最优选择，同时2号着陆区具有较好的综合评价，可选作为备用着陆区。对比运用文献中方法得出的结论，通过综合评价法获取的结论具有较好的吻合度和区分度，有利于决策者作出科学决策。

6 结语

本文运用改进后的D-S证据理论和AHP法结合，建立了针对多属性问题的选择决策模型。通过获取指标置信度向量在指标权重向量上投影大小的方法确定直升机着陆区方案优劣排序。通过案例计算表明，该综合评价法避免了单独使用D-S证据理论和AHP法的局限，在解决两栖作战中着陆区选择决策问题上切实可行，且同样适用于其他多属性多目标决策判断优化问题。此外，应认识到结论的取得受限于模型的合理程度和指标的精细程度，对选择决策的影响指标无法枚举，因此两栖作战中直升机着陆区选择决策模型仍有进一步研究的价值和空间。