混合调制雷达信号识别方法∗

熊 鹏 程志锋

（海军工程大学电子工程学院 武汉 430000）

1 引言

从海湾战争以来的几次局部战争中可以看出，敌对双方争夺电磁频谱使用和控制权的战争愈演愈烈［1］。从海上方向侦察获取常规脉冲雷达信号在雷达信号环境中所占比例逐步减少，复杂调制雷达信号逐渐增多。最常见的复杂调制雷达信号是脉内混合调制雷达信号［2］。脉内混合调制形式主要包含以下几种：频率编码（Frequency Shift Key⁃ing，FSK）、频率编码与线性调频组合（Frequency Shift Keying with Linear Frequency Modulation，FSK-LFM）、频率编码与二相编码组合（Frequency Shift Keying with Bi-Phase Shift Keying，FSK-BPSK）等。

在众多的调制识别方法中，对调制先验信息依赖少、受信号调制参数影响小、运算速度快的识别方法更受研究者青睐。基于瞬时特征识别方法需提取信号的瞬时幅度、无混叠瞬时相位和瞬时频率等信息作为分类依据，比较有代表性的是A.K.Nan⁃di［3］等提出的9个特征参数对超过11种模拟和数字信号调制类型进行分类，但由于瞬时相位和瞬时频率的提取对噪声敏感，因此该方法对信噪比要求较高。基于时频分析法［4］有Wigner-Hough变换法、短时傅里叶变换法（Short-time Fourier Transform，STFT），其中，Wigner-Hough变换［5］多用于检测直线调制信号；STFT运算量大，时域分辨率和频域分辨率无法同时兼顾，会使得时间和频率精度不高。基于高阶累积量［6］的方法虽具有良好的抗噪性，但由于高阶累积量是基于同步采样序列的，对同步技术要求较高。实验表明，以上方法都只适合识别特定调制类型的信号，算法的适用范围有局限性，尤其在分析混合调制雷达信号时，效果不太理想。

本文提出了一种针对混合调制信号的识别方法。本方法首先利用直方图法统计信号的瞬时频率（Instantaneous Frequency，IF），判断信号载频个数，根据载频个数的不同可将重点关注的混合调制信号从复杂电磁环境中筛选出作为一类特殊信号，通过一种改进的滑动平均差分取峰值的方法将复杂信号的识别问题转化为常规信号识别问题，从而大大降低了识别难度。本文提出的方法流程经实验仿真表明，在信噪比较低情况下也能达到较高的识别率。

2 识别算法

本文提出的算法流程围绕混合调制信号的IF特征展开，首先利用直方图统计信号IF值，将混合调制信号筛选出来再次利用IF信息进行分段处理，最后提取混合调制信号分解出的常规信号的IF进行调制识别。

2.1 瞬时频率的提取

本文采用Kay提出的IF估计方法［7］，用窗函数对解卷后的非线性相位序列的差分结果进行平滑，使得对IF的估计效果得到明显改善。Kay方法估计IF可得：

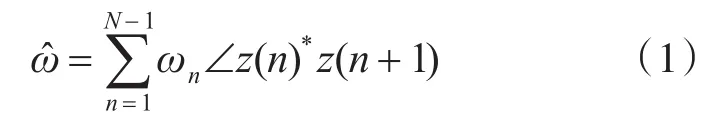
其中窗函数ωn可表示为

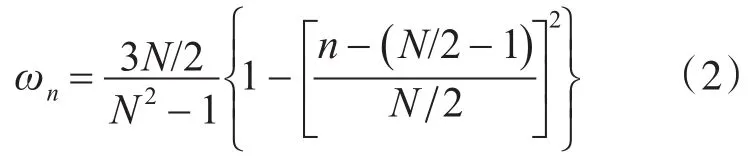
式中N为窗函数长度，n=0:N-1。

2.2 脉冲信号载频个数估计

通常判断信号载频个数的方法有IF结合直方图法、基于Burg模型的AR功率谱估计方法、傅里叶变换法。傅里叶变换法对噪声十分敏感，在较低信噪比条件下，谱峰个数非常不稳定，很难判断出信号载频个数。基于Burg模型的AR功率谱估计方法仅适应脉宽较小的信号，而一般混合调制信号的脉宽较大，此时利用该方法得到的谱图分辨率较差，谱峰之间容易混淆、合并，效果并不理想。

IF结合直方图法是利用直方图对信号的IF值进行统计，此方法对噪声、毛刺等干扰因素不敏感，对信号调制类型、脉宽大小没有特殊的适应性。经过信号预处理阶段后，利用直方图统计平滑后的IF可以较为准确地估计载频个数。

图1为在信噪比为0dB情况下，信号经过预处理阶段后，再通过三种载频估计方法估计包含4段子脉冲的FSK信号效果图，从图1（a）可以看出，频谱图受噪声影响严重，载频个数难以判断准确；图1（b）中的功率谱图的谱峰出现了混淆、合并现象，载频个数也无法判断准确；图1（c）的峰值数目明显，效果最佳。从图1明显可以看出选择IF结合直方图法判断信号载频个数的优越性。

图1 检测信号载频个数效果图

2.3 混合调制信号的识别

混合调制信号主要特点是包含若干个不同载频的子脉冲，且在子脉冲内部进行各自的随机窄带调制，经过大量的对于混合调制信号子脉冲的实验分析，总结得出一般性结论：脉内子脉冲调制形式一致、持续时间相等［8］。换句话说，混合调制信号是若干个持续时间相等、调制形式一致、调制参数相同，中心频率不同的常规调制信号的组合信号［9］。

在本文中我们采用一种改进的滑动平均差分取峰值的方法估计混合调制信号频率跳变位置，即可在频率跳变位置处将混合调制信号切分成常规信号。具体步骤如流程图2所示。

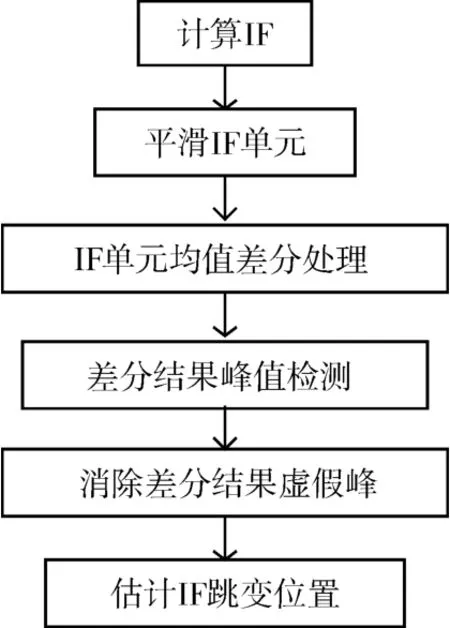
图2 滑动平均差分取峰值法流程图

通过以上切分步骤，可将混合调制信号分解成为若干个常规调制信号，对任意一个子段就可利用常规调制信号识别算法，常规调制信号识别方法十分成熟，国内外在这方面已经做了大量的研究工作［10～12］，因此本文不再赘述。

3 仿真结果

仿真以单载频（Continuous Wave，CW）信号、LFM 信号、BPSK信号、QPSK（Quadrature Phase Shift Keying，QPSK）信号、FSK信号、FSK-LFM信号、FSK-BPSK信号为对象进行。常规信号的中心工作频率f0为50MHz，采样点数为4000；混合调制信号的中心工作频率分别取40MHz～70MHz，每一段采样点数也为4000。采样率fs为500MHz。为了不失一般性，相位编码信号的相位改变、频率编码信号的频率改变完全随机产生。

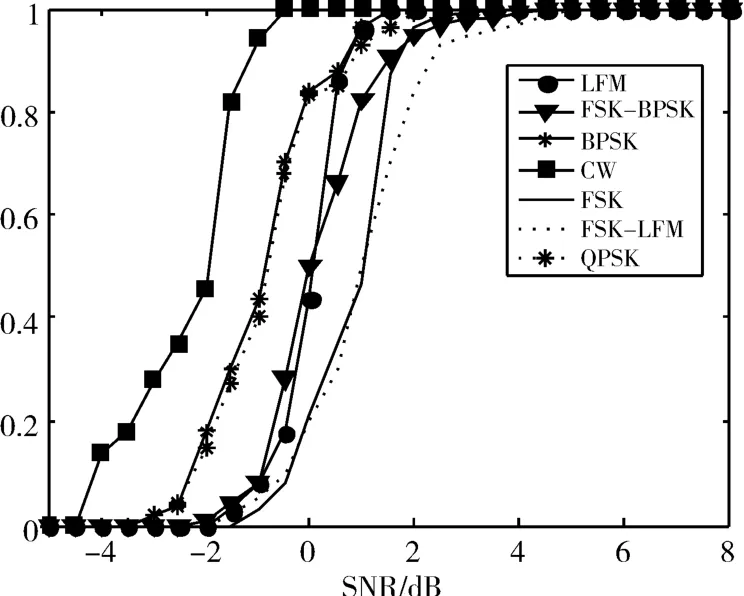
图3 不同信噪比下的识别结果

图3显示了在不同信噪比条件下七种信号通过1000次蒙特卡洛仿真实验得到的识别结果。通过图3的仿真结果可知：1）在信噪比较高条件下，算法具有很高的识别率，在信噪比大于3dB时对以上七种信号的识别率能达到94%；2）带有频率编码的混合调制信号的识别率普遍低于相应不带有频率编码的常规调制信号。这是因为信号受噪声影响，IF特征的提取会出现困难，导致捕捉IF直方图峰值信息的准确性降低，而常规信号的IF特征要求相对混合调制信号的IF特征要求较宽松，具有一定的识别容错性，混合调制信号的IF特征要求十分苛刻，尤其在信噪比较低时，由于IF特征提取困难，信号分段出错可能性增加，导致识别率下降。

4 结语

本文提出了一种主要针对雷达脉内混合调制信号如FSK信号、FSK-LFM信号、FSK-BPSK信号等七种信号的调制形式的识别方法，初步解决了雷达混合调制信号识别分选问题。该算法首先利用直方图统计信号IF将常规信号和混合调制信号进行区分，对于混合调制信号，采用一种改进的滑动平均差分取峰值的方法将混合调制信号分成单段信号，再提取单段信号进行识别。本算法具有计算量小、速度快，识别流程清晰简洁，易于工程应用等特点。仿真实验表明在信噪比大于3dB时算法对以上调制信号具有较高的识别率，具有较强的工程实用性和可行性。