反潜巡逻机对潜应召搜索声呐浮标布放阵位优化问题研究∗

唐 晨 孙秀文 王 旅

（1.海军指挥学院 南京 210016）（2.92771部队 青岛 266400）

1 引言

反潜巡逻机由于机动性强、携带浮标数量多、搜攻潜效率高，正成为现代反潜作战中的重要兵力，并在应召反潜中得到广泛应用。反潜战斗主要包括搜索、跟踪和攻击潜艇，而搜索发现潜艇是实施反潜战斗的首要环节［1］。因此，研究对潜应召搜索中声呐浮标优化阵位以尽可能发现拦截潜艇具有十分重要的现实意义。

2 反潜巡逻机对潜应召搜索声呐浮标布放阵位一般模型及其不足

2.1 一般模型

应召反潜是指反潜兵力根据上级指示或其他兵力召唤，前往发现潜艇的海区实施反潜的方式［2～5］。反潜巡逻机布放的声呐浮标要尽可能地包围潜艇扩散区域，一般外切于潜艇扩散圆或者半圆［6～7］。其中，当潜艇的规避航向可以判定不超过180°时，外切于潜艇扩散半圆；当潜艇的规避航向无法确定时，外切于潜艇扩散圆。这里以潜艇的规避航向不超过180°为例进行分析，其他情况与之分析类似。

潜艇的扩散半径［8～9］（R潜），通常与潜艇可能的规避速度（v潜）、延误时间［10～11］（t延误）、反潜巡逻机布放声呐浮标的时间（t布放）有关。通过分析，不难发现关系式为

图1 声呐浮标一般阵位示意图

如图1所示，声呐浮标阵的长度为4R潜。已知反潜巡逻机布放声呐浮标的速度（v飞机），可得：

由式（1）、（2），可得：

其中，t延误=t报告+t决心+t机动。t报告为与潜艇失去接触至上级指挥所接到报告的时间；t决心为上级指挥所接到报告至定下决心的时间；t机动为上级指挥所定下决心至反潜巡逻机抵达搜索海域的时间。

已知声呐浮标之间的布放间隔（d间隔），需要的声呐浮标的数量（n）为

2.2 存在不足

反潜巡逻机按上述模型布放声呐浮标，虽然从理论上也能满足作战需要，但是使用的声呐浮标数量过多，不利于节约用兵。并且由于反潜巡逻机携带的声呐浮标数量总是有限的，当潜艇规避速度较大或者延误时间稍长时，潜艇的扩散范围会非常大，可能会出现声呐浮标不够的情况，甚至导致应召搜索的失败。因此，保证对潜艇有效拦截的情况下，应对声呐浮标的布放阵位进行优化。

3 反潜巡逻机对潜应召搜索声呐浮标布放阵位模型分析与优化

3.1 模型原理［12］描述

这里同样以潜艇的规避航向不超过180°为例进行分析，其他情况与之分析类似。不难发现：潜艇以规避速度定向机动，扩散范围最大。因此，声呐浮标要包围该区域。不妨假设潜艇定向定速规避。为便于描述，潜艇的位置用极坐标（r，θ）表示，并分析判断得出了潜艇的规避速度（v潜）。如图2所示，潜艇的丢失位置点为O点，最有可能的规避航向在（0，180°）之间。假设潜艇初始规避航向是那么反潜巡逻机最佳搜索策略应是与潜艇相向而行。通过计算，预计两者相遇点在A点，于是反潜巡逻机在A点布放声呐浮标探测。若未发现潜艇，则判定潜艇航向不是此时，潜艇应该在以O点为圆心、OA为半径的圆上。下步，可以将潜艇航向增加一个非常小的角度dθ，认为潜艇沿着方向规避。反潜巡逻机则从A点赶赴预计与潜艇相遇的B点，布放声呐浮标探测。若仍未发现潜艇，则判定潜艇航向不是此时，潜艇应该在以O点为圆心、OB为半径的圆上。下步，可以将潜艇航向再增加一个dθ，认为潜艇沿着方向规避。反潜巡逻机则从B点赶赴预计与潜艇相遇的C点，布放声呐浮标探测。若仍未发现潜艇，则继续按上述方法布放声呐浮标探测。理论上，在（0，180°）范围内总会在某个点探测到潜艇。

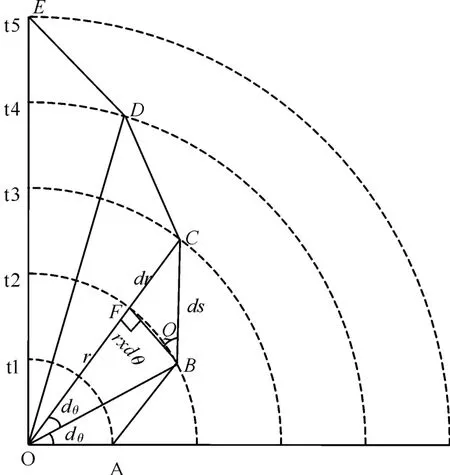
图2 反潜巡逻机搜索潜艇示意图

3.2 建立模型

根据上述描述，可以建立微分方程，计算得出反潜巡逻机声呐浮标布放阵位。如图2所示，不妨假设反潜巡逻机在B点未发现潜艇，而在C点发现潜艇。由于dθ非常小，可以近似认为∠OFB为直角。那么在ΔBCF中，有

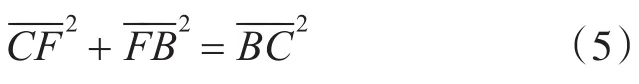
根据潜艇与反潜巡逻机的运动路径和几何关系，可知

其中，dr、ds分别为潜艇与反潜巡逻机的航程微分。由式（5）、（6）、（7）、（8），可得：

同时，由于潜艇从F点航行至C点的时间与反潜巡逻机从B点飞行至C点的时间相等，可得：

由式（9）、（10），可以计算得出反潜巡逻机声呐浮标布放阵位在极坐标中的方程为

令θ=0，可得：

其中，R开始为反潜巡逻机开始布放声呐浮标的位置点。由式（11）、（12），可得：

由式（13），可知声呐浮标的最优化阵位应该为一条对数螺线。但是在实际中，反潜巡逻机不可能按照螺线作出相应的机动。因此，需要对反潜巡逻机声呐浮标布放阵位进行适当调整。

3.3 模型优化

反潜巡逻机声呐浮标布放阵位选择的要求主要有：一是声呐浮标要能够尽可能地包围潜艇可能的扩散范围，防止潜艇逃脱；二是布放声呐浮标的路径要能满足反潜巡逻机的机动要求；三是尽可能少地使用声呐浮标，节约兵力器材。据此，为便于作战运用，反潜巡逻机可以选择外切螺线的扩方路径布放声呐浮标。

为便于描述反潜巡逻机的布放航向和转向点，下面用直角坐标系表示。在直角坐标系中，螺线上点的坐标，可以用下面这个方程组进行变换。

因此，螺线上各点切线的斜率为

为能够较好地满足声呐浮标布放阵位选择要求，如图3所示，反潜巡逻机开始布放声呐浮标的位置点可以由A点调整到B点，采取的航向为尔后在D点转向，采取的航向为最后在F点转向，采取的航向为其中，与x轴垂直，与螺线相切于C点；与x轴平行，与螺线相切于E点；与x轴垂直，与螺线、x轴共同相交于G点。

图3 声呐浮标优化阵位图

解得θ=Q。因此，由式（14），C点的坐标为

由式（14）和θ=π，可知 G点的坐标为

至此，就得出了反潜巡逻机声呐浮标布放阵位B点、D点、F点、G点等关键坐标的计算公式。

声呐浮标阵的总长度（L）为

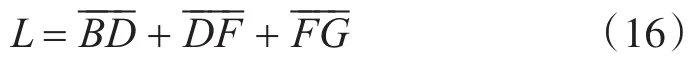
需要的声呐浮标的数量（n）为

4 仿真验证

下面，通过仿真计算，验证潜艇分别采取低速和高速规避时，反潜巡逻机运用一般模型和优化模型布放声呐浮标的可行性。设定的相关参数、数据如表1所示。

表1 设定数据表

情况1：潜艇的规避速度为10节

反潜巡逻机运用一般模型布放声呐浮标阵。由式（3），潜艇的扩散半径为12.3km；由式（4），声呐浮标阵的总长度为49.2km，需要的声呐浮标数量为14枚。反潜巡逻机运用优化模型布放声呐浮标阵。由式（16），声呐浮标阵的总长度为37.1km；由式（17），需要的声呐浮标数量为11枚。优化模型比一般模型节约3枚声呐浮标。

情况2：潜艇的规避速度为25节

反潜巡逻机运用一般模型布放声呐浮标阵。由式（3），潜艇的扩散半径为60.5km；由式（4），声呐浮标阵的总长度为242.0km，需要的声呐浮标数量为62枚。反潜巡逻机运用优化模型布放声呐浮标阵。由式（16），声呐浮标阵的总长度为92.7km；由式（17），需要的声呐浮标数量为25枚。优化模型比一般模型节约37枚声呐浮标。

通过仿真计算结果可以发现：当潜艇的规避速度为10节、速度较低时，反潜巡逻机运用优化模型比一般模型节约声呐浮标数有限，但当潜艇的规避速度达到25节、速度较高时，反潜巡逻机运用优化模型比一般模型能节约大量声呐浮标。因此，在实际运用中，当潜艇采取低速规避时，仍可以运用一般模型布放声呐浮标，但当潜艇高速规避时，应该优先运用优化模型布放声呐浮标。

5 结语

这里研究的声呐浮标阵位是基于矩形或正方形的阵位。因此，仍然是比较优化的阵位，还不是最优化的阵位，对于最优化的阵位还需要后续进一步研究讨论。同时，对潜应召搜索通常需要多兵种协同完成，对于协同兵力在声呐浮标阵包围区域或开口区域如何搜潜的问题，还需要后续研究分析。