基于质量评价最优的无人机航拍图像去雾方法

2022-03-14姜雨彤宋海平王光辉

兵工学报 2022年1期

姜雨彤，宋海平，王光辉

(中国北方车辆研究所，北京 100072)

0 引言

图像去雾方法是近年的研究热点，基于大气散射模型的图像去雾方法得到了大力发展，但是无人机航拍图像去雾仍然是尚未解决的难题。近年来，无人机航拍作为新生的观测手段，正在日益走向成熟，从而对无人机图像的去雾方法及去雾效率提出了更高的要求。

传统的无人机采用装载一个固定图像传感器从上往下垂直摄影(见图1(a))。为提高无人机影像采集的灵活性，装载一个可调节角度相机，可实现多角度倾斜摄影(见图1(b))。随着倾斜摄影技术在国际测绘遥感领域的迅速发展，通过在同一无人机平台上搭载五摄像机(见图1(c))，可同时从垂直、倾斜等不同角度采集影像。如图2所示，机载五摄像机组可获取地面场景多个方位图像，并可供用户多角度浏览，使地面场景的影像信息更为完整。

图1 无人机机载摄像机示意图Fig.1 Schematic diagram of UAV-borne camera

图2 无人机机载五摄像机影像获取示意图Fig.2 Schematic diagram of five-camera image acquisition on UAV

图3 无人机垂直摄影图像Fig.3 UAV vertical photographic image

当无人机图像传感器从高空向地面垂直向下摄影时(见图3)，获取的图像上所有场景点的深度几乎一致并等于飞行高度。而且由于飞行高度大多在几百米或上千米，地物的高度差可以忽略不计。因此，场景透射率差别不大，各景物受雾影响的程度大体相同。另外，此类无人机图像几乎不存在天空区域，现有的估计大气光的方法往往存在误差，致使去雾图像存在不同程度的色移。针对无人机航拍图像的应用背景，不仅需要清晰化去雾处理，还要求图像去雾算法复杂度较低、处理速度较快，为无人机图像去雾后的信息处理作重要预处理工作，争取有利时间。

因此，需要研究一个计算复杂度低、去雾效果好的去雾模型，降低去雾计算复杂度，可更好地实现处理的图像去雾方法。针对无人机正拍图像的特殊性，不需考虑整幅图像雾气浓度随景深的变化，只需简化图像去雾过程，研究出针对无人机正拍图像去雾适用性强、执行效率高的去雾方法。

常见的图像去雾算法可以分为3类，基于物理先验模型的方法，基于图像增强的方法，以及使用深度学习的方法。然而这些方法通常用于处理地面平视雾天图像且计算复杂度高，未能充分利用无人机航拍图像所有场景点具有近似光学深度这一有利先验条件。

为了探索一种计算复杂度低的图像去雾方法，本文提出一种基于质量评价最优的无人机图像去雾方法。针对高空垂直拍摄所获取的无人机正拍图像，研究图像质量评价参数，建立图像质量评价函数，在此基础上选择图像质量评价函数值最优的图像作为去雾结果，实现无人机正拍图像的高效去雾处理。

1 无人机图像去雾原理

无人机正拍图像，相对于无人机斜拍图像和普通景物图像，有着自身的特点。当无人机上的相机从几百米或上千米高空垂直向下拍摄时，视野内场景点到达无人机上相机的距离近似一致，地物的高度差可忽略不计，场景中各景物受雾气影响的程度大体相同。

对于有雾场景的描述通常使用简化的大气散射模型，该模型将有雾图像描述为清晰无雾图像与大气光在不同场景点处以不同比例进行叠加，大气散射模型数学上可以表示为(1)式，

(，)=(，)+(1-)，

(1)

式中：(，)、(，)分别表示有雾图像以及原始无雾图像的像素点灰度值，(，)为像素点坐标；为全局的大气光值，表示无穷远处背景光的多少；为大气透射率，表示叠加大气光的程度值，该比例与场景点的深度值相关，

=e-，

(2)

为固定的大气散射系数值，为场景点的深度。

由于大致相同，对单幅图像可以将作为全局值进行处理，从而得到更精简的大气散射模型如(3)式：

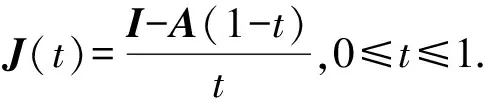
(3)

本文将普通图像去雾求解整幅图像所有像素点透射率图的问题转变为求解整幅图像全局透射率值问题，大幅度降低无人机正拍图像去雾算法的计算复杂度，可以更好地实现无人机图像的去雾处理。

本文结合信息熵(IE)、标准差(SD)和图像傅里叶振幅(FA)3种图像质量评价参数展开研究，建立图像质量评价函数(()，()，())，()、()、()分别为图像的IE、SD、FA在此基础上提出基于图像质量评价最优(OIQE)的去雾方法。若输入有雾图像，且大气光已知，则将透射率作为大气散射模型的唯一自变量参数，通过对透射率的不同取值，可根据(3)式求解出不同的去雾图像。

将各去雾图像代入图像质量评价函数中，求取最优值即质量评价函数的最大值，根据(4)式将所获得的图像确定为去雾结果，

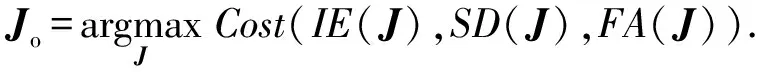
(4)

2 无人机图像质量评价参数

无人机图像常作为军事侦察、毁伤评估、国土监测和灾害救援的重要信息来源。因此对无人机图像的去雾结果提出了包含信息量大、对比度高、细节恢复程度高、纹理清晰和边缘特征明显等要求。IE是表示图像信息丰富程度的重要指标，从信息论角度出发，反映了图像信息的多少；SD是表示像素点离散程度的重要指标，是反映图像各像素灰度值分布程度；图像的FA是表示场景中物体边缘变化幅度大小的重要指标，是反映构像纹理的清晰程度。因此，本文采用IE、SD、图像FA来综合定量评价去雾后图像的质量。

2.1 图像IE求解

IE是图像中所含信息量的度量指标，表征图像灰度分布的聚集特性，在图像中，当各个灰度级出现的概率相等时熵最大。根据这个理论，图像的值越大，表明其包含信息量越大，即图像细节纹理信息较丰富；图像的值越小，表明其包含信息量越小，即图像细节纹理信息较匮乏。图像IE的表达式为

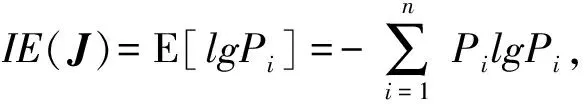
(5)

式中：表示图像所含的灰度级总数(1≤≤256)；表示第级灰度在图像中出现的概率大小，此概率可由灰度直方图统计获得。

可将图像IE作为参数，来评价去雾图像的质量。如果去雾图像的IE增大，则说明去雾处理后图像所包含信息量超过了未经处理的有雾图像，有效地去除雾气对图像的影响，恢复图像所包含的细节纹理。也就是说去雾后图像的IE越大，就越有可能复原图像中的信息量，越接近无雾时的真实场景图像复原。由于无人机图像是获取视觉信息的主要来源，它所包含信息量的大小直接影响其利用价值，因此IE可作为评价无人机图像去雾结果好坏的重要参数。

2.2 图像SD求解

SD用于度量图像的对比度，其值的大小直接反映了图像的清晰程度。图像的SD值越大，表明图像的灰度值在整个灰度阶范围内离散性越好，有着较高的对比度和较好的色彩表现，最终说明该检测图像清晰度越高；相反，如果SD值越小，表明图像灰度值过于集中，有着较低的对比度和较差的色彩表现，最终得出图像清晰度越低。图像SD的表达式为

(6)

式中：、分别为图像的宽和高；为图像像素灰度的平均值。

图像SD也可作为评价去雾图像质量的参数。如果去雾图像的SD显著增大，则说明去雾处理使图像灰度的离散性增大，恢复了图像的对比度，使去雾图像的清晰程度大大超过未经处理的有雾图像，并有效地去除雾气对图像的影响。也就是说去雾后图像的SD越大，就越接近无雾时的真实场景图像复原，因此对于无人机图像来说，SD可作为评价无人机图像去雾结果好坏的重要参数。

2.3 图像的FA谱

傅里叶变换可以看作一个玻璃棱镜，可将一束光分解为不同颜色的光，而每个颜色的光则取决于波长(或频率)。傅里叶变换可作为数学上的棱镜，将函数分解为不同频率的成分，当分解对象为光时，则是由光谱或频率谱所决定的。由于傅立叶变换是通过频率成分来分析一个函数的，它也是实现线性系统分析的一个有力工具，可为解决图像处理问题提供思路，利用频域中特有的性质，使得许多图像处理过程更加简单、有效。傅立叶变换是将图像从空间域转换到频率域，其物理意义是将图像的灰度分布函数变换为图像的频率分布函数。对于二维图像信号(，)，其傅里叶变换定义为

(7)

式中：=0，1，2，…，-1；=0，1，2，…，-1

由于FA的动态范围往往过大，通常作如下对数变换：

(,)=lg[1+|(,)|]，

(8)

式中：(·)为变换后的FA；为比例常数。

图像的FA也可作为评价去雾图像质量的重要参数。如果去雾图像的FA值增大，则说明去雾处理使图像相邻像素的变化很剧烈，恢复了图像的尖锐度，使去雾处理后图像的清晰程度大大超过未经处理的有雾图像，有效地去除雾气对图像的模糊。也就是说去雾后图像的振幅值越大，就越接近无雾时的真实场景图像复原，因此对于无人机图像，图像的FA可作为评价无人机图像去雾结果好坏的重要参数。

3 图像质量评价函数的建立

选定IE、SD、FA作为去雾图像质量的评价参数，三者的值越大，说明去雾后的图像质量越高，去雾处理算法越有效。表1所示为雾天图像及其候选去雾图像。求取候选去雾图像的IE、SD、FA谱，以最大IE值或最大SD值或最大FA中值所对应的图像作为最优去雾结果。表2给出了候选去雾图像1、2、3、4、5、6、7、8的IE、SD、FA中值具体求取结果，分别标记出各参数最大值。

为了进一步比较3个参数的计算结果，图4给出了IF、SD、FA计算值的曲线图，并标注了它们各自最大值的取值位置。由图4可见：候选去雾图像5号的IE最大，被选定为以IE为评价标准的去雾结果；相对于雾天图像，被雾气覆盖的细节纹理信息被恢复，但图像并未完全去除雾气的笼罩，仍有部分区域未能去雾彻底。候选去雾图像4号的SD最大，被选定为以SD为评价标准的去雾结果；相对于雾天图像，图像的对比度大幅度提高了，但部分区域去雾过度，使细节纹理信息被模糊。候选去雾图像3号FA的中值最大，被选定为以FA为评价标准的去雾结果；相对于图雾天图像，图像的边缘更明显，但图像整体色调偏暗，出现了过饱和现象。由此可见，IE、SD、FA这些参数分别单独作为去雾图像质量的评价指标通常无法得到一致性的结果，是一个亟待解决的问题。

表1 雾天图像及其候选去雾图像

表2 候选去雾图像的IE、SD、FA中值的计算结果

图4 候选去雾图像IE、SD、FA中值计算结果及其最大值Fig.4 Calculated results of candidate dehazed image information entropy，standard deviation，Fourier amplitude median and their maximum values

为了弥补单一去雾图像质量评价参数的片面性，则将IE、SD、FA 3个质量评价参数相结合，建立一个更全面、更合理的质量评价函数，表达式为

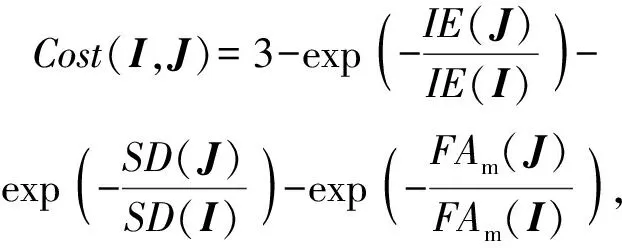
(9)

式中：()、()、()为雾天图像所求得的IE、SD、FA中值；()、()、()分别为根据雾天图像所获得的去雾图像所求得的IE、SD、FA中值。()、()、()的值比()、()、()提高得越大，(，)的值越大，说明去雾图像的质量越高，去雾效果越好。

由于雾气的存在会使图片的IE、SD以及FA 3个图像指标减小，对于雾天图像，当()、()、()固定时，其3个指标的值越大，去雾图像的去雾效果越好。质量评价函数的值与去雾图像的3个指标值均呈正比，通过函数可将3个指标进行联合，并将综合评价分数限制在[0，3]范围。

4 无人机图像去雾算法

本文提出的OIQE方法主要分为以下4个步骤：1)对进行粗略取值，获取初步候选去雾图像；2)采用质量评价函数，计算各初步候选去雾图像的质量评价值，选取最大值所对应的候选去雾图像，作为初步估计结果；3)提取初步确定的去雾结果所对应的值，根据的小范围取值获得一系列精确候选去雾图像；4)采用质量评价函数，计算各精确候选去雾图像的质量评价值，并选取最大值所对应的候选去雾图像，作为最优去雾结果图像。

大气光值表示无穷远处背景光的大小，在有天空的场景中通常可以采用远处天空的灰度值，很多基于大气散射模型的去雾方法对大气光的求解进行了简化。例如暗通道方法将大气光值取为前1亮度点处的灰度，Kim等的去雾算法不断对图像进行四叉分割，并每次均选取平均灰度最大的一块，但是无论哪一种方法都受到场景中可能存在的白色物体影响，导致大气光估计存在偏差。由于大气光值的计算不在本文的重点研究范围，通过对多个视觉上有雾场景的大气光进行估计后，发现大气光值集中于190以上，因此选取经验值200作为大气光(这里如果需要进一步说明，则需要统计多幅有雾图像)。虽然与实际会产生偏差，但是由于将传输函数作为全局值进行估计，最终的估计也会相应主动地在估计过程中与实际值产生偏差来保证图像的最终质量评价分数仍然最高。图5给出了一幅雾天无人机图像。

图5 雾天无人机图像Fig.5 Foggy UAV image

以图5为例，本文提出的去雾方法具体实现步骤描述如下：

根据(3)式，在雾天图像作为仅有的输入条件时，对取值为=[200，200，200](的取值对本文提出的算法影响并不大，为了简化去雾过程，本文将取值为固定值)，再对唯一的未知数(0≤≤1)进行粗略取值，=[01，01，09]，从01～09变化步长为01取值，通过的这9个取值，可求得相对应的9幅初步候选的去雾图像，如表3所示。可见通过人眼的视觉感受无法准确地判断9幅初步候选去雾图像中哪幅具有最优的质量参数，需要进行步骤2的判断。

表3 不同t取值所对应的初步候选去雾图像

先根据(6)式计算雾天图像(见图5)的()，以及9幅初步候选去雾图像(见表3)的(1)、(2)、(3)、(4)、(5)、(6)、(7)、(8)、(9)；再根据(7)式计算雾天图像(见图5)的()，以及9幅初步候选去雾图像(见表3)的(1)、(2)、(3)、(4)、(5)、(6)、(7)、(8)、(9)；接下来根据(9)式计算图像的，从而将所有像素点的FA中值代表雾天图像(见图5)的()，以及9幅初步候选去雾图像(见表3)的(1)、(2)、(3)、(4)、(5)、(6)、(7)、(8)、(9)；然后将计算所的值代入(9)式质量评价函数，并求得9幅图像相对应的质量评价参数值(，1)、(，2)、(，3)、(，4)、(，5)、(，6)、(，7)、(，8)、(，9)；最后在9个质量评价参数其中选择最大值，并将其所对应的初步候选去雾图像作为初步去雾结果图像，其所对应的值作为初步透射率结果，表达式为

(10)

式中：=[01,01,09]。

图6所示为根据表3的9幅初步候选去雾图像所求得的质量评价参数值曲线，可见在6号图像处取得最大值，则图像6被确定为初步去雾结果图像，它由=06确定得到。

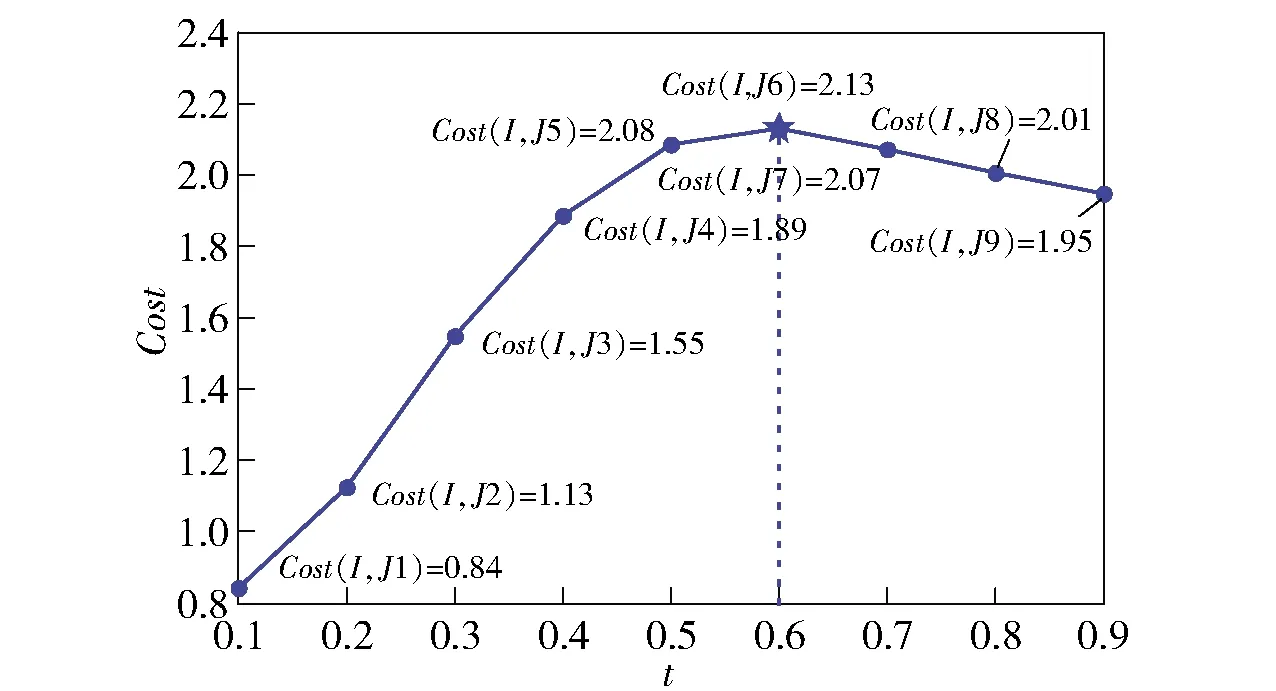
图6 不同t值对应的初步候选去雾图像质量评价参数值及最大值Fig.6 Quality evaluation parameter values and maximum values of initial candidate dehazed images corresponding to different t values

根据步骤2已经初步确定透射率，进一步缩小的取值范围，目的是获得更为精确的透射率将的取值定为=[-01，001，+01]，将的21个取值代入(3)式，可求得相对应的21幅精确候选的去雾图像。这样先粗略取值再精细取值的目的，是在保证取值精度的条件下减少计算量，有效且有针对性地进行去雾处理，保证图像去雾的计算复杂度。如表4所示，通过步骤2求得=06，缩小的取值范围后，将的取值定为=[05，001，06]，可见求得的精确候选去雾图像差别很小，更逼近真实结果。

4) 表4所示21幅精确候选去雾图像，无法通过人眼来判断最优去雾结果。因此，根据(5)式、(6)式、(8)式计算此21幅精确候选去雾图像的IE、SD、FA，代入(9)式求得质量评价参数。比较这21个质量评价参数值的大小，选择其中最大值，并将其所对应的精确候选去雾图像确定为最终的去雾结果图像，其所对应的值作为最终的透射率结果，表达式为

(11)

式中：=[-01, 001,+01]。

如图7所示，此图为根据表4的21幅精确候选去雾图像所求得的质量评价参数值曲线，可见在=056时求得的去雾图像质量参数最大，所以将它所对应的图像(见表4)确定为精确去雾结果图像

通过以上4个步骤即可完成本文提出的无人机图像去雾处理，实现最终去雾图像结果细节信息恢复完整、对比度高、边缘清晰。采用先对粗略取值，再对初步确定的值进行小范围精确取值的方法，大大减少了计算量，实现了有针对性、有效率的去雾处理。

5 无人机图像去雾实验结果及分析

5.1 无人机图像去雾效果评价

选取一组青岛市2014年世园会建设过程中的航拍图像作为一实例，采用本文提出的OIQE去雾方法进行无人机航拍雾天图像的去雾处理实验，如表5所示。由表5可见，去雾后的图像细节信息一目了然、对比度高、边缘清晰，说明OIQE去雾方法可有效去除无人机图像中的雾气干扰，而且可恢复出高质量的清晰图像。

为了证明OIQE去雾方法的优势，首先将其与经典的暗通道先验(DCP)去雾方法进行比较。

表4 不同t取值所对应的精确候选去雾图像

图7 不同t值对应的精确候选去雾图像质量评价参数值及最大值Fig.7 Quality evaluation parameter values and maximum values of accurate candidate dehazed images corresponding to different t values

如表6所示，OIQE去雾方法与DCP去雾方法同时处理一组无人机雾天图像，可见采用OIQE去雾方法处理后所得到的去雾结果相对于DCP去雾方法所得到的去雾结果细节更加清晰，对比度更高。DCP方法得出的去雾图像去雾不完全，雾气仍有残留，并未彻底去除雾气的笼罩。可见所提出的OIQE去雾方法对于无人机图像去雾的实现效果要优于DCP去雾方法。

OIQE去雾方法与目前计算量最小、执行最有效的景深线性估计模型(LMD)去雾方法进行比较。如表7所示，OIQE去雾方法与LMD去雾方法同时处理一组图像，可见OIQE去雾方法处理后所得去雾结果相对于LMD去雾方法所得到的去雾

表5 一组雾天无人机图像及采用本文方法获得的去雾图像

表6 一组雾天无人机图像DCP、OIQE方法去雾结果比较Tab.6 Comparison of dehazed results of a set of foggy UAV images obtained by DCP and OIQE methods

结果细节更清晰，边缘更明确。LMD去雾方法得出的去雾图像纹理模糊，细节被平滑，使图像本来的信息被损失。可见本文OIQE去雾方法对于无人机图像去雾的实现效果要优于LMD去雾方法。

5.2 无人机图像去雾误差评价

为了客观定量地评估提出的OIQE图像去雾方法的性能，采用计算均方差(MSE)的方式对通过无雾图像所合成的有雾图像进行统计，比较OIQE去雾方法与DCP去雾方法和LMD去雾方法所得MSE的大小。

表7 一组雾天无人机图像LMD、OIQE方法去雾结果比较

为了计算雾天图像通过去雾处理方法所获得的去雾结果图像与无雾真实图像的MSE，必须要有同一场景在晴朗天气下的无雾图像做为真值，雾天图像进行去雾处理后的结果图像作为测量值，再进行真值与测量值的误差计算。但实际情况是，很难同时获得同一场景下的真实雾天图像与无雾图像。为了解决这一问题，只能根据(1)式，再给定值和值对无雾图像进行合成有雾图像，然后对合成有雾图像进行处理，计算去雾结果图像与无雾图像的MSE

设=[200，200，200]，=08，04，02，这3个不同的值使每一幅无雾图像都分别获得3幅雾气浓度不同的有雾图像，如表8所示。

表8 一组无人机在晴朗天气下拍摄无雾图像所合成的有雾图像

将得到的合成有雾图像分别采用提出的OIQE去雾方法、DCP去雾方法、LMD去雾方法进行有雾图像去雾处理实验，得到去雾结果图像，并统计其MSE值。为了更有效地展示比较结果，其中=02所合成的有雾图像去雾结果分别与表8中无雾图像真值计算得到MSE结果，如表9所示。

表9 t=0.2时合成有雾图像的不同方法去雾结果和MSE结果

为有效衡量DCP、LMD以及OIQE方法去雾后的图像质量采用IE以及对比度两个无参考指标进行比较，其中IE的计算如(5)式，分别对3个颜色通道应用该公式并最终取均值作为图像的熵。

对比度的计算采用文献[16]中的全局对比度计算方法，该方法将图像进行多次下采样分别计算不同分辨率下的对比度值，然后使用主观实验确定多个对比度值的权重系数，在评价结果上与人眼感受相关性大。对于不同指标使用相同权重的问题，不同权重下的评价函数分值肯定会不同，按照奥卡姆剃刀原理，多组合选择中采用相同的权重较为简便与高效。

表9给出了在=02时合成有雾图像的不同方法去雾结果、MSE结果以及IE和对比度的质量评价比较结果。通过对上述3个指标的计算可以看出，OIQE方法在3个样例场景中的去雾结果均优于DCP方法和LMD方法，充分保留了视觉信息和对比度信息，客观地说明了本节提出的OIQE图像去雾方法对正拍的雾天无人机图像去雾处理的准确性高、计算误差小。