动态加载下高聚物粘结炸药中椭圆孔洞坍塌引起的热点温度及其半经验解析表达

刘纯， 欧卓成， 段卓平， 黄风雷

(北京理工大学 机电学院, 北京 100081)

0 引言

非均质固体炸药在工业和军事领域应用广泛，其安全性一直是研究重点。因此，正确认识炸药中热点的形成和合理描述冲击起爆机理，对高能炸药的安全性具有重要意义。事实上，对于高能炸药，尤其是像高聚物粘结炸药(PBX)的冲击起爆,基本上是由缺陷处形成的局部热点引起的。到目前为止，人们认为有孔洞坍塌、剪切带与晶体的位错运动、晶粒之间的界面摩擦或闭合裂纹等多种机制可以产生热点，其中孔洞坍塌形成热点被认为是主要的冲击起爆机制。

孔洞坍塌形成热点通常以局部温升为特征，是由不同的局部能量沉积机制所所致，主要包括气体绝热压缩、塑性功和射流冲击。然而,应该强调的是,上述所有的能量沉积机制都发生在很小的时空尺度上,并且由于缺少超高速时间分辨率的局部测温技术，使得很难以实验的方法研究孔洞坍塌和热点的形成过程。最近，一些学者对含能材料中的大孔洞(主要是毫米级尺寸的孔洞)在激波作用下孔隙坍塌进行了实验研究和数值模拟,模拟结果与实验结果吻合较好。但上述实验研究针对的是大孔洞，对动载下微米级孔洞的坍塌过程很难进行实验研究，还需要进一步发展。

数值模拟成为一个能够有效阐明孔洞坍塌期间能量沉积细节的研究方法。早期，中尺度模拟被广泛开展，用来研究炸药中球形孔洞坍塌以及热点的形成过程。Tran等分别研究冲击加载下惰性奥克托今(HMX)基质和反应性HMX基质中孔洞的坍塌与演化以及热点的形成过程，得到了从塑性功到射流冲击的各种局部能量沉积机制，并发现射流冲击是内部能量增加的主要原因。Michael等在惰性和反应性模拟中进一步研究了孔洞坍塌过程中温度场的演变，结果发现，热点温度比炸药受冲击后的整体温度高两倍以上，从而在热点处发生点火。Kapahi等研究了孔洞相互作用对热点形成的影响，并且观察到孔洞相对位置会对能量分布和温度升高产生重要影响。最近，一些学者采用中尺度模拟研究了孔洞形态对热点形成的影响，并且发现某些孔洞形态会比其他形态产生更高强度的热点。如Tran等研究了三角形孔洞，并将其行为与HMX晶体中的球形孔洞进行比较，结果表明，与球形孔洞相比，三角形孔洞将导致强度更高的热点，这表明三角形孔洞的存在可能会使炸药更敏感。Levesque等继续研究了孔洞形态(如球形、圆柱形、椭圆形和锥形)对激波后热点温度分布的影响，结果表明，在相同的激波强度和孔洞体积下，椭圆孔洞、圆锥形孔洞和圆柱形孔洞(当它们的最长半径尺寸与冲击波的传播方向一致时)产生的热点都比球形孔洞强得多。此外，Rai等分析了具有成像细观结构的非均质固体炸药的冲击响应行为，并将细长孔洞的方向与初始灵敏度相关联，结果表明炸药的冲击起爆灵敏度在很大程度上取决于细长孔洞的方向以及孔洞的长宽比。

综上所述，动态加载下非均质固体炸药孔洞坍塌形成热点的基本机理方面已经取得了一些进展，然而，由于问题的复杂性和影响因素的多样性，以往的研究只考虑了少数具有独立形状或大小的孔洞的影响，很难得到热点温度关于激波强度、孔洞尺寸以及孔洞构型之间的函数关系。考虑到目前大多数冲击起爆反应速率模型是宏观的和经验的，很难反映细观结构对非均质固体炸药冲击点火的影响，并且从理论上讲，宏观反应是由细观反应演化而来的，有必要构建中尺度下的热点点火反应速率模型。对此，获得热点的本征函数(即一个描述热点温度与冲击强度和孔洞形态关系的具体函数)显得至关重要。

本文的目的是通过理论和数值方法详细地研究在冲击载荷作用下非均质固体炸药内部椭圆形孔洞的动态塌陷以及热点形成过程。通过分析冲击强度和孔洞几何形状(如尺寸、伸长状态和位置)对热点温度的影响，提出一种半经验解析表达式来表征热点温度关于冲击强度和椭圆形孔洞几何形状的依赖关系，为构建中尺度下的热点点火反应速率模型奠定一定的基础。

1 孔洞坍塌形成热点的相似分析

动态加载下非均质固体炸药内部椭圆孔洞坍塌问题如图1所示。在边界冲击载荷作用下，炸药左端产生的激波由左向右在炸药中传播，并在某一点与孔洞(和为椭圆孔洞的两个半主轴长度，′和为椭圆孔洞质心和倾角)发生相互作用，孔洞坍塌从而形成热点。本文将通过相似理论逐步分析在动态载荷作用下孔洞坍塌引起的热点温度与各因素的关系。将最大热点温度(简称热点温度)表示为=+Δ，为初始温度，Δ为热点温升。

图1 动载荷作用下的椭圆孔洞坍塌示意图Fig.1 Schematic diagram of elliptical void collapse under dynamic loading

当PBX受到冲击加载后，炸药内部孔洞在载荷作用下发生坍塌，造成局部温度升高。显然，热点温升Δ取决于外部冲击强度、炸药本身的物理性质和椭圆孔洞的几何性质(如横截面积、位置和伸长状态)。因此热点温升Δ可以写为

Δ=(,,,,,,,,,,,,)，

(1)

式中：、、、和分别为炸药的初始密度、屈服强度、剪切模量、定容比热和黏度；为椭圆孔洞的横截面积；为无量纲参数半轴比，=；为椭圆孔洞倾斜角；、、、分别为炸药初始的比内能、温度、粒子速度和压力。

首先，考虑到在强冲击载荷下孔洞坍塌过程具有高压特征，炸药的初始状态对热点形成的影响可以忽略不计,这意味着Δ可以被认为与初始压力、初始粒子速度、初始比内能和初始温度无关。此外，与冲击强度(在点火压力附近，通常在几个吉帕的数量级)相比，炸药的屈服强度通常要小得多。如本文研究使用的PBX，屈服强度=0044 85 GPa，冲击强度=36 GPa，因此=0012 1≪1在如此小的值下，孔洞坍塌通常表现为射流冲击坍塌，这说明屈服强度变化对于孔洞坍塌过程影响不大，当然对热点温度的变化几乎没有影响。 因此，(1)式可简化为

Δ=(,,,,,,,)

(2)

在质量、长度、时间、温度(MLTK)类单位制中，(2)式所涉及的每个量量纲分别为

dim Δ=, dim=MLT, dim=ML, dim=MLT, dim=LTK, dim=MLT, dim=L, dim=dim=1

(3)

显然，、、和的量纲是相互独立的，将这4个变量作为研究动态加载下非均质固体炸药内部椭圆孔洞坍塌问题的基本单位系统，用来度量问题中的所有物理量，则(3)式中剩余的变量可以分别表示为

dim Δ=dim (()), dim=dim, dim=dim ()12

(4)

因此，利用定理，可以将(2)式写成如下的无量纲形式：

=(,,,)，

(5)

式中：(·)表示任意函数；、、、和分别为

(6)

(6)式代入(5)式，可得

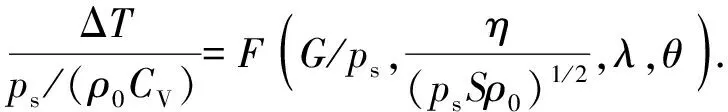
(7)

(7)式中现存的无量纲参数可以用不完全相似或第2类自相似进一步简化。

然后，对无量纲参数进行分析研究。一般来说，PBX的剪切模量与冲击强度(在点火压力附近)是一个数量级。例如，本研究中使用PBX的剪切模量，=38 GPa在冲击强度=36 GPa(点火压力附近)加载下，有= 106，介于110与10之间。根据文献[31]，参数被认为是基本的，问题对参数没有完全相似性。然而也存在例外，使得能够减少变量的个数，可以假设函数(·)具有任意幂律型渐近表达式，即问题对参数具有不完全相似性或者第2类相似性，则(5)式可以进一步简化为

(8)

式中：为待定常数；(·)表示关于、和的任意函数。

最后，考虑无量纲参数在=36 Gpa、=1257 μm、=1845 g/cm和=31 Pa·s的条件下，无量纲参数=037，介于110与10之间。与类似，根据文献[31]，问题对参数具有不完全相似性或者第2类相似性，则可以假定另一个函数(·)为幂律型渐近表达式，(8)式可以进一步写成以下更简单的形式：

(9)

式中：是另一个待定常数；(·)表示关于和的任意函数。最后，(6)式代入(9)式，得

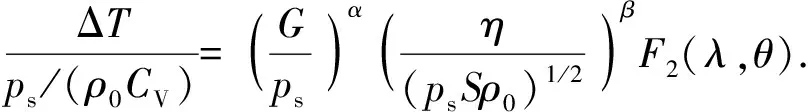
(10)

(9)式中待定常数、和函数(,)由数值实验结果确定。

2 数值模拟

2.1 守恒方程和本构关系

在欧拉坐标系中，控制方程由一组双曲守恒方程组成，分别包括质量守恒、动量守恒和能量守恒：

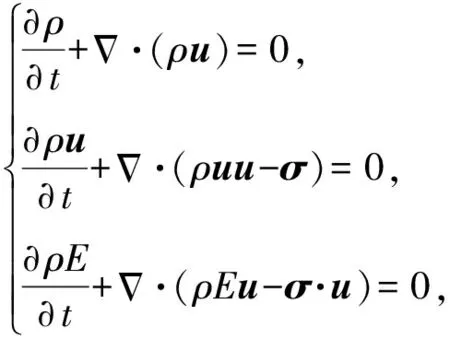
(11)

式中：为质点速度；为柯西应力张量；和分别为所考虑材料的密度和总比能(包括内能和动能)。

本文采用弹塑性流体动力本构模型来描述PBX的力学行为。为此，将柯西应力分解为偏应力和膨胀应力两部分，其分量形式可以写为

=-，

(12)

式中：为偏应力张量，是一个2阶张量；为所考虑材料的压力；为克罗内克函数。

Gruneisen状态方程被用来描述PBX的膨胀行为，如(13)式所示：

(13)

式中：和为描述-Hugoniot曲线的常数材料参数，和分别为冲击波波速和波后粒子速度；为Gruneisen系数。表1给出了PBX-1的材料属性值和模型参数。

表1 PBX-1的状态方程参数Tab.1 Equation of state parameters for PBX-1

材料本构行为的偏量部分分为弹性响应和塑性响应。弹性偏应力- 应变关系符合一般的胡克定律：

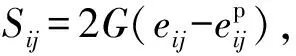
(14)

(15)

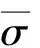
(16)

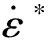
表2 PBX-1炸药的Johnson-Cook模型参数Tab.2 Parameters of Johnson-Cook model for PBX-1

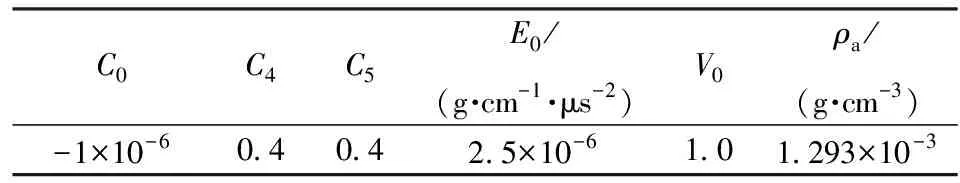
表3 空气的模型参数Tab.3 Model parameters for air

2.2 数值模型

本文采用有限元分析软件LS-DYNA对嵌入在均匀PBX炸药中的二维椭圆孔洞(见图1)进行数值模拟。计算域的大小为30 μm×30 μm，在计算域的左端施加一定幅值的阶跃冲击载荷，并且在边界上施加以下边界条件：在右边界上有非反射的边界条件，在上下边界上有对称条件，PBX最初是静态、无应力的。在建模过程中，采用欧拉方法和2阶精度平流算法Van-Leer，使用时间间隔0.2 ns对历史数据进行采样。

网格分辨率被认为在多孔含能材料的中尺度模拟中起着一定的作用。因此，为了验证该方法的有效性和准确性，首先对一个含有圆形孔洞的PBX-1炸药典型案例进行数值模拟，其中孔洞半径为3 μm，PBX-1炸药尺寸为30 μm×30 μm，冲击强度为3.6 GPa. 在模拟中分别考虑100×100、200×200、300×300和 400×400 4种网格尺寸，4种网格尺寸下孔洞坍塌导致的最大质点速度和最高温度随时间变化的数值模拟结果如图2所示。由图2可以看出，随着网格数量的增加，最大质点速度和热点最大温度都有所增加，300×300网格计算的数值结果与400×400网格计算的数值结果吻合较好，表明数值结果收敛。也就是说，当网格数大于300×300时，可以得到网格无关解，这也与文献[15,18]的结果一致。为了保证较高的精度和节省计算量，所有的数值模拟都采用300×300网格进行。

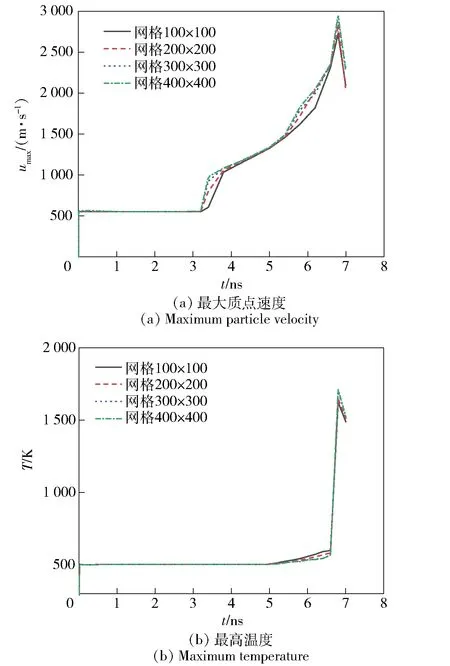
图2 初始冲击强度3.6 GPa、孔洞半径3 μm时的 数值模拟结果Fig.2 Numerical results under the initial shock loading of 3.6 GPa with the initial void radius of 3 μm

2.3 数值模拟结果和分析

为研究椭圆孔洞的伸长状态(即半轴比)对热点温度的影响，对=78.54 μm不同伸长状态下(=4, 3, 2, 1;=0°)的椭圆孔洞进行数值模拟，其中冲击强度为3.6 GPa. 此外，为研究椭圆形孔洞位置对热点温度的影响，在相同的冲击强度下，将位于不同位置(=2;=0°, 30°, 60°, 90°)的椭圆型孔洞(=78.54 μm)的坍塌过程进行模拟。为了直观地看出不同伸长状态下和不同孔洞位置对孔洞坍塌过程的影响，表4给出了一部分不同伸长状态和位置的孔洞坍塌过程。

由表4可以看出，由于孔洞位置和伸长状态的不同，孔洞坍塌经历的阶段有所不同。倾斜角较大的椭圆孔洞坍塌仅仅经历了塑性变形，在坍塌过程中不会形成射流。倾斜角较小的椭圆孔洞坍塌会经历以下3个阶段：1)激波到达孔洞上表面时孔洞发生局部塑性变形；2)孔洞上表面的大部分颗粒向中心线和下表面收敛，形成射流；3)射流与孔洞下表面发生碰撞。图3和图4分别给出了椭圆孔洞在不同伸长状态和不同位置下的最大质点速度和热点温度的数值模拟结果。由图3和图4可得，在=0°下，伸长状态较大的孔洞会形成较高的粒子速度，然后由于粒子的汇聚而产生较高质量和高速度射流，冲击下表面从而导致较高的热点温度。实际上，一方面，随着孔洞伸长状态的增加和孔洞摆放位置的减小，孔洞上表面卸载区域和形成的反射稀疏波逐渐减小，使得热点温度的增加幅度越来越大；另一方面，随着孔洞伸长状态的增加和孔洞摆放位置的减小，粒子加速运动的时间变长，在下表面发生碰撞的射流速度更高，使得热点温度升高。此外，为了获得热点温度对椭圆孔洞的伸长状态和摆放位置的依赖关系，对更多的孔洞伸长状态和孔洞摆放位置进行数值模拟，热点温度对各种伸长状态和摆放位置的数值结果如表5所示。由表5还可以看出：当椭圆孔洞的伸长状态=4和摆放位置=0°时,热点温度最高为2 990 K;当椭圆孔洞的伸长状态=4和摆放位置=90°时，热点温度最低为1 278 K对于位于不同伸长状态和摆放位置的孔洞，其最大热点温度比最小值大134左右，这明显说明孔洞形状和摆放位置对热点温度的影响是非常大的。

表4 4种状态下椭圆孔洞塌缩的演化过程

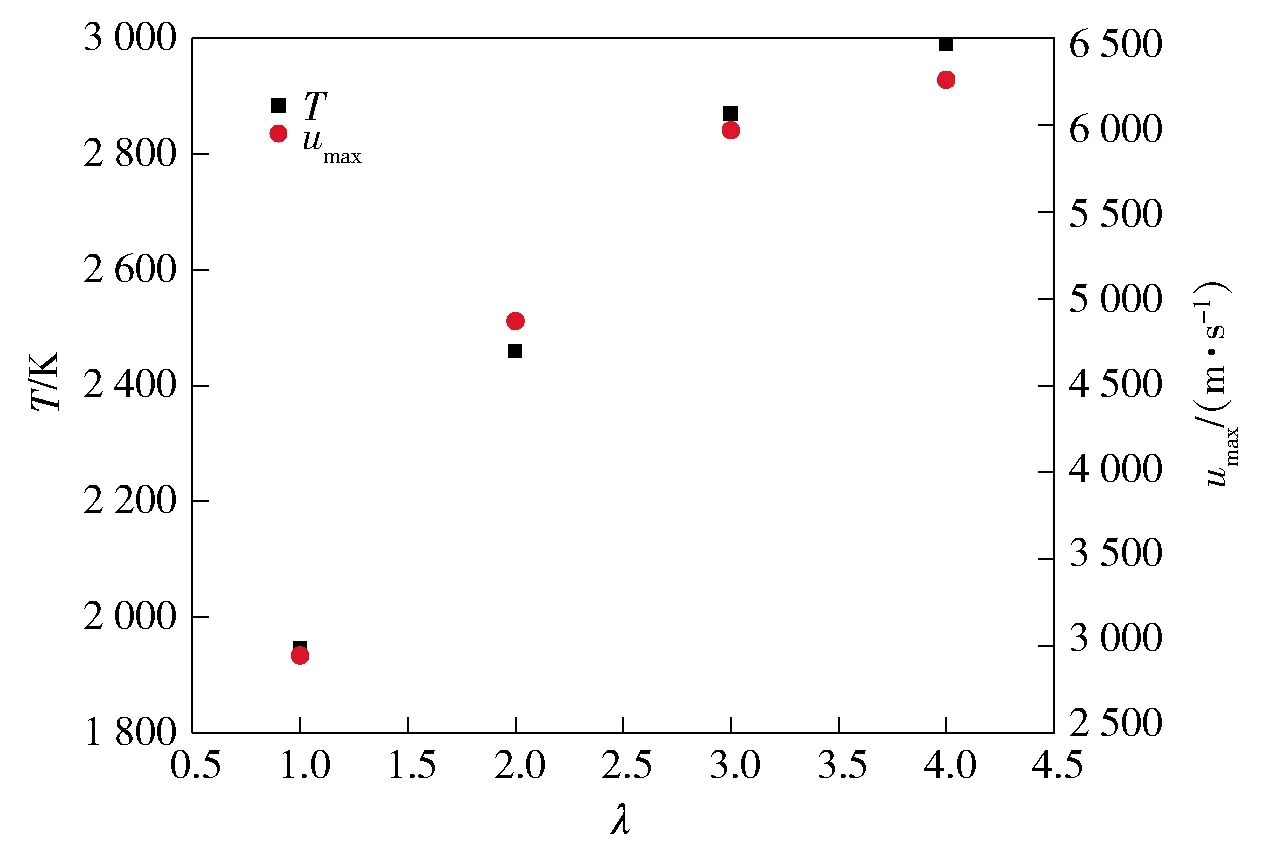
图3 热点温度和最大质点速度与孔洞伸长状态的 关系(θ=0°)Fig.3 Relations between hot-spot temperature and maximum particle velocity with void elongated state (θ=0°)

图4 热点温度和最大质点速度与孔洞位置的关系(λ=2)Fig.4 Relations between hot-spot temperature and maximum particle velocity with void positions (λ=2)

由以上分析可以看出，热点温度与嵌入PBX的椭圆孔洞伸长状态和位置有显著的关系，这说明椭圆孔洞的伸长状态和摆放位置对炸药的冲击灵敏度有较大的影响。多年来，在建立炸药起爆的大中尺度模型时，通常采用圆形孔洞假设来描述中尺度缺陷，这种假设可能造成炸药中热点温度与真实情况存在差异，导致对PBX起爆的预测存在一定的偏差。不同孔洞位置和伸长状态下的孔洞坍塌研究表明，仅用孔洞体积来表征炸药的冲击灵敏度似乎不太合理。

为研究孔洞尺寸对热点温度的影响，对伸长状态=2和摆放位置=0°的椭圆孔洞在不同截面面积(6.28 μm,14.13 μm,25.12 μm,39.25 μm,56.52 μm和76.93 μm)下进行了数值模拟。在所有的数值模拟中，冲击强度仍然为3.6 GPa. 不同孔洞尺寸PBX的热点温度数值结果如图5所示。由 图5可知，随着孔洞尺寸的增大，热点温度逐渐升高。造成这种现象的一个可能原因是，较大孔洞有足够的时间加速粒子运动，从而形成较高速度的射流，并且在下表面发生碰撞，获得较高的热点温度。

表5 不同孔洞位置和伸长状态下的热点温度Tab.5 Hot-spot temperatures at the various positions and elongated state of void

图5 热点温度与孔洞截面面积的关系Fig.5 Relation between hot-spot temperature and void cross-sectional area

最后，本文研究了冲击强度(冲击强度范围1～10 GPa)对热点温度的影响。其中，椭圆孔洞的横截面面积=78.54 μm和孔洞伸长状态=2(对应于半径=7 μm,=3.5 μm)。一些典型的孔洞坍塌过程如表6所示。由表6可以看出，当激波到达孔洞上表面时，孔洞上表面受到激波作用开始发生塑性变形。对于较低的冲击强度(如=1 GPa)，不能形成射流，说明在很弱的冲击作用下，孔洞的坍塌是由塑性变形控制的。然而，对于较高的冲击强度(如=5 GPa)，可以形成典型的射流，然后撞击孔洞下表面。热点温度的数值模拟结果如图6所示。由图6可以看出，随着冲击强度的增加，热点温度明显升高。事实上，更强的冲击总是意味着更高的动能或热能的输入。

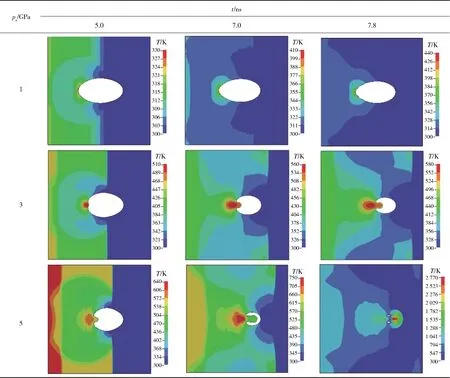
表6 不同冲击强度下孔洞坍塌演化过程

图6 热点温度与冲击强度的关系Fig.6 Relation between hot-spot temperature and shock intensity

3 热点温度的半经验解析表达

如第1节所述，通过相似分析，可以得到HMX基PBX热点温度的解析表达，如(10)式所示。为进一步确定(10)式中任意函数(,)以及模型常数、，不同因素(椭圆孔洞伸长程度、孔洞摆放位置、孔洞面积、冲击强度)对热点温度影响的数值结果被使用。为此，给出不同条件下的热点温升Δ(见图7)，然后利用Levenberg-Marquardt优化算法对这些数值模拟结果进行数值拟合。

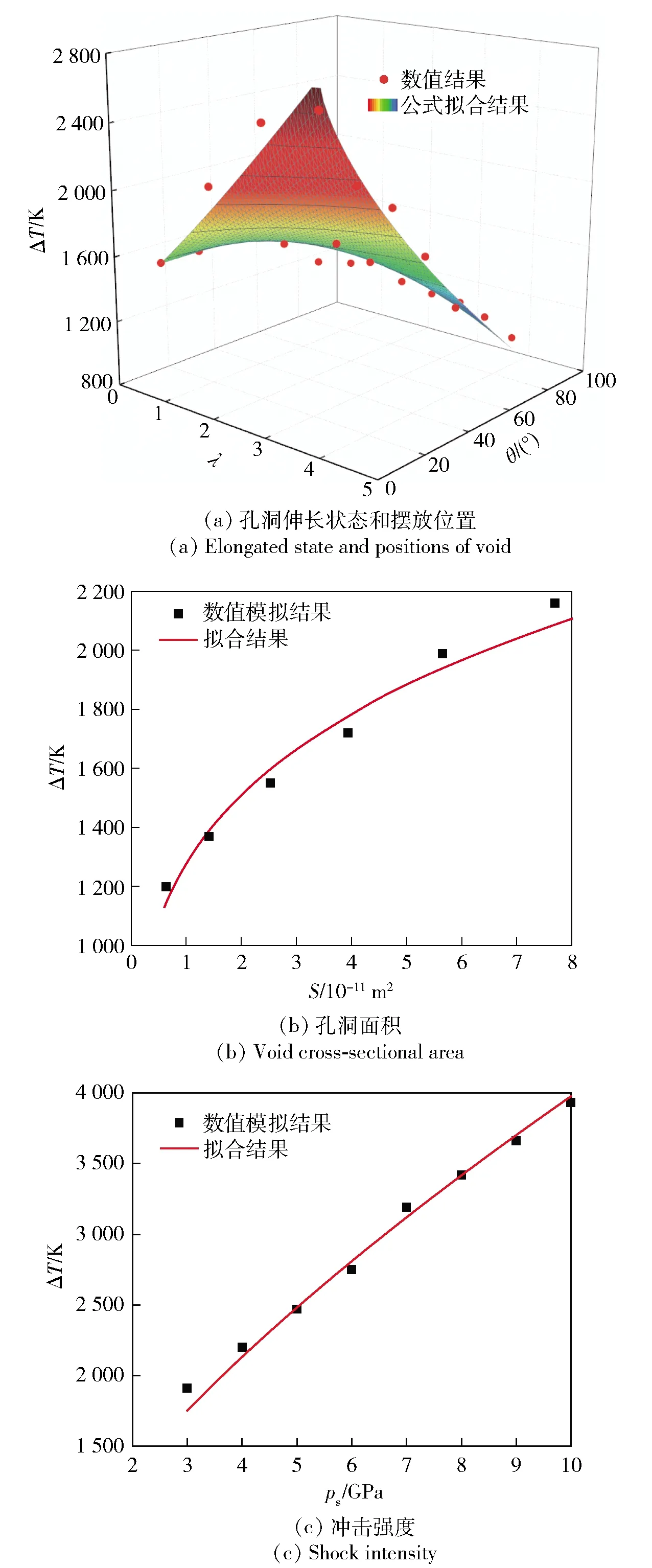
图7 热点温升与各因素的关系Fig.7 Relation between hot-spot temperature rise and various factors

为确定任意函数(,)，对上述数值结果进行分析。由图3可以看出，倾斜角为常数时，热点温升对孔洞伸长状态的依赖关系可以近似地用幂函数的形式表达，也就是，Δ=+,其中、和是常数。相似的，当椭圆孔洞的伸长状态是常数时，热点温升对倾斜角的依赖关系也可以用幂函数的形式表示，即Δ=+，其中、和为常数。对于圆形孔洞(=1)，热点温度的升高并不随孔洞位置的变化而变化，这表明新的实验函数为Δ=+(-1)因此，当其他参数(冲击强度和椭圆孔洞面积)固定时，考虑两个变量和的耦合作用，一个新的函数被得到，可以写成如(17)式形式：

Δ=(,)=Δ+Δ=+++(-1)，

(17)

式中：为常数。因此，(,)可以写成以下更简单的形式：

(,)=++(-1)，

(18)

式中：、、、、为(,)的5个待定常数参数。

(18)式代入(10)式，可得

(19)

(19)式中的参数可以通过一些数值实验结果来确定。以PBX-1炸药为例，函数Δ的拟合结果如图7所示，通过数值拟合得到的所有模型参数如表7所示。

综上所述，对于PBX-1炸药，得到热点温升的半经验解析表达式为

(20)

或者写成热点温度(室温=300 K)，有

0.014(λ-1)θ0.70). (21) 表7 参数α、β以及函数F2(λ,θ)的系数Tab.7 Parameters α, β and the coefficient of functionF2(λ,θ)

最后，为验证半经验解析表达式的可靠性，进一步对其他不同情况进行了更多的数值模拟以及使用半经验解析表达式求解，并对数值结果和理论预测结果进行对比，如图8所示。从图8中可以看到,热点温度的理论预测结果与数值模拟结果相一致，并且理论预测结果与数值模拟结果的相对误差基本上不到10，如表8所示。这意味着半经验解析表达式可以用来描述热点温度与椭圆孔洞尺寸、伸长状态和摆放位置以及冲击强度的依赖关系，它为建设细观热点点火反应速率模型提供了一个良好的基础。

图8 不同条件下数值模拟结果与理论预测结果对比Fig.8 Comparison of numerical results and theoretically predicted results under different conditions

此外，热点区域可以近似看成是一个体积近似 为原孔洞体积，温度由中心向四周逐渐递减的球形区域，如表4所示。从表4中可以看出，热点中心区域温度为热点最大温度，热点最外围区域的温度可以近似为冲击后炸药的整体温度(即非热点区域温度)，则一个半径为的热点区域温度分布为

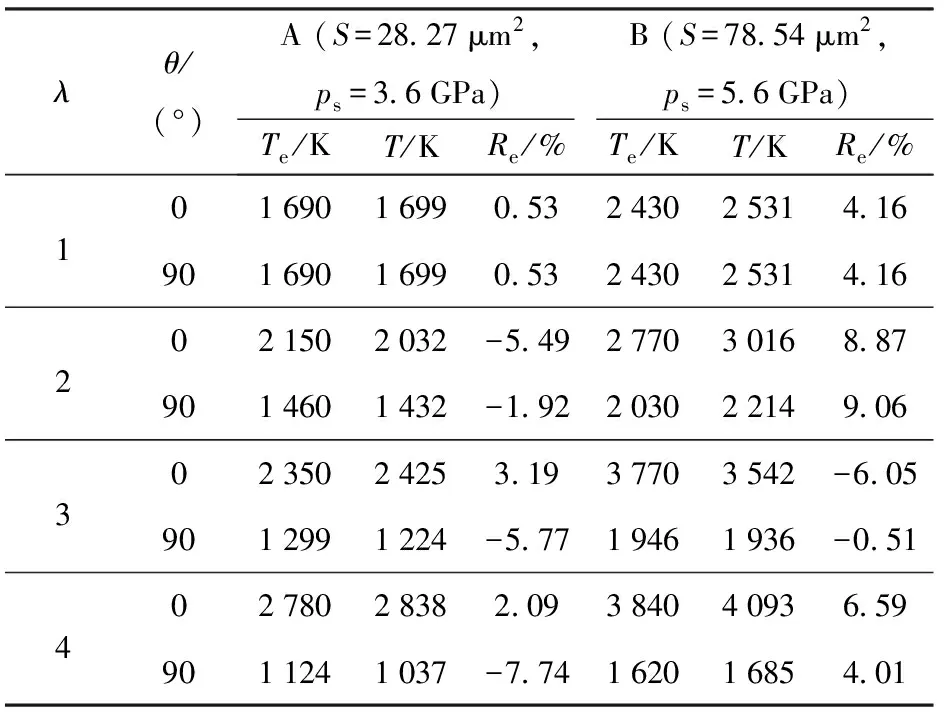
表8 (21)式预测结果和数值模拟结果的 相对误差ReTab.8 Relative-error Re between predicted results of Eq.(21) and numerical results

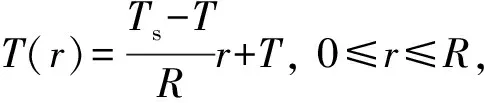
(22)

式中：为热点区域任意点到中心位置的距离。

通过对热点区域的能量积分求得热点区域的总能量，然后通过能量均分定理得到热点区域的平均温度：

(23)

(22)式代入(23)式，得

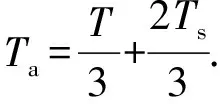
(24)

数值计算得到的不同冲击强度下非热点区域温度如图9所示。由图9可知，冲击强度和非热点区域温度之间为线性相关。通过线性拟合得到冲击强度与非热点区域温度之间的线性关系式为

=189+728×10

(25)

(21)式和(25)式代入到(24)式中，可得

=226+485×10+

(26)

图9 非热点区域温度与冲击强度的关系Fig.9 Relation between non-hot spot region temperature and shock intensity

4 结论

本文通过相似性分析和中尺度数值模拟，全面研究动态加载下PBX中椭圆形孔洞坍塌对热点温度的影响，主要涉及孔洞尺寸、伸长状态和位置以及冲击强度。 得出主要结论如下：

1)除了椭圆孔洞的尺寸、伸长状态和冲击强度外，孔洞的摆放位置对热点温度也有较大的影响，即热点温度随倾斜角的增大而降低。在3.6 GPa的冲击压力下，当椭圆孔洞(面积=78.54 μm)的伸长状态=4和摆放位置=0°时，热点温度最高为=2 990 K，比同面积下圆孔洞产生的热点温度(1 946 K)高54%左右，这意味着通常的圆形孔洞假设会导致对PBX起爆的预测存在一定的偏差。因此，在构建中尺度热点模型时，仅用孔洞体积来表征孔洞对炸药冲击敏感性的贡献是不合理的，必须考虑孔洞的构型。

2)基于中间渐近，完全相似和不完全相似的相似性理论，得到PBX热点温度的半经验解析表达式，可以很好地预测热点温度关于椭圆形孔洞几何尺寸、摆放位置以及冲击强度的依赖性。具体地，对于HMX基PBX，发现由半经验解析表达式获得的热点温度的理论结果与数值模拟结果吻合良好。

3)基于得到的热点最大温度，通过对热点区域的能量积分求得热点区域的总能量，然后通过能量均分定理得到热点区域的平均温度。