铁路接触网作业车运行优化研究
2022-03-12钟永红
钟永红
(中国铁路武汉局集团有限公司宜昌综合维修段,湖北 宜昌 443100)
随着高铁技术的快速发展和铁路里程的不断增加,我国成了名副其实的轨道交通强国。在整个铁路运行系统中,接触网作业车具有十分重要的地位[1]。一方面,接触网作业车可以配合运载车辆的电能获取;另一方面,接触网作业车肩负着整个轨道系统的架线、立杆等维修任务[2]。尤其是接触网作业车承担了大量的轨道系统夜间巡视和维修任务,可以在很大程度上节省人力[3]。在这种情况下,接触网作业车如何安全可靠地运行成为轨道交通系统稳定运营的重要问题。这就需要对接触网作业车的工作状态进行准确分析,尤其是进行运行过程中的力学分析,进而根据高性能的控制算法对接触网作业车的运行轨迹进行优化和合理控制,全面提升接触网作业车的运行效率和自主驾驶性能。该文在单质点模型下从牵引力、制动力、运行阻力等方面对接触网作业车的运行过程进行受力分析,进而根据遗传算法优化接触网作业车的运行路线,以期获得更好的安全性、舒适性和运行效果。
1 铁路接触网作业车运行过程中的受力分析
根据不同的作业需求,铁路接触网作业车有不同的类型,大致可以分为7 种:第一种,架线车,负责轨道系统的架线操作;第二种,检修车,负责对整个轨道系统进行检修;第三种,起重车,负责轨道系统内的重物装卸和搬运;第四种,立杆车,负责在轨道系统内假设标杆;第五种,冲洗车,负责对轨道系统和关键部件进行冲洗作业;第六种,放线车,负责在轨道系统内进行放线作业;第七种,钻专用板车,负责在轨道系统内的钻孔作业。
该文以JW-4G 型号的检修车为例,对其进行运行优化方面的研究。JW-4G 型检修车包括液压单元、升降单元、动力单元、制动单元、起重单元、行驶单元、检测单元和电气单元。该文的研究涉及行驶单元、动力单元、制动单元,主要是针对行驶单元。
在对接触网作业车进行受力分析的过程中,一般要将接触网作业车进行简化处理,常见的做法是用单质点模型或多质点模型加以代替。多质点模型更复杂,并且需要考虑各质点之间的力学关系,不易求解。因此该文用单质点模型代替JW-4G 型检修车本体进行受力分析。
接触网作业车在运行过程中会受到多种外力的影响。除了重力、支持力等垂直方向的力以外,还要受到牵引力、接触面的摩擦力等水平方向上的力。据此,该文给出JW-4G 型检修车单质点模型下的受力分析,如图1 所示。

图1 JW-4G 型检修车单质点模型下的受力分析
如图1 所示,JW-4G 型检修车所受到的合力的计算如公式(1)所示。
式中:C为检修车运行过程中所受到的合力;F为检修车运行过程中所受到的牵引力;B为检修车运行过程中所受到的制动力;WC为检修车运行过程中所受到的附加阻力;W0为检修车运行过程中所受到的基本阻力。
根据经验,JW-4G 型检修车所受到的最大制动力的计算如公式(2)所示。
式中:Bmax为检修车运行过程中的最大制动力;B为检修车运行过程中的当前制动力;v为检修车的运行速度;φ为检修车的制动角度。
从公式(3)中可以看出,如果在低速状态下运行,检修车以恒定的制动力加以控制。如果超过了73 m/s 这个速度临界值,检修车的最大制动力就需要根据二元一次方程进行计算。
2 铁路接触网作业车运行遗传算法优化
JW-4G 型检修车在作业过程中,由于人的参与和作业任务的需求,需要同时保证检修车运行的平稳性、舒适性,还需要确保检修车能够及时达到工作点位和准确停车。因此,对JW-4G型检修车运行控制的关键在于对车体速度的控制。为了达到良好的控制效果,改文采用遗传算法对JW-4G型检修车车体速度进行控制。
遗传算法是根据基因遗传规则设计出的一种优化方法,它从初始种群开始,在满足各种规则约束的前提下运用遗传过程中的操作,不断更新适应度函数直到适应度函数满足迭代终止的条件。对应于该文的问题,运行的平稳性、舒适性、工作点位的及时到达和准确停车就是该文遗传算法执行的约束条件。遗传算法采用的主要操作包括选择、交叉和变异,下面将分别加以阐述。
2.1 遗传算法的选择计算规则
根据基因遗传的一般规律,父一代向子一代遗传,总是尽可能选择更好的基因,而父一代的劣质基因会尽可能地被摈弃。对遗传算法而言,基因的好与坏是通过适应度函数的函数值高低来判断的。从数学角度看,高适应度的函数值是以概率的形式反应给选择操作的,具体处理如公式(4)所示。
式中:Fit(k)为遗传算法设定的适应度函数对应于第k 种概率的值;p(k)为遗传算法根据适应度函数可能选择第k种变化的概率。
按照这个公式,更高概率的变化将作为遗传给子一代的选择结果。
2.2 遗传算法的交叉计算规则
遗传算法通过多个父代基因的重组可以增加子一代基因的丰富性。交叉计算就是2 个父一代基因的交叉,进而可以得到子一代中含有2 个或2 个以上父一代基因的染色体的过程,交叉计算的说明性实例如图2 所示。
从图2 中给出的遗传算法的交叉计算说明性实例,可以看出2 个父代染色体之间的交叉计算满足如下的规则。
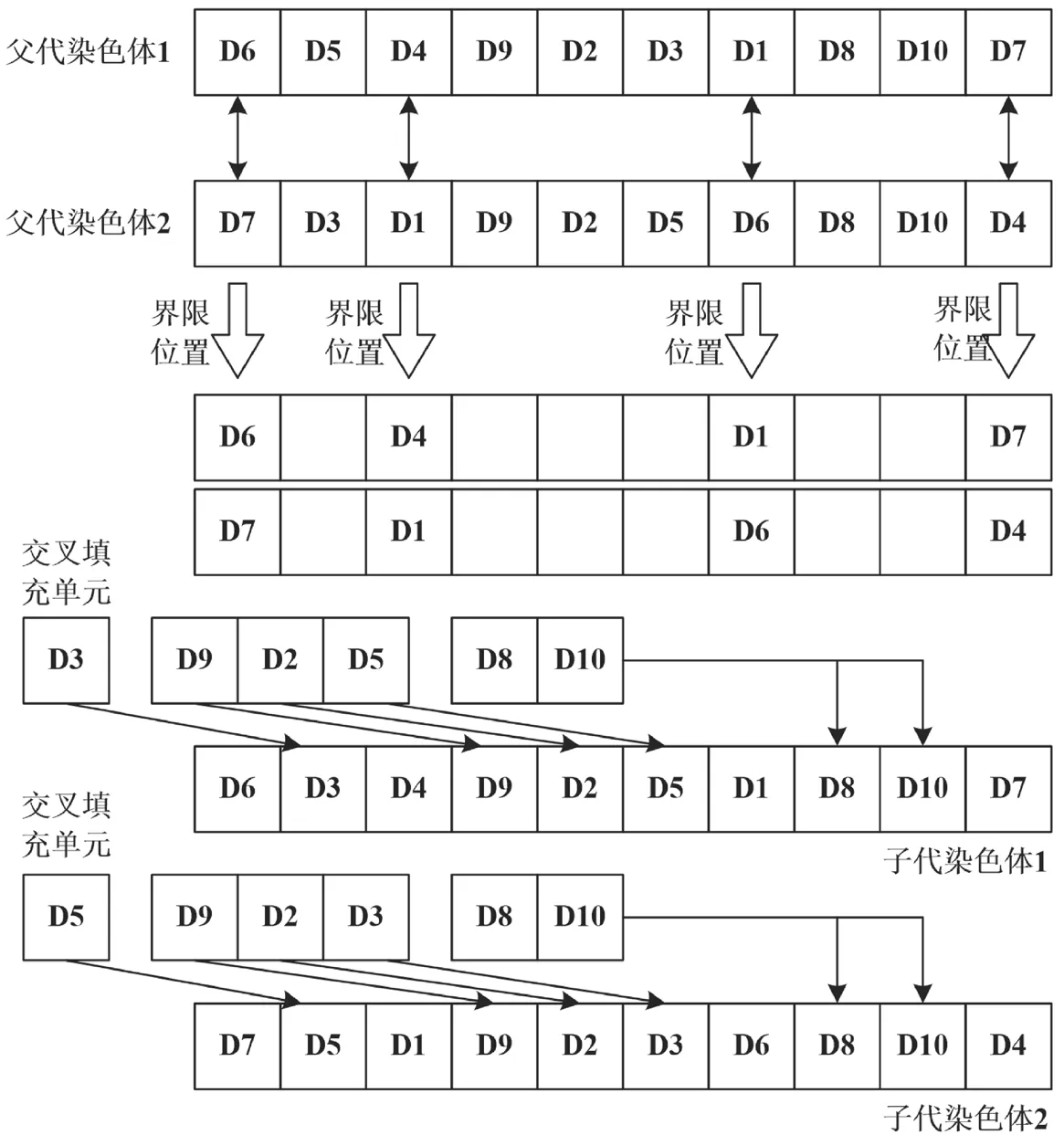
图2 图遗传算法交叉计算的说明性实例
规则一:2 个父一代基因组向子一代传递,但这2 个基因组中相同的基因只保留一个,不重复向子一代传递。
规则二:2 个父一代基因组中,如果存在特别优良的基因,即适应度函数值特别高的基因,无条件向子一代传递。
规则三:按照上述2 个规则执行以后,子一代染色体中会留下一些空缺的位置,由父一代染色体中的基因按位置对应关系填充,完成子一代染色体的生成。
2.3 遗传算法的变异计算规则
如果完全按照适应度函数值的高低、参与交叉计算的父一代染色体向子一代遗传,那么子一代不会出现明显的进化。根据实际遗传的规律,子一代染色体会因变异而获得父一代没有的基因。为此,遗传算法也对应设计了变异计算的规则,变异计算的说明性实例如图3 所示。
从图3 给出的遗传算法变异计算的说明性实例可以看出,父一代染色体的个别位置上的基因出现了突变的情况,形成了变异遗传的效果。
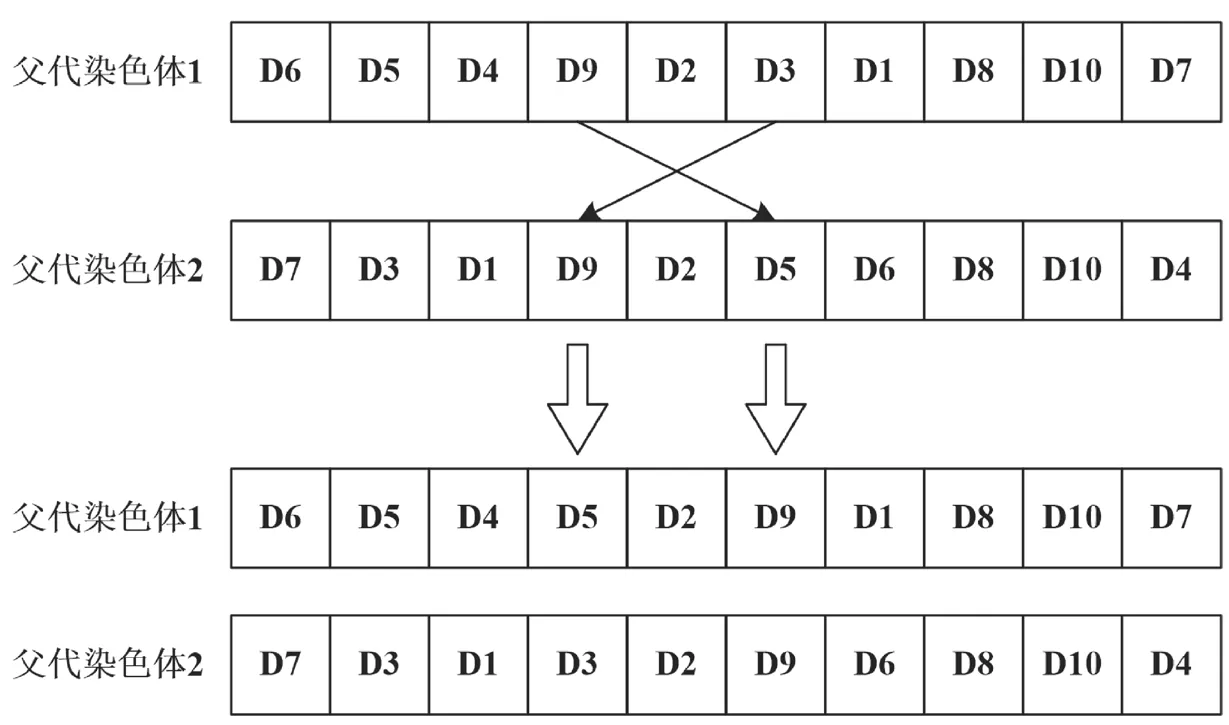
图3 遗传算法变异计算的说明性实例
3 铁路接触网作业车运行优化试验与分析
为了验证遗传算法对JW-4G 型检修车运行优化的效果,接下来进行试验研究。试验过程中,选择的JW-4G 型检修车整体质量达到了47 t,运行过程中遇到的阻力是2.4 kN。整个车体系统的传动效率大于93%,因阻力损耗的占比不足7%。负责检修车牵引的发动机的额定功率为360 kW。承载检修车的车轮半径为0.5 m,控制检修车动作的轴数为4 个,轴间距为2.4 m。检修车运行过程中,最高时速不得超过120 km/h,最小制动距离不得超过400 m,否则会带来安全隐患。在这个最小制动距离的约束下,制动速度不低于80 km/h。
对遗传算法的设定:第一个约束条件设定了检修车运行总里程为20 000 m,第二个约束条件设定了检修车运行总时长为1 240 s,遗传算法的初始种群基因个数为400,遗传代数即最大迭代次数为100 次,遗传算法选择计算的概率判别值为0.5,遗传算法交叉计算的概率判别值为0.5,遗传算法变异计算的概率判别值为0.1。
根据上述设定,采用遗传算法对JW-4G 型检修车进行运行速度优化控制,得到的速度变化曲线如图4 所示。
从图4 可以看出,在遗传算法的控制之下,JW-4G 型检修车的运行速度曲线光滑,代表着行车过程平稳、车载人员的舒适度很高。同时,JW-4G 型检修车的运行速度始终控制在区段限速的速度值之下,也低于接触网作业车标准限速(GYK)速度值的规定,安全性稳定可靠。
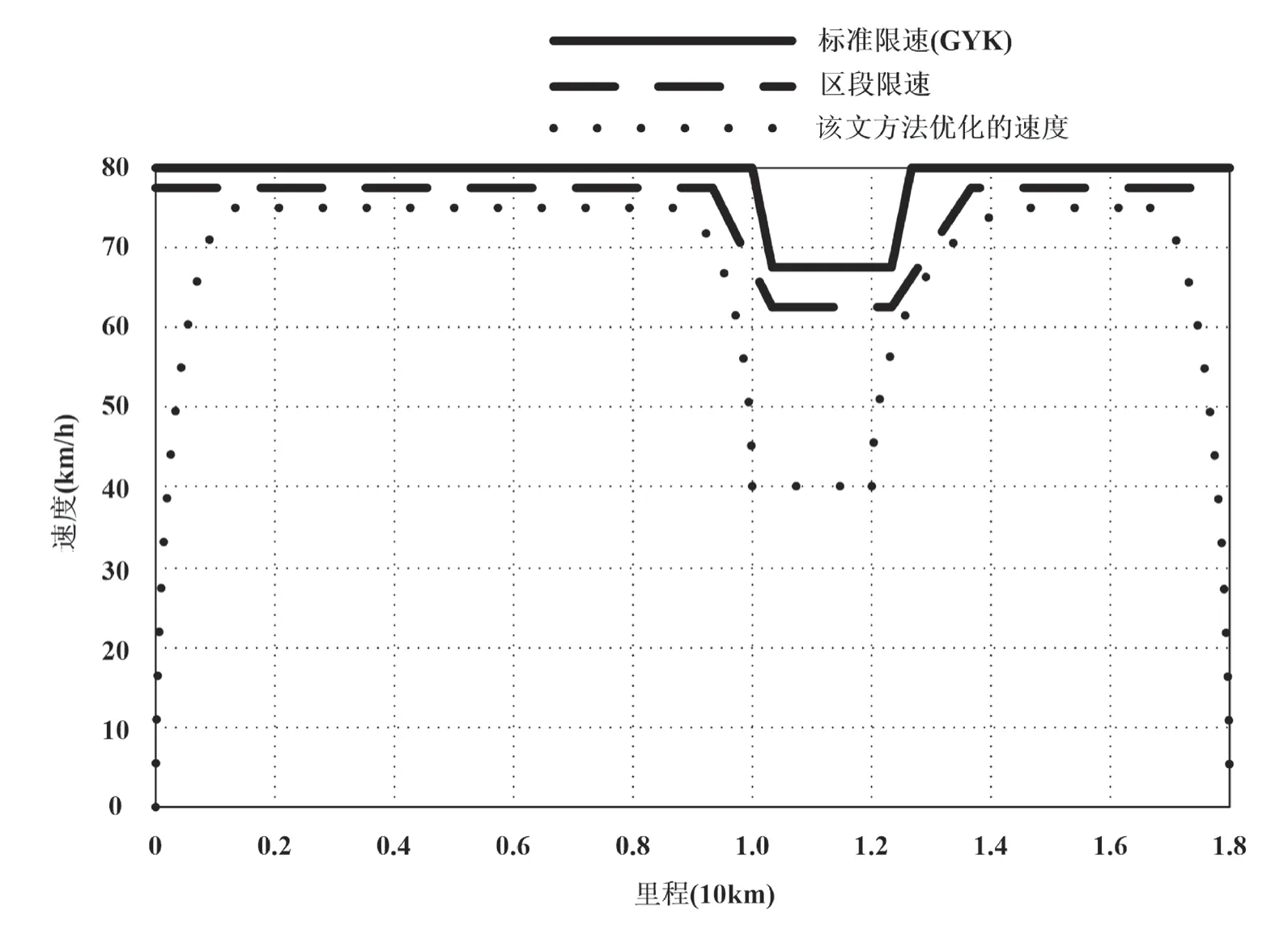
图4 遗传算法对JW-4G 型检修车进行运行速度优化的控制曲线
进一步选择其他4 组JW-4G 型检修车在常规控制下动作,作为该文算法控制动作的参照,对比结果见表1。
从表1 给出的对比结果可以看出,采用遗传算法进行运行优化控制后,JW-4G 型检修车在准时度、精准度、舒适度、节能度4 个方面均有明显提升,取得了更好的运行控制效果,证明了该文提出方法的有效性。
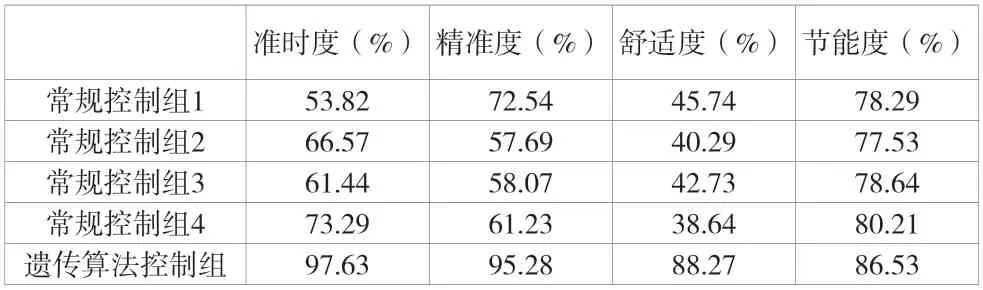
表1 5 组JW-4G 型检修车运行控制性能的对比
4 结论
随着我国逐步成为轨道运输大国和强国,铁路接触网作业车的重要程度也日益凸现。为了进一步提升接触网作业车的运行效果,该文在遗传算法的基础上提出了一种运行优化控制算法。首先确定了JW-4G 型检修车作为接触网作业车的具体案例,成为常见的7 类接触网作业车的代表。其次,对JW-4G 型检修车运行过程中的状态进行了受力分析。再次,以速度优化为运行优化控制的核心目标,构建了遗传算法的优化控制策略,给出了遗传算法的约束条件、交叉计算规则、选择计算规则、变异计算规则。试验结果表明:在遗传算法的控制下,JW-4G 型检修车运行过程平稳、安全度高,与常规控制下的运行状态相比,在准时度、精准度、舒适度、节能度4 个方面均有明显提升。
