基于SPH-FEM方法的直升机典型金属结构入水冲击分析

简成文 吴远飞

（中国直升机设计研究所，江西 景德镇 333001）

0 引言

飞机在高空高速飞行，当遇到紧急情况时必须迫降。飞机的迫降形式主要有3 种：场内迫降、场外迫降和水面迫降。其中，水面迫降是指着陆场在海洋、湖泊以及河流等水面上，水面迫降要求尽可能地靠近陆地，主要采用3 种方法（试验法、解析法以及数值仿真法）对飞机水上迫降性能进行研究。20 世纪80 年代以前，研究人员主要通过动力相似缩比模型试验来研究飞机的水上迫降性能。然而，随着计算机科学技术的发展，飞机的全机模拟仿真以其精度高、成本低以及效率高的优点逐渐取代了试验的研究方法。Anghileri M 等[1]对近似刚体结构进行入水试验，并用SPH 方法进行仿真，对无量纲的加速度和压力结果进行对比，数据吻合度较高。金属板结构是直升机结构中最常见的结构，对直升机典型金属板结构入水冲击响应进行研究，可以为后续直升机整机入水仿真分析奠定基础。该文采用SPH-FEM 流固耦合计算方法对金属板结构入水冲击响应进行研究。

1 SPH-FEM 流固耦合计算方法

SPH粒子与有限单元通过定义接触的方式进行流固耦合计算。将有限单元的节点视为背景粒子，背景粒子的变量与相应的有限单元节点一致，例如粒子质量、位置、速度和应力等[2-3]。背景粒子只能被其他SPH 粒子搜索，在每个时间步内，接触部分的相关信息会从背景粒子传递到有限元数据中。对有限元部分来说，这种传递相当于施加边界条件，对SPH 部分来说，有限单元节点转化为邻近粒子，从而避免了边界影响，进而使SPH 粒子与有限元之间具有很好的连续性。

位于有限元节点支持域内的SPH 粒子会对该节点产生接触力，同时位于SPH 粒子支持域内的有限元节点会对该粒子产生接触力，接触势能如公式（1）所示。式中：NCONT为粒子i的邻近粒子数；m为粒子质量；ρ为密度；K为接触罚刚度；rij为粒子间距；W为光滑函数（当xA、xB属于相同个体时，W（xA-xB）=0）；∆pavg为粒子间光滑长度的平均值；n为粒子总数；x为粒子位置。

接触力如公式（2）所示。

式中：∆为拉普拉斯算子。

对SPH 粒子来说，是将接触力施加到动量方程的，如公式（3）所示。

式中：ν为粒子的速度矢量；t为时间；N为粒子数量；σ为应力；∏ij为人工黏度项；x为密度、速度和能量等变量；α、β为常数，取值分别为0.04 和0.01；xi是粒子i的位置。

在SPH 方法中，Monoghan 型的人工黏性将动能转换为热能，同时防止粒子相互接近时出现非物理穿透现象，如公式（4）所示。

式中：c为声速；ϕ为粒子的形函数。

对大多数流体仿真来说，常数α∏和β∏的取值分别为0.04 和0.01。

对有限单元来说，接触力被当作外力施加到动力学方程，如公式（5）所示。

式中：、和u分别为加速度、速度和位移；M、C和K分别为系统的质量矩阵、阻尼矩阵和刚度矩阵。

SPH-FEM 流固耦合计算步骤如图1 所示。

图1 SPH-FEM 流固耦合方法计算示意图

2 金属板入水冲击动力学建模

2.1 SPH 水体模型

水体单元模拟采用Langrange实体单元和SPH粒子单元，当采用实体单元时，将实体单元赋予水动力（Hydrodynamic）材料，状态方程采用多项式状态方程，如公式（6）、公式（7）所示。

式中：Ci为材料常数；μ为无量纲参数；Ei为内能；ρ0为水体的初始密度；ρ为当前水体的密度。

当水体采用SPH 粒子单元时，将SPH 粒子单元赋予Monaghan 状态方程材料，状态方程如公式（8）所示。

式中：p0为水体的初始压强；ρ0为水体的初始密度；γ为常量，一般来说γ=7；B为状态方程中的系数。

当流体最大流速为vmax时，状态方程中的系数B如公式（9）所示。

考虑试验水池足够大，不考虑水池大小对仿真分析结果的影响，建立1 200 mm×1 200 mm×405 mm 的水域，水域由SPH粒子和实体单元耦合而成。其中，试验件与水体接触部分采用SPH 粒子模拟，该部分水域尺寸为800 mm×800 mm×100 mm，其余水域采用实体单元模拟。SPH粒子单元采用立方体形式，粒子间距为15 mm。

2.2 流固耦合接触模型

SPH 粒子与FEM 单元之间的流固耦合通过接触来设置。接触是边界条件高度非线性的复杂问题，需要追踪接触前物体的运动以及接触后物体之间的相互作用。在接触过程中，载荷随时间、结构的变形而变化，即结构与载荷互相耦合。

接触计算采用罚函数法，在每个时间步先检查从节点是否穿透主面，如果无穿透，就不做处理；如果穿透，就在该从节点与被穿透主面之间引入一个接触力，其大小与穿透深度、主面刚度成正比，从节点i受到的接触力Fi如公式（10）所示。

式中：SLFACM为接触刚度缩放因子；STF（SNODE）为主/从节点的接触刚度；gi为穿透厚度。

同时，非线性惩罚方式能够增加罚刚度，从而避免完全穿透。非线性罚刚度如公式（11）所示。

式中：ki为线性刚度；FSVNL为非线性刚度参数；Hcont为接触厚度；为非线性罚刚度。

其接触力如公式（12）所示。

该文对结构与水体之间的接触进行设置，定义SPH 粒子为从节点，结构为主面，建立相应的接触模型。

2.3 金属材料模型

在大变形状态下，金属材料结构的薄弱区域将出现应力集中的现象，当应力过大并超过材料弹性极限时，薄弱区域的材料将进入塑性状态，线弹性的本构关系不再适用，需要满足相应的屈服准则。而屈服准则是在外部载荷作用下，物体内某一点开始产生塑性变形时应力所必须满足的条件。

金属材料属于各向同性材料，该文中金属的强度准则采用最大线应变准则，定义如下：当材料最大线应变ε1（或|ε3|）达到极限值时，材料发生破坏。其表达式如公式（13）所示。

式中：εT、εC分别为材料拉伸、压缩时的极限应变。

在仿真计算中，当壳单元应变达到预期最大应变值时单元失效并删除单元。

2.4 结构有限元模型

对元组件进行简化，抽取相应的框架及面板中面，对结构焊接部分进行共节点处理，对底部试验件的螺栓连接建立相应的弹簧元。为了模拟在吊篮顶部施加质量块，建立相应的刚体约束，并在刚体中心点施加质量点。试验件及组件采用四边形壳单元模拟，单元尺寸为10 mm×10 mm。

试验装置结构如图2 所示，有限元模型如图3 所示。

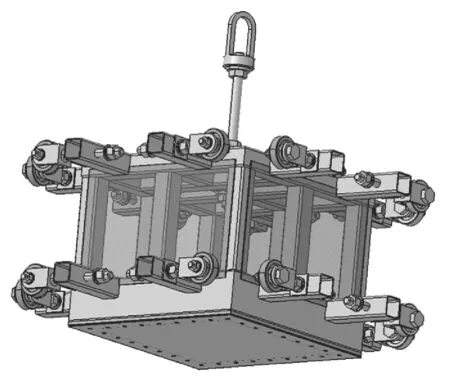
图2 试验装置结构图

图3 有限元模型

3 金属板入水冲击试验

3.1 试验条件

试验装置由水池、试验件、吊篮、导轨、台架以及释放装置组成。试验件安装在吊篮底部，试验件上布置应变片。吊绳与吊篮相连，通过起吊装置及其控制系统调整吊篮的起吊和投放高度，吊篮顶部安装快速释放装置，通过相应的控制系统实现快速投放吊篮和试验件的功能。在水池与起吊装置之间设置导轨，吊篮与导轨接触处采用轮子设计，吊篮投放后将沿导轨下坠，从而控制试验件的入水姿态。

吊篮具备可以承受垂向着水冲击载荷及侧向载荷的能力，吊篮上设置有配重安装点，通过设置配重质量及配重位置得到试验件不同质量状态下的试验条件。

吊篮四周布置加速度传感器，试验件从规定高度下落，以相应速度坠入下方水池。

3.2 试验参数

金属平板为0.8 mm铝合金薄板，尺寸为400 mm×400 mm。结构总质量为50 kg，入水速度为2 m/s。在距薄板中心r=50 mm 处布置应变片，吊篮处布置加速度传感器。

3.3 结果分析

典型金属结构着水后的加速度响应、应变响应如图4、图5 所示。由图4 可知，金属平板入水大约5 ms 后，加速度与应变达到峰值，随后迅速衰减，并在零点附近做周期振荡。且加速度响应和应变响应的仿真曲线均与试验曲线基本保持一致。结果表明，采用SPH-FEM 法进行金属板入水冲击分析可以真实地反映结构的冲击响应特性。

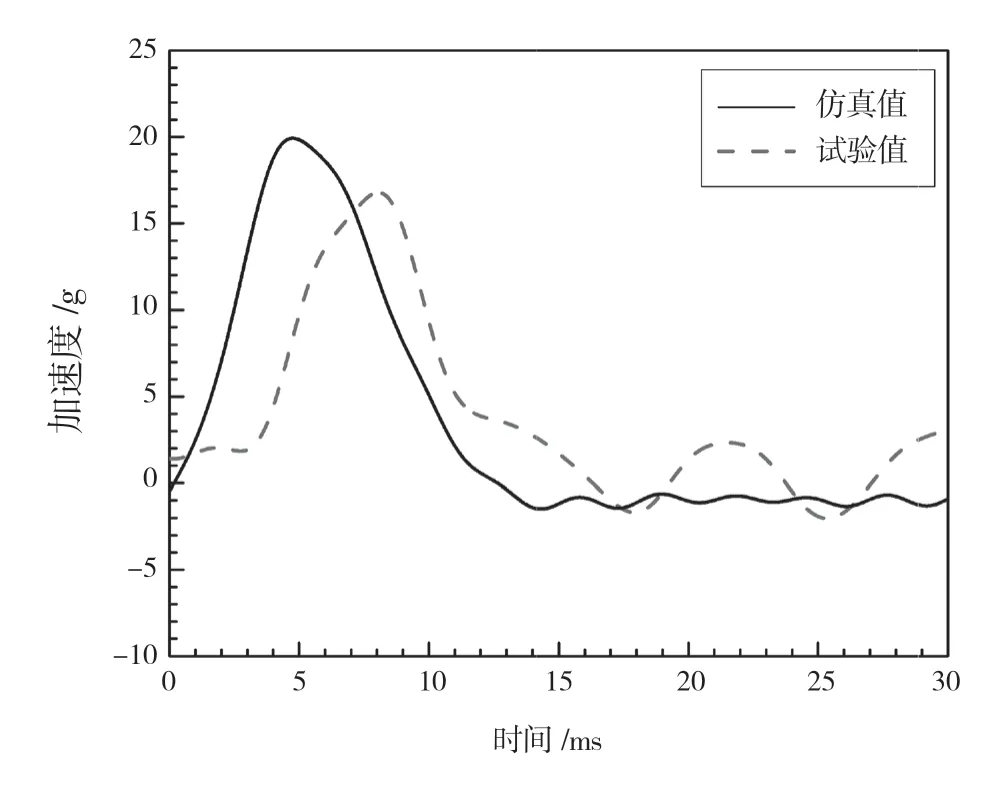
图4 典型金属结构加速度响应

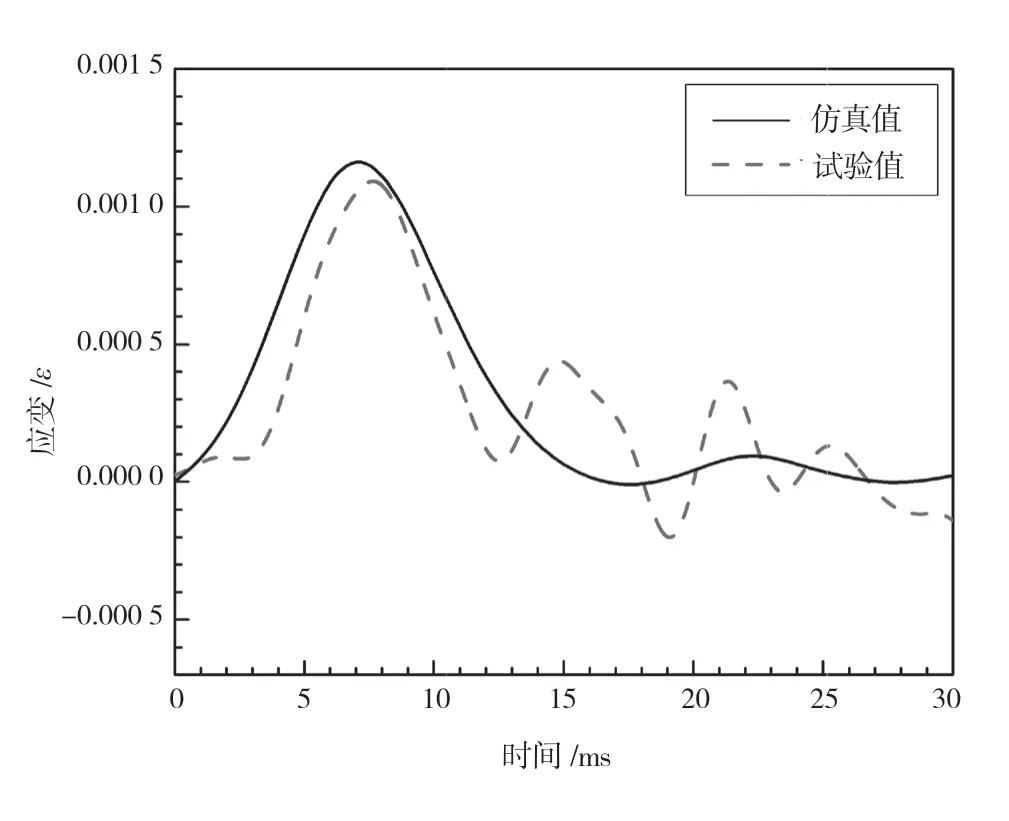
图5 典型金属结构距平板中心r=50 mm 处的应变响应

由图4 可知，金属板加速度仿真值为17 g，试验值为17 g，结果的误差为0%。由图5 可知，距薄板中心r=50 mm处应变仿真值为0.001 1 ε，试验值为0.001 15 ε，结果的误差为5%。上述数据表明，该文所用仿真模型可以准确地描述结构的冲击响应特性。

4 结语

该文建立了金属板及其支撑结构、水体以及空气的有限元模型，采用SPH-FEM 流固耦合方法对直升机典型金属结构进行入水仿真分析，相关结论如下：1）结构加速度仿真值及应变仿真值与试验值相比，误差小于或等于5%，表明该文所用仿真方法具有较高的准确性。2）结构加速度与应变响应在结构入水冲击初期达到最大，随后迅速衰减，仿真曲线与试验曲线变化趋势一致。3）该文所用的仿真模型与仿真方法具有较好的可行性和较高的准确性，能够为后续直升机整机入水仿真分析奠定基础。