考虑内腔空气影响的高速磁浮轨道箱梁日照温度场研究
2022-03-12王胤淇滕念管
王胤淇 滕念管
上海交通大学船舶海洋与建筑工程学院,上海 200240
高速磁浮列车运行时车体与轨道间的间隙为8~12 mm,因此,对轨道梁的施工精度、挠度变形、动力特性要求高。现阶段一般采用具有较大刚度和抗扭转性能的混凝土箱梁作为轨道梁的基本形式,可根据实际需求改进得到异形截面梁、梁上梁、叠合梁等[1]。
由于混凝土导热性差,混凝土箱梁在外界环境中受太阳辐射时易产生较大温度梯度,引起变形,而高速磁浮轨道梁由温差引起的挠度需控制在L/6 500(L为跨度)。因此,需要精确掌握高速磁浮轨道梁在外界环境下的温度分布。王效通[2]采用矩形单元有限元法对单室混凝土箱梁的日照温度效应进行了分析;彭友松[3]探究了桥梁方位角,箱梁翼缘悬臂长度、腹板高度对箱梁温度效应的影响;孙若晗[4]采用曲线拟合箱梁实测温度数值的方式,建立了多室混凝土箱梁的二维温度梯度曲线。Mirambell等[5]研究了箱梁横截面几何形状对箱梁温度分布的影响;Abid等[6]利用仪器测定分析了包括气温、太阳辐射、风速等条件对箱梁在太阳辐射下温度分布的影响,利用经验公式预测混凝土桥梁的竖向和横向温度梯度。但是,在上述研究中箱梁内腔空气均是按照常温进行简化处理,没有考虑箱梁内腔空气温度变化对箱梁整体温度分布的影响。
本文基于密闭空腔内部空气对流换热的规律,在考虑箱梁内腔空气变化的前提下,以上海浦东地区的环境条件为背景,研究一种组合式高速磁浮轨道箱梁的温度场分布,并根据TB 10092—2017《铁路桥涵混凝土结构设计规范》和国外相关规范拟合了箱梁横向和竖向的温度梯度曲线,最后对比该轨道箱梁的最大温差与TB 10092—2017中的温差限值。
1 梁体热分析基本原理
1.1 热传导理论
混凝土轨道箱梁截面面积大且为变截面,梁体热传导过程复杂。箱梁上任意一点的温度T与其所处的位置(x,y,z)和时间t的函数关系[7]为

轨道梁梁体结构材料主要为C50混凝土,在热传导计算中假定梁体满足均匀性、连续性、各向同性三项条件。根据Fourier热传导理论,内部无热源时热传导方程[7]为
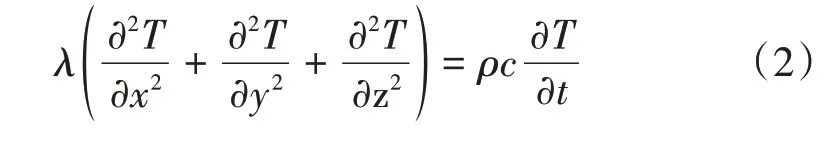
式中:λ为导热系数,W/(m·K);ρ为材料密度,kg/m3;c为材料比热容,J/(kg·K)。
热传递主要有热传导、对流传热、辐射传热三种传热方式。工程中常见的换热计算边界条件有三种。
第一类边界条件是已知物体边界上的温度或温度函数,即

式中:TΓ为箱梁边界温度;Tw为箱梁边界上已知的温度;f(x,y,τ)为箱梁边界上已知温度函数。
第二类边界条件是已知热流密度,即

式中:n为表面竖向矢量;qs为边界上单位时间单位面积通过的热量。
第三类边界条件是已知物体表面换热系数和外界环境温度,即

式中:h为物体表面换热系数;Ta为外界环境温度。
混凝土轨道箱梁在外部环境下主要受太阳辐射、对流换热的影响。根据梁体与外界传热的特点,太阳辐射可转化为第二类边界条件,对流换热可以转化为第三类边界条件,则梁体的换热边界条件可以表示为
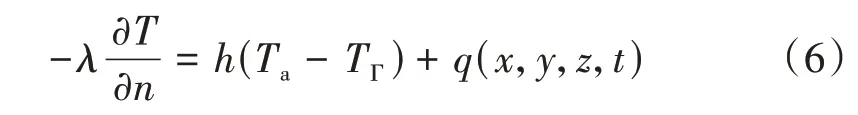
式中:q为太阳辐射热流密度。
1.2 流体热控制方程
混凝土轨道箱梁内腔气体传热遵循质量守恒、动量守恒、能量守恒定律。
质量守恒定律可由连续性方程[8]表示,即
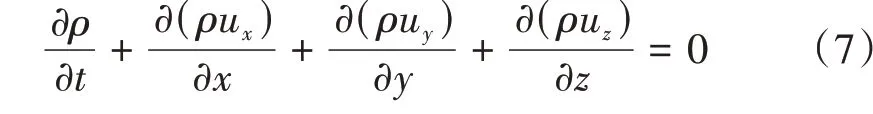
式中:ux,uy,uz分别为x,y,z三个方向的速度分量;ρ为流体质量密度。
动量守恒即内腔空气在x,y,z三个方向上满足牛顿第二定律,可用动量方程[8]表示,即
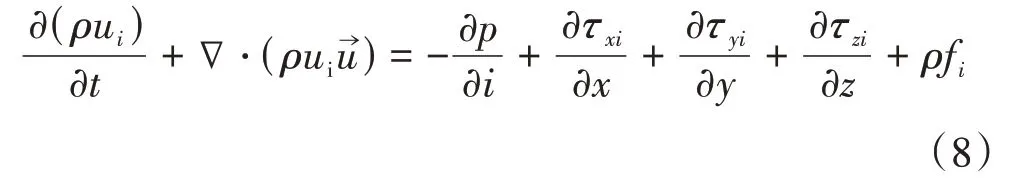
式中:i代表x,y,z三个方向;p为流体微元体上的压强;ui为i方向的速度分量;u→为速度矢量;τij为作用于微元体上i向表面上的j向剪切力分量;fi为作用在微元体上的体积力。
箱梁内腔空气在热传递中满足能量守恒定律,调用能量方程,即微元体中能量的增加率等于流入的净热流通量加上质量力和表面力对微元体所做的功[9]。能量方程为
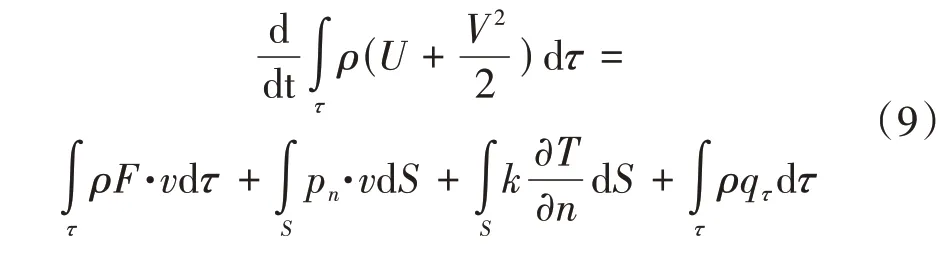
式中:U为单位体积流体内能;V为单位体积流体速度;τ为体积;F为作用于微元体的体积力;S为微元体的表面积;pn为微元体表面压强;v为单位时间移动距离;k为热传导系数;qτ为单位体积的热流密度。
2 温度场数值模拟
2.1 组合式轨道梁
传统磁悬浮轨道梁由功能件和混凝土主梁通过预埋件连接,整个梁体需在工厂制作完成之后转运到施工现场,过程复杂,成本较高。组合式轨道梁上部分为工厂预制的功能梁(即承轨梁),下部分为现场浇筑的承重梁,其横截面见图1。此种结构既能满足轨道梁的强度设计要求,又能加快施工进度,提高施工精度。现阶段国内并无高速磁浮大型轨道箱梁,本文结合CJJ/T 310—2021《高速磁浮交通设计标准》和TB 10082—2017《铁路轨道设计规范》,提出一种适用于高速磁浮的组合式轨道梁。
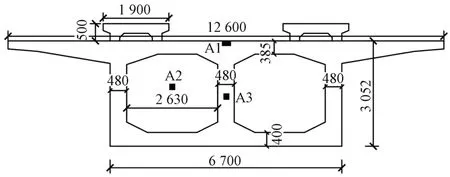
图1 组合式轨道梁横截面(单位:mm)
2.2 有限元模型
采用ANSYS中workbench子模块Geometry建立轨道梁三维有限元模型,用Mesh模块划分单元网格,空气部分采用四面体基本模块,混凝土部分采用六面体基本模块,见图2。使用有限元分析模块Fluent对模型施加边界条件和材料属性定义,进行瞬态热计算。在材料属性定义中,梁体选用C50混凝土作为基础材料,根据TB 10092—2017,混凝土密度取2 400 kg/m3,导热系数取1.758 W/(m·℃),比热容取916.7 J/(kg·℃)。箱梁内部腔体空气按照Boussinesq近似假定[10]进行分析,即密度的变化并不显著改变流体的性质,空气密度取1.128 kg/m3,热膨胀系数取0.003 2。
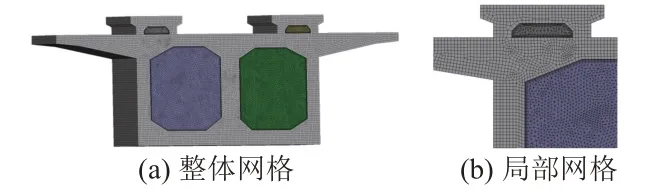
图2 网格划分
2.3 边界条件
为更好地探究日照对单箱双室混凝土箱梁的温度效应,假定轨道梁呈南北朝向,且周围环境无任何外界遮挡。以上海浦东地区为基准,所在位置北纬31.22°,东经121.54°。统计2011—2020年上海浦东地区7月、8月日平均最高最低气温后,选取最不利气温即2017年7月气温作为基础数值,当月日最高气温均值37℃,日最低气温均值28℃。该地区七月最高气温Tmax出现在15:00,日最低气温Tmin出现在03:00。将一天之间的温度变化用正弦函数表示为
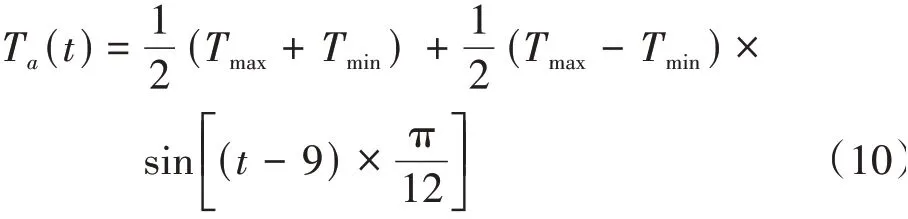
式中:Ta(t)为随时间变化的外界环境温度。
梁体所受太阳辐射主要由太阳直射、空气散射和地面反射三部分构成。根据太阳常数、太阳高度角、太阳方位角计算出太阳辐射值;太阳高度角、太阳方位角可根据太阳时角、太阳赤纬以及轨道梁所在地的经度和纬度计算获得。梁体各表面在不同时刻的太阳辐射值不同,为考虑翼缘的遮挡效应将左右腹板按高度分成三部分,为考虑功能梁的遮挡效应将顶板分成三部分进行考虑。对梁体各表面所受辐射值进行独立计算,得到梁体各表面的日照辐射值见表1。其他时刻梁体各表面日照辐射值为0。
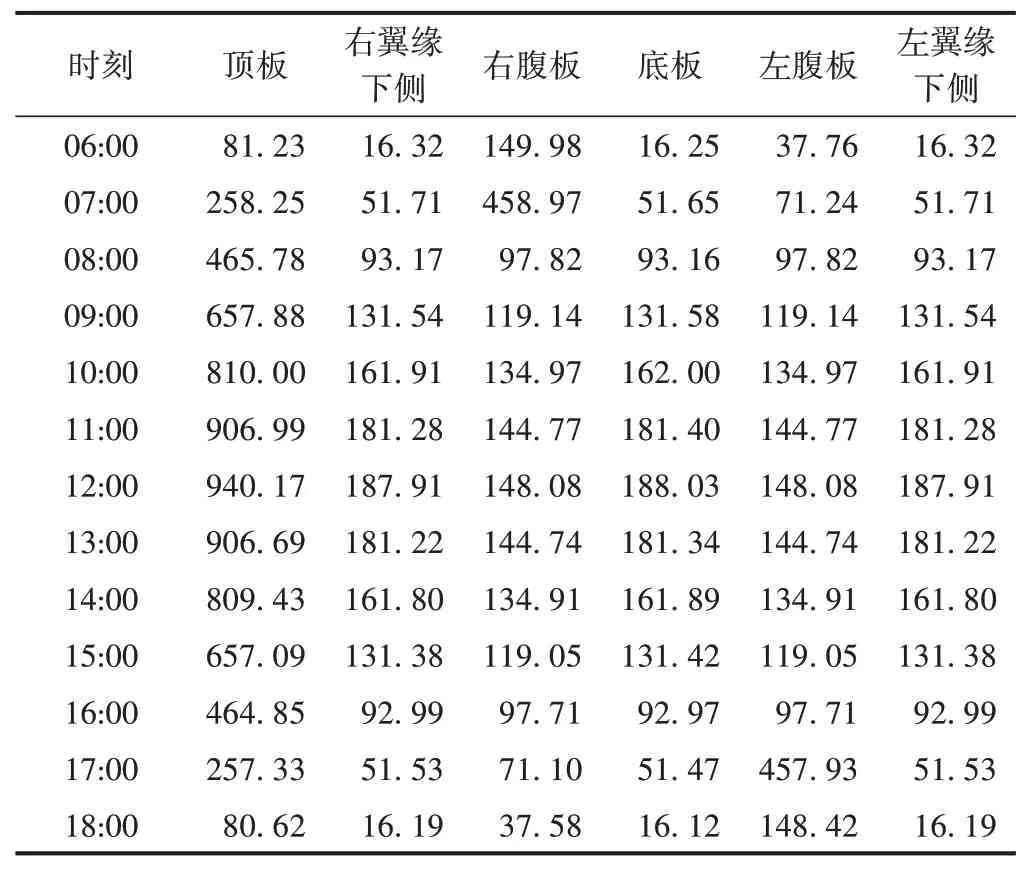
表1 各时刻日照辐射值 W·m-2
梁体与外界的热交换过程可转化为第三类边界条件,此时物体表面换热系数h为辐射换热系数hr与对流换热系数hc之和。
辐射换热系数hr是表示介质之间通过长波辐射方式进行的热交换速率。由辐射定律可得混凝土表面的辐射换热系数为Ta的函数[11],即

对流换热系数hc与梁体材料、表面方位、外界风速、环境温度等多种因素有关,其中外界风速影响较大。对于组合式轨道梁其各表面对流换热系数可表示为外界风速v的函数[11],即顶板hc=3.83v+4.67;腹板hc=3.83v+3.67;底板hc=3.83v+2.17。
浦东地区在研究时间段的大气温度平均值为32.5℃,代入式(11)得到辐射换热系数为6.039 W/(m2·℃)。根据《中国建筑热环境分析专用气象数据集》,取上海夏季平均风速3.5 m/s,可得顶板、腹板、底板的对流换热系数分别为18.075、17.075、15.575 W/(m2·℃),进而得到顶板、腹板、底板的换热系数分别为24.114、21.614、23.114 W/(m2·℃)。
3 计算结果分析
3.1 箱梁整体温度
分析时将箱梁初始温度设置为环境温度最低值28℃,将太阳辐射值转化为温度边界值加载到箱梁各表面上进行24个周期的迭代计算,模拟在该环境下24 d内箱梁的温度分布情况。取轨道梁特征节点进行温度分析,节点具体位置参见图1。节点温度和环境温度时程曲线见图3。可知:箱梁整体温度在前12 d随时间的推移呈波动上升状态,12 d后趋于稳定;节点A2的温度12 d后在36℃左右波动变化,温度接近环境温度最大值。
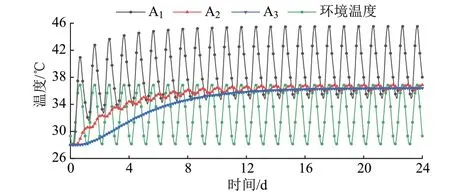
图3 特征节点和环境温度时程曲线
3.2 箱梁内外温度场
根据图3可知在12 d后箱梁温度分布变化趋于稳定,因此选取第13天的温度分析轨道梁的温度场,见图4。可知:箱梁外表面温度变化受日照辐射变化影响大,梁体内部温度变化受日照辐射变化影响较小;箱梁内腔空气温度的特点为上部温度较高,整体温差较小,且整体温度变化滞后于外部气温变化。
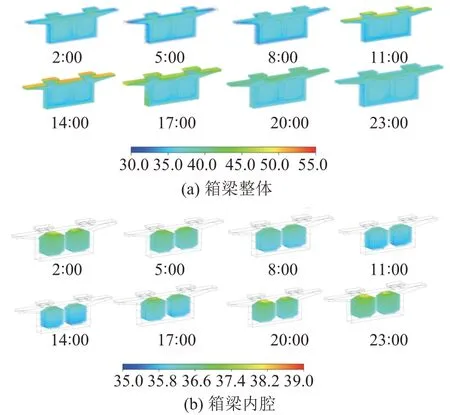
图4 不同时刻箱梁温度场云图(单位:℃)
3.3 节点温度
为研究单箱双室箱梁竖向和横向温度分布规律,以及梁体内腔空气对梁体整体温度分布的影响,选取箱梁部分节点(图5)对箱梁温度变化情况进行分析。其中,节点N11—N15距离顶板0.1 m,节点N16—N20距离底板0.1 m,节点N21—N27距离底板1.5 m。

图5 节点布置(单位:m)
腹板温度时程曲线见图6。可知:①节点NU1的温度随时间的推移变化幅度最大,受日照辐射影响最大,单日变化幅度达20.8℃;腹板上下部分因顶底板与环境换热,温度变化明显高于腹板中部。②中腹板上部节点和下部节点变化与右腹板相近,受日照辐射和外部气温影响大;节点N7,N8,N9因处于梁体内部,受外部温度变化影响小,温度变化幅度较小。
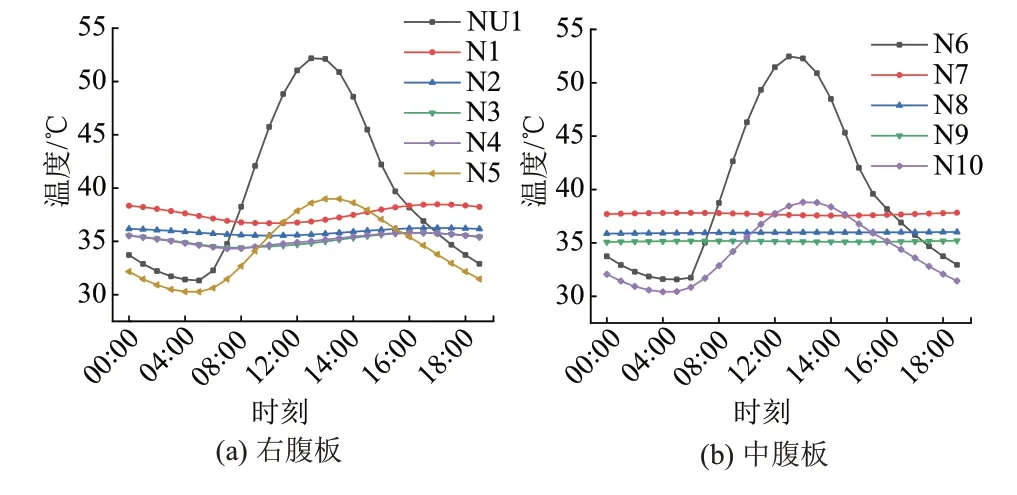
图6 腹板温度时程曲线
箱梁顶底板温度时程曲线见图7。可知:①节点N12,N14温度变化幅度小,因此这两个节点不与外部环境直接换热;节点N11,N15温度变化一致,滞后于节点N13,这是由于节点N13位于顶板中部,梁体内部存在保温效应,初始温度较高。②节点N16单日温度变化幅度达到14.7℃,最高温度出现在16:00;节点N20单日温度变化幅度达到10.1℃,在08:00出现最高温度值39.7℃。③与图3对比,节点N17—N19环境温度变化趋势相近;底板两端节点受日照辐射影响大,中间节点主要受外界环境温度影响。
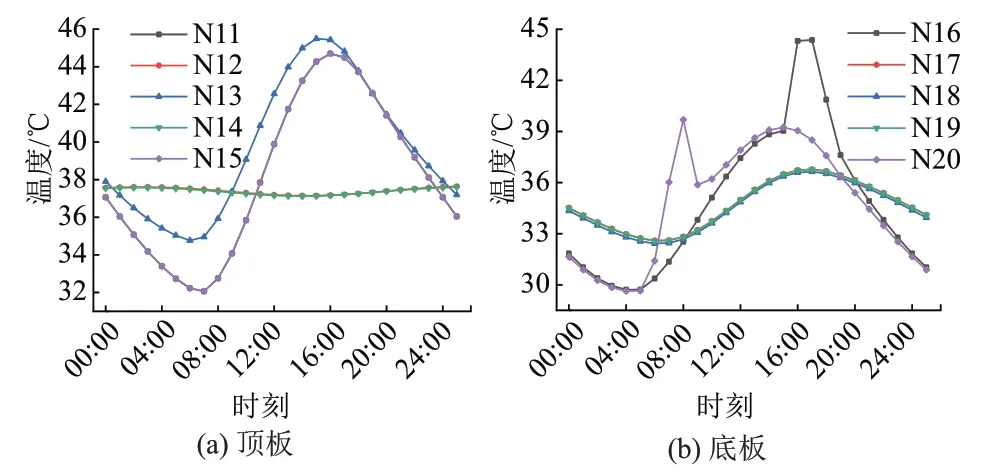
图7 顶底板温度时程曲线
箱梁中部温度时程曲线见图8。可知:箱梁中部温度变化幅度较小,且整体温度接近环境温度最大值。
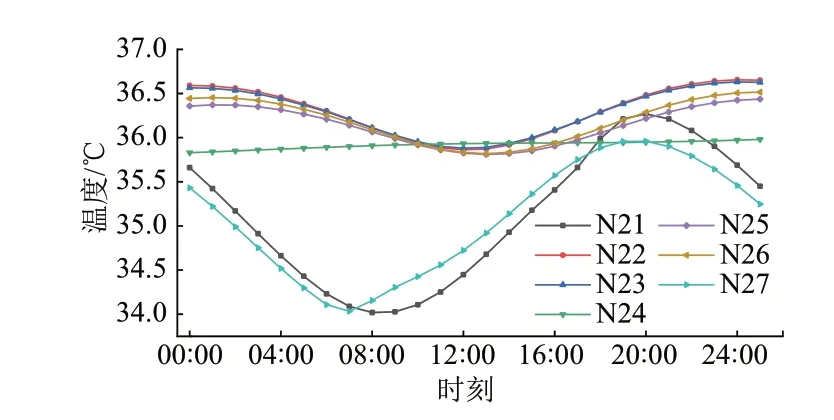
图8 箱梁中部温度时程曲线
3.4 截面竖向温度梯度
根据右腹板温度时程曲线选取当天代表性时刻04:00,22:00以及全天温差最大时刻14:00分析腹板竖向温度梯度,见图9。可知:①各时刻左中右腹板竖向温度梯度变化趋势保持一致,在承重箱梁顶板1.4 m范围内和底板0.3 m范围内的腹板温度变化迅速,位于中间部分的腹板温度变化平缓,且腹板竖向温度梯度在箱梁混凝土与内腔交界处温度变化明显。②在04:00,中腹板温度较高,中腹板在箱梁顶板向下0.33 m处温度达到最大值,左右腹板是在功能梁顶部向下0.30 m处出现温度最大值,这是因为箱梁内腔空气的保温效应导致箱梁内腔空气温度高于外部环境温度,且内腔空气温度上部较高,下部较低。③在22:00,箱梁中腹板底部温度低于两侧腹板底部温度,左腹板底部温度高于右腹板底部温度,原因是下午箱梁左侧腹板吸收的日照辐射值大于右侧腹板,混凝土传热较慢引发了滞后效应。

图9 箱梁竖向梯度
3.5 截面横向温度梯度
根据图7可知,在08:00、16:00顶板、底板温差较大,在22:00温度下降较快,得到这3个时刻下的顶板、底板横向温度梯度见图10。可知:①在08:00,箱梁顶板接触功能梁部分的温度较高,箱梁内腔对应的顶板温度高于左右翼缘处顶板温度;左右腹板对应的底板温度低于空腔对应的底板温度。②在16:00,顶板右端温度低于中间温度,顶板左端温度最高;箱梁顶板与功能梁直接接触部分的温度梯度显示为两个凹槽,这是因为该部分顶板无法被太阳直射,且混凝土传热较慢,所以温度较低;底板左端受太阳直射,底板左端温度高于底板右端和中部。③在22:00,箱梁内腔所对应的顶板温度高于腹板对应的顶板温度,顶底板两侧温度较低,这是因为箱梁两侧与外部环境接触散热较快,箱梁内部混凝土和内腔空气散热较慢。④在各个时刻,箱梁顶底板在内腔和腹板交界处都有一定的局部温度变化,这是由于箱梁内腔的保温效应,导致内腔所对应的顶底板部分温度相对较高。
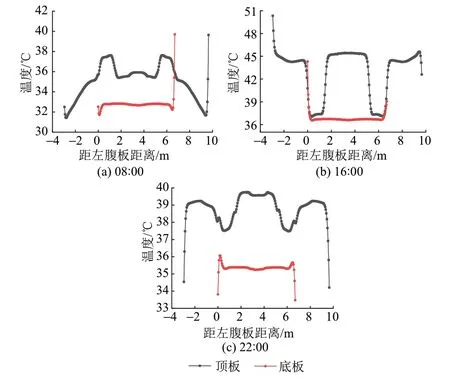
图10 箱梁横向温度梯度
3.6 温度梯度拟合和温度梯度计算结果对比
参考新西兰规范中提出的在箱梁顶部向下1.2 m范围内和箱梁底部向上0.2 m范围内施加不同温度梯度荷载的方法[3],根据TB 10092—2017对箱梁横向和竖向温度梯度上部和下部变化剧烈部分进行指数拟合,得到箱梁竖向温度梯度在上部1.4 m范围内的表达式为T=15.85e-6.71y,下部0.4 m范围内的温度梯度表达式为T=4.67e-10.79y。对底板采取相同方式进行拟合得到底板靠左端0.3 m的温度梯度表达式为T=7.63e-16.19x,右端0.3 m的温度梯度表达式为T=3.76e-3.14x,温度梯度拟合曲线见图11。计算得到竖向和横向温差极值分别为15.85、7.63℃,小于TB 10092—2017中的竖向温差限值20℃,横向温差限值16℃。

图11 温度梯度拟合曲线
本文中采用有限元软件对单箱双室混凝土箱梁进行分析所得到的箱梁内腔气体温度以及横向和竖向温度梯度与文献[12]实测结果吻合,说明在考虑箱梁内腔空气影响的前提下计算得到的梁体温度场分布结果符合实际情况。
4 结论
1)在日照辐射影响下,箱梁截面外表面的温度变化与日照辐射强度相关性强,箱梁内部温度变化较小,箱梁整体温度变化相对于气温有一定的滞后性。
2)在长期高温环境下,箱梁内腔气体温度接近环境温度最大值,受日照辐射影响较小。对长时间处于高温环境下的大型箱梁进行温度效应分析时,需要考虑箱梁内腔空气传热的影响。
3)在考虑箱梁内腔空气传热效应影响后,箱梁的腹板竖向温度梯度在箱梁混凝土与内腔交界处局部温度变化明显;箱梁底板在内腔和腹板交界处所对应的局部有一定温差。
4)该轨道箱梁整体竖向和横向温度梯度峰值比我国现用规范值偏小,且竖向和横向温度梯度在另一侧都存在反向温差,与规范中的单向温差变化不同。
