基于隶属函数的多机械臂系统协调控制方法

李星星

（郑州西亚斯学院 教育学院，郑州 451150）

0 引言

目前，机械臂系统被广泛应用于工业生产制造领域，其具有灵敏度高、运行灵活、可靠性高、负荷能力强等特点，可以完成复杂度高、强度大的工业作业任务。机械臂常在一些特殊环境中工作，受复杂环境影响，其运动轨迹会受到干扰，导致其工作效率大幅下降[1]。因此，对机械臂运动轨迹控制非常重要，这也是整个系统运作的关键环节。

当前，多机械臂系统协调控制成为热门研究话题。例如文献[2]中提出了杆距避碰距离指标建模法。设避碰距离指标为机械杆之间的最小距离，利用权值函数建立模型，依据距离函数规划躲避障碍物动态运行轨迹，降低机械臂在作业过程中受碰撞几率，达到系统协调控制效果；针对机械臂受到振动导致轨迹偏离现象，文献[3]中将轨迹优化法和时间倒装法结合建立无残余振动轨迹控制法。在分析动力学模型基础上，建立状态约束方程，规划前向和反向两条轨迹，并将两条轨迹结合在一起。最后，利用轨迹跟踪控制器使机械臂系统按照规划的轨迹运行，克服残余振动影响。

基于上述研究，本文提出一种基于隶属函数的多机械臂系统协调控制方法。在对多机械臂系统展开运动学分析的基础上，采用分层优先级结构确保系统优先执行机械高的任务，然后通过傅里叶变换获取机械臂振动特征和振动频率，并在划分控制范围的基础上，根据机械臂在旋转角、平移角方向上的隶属度计算每个关节速度矢量，再根据优先执行级别实现对多机械臂系统的协调控制。

1 多机械臂系统运动学逆解分析

运用运动学逆解可以实现对关节位置限制的分析，从而更好地为后续的运动控制奠定基础。因此为了深入了解多机械臂系统的运行规律，本研究以双机械臂系统为例，构建机械臂运动学模型。双机械臂系统结构如图1所示。

图1 双机械臂系统结构示意图

双机械臂两轴分别为A和B，式(1)为双机械臂系统末端速度量定义公式：

式(1)中，xRd表示机械臂位移，PR表示机械臂末端执行器相对位置，φR为机械臂末端执行器的相对方向，tRd表示机械臂末端执行器运动时间。

在双机械臂系统中，关节总数可以从机械臂运动关系中得出：n=2nj，其中nj为各机械臂关节数。然后假设机械臂A和B的雅克比矩阵分别为JA、JB，这两个值的大小取决于参考系数值，此时需要将雅克比矩阵变换成对角矩阵，用旋转矩阵定义转换后的矩阵，过程如下：

式(2)中，AK、qBK分别为两个操纵器nj维关节列向量，S(PR)表示斜对称矩阵；R表示变换矩阵，末端笛卡尔坐标系分别为Ae和Be，整体笛卡尔坐标系为Tf。

以机械臂A为例，转换后的矩阵与双机械臂系统末端速度量之间的关系如下：

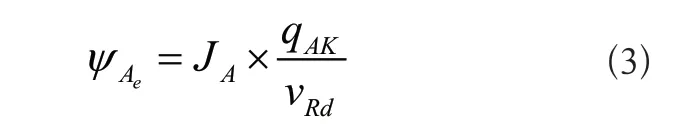
式(3)中，qAK=[ψAc]T。在此基础上，基于雅克比矩阵JA与其伪逆矩阵J-A，通过零度空间梯度投射法可以求出最适合的逆解[4]，过程如下：

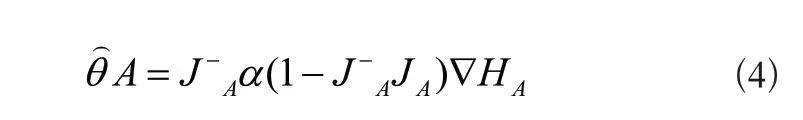
式(4)中，a表示机械臂末端操作系统角速度，HA表示去掉极限关节值后的其余附加规则函数，当H(0)取最大值时，a为正数；当H(0)取最小值时，a为负数，该值由机械臂关节力矩和速度决定。

2 多机械臂系统任务优先级分析

多机械臂系统在作业过程中，依据任务的重要程度分为主、次要任务，主要任务执行优先级高于次要任务。雅克比矩阵秩受机械臂关节数量n和具体执行任务l的影响，其值决定最大同时处理任务量。为此，本研究运用优先级分层结构避免多机械臂任务间的冲突问题。

为了规避优先级高的任务受低等级任务影响，把低等级任务放到零空间Nk中，确保高等级任务完成质量。假设x1、x2、x3为不同的任务，它们之间的优先级为x3＞x2＞x1，由此可以获得多机械臂系统联合速度矢量如下：

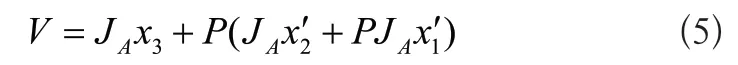
式(5)中，P是零空间的正交投影矩阵[5]。在雅克比矩阵的多机械臂系统内，应控制末端执行器执行高优先级任务，再通过控制运动操作执行低优先级任务。因此，根据雅克比矩阵可以将多机械臂控制器输出过程表述为如下形式：

式(6)中，Kk表示机械臂反馈位置偏移的增益系数。

由于机械臂的运动速度较快，因此，应控制器优先执行关节限制和障碍物回避任务；对于机械臂运动速度逐渐减慢情况，附加工作优先级别提高，此时关节冗余运动优先执行其他工作，从而合理利用了机械臂关节的冗余度。

蒲琳笑着不由自主地搂住张盈盈，半天却不知道说什么，想起以前她赌气和张盈盈说起的摘星星的话，就说：“我们想摘的星星是什么？”

3 基于隶属函数协调控制多机械臂系统

机械臂的主轴是核心控制部件，在实际作业时，受到周围环境、装配材料、机器故障等影响，会产生控制系统质量不平衡现象，导致主轴振动，运行轨迹偏离预设路线，工作效率和质量下降。因此，在进行机械臂协调控制前需要抑制主轴不平衡振动。

准确提取主轴振动特征是抑制不平衡振动的前提，为此，本文采用全相位数据预处理算法提取振动特征信息。首先输入离散型信号，长度为(2N-1)，然后利用卷积窗wc的数据加权法对信号进行处理，再将每隔N个单元的加权数值叠加，导出N个值。在对数据进行预处理后，通过傅里叶变换频谱分析功能，准确获取机械臂的位置及其振动幅度。式(7)为时间序列x(0)的N点N维向量：

将每组的x(0)放到首位，就可以获得另外一组N点N维向量：

将x(0)加在一起，然后取平均值，这时就可以获得全相位数据向量：

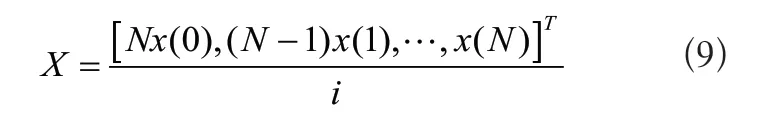
式中，i为机械臂关节数量。上述过程可以准确获取机械臂振动信号特征，然后依据特点处理振动信号，使机械臂振动相位更准确，在一定程度上优化后续系统控制效果。

基于傅里叶变换处理机械臂的振动影响后，利用隶属函数实现对多机械臂系统的协调控制。多机械臂系统旋转角、平移角方向上的隶属度函数如图2所示。

图2 旋转角、平移角方向上的隶属度曲线

观察图2可以看出，旋转角和平移角方向上的隶属度曲线呈规律性变动。其中，正方向表示向右运动、负方向表示向左运动。机械臂每个关节速度矢量为：

式(10)中，HA和HB表示通过两个加权平滑对角矩阵WA和WB构成的控制增益，qTA和qTB表示ng维向量。β为关节摆动极限范围。通过控制关节位置可以使机械臂运动轨迹更平滑，减少关节不连续信号。

式(11)中，Et+1、Et分别表示机械臂在第t+1和t时刻正方向上的避障轨迹幅度，ft+1、ft分别表示机械手在第t+1和t时刻负方向上的避障轨迹幅度，δ表示控制参数。

4 仿真实验与结果分析

为了验证基于隶属函数的多机械臂系统协调控制方法的实际控制效果，以图1中的双机械臂系统为对象开展仿真实验。设置实验时间为50s，机械臂A、机械臂B的转动惯量分别为VA、VB，初始位置分别为fA、fB，两机械臂直接的连杆长度为U，机械臂A、机械臂B的质量分别为mA、mB，轴中心到转动关节距离分别为rA、rB。表1为机械臂参数的数值。

表1 机械臂参数数值

按照表1的参数值，利用本文方法对双机械臂系统发布一次指令对实施控制，然后记录机械臂关节的实际弧度，并将记录结果与理想状态下的关节弧度展开对比，用于初步验证本文方法对多机械臂系统协调控制的有效性。实验结果如图3所示。

图3 机械臂控制效果对比

观察图3所示结果可以看出，双机械臂系统中，在本文方法的控制下，机械臂关节的弧度曲线与理想状态值基本一致，两者之间的差距非常小，说明本文方法能够有效约束双机械臂系统关节的位置，从而达到较好的控制效果。

在此基础上，构建与实际操作空间同等比例的空间坐标系，从而直观地观察方法的控制效果。实验设计如下：

实验轨迹以双机械臂系统末端关节的轨迹为准。其中，机械臂A 的起点坐标为（1.2，0.2，1.5），终点为（1.4，0.8，0.4）；机械臂B 的起点坐标为（0.6，1.5，1.5），终点为（0.2，1.9，1.0，）。

空间中存在多个障碍物，双机械臂系统需要躲避这些障碍达到终点，从而具体观察测试本文方法的控制效果。实验结果如图4所示。

图4 双机械臂系统避障控制轨迹

观察图4 所示结果可以看出，机械臂A 的运动轨迹坐标依次为（1.2，0.2，1.5）→（1.6，0.4，1.2）→（1.5，1.0，0.7）→（1.3，0.6，1.3）→（1.0，0.7，0.5）→（1.4，0.8，0.4）；机械臂B 的运动轨迹坐标依次为（0.6，1.5，1.5）→（0.9，1.2，1.3）→（0.6，1.5，0.7）→（1.0，1.4，0.6）→（0.4，1.8，1.2）→（0.2，1.9，1.0，）。在应用本文方法对双机械臂系统实施控制后，机械手末端关节能够准确躲避障碍物，且其运动轨迹与障碍物之间存在一定大小的位移距离，从而有效保障了双机械臂系统的移动安全性。

5 结语

机器人技术随着科技水平不断提高，具备了高等级智能性。机械臂是高精度人工智能整合体，可以模仿人类手臂进行抓取物体和机械吊装，完成高强度作业，应用日益广泛。在实际操作过程中，机械臂常常在复杂环境中工作，受机械振动和湿度影响运动轨迹会受到干扰，不能按照预设值运行。针对这种情况，本文提出一种基于隶属函数的多机械臂系统协调控制方法。将成本函数梯度设置成最低优先级任务，把优先执行级别分配给关键关节，运用排斥关节速度把每个关节限制在规定范围内，固定好每个关节位置，以此协调控制多机械臂系统。仿真对比实验结果验证了本文算法的多机械臂系统协调控制效果好。