基于物理观念 突出问题的物理本质——“硬币悖论”问题的再探究

李德林

（山东省寿光中学，山东 潍坊 262704）

1 问题再现

如图1所示，已知小圆的半径为r，大圆的半径是小圆的3倍，小圆绕大圆做匀速滚动（大圆静止不动，两圆无相对滑动）.当小圆绕大圆转一圈时，小圆自转几圈？若此过程只需1s，求小圆圆周上的点绕其圆心转动的线速度为多少？

图1

相似的问题曾经出现在1982年的美国的数学高考卷中，并且闹出了乌龙事件，《纽约时报》对这件事进行了报道［1］，在当时引起了轰动，因为参与考试的30多万人里只有3人答对，本题给出了1.5圈、3圈、6圈、4.5圈、9圈共5个选项，正确的答案是4圈，就连出题人也做错，给出的5个选项里没有正确答案，出题方美国大学理事会事后声明，出题方的答案是错的.

这个问题在数学上叫“硬币悖论”，将两枚相同的硬币整齐的摆放，将上面的硬币沿着下面的硬币滚回原来位置，你会发现上面运动的硬币实际转了两周，而不是我们想象中的一圈，这种反直觉的现象被称为“硬币悖论”.

2 基于物理观念和思维，探究问题本质

文献［2］从不同的角度，采用了“化曲为折”、质心（圆心）观点、实践验证、数学绘图软件作图等四种方法对这一问题进行了分析论证，其中 “化曲为折”的方法把圆周等效成多边形，用的是一种等效思想，等效思想是分析物理问题时常用的一种思维方法，目的是把复杂的问题简单化，抽象的问题具体化，文献［2］中“化曲为折”的方法，反而使简单的问题复杂化，直观的问题抽象化，费时费力，特别是小圆在大圆内测滚动的情况，数学证明更为繁琐，不利于学生理解小圆沿着曲线滚动的本质特点.

问题的实质在于小圆绕大圆公转的过程中，即使没有滚动小圆自身也发生了转动，学生理解了这一点，问题就容易解决.可以先分析小圆沿着大圆滑动（没有滚动）的情况，如图2所示，A点为小圆上的一个固定点，假设小圆总是和大圆在A点接触沿着大圆滑动一周，图中标出了几个特殊位置，可以看出小圆沿着大圆滑动了一圈小圆也自转了一圈，也就是小圆绕大圆的公转周期与小圆的自转周期相同.这可类比为一个同学沿着一个圆形操场跑步，假设某一时刻面向南，经过了半圈变成了面向北，身体绕质心转动了半圈，再经过半圈又成了面向南，也就是沿着操场跑了一圈身体也自转了一圈.

图2

理解了上述规律，当小圆沿着大圆滚动（无滑动）时，小圆的自转圈数就水到渠成容易解决，先算出小圆相对大圆的滚动圈数，小圆的自转圈数就是小圆相对大圆的滚动圈数加1，为什么是加1而不是减1，由图2可以看出，小圆沿着大圆的公转方向和小圆的自转方向一致，当小圆沿着大圆顺时针滚动时，小圆的自转方向也是顺时针.

如果小圆沿着大圆的内侧滚动，小圆沿着大圆的公转方向与小圆的自转方向相反，当小圆沿着大圆顺时针滚动时，小圆的自转方向为逆时针（如图3），因此小圆的自转圈数就是小圆相对大圆的滚动圈数减1.

图3

此方法原理简单、省时省力，透过现象看本质，避免了建立复杂的数学模型和繁琐的数学证明.

3 两个圈数为什么不一样

本题中小圆相对于大圆滚动了3圈，小圆也确实自转了4圈，文献［2］分析了求小圆自转圈数的多种方法，但是两个圈数为什么不同，学生还是感到疑惑，还是不理解问题的实质.

我们说小圆沿着大圆滚动，是地面上的人看到的运动形式，显然是以地面为参考系的运动描述，而小圆自转是相对于小圆的转轴或圆心来说的，是以小圆的转轴或圆心为参考系的运动描述，题目中求小圆边缘上点的线速度也是相对于圆心的速度.因此小圆运动的两种不同描述是相对于不同的参考系来说的，小圆的滚动圈数是地面参考系内的圈数，小圆的自转圈数是圆心参考系内的圈数，而小圆的圆心相对于地面参考系又在运动，选择的参考系不同，运动形式就不一样，所以圈数不一样，学生明确了这一点才能理解两个圈数不同的本质.

4 质心（圆心）解法的理论依据

文献［2］中根据小圆的质心运动求自转圈数的方法，解法简便但是学生不理解其中的原理，文中的理论依据是，由于小圆运动的路程是其圆周上的点绕质心转动造成的，那么其圆周上的点相对于质心运动的弧长等于质心运动的路程，这样说明，学生不知其所以然，理解起来有困难.

要求小圆圆周上的点的相对于其圆心的弧长，先求其相对于圆心转动的线速度，因为存在两个参考系，需要搞清楚牵连速度、相对速度和绝对速度三者间的关系.如图4所示，设小圆圆心相对于地面速度为v1，小圆圆周上的点相对于其圆心的线速度为v2，因为小圆相对于大圆无滑动，所以小圆圆周上与大圆接触的点相对于地面的速度为0，即绝对速度为零，所以牵连速度v1和相对速度v2等大反向.因此小圆圆心运动的路程等于小圆圆周上的点相对于圆心运动的弧长，这就是根据小圆质心（圆心）运动解法的理论依据.

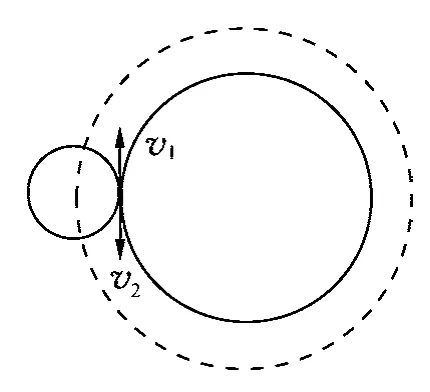
图4

这个解法可以推广到一般情况，不管小圆沿着直线滚动还是曲线滚动都成立.

5 问题拓展

古希腊著作《论力学》里面有这样一个问题，是一个让当时不少伟大的数学家感到困惑的谜题，困扰当时数学界几百年.

在轮上有两个同心圆，如图5所示，轮子滚动一周，从A点移动到B点，这时AB的距离等于大圆的周长，此时小圆也正好转过1周，并走过了AB的距离，这不表明小圆周长和大圆相等吗？

图5

图6

该问题可以建立数学模型分析，［3］但需要有较强的数学思维能力，如果基于物理观念和思维，通过构建物理模型，容易分析清楚问题的本质.因两个圆同轴转动，大圆滚动一圈，小圆的滚动圈数和自转圈数也都是一圈，在圆心参考系内，两圆圆周上的点角速度相同，设大圆、小圆半径分别为R和r，圆周上的A、C两点在圆心参考系的线速度大小分别为Rω和rω，设圆心运动速度为v0，因轮子沿地面滚动（无滑动），所以与地面接触点A点在地面参考系中速度为零，所以牵连速度v0和相对速度Rω等大反向（如图6），即v0＝Rω，对于小圆上的C点，则v0＞rω，绝对速度vC＝v0－rω.这说明小圆上的C点在地面参考系中的速度不为零，小圆不是纯滚动，在滚动的同时还有滑动，因此AB之间的距离要大于小圆的周长.小圆半径r越小滑动速度越大，当小圆的半径无限小，小圆就收缩成了轮子的圆心，就只有滑动没有了滚动.

6 结束语

双圆滚动问题，容易被现象和直觉所蒙蔽，认不清问题的实质，这样的问题如果单纯靠建立数学模型（如文献［2］中的“化曲为折”）去分析，过程会比较复杂，也认不清问题的本质；如果基于物理观念、渗透物理思维，通过建立恰当的物理模型去分析，容易看清问题的物理本质，［4，5］问题往往会迎刃而解.