塑相水田土壤参数对履带式拖拉机行驶性能的影响

曹明，龙祖熙，王永维，潘宇轩，王俊

（浙江大学生物系统工程与食品科学学院，杭州 310058）

水稻是中国的三大粮食作物之一，2020年全国水稻种植面积为3 007.6 万hm2[1]。复杂的水田土壤环境为水田机具行驶、作业带来极大的不便。履带式拖拉机因其接地比压小、通过性好，对农田压实破坏小、附着性好，故在农业生产、矿山机械和工程机械等领域中得到了广泛运用。目前，对在旱地及非道路固相土壤环境中应用的履带式动力底盘的动力学特性可以通过经验公式、仿真试验获得，如：RUBINSTEIN 基于多体动力学软件对履带式推土机进行建模，研究了推土机下陷深度、行驶阻力与土壤间的关系[2]；CHEN等为了改善履带式车辆在起伏路面上的适应性，设计了一种能够适应路面波动的履带式车辆[3]；杨聪彬等研究了履刺结构的履带板对土壤推力的影响，获得了计算履带板对土壤推力的新方法[4]；张季清等研究了微型履带式拖拉机的牵引附着性能[5]。这些研究成果对旱地履带式拖拉机设计具有重要借鉴意义。但水田土壤性质复杂多变，土壤中黏粒在湿润时具有黏附特性和塑性，是土壤颗粒中最为活跃的成分[6]，且土壤种类、含水量、密度等参数变化对水田土壤剪切特性[7]、坚实度[8]、承压特性[9]的影响极显著，对土壤的物理力学特性起决定性作用[10−11]；因此，以确定类型的固相土壤及其参数恒定条件下的研究成果不适用于水田条件下履带式拖拉机的设计。而关于水田条件下履带式动力底盘方面的研究，相关成果主要集中在对土壤的压实[12]、转向阻力[13−14]、行驶稳定性[15−16]等方面，在水田土壤参数、作业工况等对履带式水田拖拉机行驶性能影响方面的研究成果缺乏，不能在设计阶段通过全参数值仿真确定其主要性能，导致研发周期长、成本高。

为了探明塑相水田土壤参数、行驶速度对履带式水田拖拉机行驶性能的影响，本研究利用多体动力学分析软件RecurDyn 建立了履带式水田拖拉机实体模型和水田土壤模型，通过耦合仿真试验研究土壤黏粒含量、含水量、密度等参数以及行驶速度对履带式拖拉机下陷深度、行驶阻力的影响，并建立相关模型，为水田履带式拖拉机的设计与参数优化、性能评价奠定基础。

1 履带式水田拖拉机-水田土壤耦合仿真

为了研究履带式水田拖拉机在不同水田参数条件下的动力学特性，需要分别建立履带式水田拖拉机物理模型、不同水田参数的土壤力学模型，然后进行耦合仿真。

1.1 履带式水田拖拉机物理模型

以NF802 型履带式水田拖拉机虚拟样机和实体机（湖南农夫机电有限公司）的参数为基础建立履带式水田拖拉机物理模型，其主要参数如表1 所示。因履带式水田拖拉机行驶时只有行驶机构与水田土壤接触，所以将整机模型简化为行驶机构、机架及其他部件。行驶机构由支重轮、驱动轮、托链轮、引导轮、履带及张紧装置等组成，通过RecurDyn 软件工具包Trcak−LM 进行建模，然后赋予各部件的材料与质量属性、约束等。机架形状不规则，先利用三维建模软件Solid Works完成机架建模，然后无差别导入RecurDyn 软件。在RecurDyn软件中将行驶机构和机架进行装配，修改其他部件的质量，使总质量与原型机一致，同时，按原型机设定整机的转动惯量、重心等参数，完成虚拟样机建模，如图1所示。

表1 NF802型履带式水田拖拉机主要参数Table 1 Main parameters of the NF802 type tracked paddy field tractor

1.2 水田土壤力学模型

将水田土壤设置为长方体，长×宽×深分别为40 m×10 m×200 mm，采用RecurDyn 软件的Ground模块进行建模，选择标准模型中的土壤类型，依次填入对应土壤的内聚力c、内摩擦角φ、内聚力模量kc、摩擦模量kφ、沉陷系数n。其中，不同类型土壤的内聚力c、内摩擦角φ依据Coulomb强度定律计算得到[7]，内聚力模量kc、摩擦模量kφ、沉陷系数n依据Bekker模型计算得到[9,17−18]。

1.3 履带式水田拖拉机-水田土壤耦合仿真试验

在RecurDyn软件中完成水田土壤力学模型、履带式水田拖拉机物理模型建立后，设置水田土壤初始位置，使水田土壤上表面与履带底部保持很小距离，通过RecurDyn 软件添加驱动并运行，然后将履带式水田拖拉机下降至水田土壤中，在设定的土壤条件、行驶速度下进行仿真试验（图1），并同步采集速度、扭矩、整机重心位移等数据。

图1 履带式水田拖拉机-水田土壤耦合仿真试验Fig.1 Coupling simulation tests for tracked paddy field tractor and paddy soil

2 仿真试验方案

2.1 试验因素与水平

土壤质地、含水量、密度是影响水田土壤承压特性和剪切特性的主要因素，从而影响履带式拖拉机前进阻力和附着性，且在不同前进速度下阻力也不同，因此，将土壤质地、含水量、密度以及拖拉机行驶速度作为试验因素，并以黏粒含量作为土壤质地的指标。由于浙北平原区、陵盆地区、浙东盆地低山区基本覆盖了典型水田土壤类型[19]，该区域土壤黏粒含量（质量分数）为22.3%～40.2%[20]，故土壤黏粒含量设置为20.0%～40.0%；塑限在18.5%～31.5%之间，液限在49.5%～55.5%之间[20]，为研究在塑相土壤条件下履带式拖拉机的行驶性能，故土壤含水量设置为30.0%～50.0%。结合前期研究测试结果[7−9]，土壤密度范围设置为1.6～2.4 g/cm3。履带式拖拉机耕作时速度一般为2.0～10.0 km/h[21]，故确定其行驶速度范围为2.0～10.0 km/h。各试验因素水平如表2所示。

表2 试验因素水平编码Table 2 Coded levels for different factors

2.2 试验指标及其计算

履带式拖拉机在塑相水田中行驶时，行驶系统产生下陷并直接影响行驶阻力，同时，履带的附着性也影响驱动力，因此，将行驶阻力、下陷深度作为履带式拖拉机性能试验指标。仿真试验过程中RecurDyn软件可以同步记录机架垂直位置参数、驱动链轮转矩和转速等信息。依据驱动轮转矩计算瞬时行驶阻力，以机架在垂直方向的位置变化及行驶系统与水田土壤表面的相对位置计算瞬时下陷深度。在仿真试验开始5 s后，即整机前进速度稳定后，选择5～10 s内记录的数据，计算行驶阻力、下陷深度的平均值。

2.3 试验方法

利用四因素五水平二次正交组合设计方法安排试验。采用RecurDyn软件设定试验因素水平，通过添加动力驱动进行仿真试验，仿真时间设置为10 s。开始时履带式拖拉机在重力作用下自由下落并与土壤接触，0～1 s保持静止，＞1～3 s开始加速至设定值，3 s 之后达到预定行驶速度，平稳运行至10 s，仿真结束。以5～10 s 期间记录的数据为基础计算试验指标。

采用Design-Expert 7.0软件对试验数据进行分析处理。以行驶阻力、下陷深度为响应值，以水田土壤黏粒含量、含水量、密度以及行驶速度为自变量，响应值与自变量的关系用二次多项式回归模型表示：

式中：Yi分别为行驶阻力（Y1）、下陷深度（Y2）试验响应值；X1、X2、X3、X4依次为土壤黏粒含量、含水量、密度以及行驶速度等自变量的编码值；β0、β1、β2、β3、β4、β12、β13、β14、β23、β24、β34、β11、β22、β33、β44为预测模型的回归系数。

3 结果与分析

3.1 试验结果与回归分析

试验方案及结果如表3 所示，相关统计分析结果如表4所示。由表4可知：在P＜0.05水平，X2、X3、X4、X1X3与行驶阻力Y1的系数显著，其余不显著，模型的P值＜0.001，决定系数（R2）为0.92，说明回归模型极其显著且具有很高的拟合精度；X1、X2、X3、X1X2、X1X4、X2X4与下陷深度Y2的系数显著，其余项不显著，模型的P值＜0.001，R2为0.89，说明回归有效。因水田土壤黏粒含量对其承载特性影响明显[9]，进而影响行驶阻力，且水田土壤黏粒含量X1对应的P值仅为0.059 9，略高于显著性水平0.05，故在行驶阻力回归方程中仍保留X1。将其他不显著项删除后得到行驶阻力（Y1）和下陷深度（Y2）的响应值回归方程，如式（2）和式（3）所示。利用这2 个方程可以对履带式水田拖拉机在不同水田条件与作业速度下的行驶性能进行预测。

表3 试验方案及结果Table 3 Experimental schemes and results

根据表4中土壤黏粒含量、含水量、密度以及行驶速度的回归系数的F值，单因素对行驶阻力的影响由高到低依次为X2、X4、X3和X1，交互作用由高到低依次为X1X3、X1X4、X1X2、X2X3、X3X4、X2X4，单因素对下陷深度的影响由高到低依次为X2、X3、X1和X4，交互作用由高到低依次为X1X2、X1X4、X2X4、X3X4、X1X3、X2X3。

表4 试验统计分析结果Table 4 Results of statistical analysis for experiment

3.2 单因素对响应值的影响

采用降维方法分析单因素对响应值的影响效应，根据响应值回归方程，将其他因素设定为零水平，采用单因素效应方程描述各因素对响应值的影响，其效应曲线如图2 所示。行驶阻力随着土壤黏粒含量、含水量的增加而单调增加，随着土壤密度和行驶速度的增加而减小，而下陷深度随着土壤含水量增加而增加，随着土壤黏粒含量、密度以及行驶速度的增加呈减小趋势。

图2 单因素对响应值的影响Fig.2 Effects of single factor on the response values

3.3 交互因子对响应值的影响

以土壤黏粒含量、含水量、密度以及行驶速度中的任意2 个因素作为交互因子，履带式水田拖拉机行驶阻力、下陷深度的响应曲面及等高线图分别如图3和图4所示。

由图3A和图4A知：在土壤密度为2.0 g/cm3、行驶速度为6.0 km/h时，随着土壤黏粒含量增加、含水量降低，行驶阻力、下陷深度均下降。这主要是随着土壤黏粒增加，土壤黏聚性增强，同时，土壤含水量降低，土壤的承载能力提高[9]，使拖拉机下陷深度减少，从而降低了行驶阻力。当土壤黏粒含量编码值在－2～－1（黏粒含量20.0%～25.0%）之间、含水量编码值在－2～－1（含水量30.0%～35.0%）之间时，行驶阻力、下陷深度均存在较小值。等高线图结果表明，行驶阻力、下陷深度沿土壤含水量特征参数方向的变化速率远高于土壤黏粒含量方向，即土壤含水量对行驶阻力、下陷深度的影响大于土壤黏粒含量对行驶阻力的影响。

由图3B 和图4B 知：在土壤含水量为40.0%、行驶速度为6.0 km/h 时，履带式水田拖拉机在较低密度土壤（编码值小于0）中行驶阻力随着土壤黏粒含量增加而略有下降，较高密度土壤（编码值大于0）行驶阻力随着土壤黏粒含量增加而增加，下陷深度随土壤黏粒含量增加而略有下降。这主要是由于塑相土壤承载能力和坚实度随着其黏粒含量和密度增加均呈增加趋势[8−9]，降低了拖拉机下陷量，从而降低了行驶阻力。随着土壤密度增加，下陷深度降低，在黏粒含量较低的土壤中行驶阻力随土壤密度增加而减小，但在黏粒含量较高的土壤中行驶阻力随土壤密度增加而增加。这主要是由于黏性土壤的剪切强度随黏粒含量增加急剧增加，从而造成行驶过程中行驶部件要克服更大的土壤剪切应力[7]。土壤密度编码值在1～2（密度2.2～2.4 g/cm3）之间时，黏粒含量编码值为－2～－1（黏粒含量20.0%～25.0%）时，行驶阻力有较小值；在黏粒含量编码值为1～2（黏粒含量35.0%～40.0%）时下陷深度存在较小值。

由图3C和图4C可知，在土壤含水量为40.0%、土壤密度为2.0 g/cm3时，随着土壤黏粒含量增加，行驶阻力增加；当土壤黏粒含量编码值为－2～－1（黏粒含量20.0%～25.0%）时，随着行驶速度增加，行驶阻力和下陷深度均降低，且行驶速度编码值为1～2（土壤密度2.2～2.4 g/cm3）时行驶阻力存在较小值；当黏粒含量编码值大于0时，在不同行驶速度下行驶阻力均较大，下陷深度随行驶速度增加而略有增加。中低速度行驶（编码值小于0）时，土壤黏粒含量对行驶阻力影响较小，下陷深度随土壤黏粒含量增加而减小；高速度行驶（编码值大于1）时，行驶阻力和下陷深度均随土壤黏粒含量增加而增加。

由图3D 和图4D 可知：在土壤黏粒含量为30.0%、行驶速度为6.0 km/h 时，随着土壤含水量增加，拖拉机行驶阻力、下陷深度均增加，而随着土壤密度增加，行驶阻力、下陷深度均降低。主要原因是土壤种类和含水量对其力学性质产生了影响[10]，随着土壤含水量增加、密度降低，其坚实度均急剧下降[8]，造成拖拉机下陷深度增加，从而行驶阻力增大。当土壤含水量编码值在－2～－1（含水量30.0%～35.0%）之间、密度编码值在－2～2（密度1.6～2.4 g/cm3）之间时，行驶阻力均存在较小值；土壤密度编码值在1～2（密度2.2～2.4 g/cm3）之间时，下陷深度存在较小值。等高线图结果表明，行驶阻力、下陷深度沿土壤含水量特征参数方向的递增速度大于密度参数方向。

由图3E 和图4E 可知，当土壤黏粒含量为30.0%、密度为2.0 g/cm3时，随着土壤含水量增加，行驶阻力、下陷深度均增加；随着行驶速度增加，在较低含水量（小于40.0%）的土壤中行驶阻力、下陷深度均减小，在较高含水量（大于40.0%）的土壤中行驶阻力、下陷深度均较高。当土壤含水量编码值在－2～－1（含水量30.0%～35.0%）之间、行驶速度编码值在1～2（行驶速度8.0～10.0 km/h）之间时，行驶阻力存在较小值。

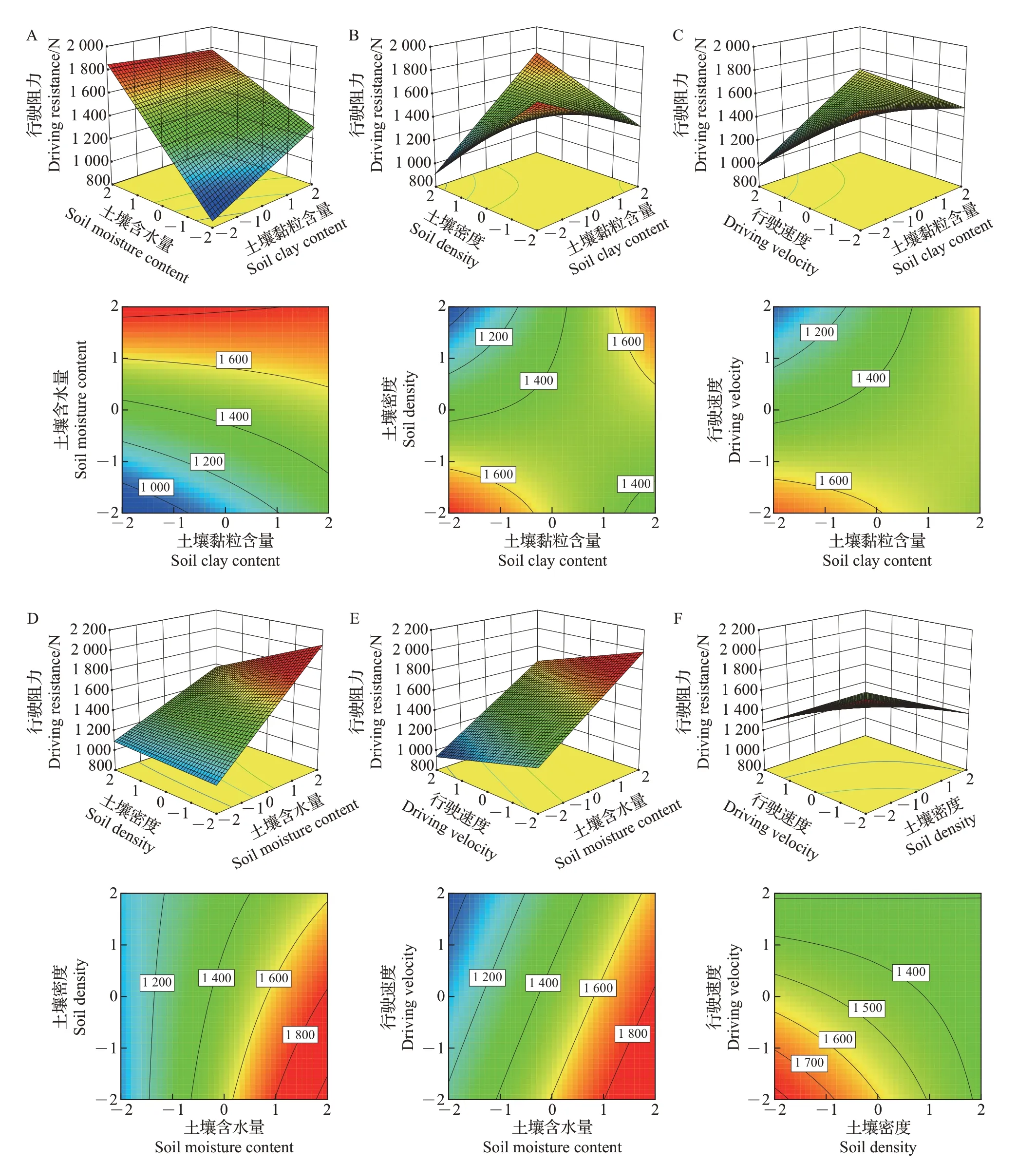
图3 交互因子对行驶阻力的影响Fig.3 Interactive effects of two factors on the driving resistance

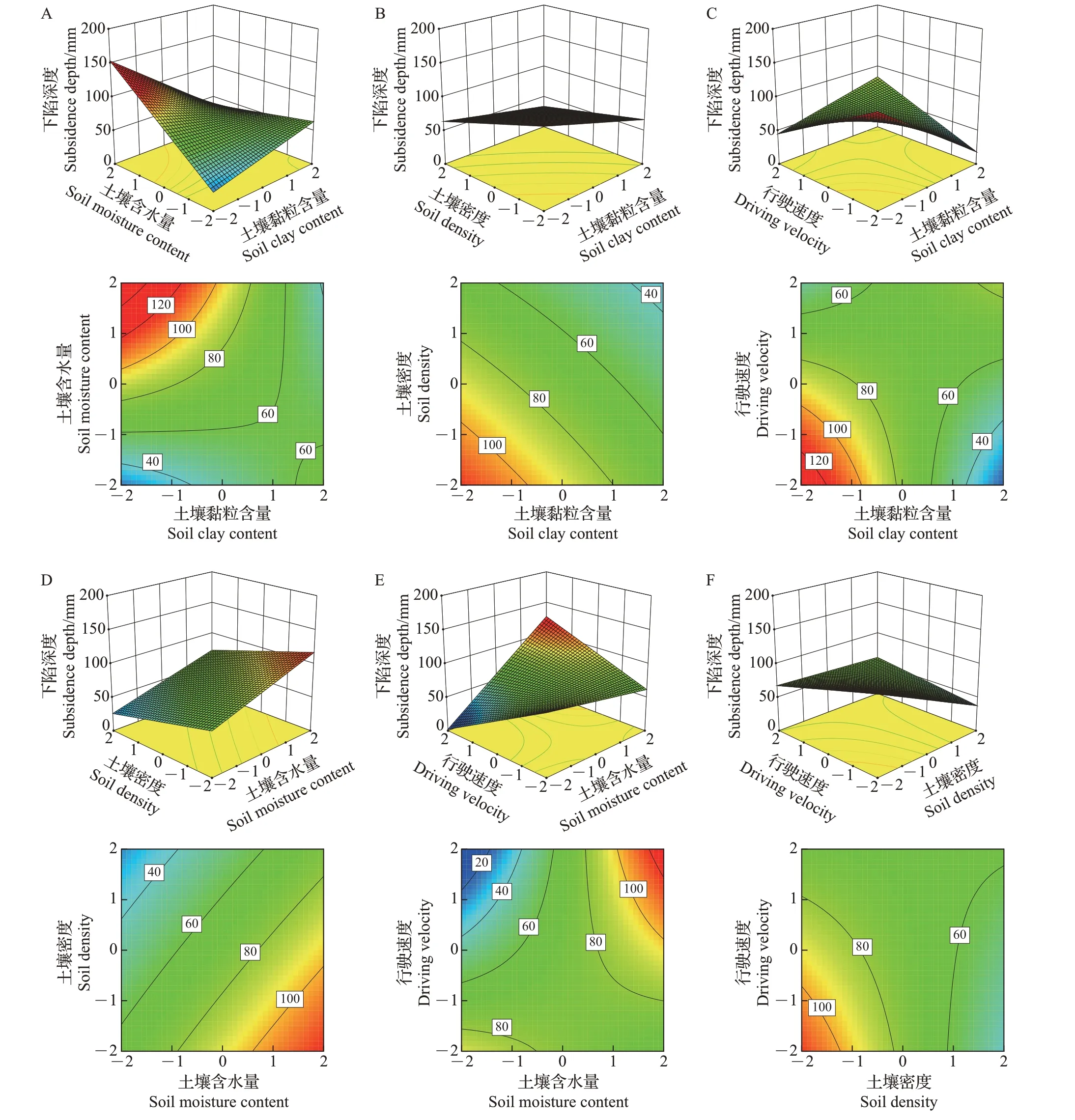
图4 交互因子对下陷深度的影响Fig.4 Interactive effects of two factors on the subsidence depth

由图3F 和图4F 知，在土壤黏粒含量为30.0%、含水量为40.0%时，随着土壤密度、行驶速度增加，行驶阻力、下陷深度均呈下降趋势。这主要是由于随着密度增加土壤坚实度提高[8]，履带式拖拉机行驶部件承载能力增强。当密度编码值在1～2、行驶速度编码值在1～2之间时，行驶阻力存在较小值。

综合图3～4和表4可知，土壤含水量是影响行驶阻力的主要因素。这主要是由于随着含水量增加，塑相土壤的内聚力、摩擦模量、硬度等均明显下降[7−9]，土壤承载性能变差，导致行驶阻力增加。

3.4 参数优化

为了确定履带式水田拖拉机田间作业的较佳土壤条件和作业速度，需要综合考虑各因素对预测指标的影响。设置行驶阻力、下陷深度的权重相同，进行多目标参数优化。以行驶阻力、下陷深度极小化为目标，利用Design-Expert 7.0 软件对回归方程模型作多目标优化求解。

式中，f1和f2为各响应方程的最小值。

优化结果为：X1=0.30，X2=－1.82，X3=－1.35，X4=1.62，即最优参数组合为土壤黏粒含量31.5%、土壤含水量32.6%、土壤密度1.72 g/cm3、行驶速度8.6 km/h，此时的行驶阻力最优解为1 295.22 N、下陷深度为51.31 mm。在实测的典型水田粉壤土（黏粒20.2%、粉粒60.8%）、粉黏壤土（黏粒29.8%、粉粒61.6%）、黏壤土（黏粒35.3%、粉粒44.4%）中，将土壤黏粒含量值、密度值导入目标函数，进行最优参数求解，获得履带式水田拖拉机在以上水田土壤中工作的较佳参数组合，结果如表5所示。可见，通过模型能够优化获得水田履带式拖拉机在不同质地水田土壤中阻力最小时的作业速度（行驶速度）和土壤含水量。

表5 不同水田土壤类型优化参数组合Table 5 Optimal parameter combinations for different paddy soil types

4 结论

1）利用RecurDyn 软件建立了履带式水田拖拉机与塑相水田土壤间相互作用模型，获得了水田土壤黏粒含量、含水量、密度以及行驶速度对履带式水田拖拉机行驶阻力和下陷深度的影响关系。

2）土壤黏粒含量、含水量、密度以及行驶速度对履带式水田拖拉机行驶阻力有明显影响。行驶阻力随着土壤黏粒含量、含水量的增加而增加，随着土壤密度和行驶速度的增加而减小；各因素交互作用对行驶阻力的影响中，仅土壤密度与黏粒含量的交互作用影响显著，其他交互作用的影响均不明显，各因素影响行驶阻力的主次关系依次为土壤含水量、行驶速度、土壤密度以及土壤密度与黏粒含量的交互作用。

3）土壤黏粒含量、含水量、密度对履带式水田拖拉机下陷深度均有显著影响，行驶速度的影响不明显；黏粒含量与含水量交互作用、黏粒含量与行驶速度交互作用、含水量与行驶速度交互作用对下陷深度有明显影响，其他交互作用的影响不明显，影响下陷深度的各因素主次关系依次为土壤含水量、密度、黏粒含量以及黏粒含量与含水量交互作用、黏粒含量与行驶速度交互作用、含水量与行驶速度交互作用。

4）建立了履带式水田拖拉机行驶阻力、下陷深度与水田土壤物理参数、行驶速度间的优化模型，对任意已知土壤黏粒含量、密度等参数的不同类型水田，能够优化获得行驶阻力最小值时的土壤含水量、拖拉机行驶速度，对降低履带式水田拖拉机在水田作业中的能耗具有重要意义。