由欧拉角确定一次回转轴的简单解法

张 媛 王士敏 王 琪

(北京航空航天大学，北京 100083)

欧拉角以及一次回转轴，不仅在教学上是理解定点运动的基础，而且在应用方面，如进行航天器、机器人、机械手等刚性部件的姿态描述、大角度姿态机动的轨迹规划[1]等，也起着重要作用。

首先，欧拉角便于刚体姿态的描述，欧拉角是三个独立的广义坐标，当章动角不为零时，刚体姿态与欧拉角一一对应，两组欧拉角之差反映了刚体的有限位移。当章动角为零时，其运动退化为定轴转动，转轴的位置以及刚体转过的角度仍然是确定的，转动角度可以视为进动角与自转角之和，一旦根据其他条件给出自转角的值，刚体姿态又可以与欧拉角一一对应。而定点运动刚体有限位移的一次回转轴，对于有限位移，给出姿态机动的最小路径，对于微小位移，则给出了瞬轴或角速度的方位。

结合定点运动的教学内容，以及一次回转轴的应用背景，这里介绍了利用欧拉角以及随体坐标系到固定坐标系之间的变换矩阵，构造出任意姿态之间有限位移一次回转轴位置以及计算转角的方法。该方法基于定轴转动时刚体上点的位移特性得出，与求解矩阵特征向量的方法相比较，几何意义更为直观，计算简单。在应用上，既可以像四元数法一样用于刚体姿态接续机动的规划，又可以作为辅助参数，消除章动角为零时欧拉角的奇异性，使得表述定点运动刚体的运动学、动力学方程所用的广义坐标一致，几何意义明确。

1 方法

1.1 方法的几何解释

问题：如图1 所示，设刚体的姿态A和姿态B分别对应于欧拉角(ψA,θA,φA) 和(ψB,θB,φB)，求解刚体从姿态A到姿态B的有限位移的一次回转轴与转角。

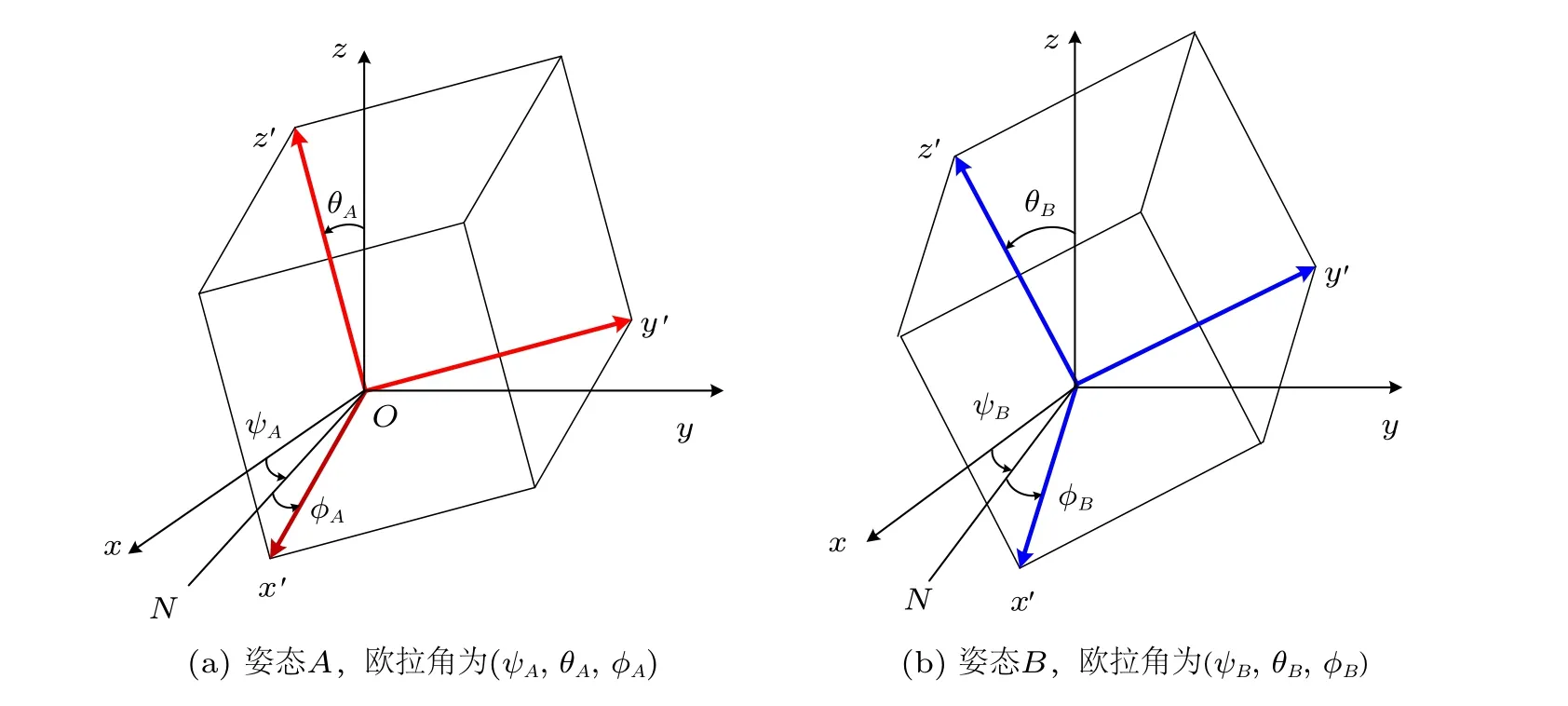
图1 刚体的姿态A 和姿态B 位置

刚体由姿态A机动至姿态B时，欧拉角由(ψA,θA,φA)变化至(ψB,θB,φB)，相应地，随体坐标轴单位向量由i′A，j′A，k′A变化至i′B，j′B，k′B，如图2 所示。设单位向量端点的位移分别为Δi′，Δj′，Δk′，再假设一次回转轴的单位方向向量为l。

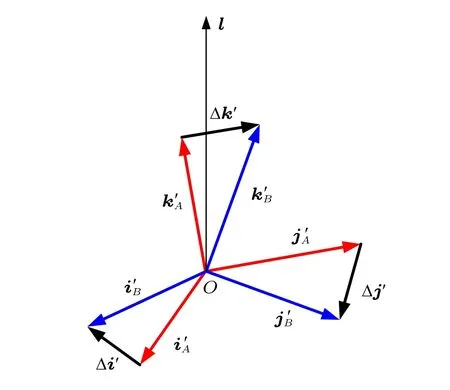
图2 随体坐标系单位矢量末端的有限位移

基于欧拉-达朗贝尔定理，定点运动刚体的有限位移可通过绕一固定轴作一次转动实现，那么在该定轴转动中，利用刚体上任一点的位移矢量与该转轴垂直，便可求出一次回转轴的方向向量。因此在上述三个位移中任选两个，比如Δi′和Δj′，即可构造出一次回转轴的位置，如果上述两个位移中有一个为零，那么，该单位向量便是一次回转轴的位置，如果两个均不为零，由于它们均与l正交，则一次回转轴的方向向量，可通过计算两个位移的叉积得到

其中a为待定系数。

在一次回转轴的位置确定后，利用刚体绕l定轴转动时，向量i′的位置变化，以及其末端到l的距离不变，便可以求出相应的一次回转角。如图3 所示，在姿态A时，过i′A的端点A作l的垂线交l于点C，刚体由姿态A机动至姿态B时，向量i′绕l作定轴转动至i′B，AC转过角度β后到达BC位置。

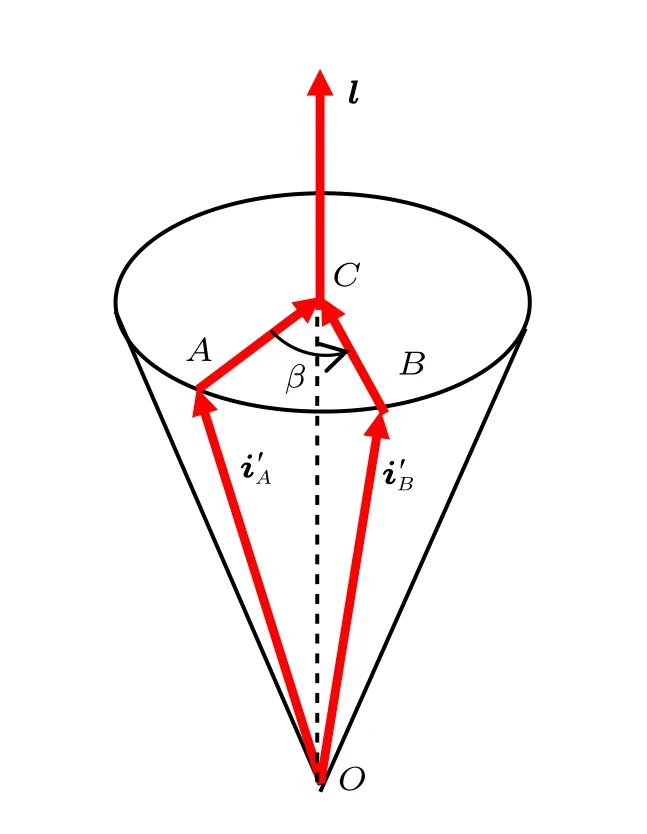
图3 随体坐标轴x′ 方向的单位向量绕一次回转轴转动

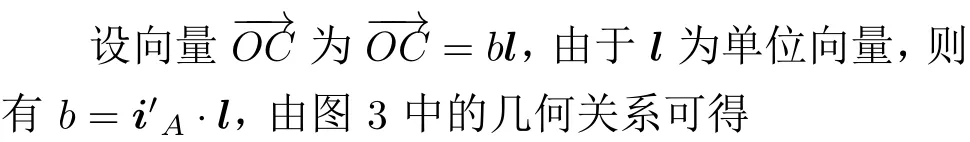
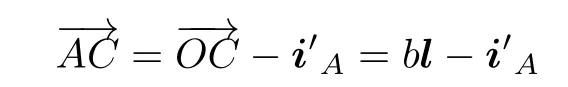
由此得到一次回转角β。

1.2 由欧拉角表示的一次回转轴与转角

刚体上一点M在随体坐标系下坐标为(x′,y′,z′)，在固定坐标系下坐标为(x,y,z)，存在以下关系式[3]

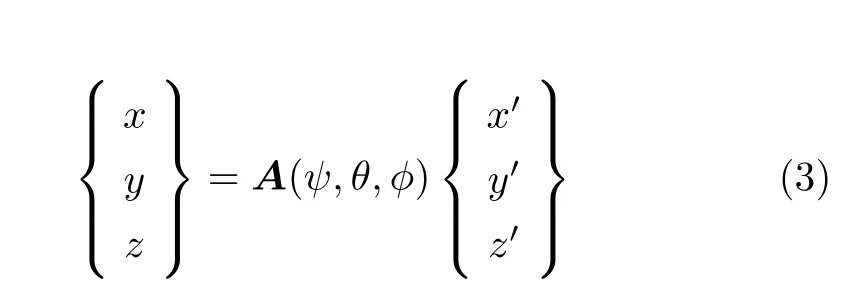
(ψ,θ,φ)为刚体当前姿态对应的欧拉角，其中坐标变换矩阵为

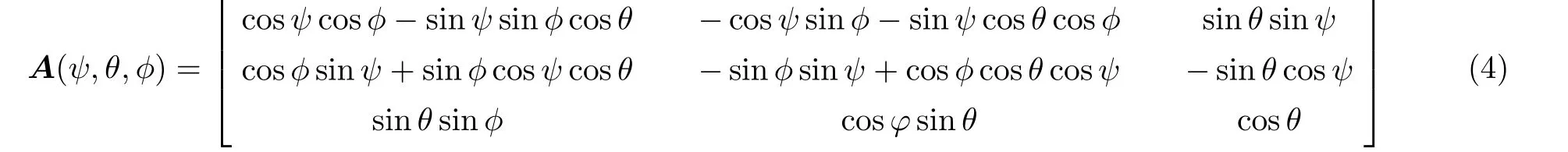
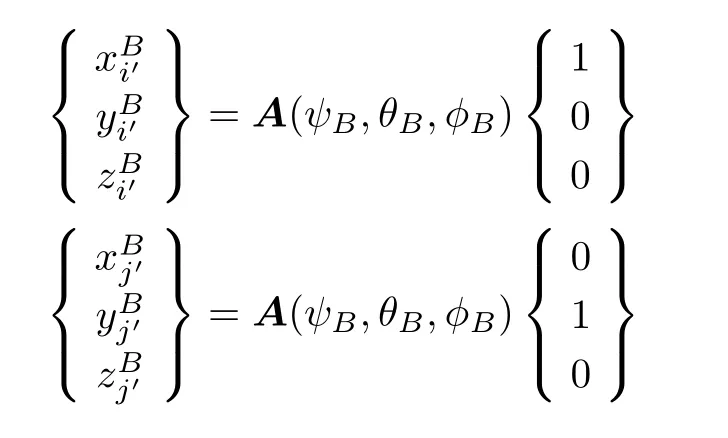
进一步有

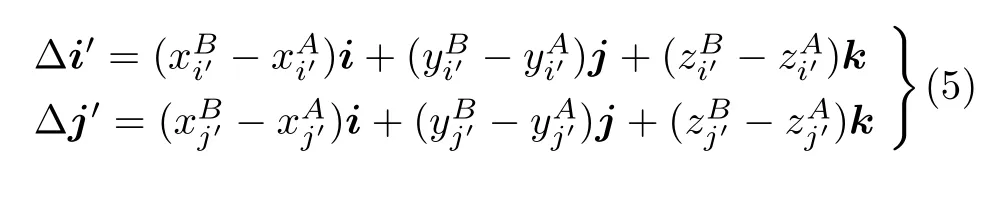
将式(5) 代入式(1)，可得一次回转轴的单位向量为

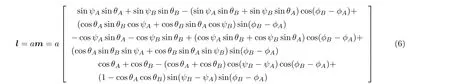
其中m=Δi′×Δj′，a=1/|m|。

为了便于验证，假设姿态A为初始姿态，即ψA=θA=φA= 0，将这三个欧拉角代入式(6)后可得

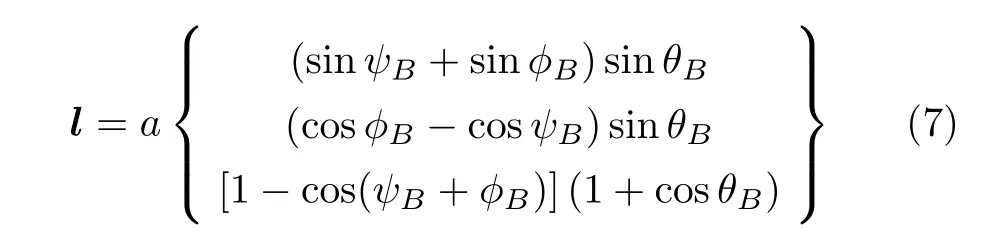
将式(6) 再代入式(2)，可得两个位置之间的一次回转角β，由于用欧拉角表示的转角计算公式过于冗长，这里不列出其具体表达式。

2 算例分析

为了便于进行较为直观的验证，这里给出一个简单的算例，设刚体由随体坐标与固定坐标相重合的姿态A出发，如图4(a) 所示，作一系列姿态机动，先绕Oz(OC) 进动π/2 到图4(b) 所示位置，再绕Oy(OA) 章动π/2 到图4(c) 所示位置，最后绕Ox(OC) 自转π/2 到图4(d) 所示的位置。刚体从姿态A到姿态D对应的欧拉角依次为(0,0,0)，(π/2,0,0)，(π/2,π/2,0)，(π/2,π/2,π/2)，其中，括弧中三个欧拉角依次为进动角、章动角和自转角。

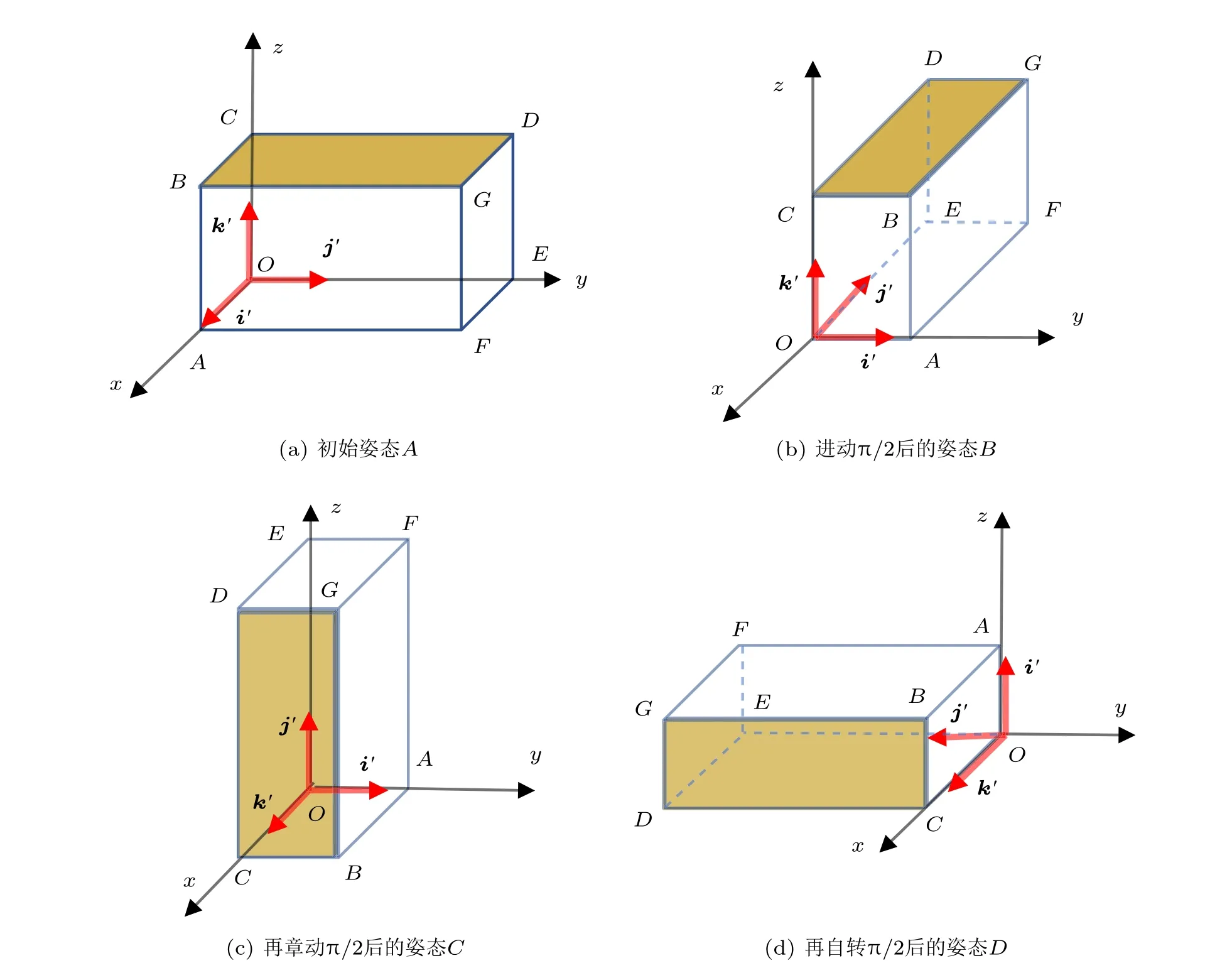
图4 刚体从初始姿态到姿态D 的机动过程

例1 计算姿态A到姿态D的一次回转轴，如图5 所示。

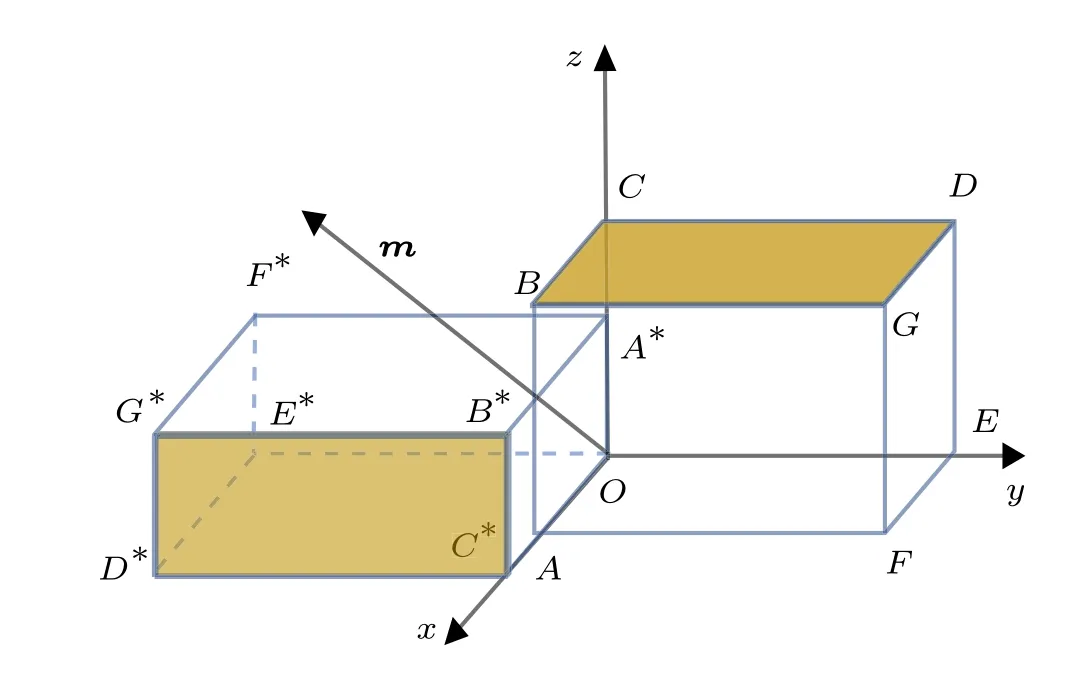
图5 姿态A 到姿态D 一次回转轴

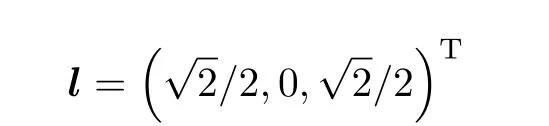
首先根据式(7)，计算长方体从姿态A到姿态D的一次回转轴的单位方向向量可得将l代入式(2)，可得回转角β= π；参照图5 可看出，一次回转轴的方向向量为m=i+k=(1,0,1)T，回转角为β=π。

下面利用求解变换矩阵特征向量的方式进行验算。变换矩阵A(ψ,θ,φ) 为正交阵，由线性代数理论可知该矩阵存在特征值为1 的特征向量，满足

利用特征向量方法，仅可以求出有限位移的一次回转轴，若求解相应的转角，还需进一步的计算，这里可由式(2) 给出。下面验证任意姿态之间有限位移的一次回转轴及转角公式。

例2 计算姿态B到姿态D的一次回转轴，如图6 所示。

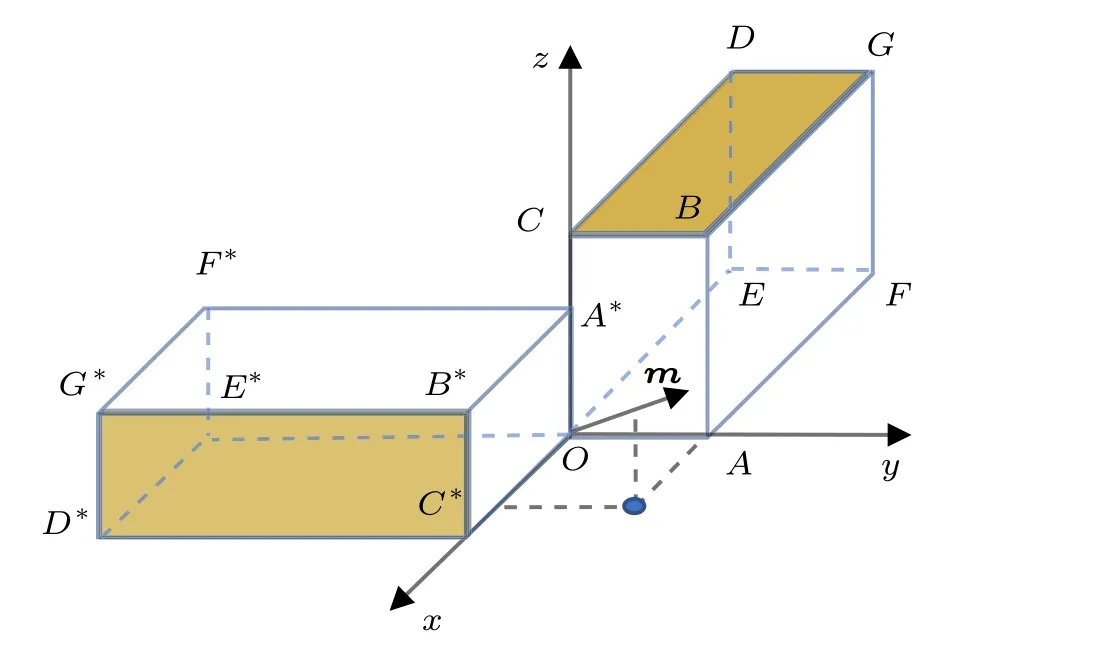
图6 姿态B 到姿态D 的一次回转轴

首先将姿态B和姿态D的欧拉角代入式(6)，可得一次回转轴的单位方向向量

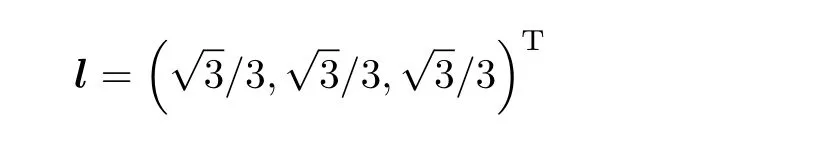
将l代入式(2) 可得回转角β=2π/3；如图6 所示，一次回转轴的方向向量m=i+j+k=(1,1,1)T。

再利用求解变换矩阵特征向量的方法进行验算，设刚体上一点M的随体坐标为(x′,y′,z′)，令其在姿态B和姿态D下的绝对坐标分别为(xB,yB,zB)和(xD,yD,zD)，通过式(3) 可得(xB,yB,zB)T为从姿态B机动至姿态D的一次回转轴的方向向量。将姿态B和姿态D对应的欧拉角代入式(9)，经计算可得

示例表明，这里给出的任意姿态之间有限位移的一次回转轴与通过变换矩阵求特征向量方法一致，比较两种方法的求解过程，发现计算矩阵特征向量的方法涉及到对矩阵进行求逆及求解特征向量等运算，而利用本文给出的方法所推导的公式只有简单的代数运算，计算量显著减小。

3 结论

本文利用欧拉-达朗贝尔定理所证明的有限位移一次回转轴的存在性，通过欧拉角以及随体坐标到固定坐标的变换矩阵，构造出了任意两个姿态之间有限位移的一次回转轴，避免了先求解任意姿态之间的变换矩阵再求解其特征向量的复杂运算过程。该构造方法几何意义明确，涉及到的基本概念简单，便于理解。在应用方面，可以由具有独立性的欧拉角和欧拉角速度描述刚体的运动学以及动力学方程，由欧拉角给定的一次回转轴、转角作为辅助参变量，消除章动角为零时的奇异性问题，相比于其他参数表述运动学方程更为直观。