柔性车间的多工艺路线与布局联合优化
2022-03-11汤洪涛梁佳炯陈青丰
汤洪涛,梁佳炯,陈青丰
(浙江工业大学 机械工程学院,浙江 杭州 310023)
0 引言
随着制造技术的不断发展,传统工艺规划开始向柔性工艺规划转变[1]。在柔性工艺规划中,每一种产品可以选择多条工艺路线,工艺路线主要通过3种柔性方式产生:①工艺流程柔性,即产品的部分加工工艺本身可选择替换,例如某道工序既可以通过拉伸实现,也可以通过挤压实现;②工艺顺序柔性,即部分加工工艺的先后顺序可以交换;③加工机器柔性,即部分工序使用的机器可以选择替换。柔性工艺使得对柔性车间进行布局优化设计时需要将工艺路线同时作为优化对象,从而产生多工艺路线与车间布局联合优化的概念和需求。
国内外学者针对各种车间布局类型进行了大量研究[2]。在各类布局问题建模上,通常将问题局限于将若干设施分配到若干区域,即二次分配问题(Quadratic Assignment Problem, QAP),并将其他约束作为独立约束条件[3],仅有少量研究将设施布置以外的约束作为非独立变量(即变量之间相互影响)纳入问题模型[4]。
多工艺路线与车间布局联合优化将工艺路线作为非独立变量,而产品的不定需求会影响多工艺路线规划,因此需要在动态环境下进行联合优化。针对动态环境下的车间布局研究主要有动态设施规划问题(Dynamic Facility Layout Problem ,DFLP)和鲁棒布局规划两种技术路线。前者通过时间分段,将动态环境转化为一系列不同时间段上的静态环境[5],从而将DFLP转换为静态设施规划问题[6](Static Facility Layout Problem ,SFLP),同时附加不同时间段重新布局的转换成本[7];后者不追求某个时间段布局的目标函数最优,而是追求整个时间段的总体布局目标函数最优[8],以减少重新布局对生产的影响。相比之下,鲁棒布局规划更适用于设施位置变动比较困难的工厂。
针对鲁棒布局规划,MOSLEMIPOUR等[9]提出基于QAP的制造系统随机动态环境下鲁棒机械布局设计的数学模型,然而其中等设备面积的假设不切实际;周娜等[10]、马淑梅等[11]、ZHA等[12]针对产品需求不确定性引起的动态设施布局问题,各自提出面向不等面积设备的鲁棒布局设计方法。在实际生产中,产品需求变化会对工艺路线选择产生影响,但目前的鲁棒布局研究较少将多工艺路线纳入优化模型,李聪波等[13]、DEEP等[14]各自提出基于所选择的最优零件工艺路线并考虑产品需求的鲁棒车间布局模型。上述研究将多工艺路线规划作为影响车间布局的参数因素体现在模型中,忽略了多工艺路线与车间布局之间的相互影响,为了对两者进行整体优化,需要将多工艺路线作为变量来设计模型。因此,基于鲁棒布局方法研究,本文提出面向不等面积设备的多工艺路线与车间布局联合优化模型。
车间布局问题的求解方法可以归为精确方法、启发式、元启发式和混合方法4类[15]。设施布局问题属于NP难问题,各类元启发方法和混合方法是目前求解车间布局问题常用的方法。传统的设施规划问题只需求解一个变量,而联合优化问题中存在多个需要求解的非独立变量。以往的联合优化问题研究一般有两种求解方法:①将非独立变量进行整合编码[16],即在算法求解时将多个变量看作单一变量进行寻优求解;②将联合优化问题拆解成多个单独优化问题,借助元启发方法分阶段对联合优化问题进行求解。例如文笑雨等[17]提出工艺路线规划与车间调度集成优化方法;李言等[18]提出以加工时间、成本和设备负载为优化目标的工艺规划与调度集成优化模型。然而,两种优化求解方法均忽略了变量之间的影响,理论上缩小了解空间。因此,本文针对联合优化问题提出多决策变量智能优化算法,该算法以整体函数优化为导向,单独、同时对各变量的解进行优化迭代,迭代过程中不同变量的解之间相互没有影响,防止出现各子问题先后迭代至最优,总优化目标却不为最优的情况,同时各决策变量采用不同的优化迭代方法,保证了整体解的寻优效率和多样性,并对多工艺路线与车间布局联合优化模型进行了优化求解和验证。
1 多工艺路线与车间布局联合优化模型
1.1 问题描述
问题源自浙江某锅具制造龙头企业的柔性车间布局设计项目。以该企业的A车间为例,车间生产的产品共有11种,涉及加工设备15种,涉及工艺19道。柔性车间的生产柔性主要体现在工艺流程柔性、工艺顺序柔性和加工机器柔性3方面。不同设备在不同时刻可以用于加工多个工件的多道工序,工件的加工设备也具有可选择性。这类柔性车间一般以降低总体物流成本为目标进行两阶段布局与工艺规划[19]:①基于工艺约束构建模型,求解得到各工件的工艺路线;②以第一阶段求解得到的工艺路线为基础进行车间布局建模,再求解得到方案。两阶段优化设计方法将复杂的联合优化问题拆解为易于求解的两个子问题进行逐步求解,然而求解过程中忽略了子问题之间的相互影响,以一阶段最优工艺路线为参数得到的车间布局方案的总体物流成本并不一定是最低的[20]。多工艺路线与车间布局联合优化模型以总体物流成本最低为优化目标,同时求解多工艺路线与车间布局,避免了先后求解上述两个子问题所产生的问题。
1.2 模型变量
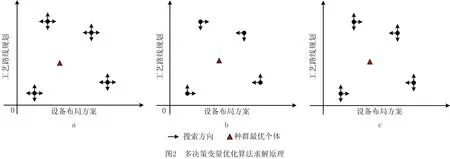
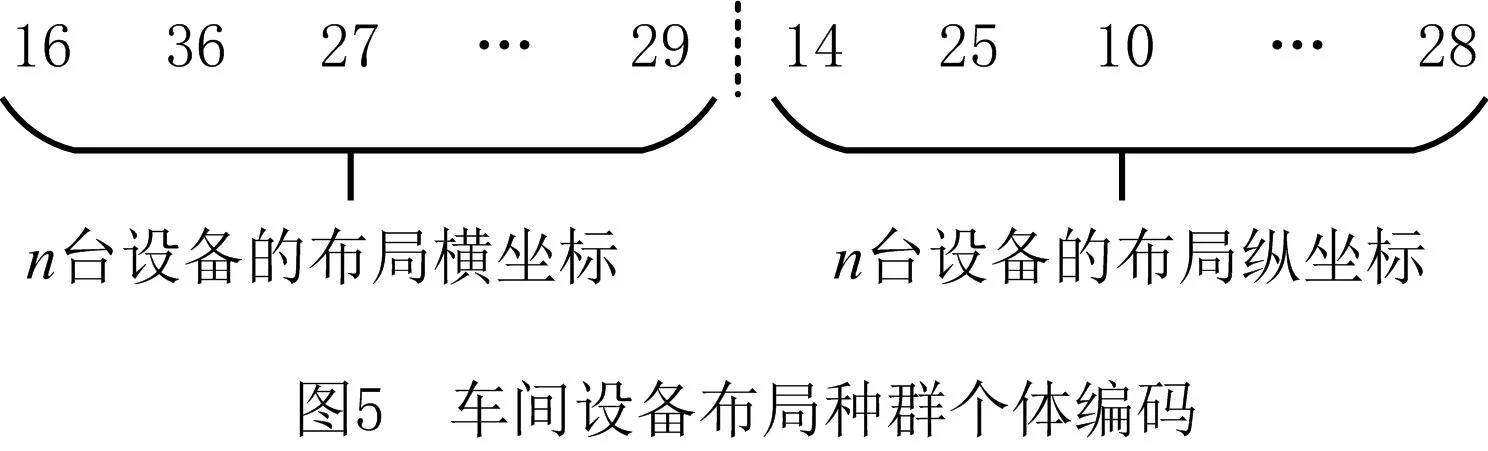
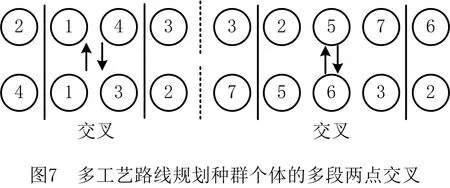
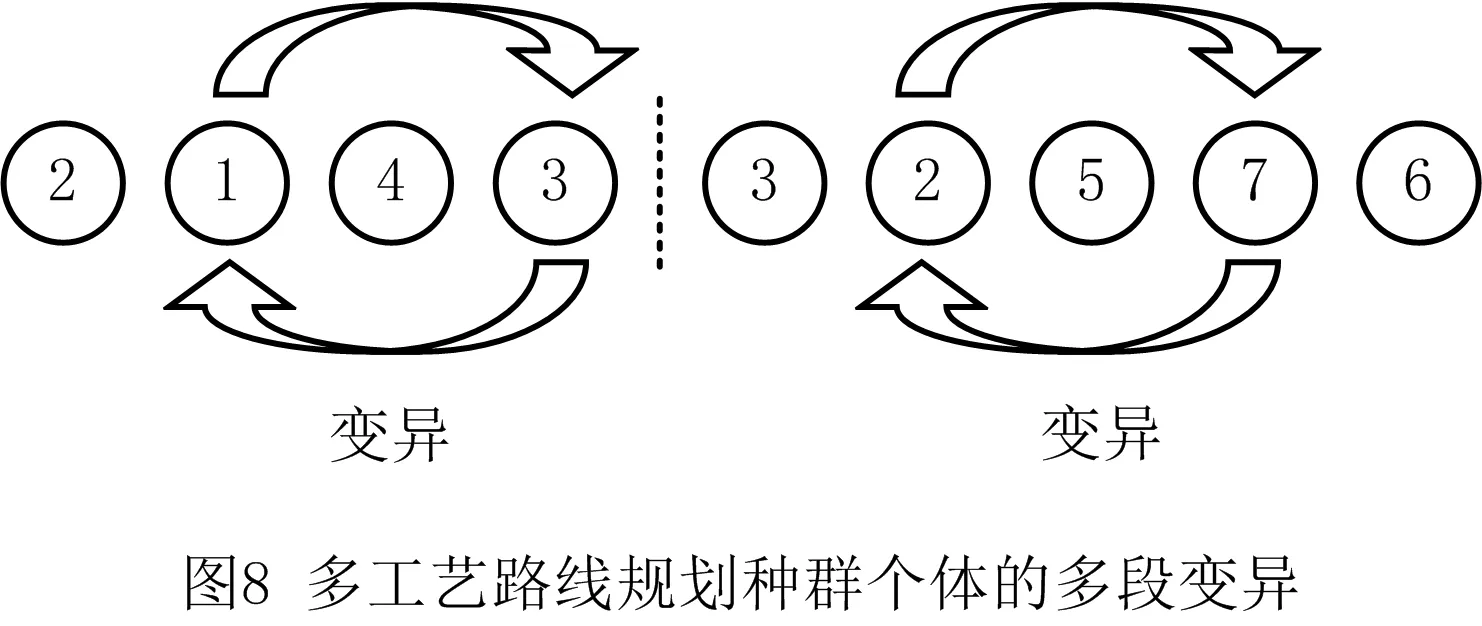
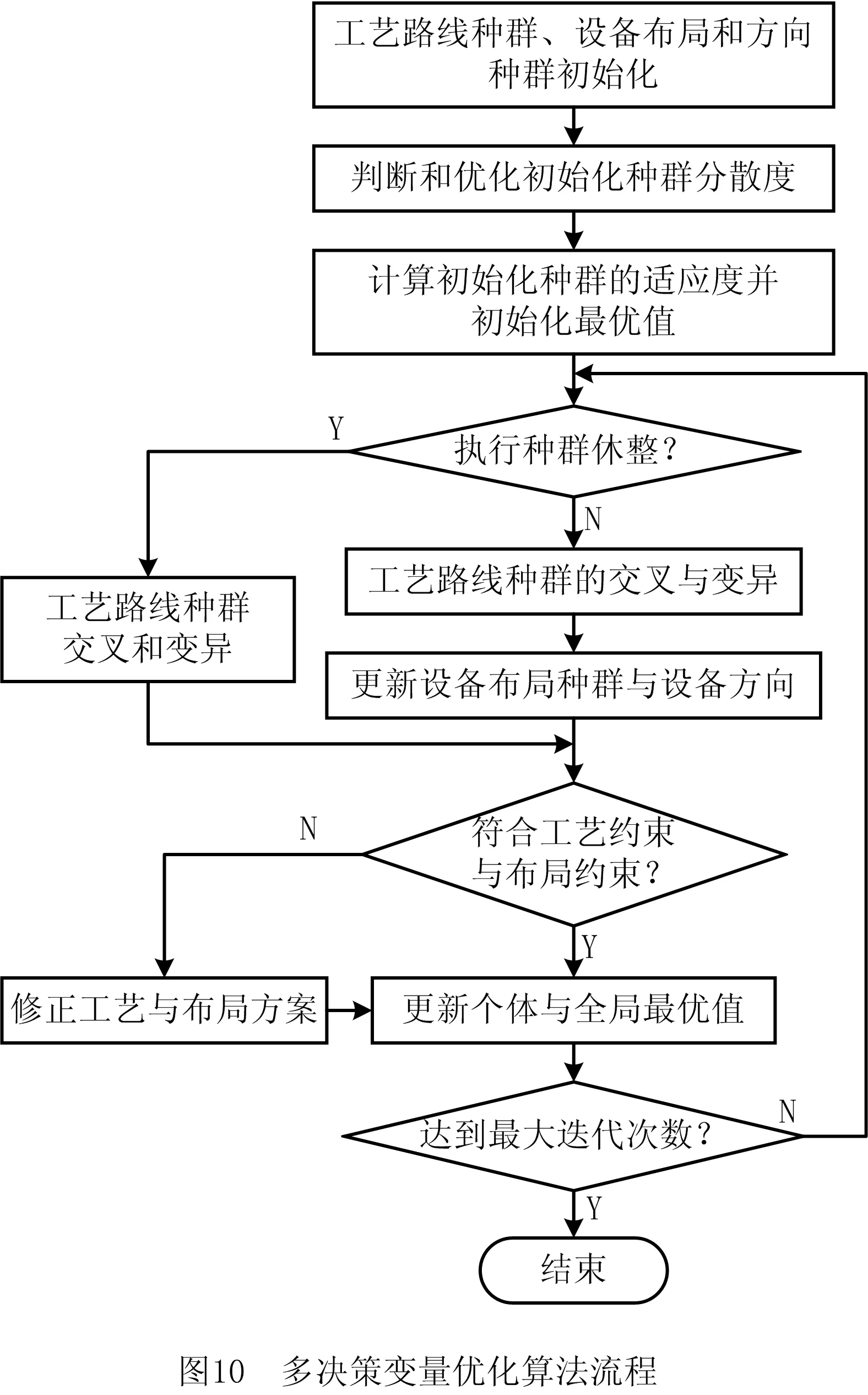
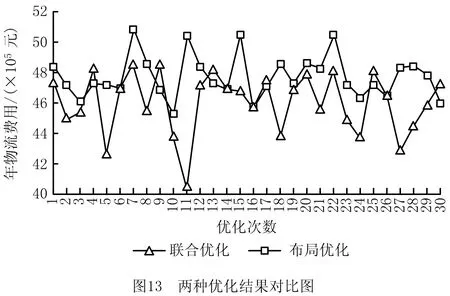
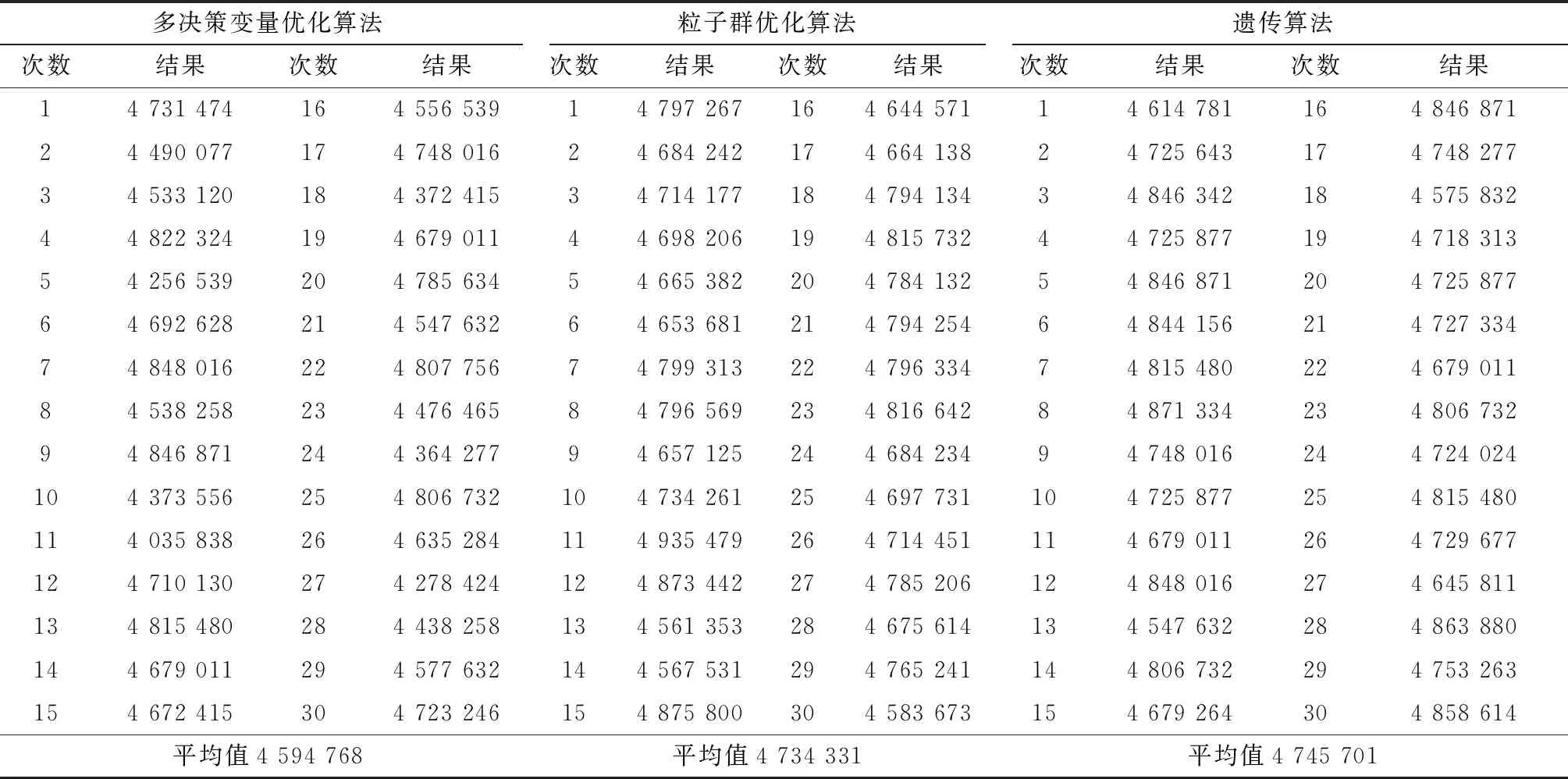
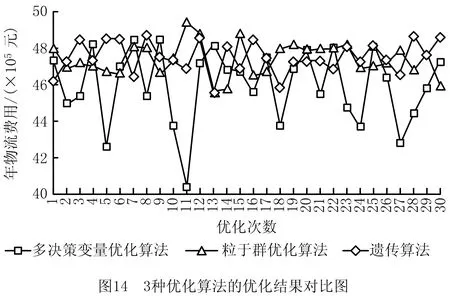
记m为车间的产品种类,n为车间工艺路线中涉及的设备数量(包括加工设备和仓库),t为车间加工设备的数量(由于包含关系,有t 定义模型中的各个变量参数,如表1所示。 表1 模型变量参数及其含义 1.2.1 工艺路线 记n阶0-1矩阵Pn×n,i为车间第i类产品的工艺路线,i=1,2,3,…,m。例如,车间共有5个设备,其第1类产品的工艺路线为2-1-4-3,则P5×5,1矩阵如图1a所示,图中每一元素的的行为上一工序的设备编号,列为下一工序的设备编号。当某种产品工艺路线中不同工序使用同一台设备,如该类产品的工艺路线为2-1-4-1-3时,工艺路线的矩阵如图1b所示;当一种产品连续出入同一台设备,如该类产品的工艺路线为2-1-1-4-3时,矩阵如图1c所示,因为连续进入同一台设备进行加工并不产生物流成本,所以该情况下的工艺路线矩阵和图1a相同;当相同的配送段多次出现在一条产品工艺路线中,如该类产品工艺路线为2-1-4-2-1-3时,矩阵如图1d所示。 1.2.2 设备间距 d12=|x1-x2|+|y1-y2|。 (1) 1.2.3 设备换模 在实际生产中,随着产品种类和数量的增加,加工设备的换模物流成本也会增加。记列向量d1×t为车间各加工设备与模具库的距离。设车间模具库s出入口坐标为(xs,ys),则t维模具库与各设备间距的列向量d1×t=(d1s,d2s,…,dts)T,其中设备与模具库距离为 dis=|xi-xs|+|yi-ys|,i=1,2,…,t。 (2) 1.3.1 工艺约束参数 记ki,j为工艺j在第i类产品工艺路线中的序号,i=1,2,3,…,m,j=1,2,3,…,p。假设车间第1类产品的工艺路线为2-1-4-3,则其中2号工艺的序号k1,2=1,4号工艺的序号k1,4=3。 1.3.2 工艺的加工设备约束参数 记pi,j为工艺j在第i类产品工艺路线中选择的设备,i=1,2,3,…,m,j=1,2,3,…,p。假设在车间第1类产品的工艺路线中,2号工艺的设备选择3号,则p1,2=3。 (3) ki,j (4) pi,j∈Ωj,i=1,2,…,m,j=1,2,…,p; (5) (6) (7) xe=E,ye=E′,e∈B,E,E′∈R′。 (8) 其中:式(4)为工艺约束,表示在第i类产品工艺路线中,工艺j的序号小于工艺r的序号,即在第i类产品生产过程中,工艺j必须先于工艺r进行;式(5)为工艺设备选择约束,表示在第i类产品工艺路线中,工艺j选择的设备必须属于其可选设备的集合Ωj;式(6)为设备区域间距约束,表示车间布局中各设备区域之间横坐标之差的绝对值必须大于设备e与设备q的区域长度之和的1/2,或者纵坐标之差的绝对值大于宽度之和的1/2,即各设备区域不能有重合的情况;式(7)为设备区域边界约束,即设备e区域的横坐标必须大于设备e区域长度的1/2且小于车间长度与设备e区域长度的1/2之差,同时设备e区域的纵坐标必须大于设备e区域宽度的1/2且小于车间宽度与设备e区域宽度的1/2之差,即各设备区域不能超出车间边界;式(8)为特殊固定约束,表示由于特殊需要,设备e必须布置在坐标为(E,E′)的地方,如仓库和一些需要通风的设备。 目前针对多决策变量模型的算法求解,一般是将各个变量整合编码后利用统一的优化迭代思路求解。然而,智能优化算法的本质是搜索算法[21],将多种变量整合为一个变量进行寻优会在一定程度上降低整体解的搜索效率和多样性。多决策变量优化算法以种群分散度和种群休整策略为基础,通过在解的不同维度设计不同特点的优化算法对多决策变量模型进行优化求解。 全局搜索和局部寻优是智能优化算法的两大特点,算法特点不同决定了解的搜索方向不同。如果在解的两个维度都采用全局搜索,虽然能够保证解的多样性,但是牺牲了寻优效率,如图2a所示;如果两个维度都采用局部寻优,则会丧失大量解的可能性并陷入局部最优,如图2b所示;如果两个维度采用不同特点的算法,则能在理论上解决上述难题,即在初始种群个体足够分散的前提下兼顾全局搜索与局部寻优之间的协同问题,如图2c所示。 各维度算法的主要特点体现在解的产生(搜索)规则方面。智能优化算法设计主要是解的产生方式和选择规则[22],但在上述多决策变量优化算法的求解思路中,需要保留每次优化迭代中任何维度的任何解,若缺失某次迭代的解,则将减小整体解空间,甚至导致优化迭代无法进行,因此主要设计解的选择规则的算法不适用于多决策变量优化算法。 智能优化算法大致可以分为模拟退火算法、禁忌搜索算法、神经网络算法、进化类算法和群智能算法5类[23]。其中,模拟退火算法的主要特点为以小概率接受劣解的方式来体现算法的全局搜索能力,被摒弃的劣解会减小整体解的多样性,因此并不适合作为多决策变量优化算法中某个变量维度的寻优算法;禁忌搜索算法通过设置禁忌表的方式避免产生重复解,从而提高寻优效率,但在某维度解的搜索过程中使用禁忌搜索算法同样会缺失整体解,也可能丧失最优解,因此从整体角度来看,该算法也不适合作为多决策变量优化算法中某个变量维度的寻优算法;神经网络算法本身需要大量数据支撑,而且“黑匣子”无法探究其逻辑性问题,因此不适合解决规划类问题;虽然进化类算法中也有最优解的选择,但其主要通过设计交叉、变异等算子对解进行不断搜索与迭代,因此可以用于整体设计,本文选择运用最广的遗传算法;群智能算法主要通过模拟动物群体的行为对解进行搜索,个体之间信息的互联互通使得群智能算法在迭代中一直受已知最优解的影响而不需要主动对解进行选择,因此群智能算法是不剔除劣解且具有突出局部寻优特点的算法,符合本节提出的多决策变量优化算法的思路。群智能算法中粒子群优化算法和蚁群算法的运用最广,因为粒子群优化算法相对于蚁群算法的收敛速度更快,对解空间的探索能力更强,所以选择粒子群优化算法。 上一节提到只有在初始种群足够分散的情况下,多决策变量优化算法才能在求解过程中既保证局部寻优能力又不丧失解的可能性,因此需要对初始种群的分散度进行数学定义并提出优化方法。二维解空间中点的集合即为解种群,点的分散程度即为解种群的分散度,在经过不断迭代之后,解种群将越来越密集于一点(解种群覆盖范围内的最优解),即分散度越来越小,因此初始解种群的分散度越大,迭代后的最优解越好。以联合优化为例,设解空间的x轴对应车间设备布局方案,y轴对应工艺路线方案,则解r=(x1,x2,…,xm,y1,y2,…,yn)在二维解空间中的坐标为(X,Y): X=α1x1+α2x2+…+αmxm- (9) Y=β1y1+β2y2+…+βnyn- (10) Li≤xi≤Ui,i=1,2,3,…,m; (11) lj≤yj≤uj,j=1,2,3,…,n。 (12) 式中:α1,α2,…,αm,β1,β2,…,βn为常数系数;Ui,Li分别为xi的上界和下界,uj,lj分别为yj的上界和下界,均为常量。 设某次优化的初始解种群为R=(r1,r2,…,rk),当其中任意两个解之间的距离都不小于实数ε时,认为该初始种群足够分散。记任意两个解rc,rd在解空间中的坐标分别为(Xc,Yc),(Xd,Yd),其中rc,rd∈R,c,d (13) (14) 式中χ为种群大小,当种群中两个个体之间的距离过小时,可以随机调整其中某一个体某一维度的解,使其符合分散度要求。 古代军队行军时会通过驻扎休整来保持战力,由此得到启发,以进一步提高多决策变量优化算法的全局搜索能力。假设初始种群中有两个个体(如图3),基于2.2节种群初始化分散度的概念设计,结合种群个体的交叉变异范围,理论上能覆盖到尽可能多的可行解。然而在实际迭代过程中,个体某一维度的解不断逼近当前最优解,例如图3种群个体的X轴坐标在迭代中不断靠近最优个体坐标,个体的变异交叉范围虽然很大,但是迭代中实际能搜索到的可行解却很少。 (15) 率的最小值;h0为最大迭代次数;h为当前代数,初始化种群时h=0。初始化种群时的个体分散度高,迭代中丢失可行解的可能性更大,因此休整概率的初始值最大;随着迭代的进行,种群个体越来越密集,个体的搜索范围重叠度增加,可行解的丢失概率不断下降,休整概率相应下降。 工艺路线规划由多条工艺路线和多台工艺设备组合而成,在对其进行染色体编码时,需要采用实数编码方式将多段工艺路线染色体组合成一条染色体,作为与一种车间布局方案相配的工艺路线规划。如图4所示,每一条染色体分为m段,每一段从左到右的顺序表示一类产品的工艺路线,每一段的长度由该产品所需的工艺步骤数量决定,实数序号为每一步涉及的设备编号。 车间布局方案即设备布局方案,主要由各个设备的布局坐标组成,整段编码由2n个实数组成,n为车间的设备数量,前n个实数依次表示各个编号设备的横坐标,后n个实数依次表示各个编号设备的纵坐标,如图5所示。 因为该模型涉及设备的布置方向,所以除了上述两段编码,还需对n台设备的布置方向进行n维0-1编码。如图6所示,整段编码由n个0-1变量组成,依次表示各个设备的布置方式,1表示设备横放(即横长竖宽),0表示设备竖放(即横宽竖长)。 经典遗传算法中的进化算子包括选择算子、交叉算子和变异算子,其中交叉与变异算子用于实现遗传算法良好的全局搜索能力,选择算子尽可能地为交叉和变异提供良好的父代染色体,即增强寻优能力。在求解车间布局方案中,已经使用寻优能力极强的粒子群算法,在工艺路线的优化求解中应充分接受劣解以进一步提高整体解的全局搜索能力。因此在工艺路线规划解的迭代进化过程中剔除了选择算子,只保留提高全局搜索能力的交叉和变异算子。 因为工艺路线规划染色体由不等长的多段染色体组成,分别代表不同产品的工艺路线,所以交叉过程中禁止不同段染色体之间交叉,每一段染色体只能与与其对应的同段染色体交叉。如图7所示,因为交叉操作的意义在于交换彼此染色体包含的信息,而路径规划问题中的单一节点没有任何实际意义,至少需要两个节点才能构成路径信息,所以两条染色体中的同段染色体之间选择两点交叉的方式。 同理,由于不同段染色体代表不同产品的工艺路线,变异过程也不允许发生在不同段染色体之间。如图8所示,交换发生变异的同段染色体中的两个节点构成新的染色体。与一般染色体变异不同,该染色体的每一段都有相同的变异概率,即n段染色体有n次变异的可能,从而大大提高了全局搜索能力。 粒子群优化算法中解的更新方法为:以粒子个体的历史最优位置和种群历史最优位置为参考,通过改变粒子速度对种群个体进行动态调整。在上文提到的工艺路线规划不断变化的情况下,即使某一代解的车间布局方案足够好,也会因工艺路线规划变化引起适应度变化而自动跳出车间布局方案的局部最优解,因此对于车间布局部分的粒子群更新并不需要进行过多的优化处理。更新方法的具体内容如式(16)和式(17)所示: vi=wvi-1+j1rand(0,1)(pi-1-oi-1)+ (16) oi=oi-1+vi。 (17) 式中:vi表示各个车间布局种群个体的速度,为矢量;w为继承上一代种群个体速度更新的程度,w较大时算法的全局搜索能力较强,w较小时局部寻优能力较强,与上文提到的加强遗传算法的全局搜索能力相应,该算法应着重体现其局部寻优能力,因此应将w设置得相对较小;pi为每个个体历史最优的设备布局方案粒子;oi为某个设备布局方案粒子;gi为种群全局最优的设备布局方案粒子;j1,j2为粒子向历史最优与全局最优学习的程度,通常设j1=j2=2。 对采用二进制编码的设备布置方向种群适合用遗传算法变异算子中的单点变异方法进行迭代更新,如图9所示。其中,每次迭代中发生变异的染色体节点应不超过一定数量,以避免过多变异导致车间布局的最优解被掩盖。 根据以上对多决策变量优化算法的分析与设计总结算法流程,如图10所示,具体步骤如下: (1)对工艺路线种群、车间布局种群和设备布置方向种群进行初始化。 (2)对工艺路线种群与车间布局种群的种群分散度进行判定与优化,达到初始化种群分散度的要求后执行(3)。 (3)对工艺路线种群和车间布局种群的工艺约束和布局约束进行判定修正,即符合特定工艺顺序需求,同时设备间距大于零且各设备不超出车间边界才能执行(4)。 (4)计算初始化种群的适应度,对个体和全局最优种群(p和g)进行初始化赋值。 (5)判断是否执行种群休整,是则在后续迭代更新中跳过(7),否则依次执行以下步骤。 (6)对工艺路线种群进行交叉和变异操作,完成工艺路线种群进化。 (7)对车间布局种群的更新和设备布置方向进行变异操作。 (8)再次对工艺路线种群和车间布局种群的工艺约束和布局约束进行判定修正,完全符合约束后执行(9)。 (9)计算种群适应度,并更新个体与全局最优种群。 (10)判断是否达到最大迭代次数,是则结束该优化过程,否则重复(5)~(9)。 将问题描述中提到的A车间作为实例对象对模型和算法进行验证。该柔性车间进行设备布局规划的面积为长90 m、宽50 m,生产涉及的产品种类共11项,历史产量与预测量以及所含工艺步骤如表2所示,其中产品产量按20件为一托盘折算为托盘数。已知更换一台加工设备模具产生的物流量为0.17托/h,以设备一天工作20 h,一年工作300 d计算得一台加工设备一年的换模物流量为1 020托/年。另外,该柔性车间以潜入式自动导引小车(Automated Guided Vehicle,AGV)为主要运输方式,该AGV的动力电池为锂电池,参考文献[24]可得单位物流成本系数c=0.083元/m。各类产品、产量及其工艺步骤如表2所示。 表2 各产品相关产量与工艺步骤表 该车间生产涉及的工艺设备共15种,其中多种设备可采用不同的加工工艺,如表3所示。各设备区域面积如表4所示。 表3 各工艺步骤柔性约束 表4 各设备区域面积的长和宽 以MATLAB为运算环境,设定变异概率为0.9,交叉概率为0.1,继承系数为0.4,学习系数为0.6,根据2.1节内容,为了进一步增强遗传算法的全局搜索,将交叉概率从0.05提高到0.1,同理为了进一步加强粒子群算法的局部寻优,将继承系数从0.5下调至0.4,而将学习系数从0.5提高到0.6;对于休整概率的选取,在考虑到算法优化速度的情况下,选择初始值0.7和最小值0.3。最后,将3.1节实例数据作为多工艺路线与车间布局联合优化模型的输入,进行30次最大迭代次数为300的优化算法计算,结果如表5所示。其中最优值即最低年物流费用为4 035 838元,其优化迭代的收敛曲线如图11所示。最优工艺路线规划如表6所示,所得最优车间布局简图如图12所示。 表5 多工艺路线与车间布局联合优化结果统计表 元 表6 最优多工艺路线规划 续表6 3.3.1 多工艺路线已确定的车间布局优化 为了验证工艺路线与车间布局联合优化的必要性,将工艺路线作为模型固定参数输入(即多工艺路线已经规划完毕),同样对该车间布局进行30次优化计算,结果如表7所示。 从最优值看,表5中多工艺路线与车间布局联合优化方法的最优值为4 035 838元,表7中考虑工艺路线车间布局优化方法的最优值为4 527 334元,前者最多每年节省约49万元物流费用。从平均值看,表5中联合优化方法的年物流费用平均值4 594 768元比表7中考虑工艺路线的车间布局优化方法的年物流费用平均值4 769 548元节省约18万元。两种优化结果的对比如图13所示,统计结果如表8所示。 表7 考虑多工艺路线的车间布局优化结果统计表 元 表8 两种优化的统计结果 3.3.2 算法性能对比 将上述联合优化的运行结果作为多决策变量优化算法的优化结果,同时采用粒子群优化算法和遗传算法对实例进行整合编码设计并优化求解,对3种算法性能进行对比,如表9所示。因为时间在实际规划设计中相对充裕,所以没有对比优化迭代时间。3种优化算法的平均优化结果和对比如图14所示。 表9 3种优化算法的30次优化结果 元 表10 3种优化算法的平均优化结果统计表 多工艺路线与车间布局联合优化模型是以降低总体物流成本的车间布局方法为基础,结合柔性车间三大工艺柔性特点,对多工艺路线和车间布局进行同步优化,具有广泛适用性的设计方法。本文将多工艺路线规划和车间布局规划均作为模型的决策变量,根据不同产品的订单量决定该种产品工艺路线在总体规划中的影响程度,同时将与日常制造生产密切相关的出入库物流和换模物流纳入总体物流成本的考量之中,以使该模型更加贴近实际生产情况。通过实例验证,多工艺路线与车间布局联合优化模型求解的平均结果优于分别优化的平均结果,证明了该联合优化模型的可行性。 算法是求解数学模型的工具,为数学模型设计符合其特点的算法具有必要性[14]。多工艺路线与车间布局联合优化模型的求解特点在于,两种变量可以在各自维度上对解进行搜索。本文针对该问题提出多决策变量优化算法,当初始种群的量与分散度足够大时,在解的两个维度上分别采用具有全局搜索特点与局部寻优特点的算法,从而在对函数目标值快速求解的过程中保持较强的全局搜索能力,实例验证通过采用T检验对两种优化结果的平均值进行验证,在全局搜索和局部寻优两个角度证明了该联合优化算法的适用性和有效性。 智能工厂建设的浪潮刚刚兴起,对智能柔性车间规划进行设计优化的需求会越来越大,多工艺路线与车间布局联合优化模型是将工艺路线和车间布局联合优化的初步尝试,而与车间布局优化相关的规划设计不只有工艺路线,有必要构建整体性、系统性的智能工厂设计理论,与此相关的多元非线性约束优化算法也是需要进行深入研究的领域。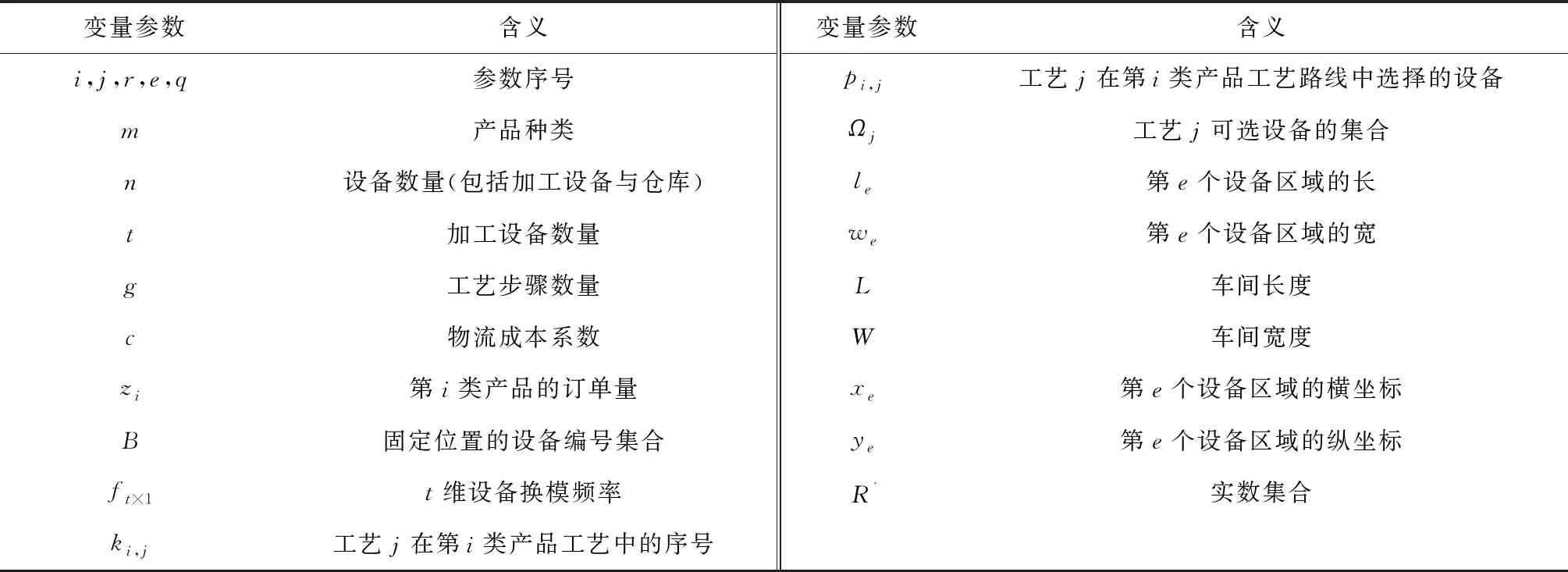


1.3 模型参数
1.4 数学模型
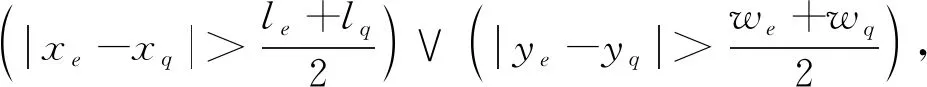

2 多决策变量优化算法设计
2.1 基于智能优化算法的多决策变量模型求解
2.2 初始种群的分散度
(α1L1+α2L2+…+αmLm);
(β1l1+β2l2+…+βnln);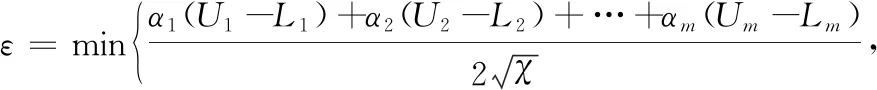
2.3 种群休整
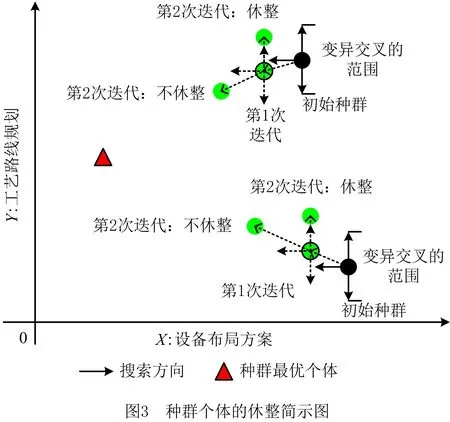
2.4 编码
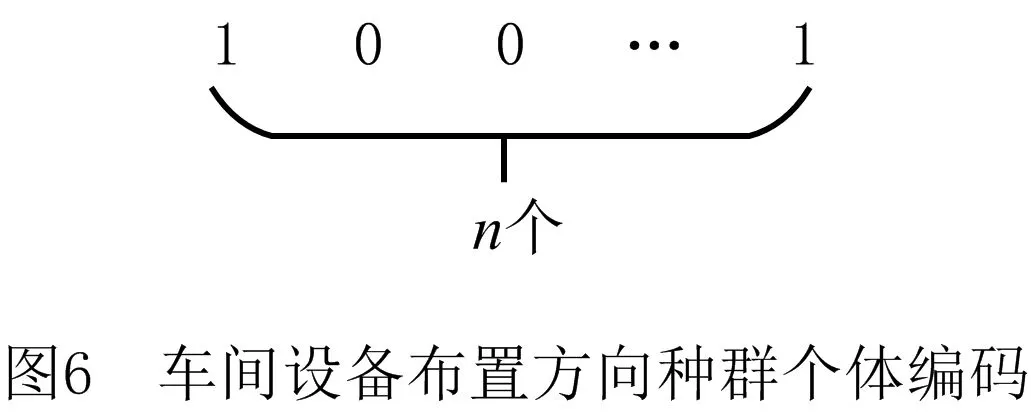
2.5 进化与更新
j2rand(0,1)(gi-1-oi-1);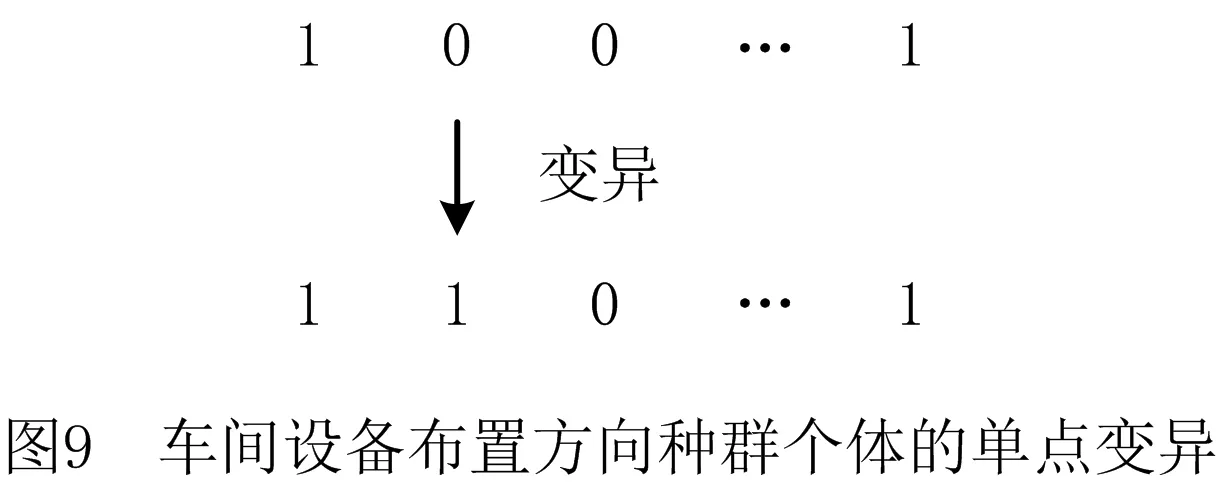
2.6 多决策变量优化算法步骤与流程
3 实例验证
3.1 实例数据


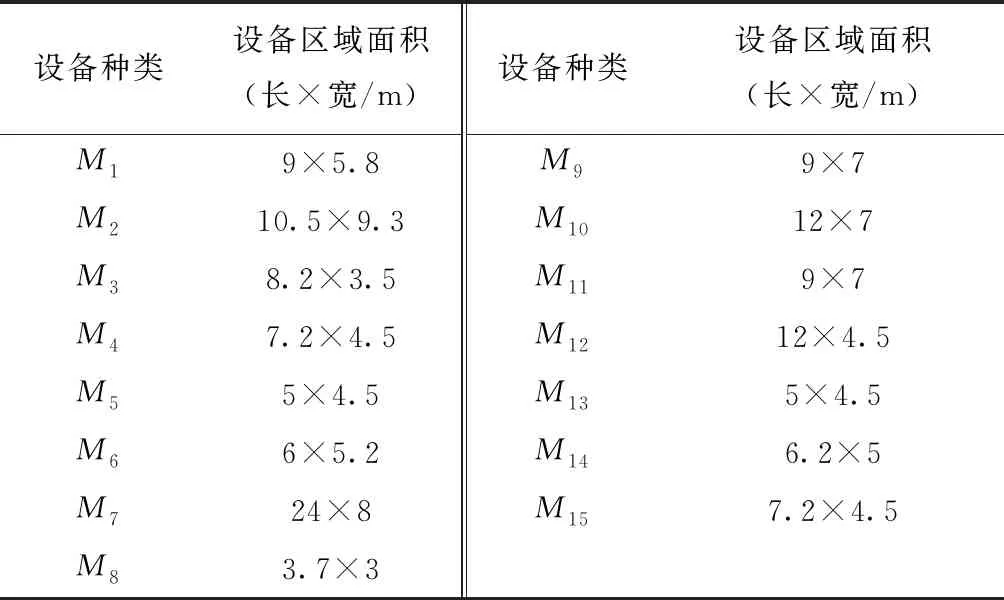
3.2 输出分析
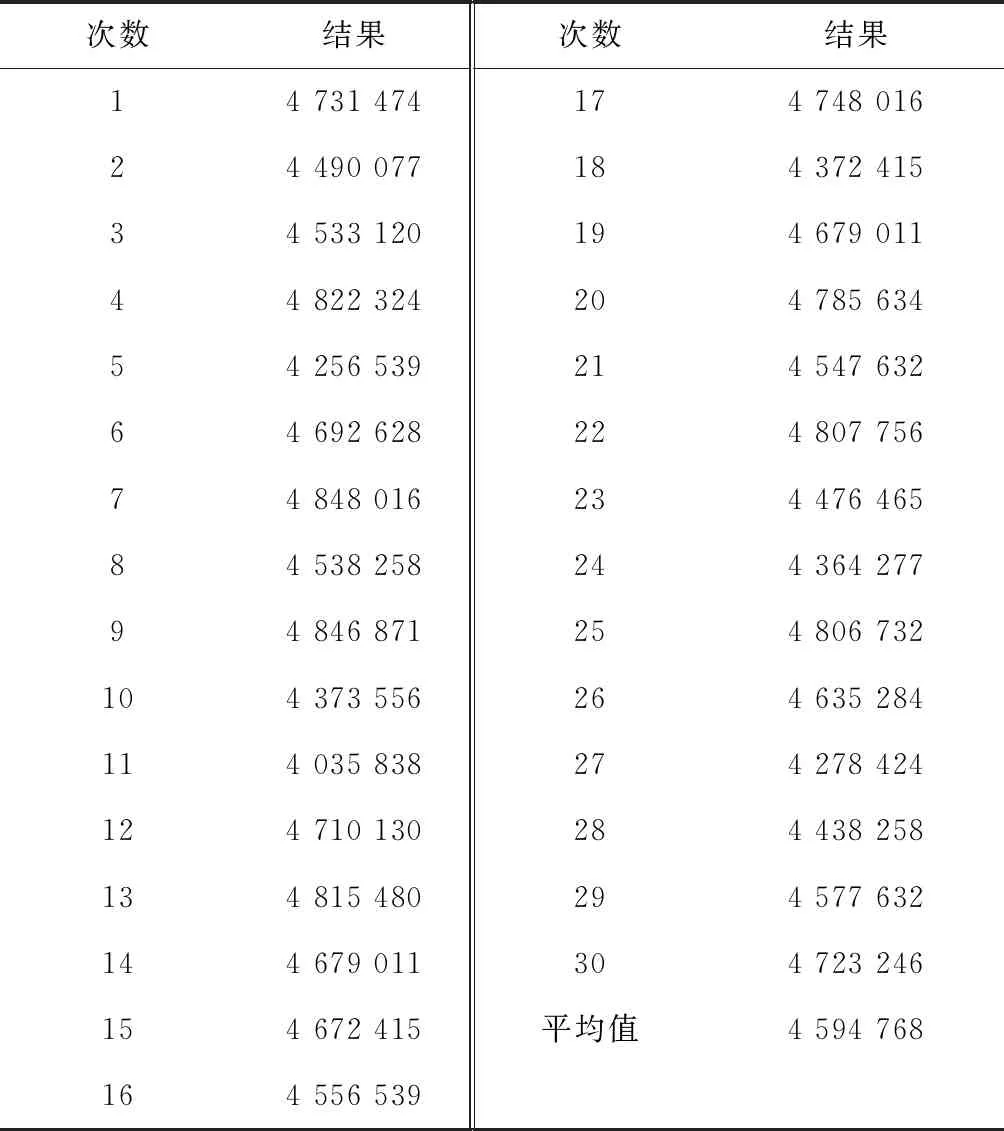
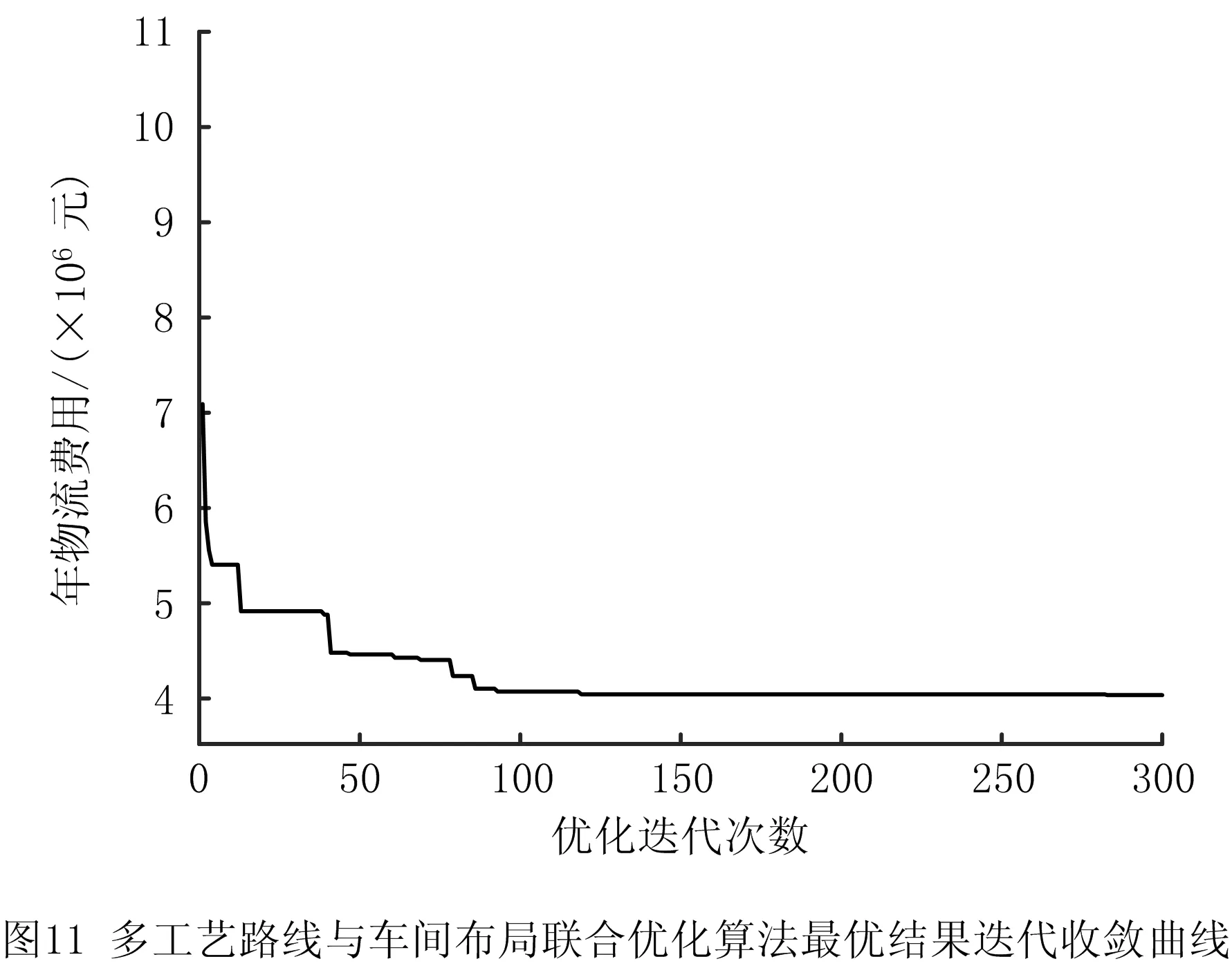


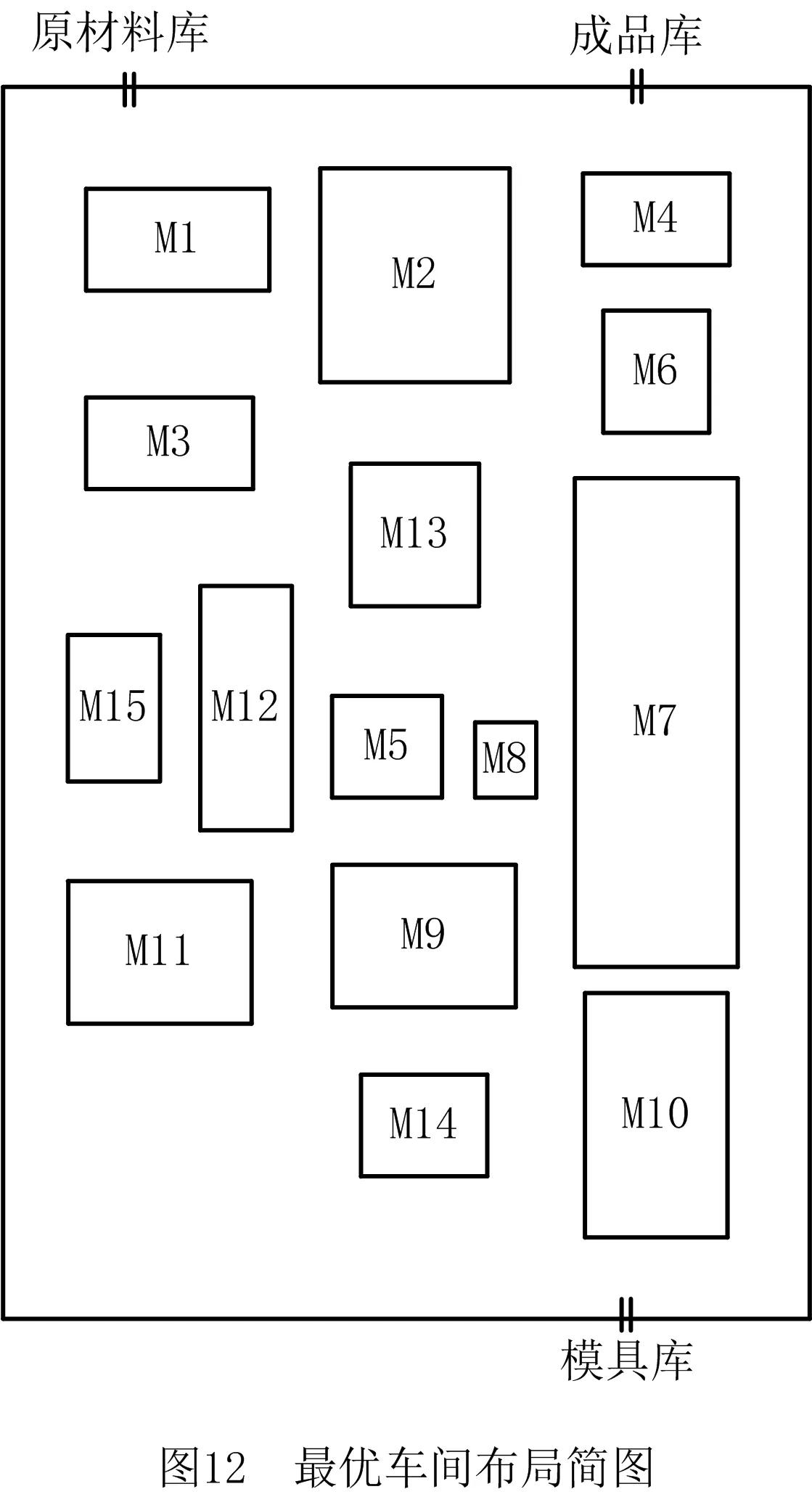
3.3 对比分析



4 结束语
