四旋翼不确定干扰前馈补偿与反步滑模姿态控制

薛晶勇，杨 波，朱永乐，王斌锐+

(1.中国计量大学 机电工程学院，浙江 杭州 310018；2.浙江运达风电股份有限公司，浙江 杭州 310012)

0 引言

在风力发电机组检测中，多旋翼无人飞行器对投放风电叶片检测机器人和监测风力发电机组的运行状况发挥着重要的作用[1]。为了提高发电量，风力发电厂一般建设在风资源充足的地区，加上多旋翼系统自身的非线性因素，给改善多旋翼无人机在不确定干扰下保持悬停并进行姿态跟踪的系统动态性能带来了挑战。

非匹配不确定性问题导致多旋翼在携带风电叶片检测设备或受到外部不确定干扰时表现不佳[2-4]。有效消除由外部不确定干扰与系统参数不确定综合产生的非匹配不确定干扰，是多旋翼无人机能够在风力发电机组在线监测、风电叶片检测机器人精准投放、高危泥石流环境救灾等领域进一步推广所必须面对的问题。滑模控制是解决带外部干扰的非线性系统控制问题的重要方法之一，大多数滑模控制方案可以完全消除系统模型中确定界的匹配干扰，保持系统稳定[5-8]，而对于不确定界的干扰则无法满足控制要求。对于非匹配不确定问题，反步法具有明显的优越性[9-10]，然而其微分爆炸问题使实际数据运算不准确，而且鲁棒性不强[10-12]，因此单一的反步法设计不适用于干扰环境下的多旋翼无人机控制。有学者结合反步法和滑模控制两者的优势，设计反步滑模控制方法，通过反步法将高阶系统分解为多个一阶子系统，从而将综合到最后一个子系统中的高阶系统干扰转化为一阶匹配干扰问题，用滑模控制方法进行设计[13-15]。然而，反步滑模的设计方法仍不能满足不确定界干扰的控制要求。对于系统存在不确定界干扰的问题，LABBADI 等[16]采用自适应方法估计干扰界，设计了自适应反步滑模控制器，由于其自适应参数位于滑模增益处，为了获得较强的鲁棒性而采用符号函数的形式。自适应方法适用于不确定干扰界为常值的情况[17-20]，对于具有时变特性的不确定界干扰系统，采用自适应方法难以保证系统的瞬态性能。

针对以上研究，本文通过反步法将四旋翼二阶姿态系统分解为两个一阶子系统，将二阶姿态系统的不确定问题转化为姿态系统第二子系统中的一阶匹配不确定问题，进而通过非线性干扰观测器(Nonlinear Disturbance Observer，NDO)观测并估计不确定干扰，将干扰的估计量进行前馈补偿，设计反步滑模姿态抗干扰控制器，从而提高控制器的鲁棒性，该控制策略使四旋翼系统在具有时变特性的不确定界干扰下具有良好的动态性能。

1 四旋翼系统动力学模型

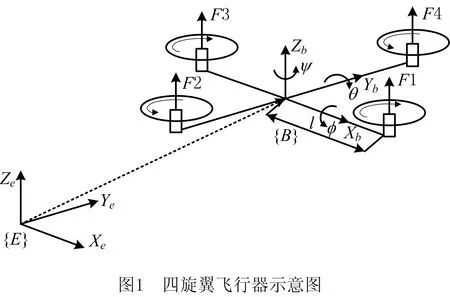
图1所示为四旋翼飞行器示意图。图中，E=(Xe,Ye,Ze)为地面坐标系，B=(Xb,Yb,Zb)为机体坐标系。在地面坐标系下定义ξ=[x,y,z]T和η=[φ,θ,ψ]T为四旋翼的位置向量和姿态向量。地面坐标系到机体坐标系的转化矩阵为

(1)

飞行器的速度向量V=[u,v,w]T，机体坐标系下的角速度向量Ω=[p,q,r]T，基于牛顿—欧拉方法建立如下带不确定干扰的四旋翼动力学模型：

(2)

式中：m为四旋翼总质量；TB为总体提升力向量；GE为重力加速度项；d为外部干扰力；W为由机体坐标系下的姿态表示到地面坐标系下的姿态表示的转化矩阵；J=diag(Jxx,Jyy,Jzz)为转动惯量；ΔJ为系统转动惯量矩阵中的未知部分；MB为机体坐标系下的控制力矩；D为外部干扰力矩；U1为总提升力；Fi为第i个电机的提升力；CT为螺旋桨升力系数；ωi为第i个电机的转速；l为电机轴线到四旋翼质心的距离；kd为阻尼力矩系数。

2 非线性控制器设计及稳定性

风力发电机组所在场地风资源充足，风场环境复杂多变，四旋翼系统在这种环境下运作将受不确定干扰影响，为了使四旋翼系统仍然具有稳定的姿态跟踪和位置跟踪性能，本文设计了一种新的非线性控制策略。

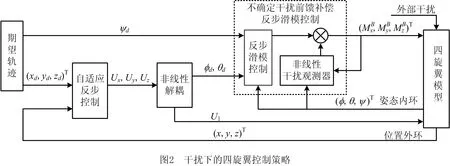
图2所示为干扰下的四旋翼控制策略，其中：外环为位置环，采用自适应反步滑模控制；内环为姿态环，采用不确定干扰前馈补偿的反步滑模控制。当系统受到不确定干扰时，姿态系统能够通过估计和补偿干扰来保持期望状态或快速跟踪期望状态，提高了四旋翼系统的鲁棒性。

2.1 基于自适应反步的位置控制

因为受外部环境影响，而且飞行状态持续时间短，位置环中的干扰大多表现为常值或慢时变干扰信号，所以位置环控制器设计采用自适应反步控制方法。

根据式(2)四旋翼动力学模型中的位置系统模型，假设位置系统中的干扰d满足范围有界，即满足

(3)

式中Δc为常量或慢时变量的未知上界。

设计位置环的第1个虚拟子系统

(4)

式中α1为虚拟控制量。

定义位置误差

e1=ξ-ξd。

(5)

对应位置环虚拟子系统(4)，选取Lyapunov候选函数

(6)

将式(6)两边对时间t求导，得

(7)

为了使子系统稳定，设计虚拟控制量

(8)

式中A1∈R3×3为正定对角矩阵。

将式(8)带入式(7)，得

(9)

因此位置环虚拟子系统全局渐近稳定。

根据式(2)中的第2个子公式，设立位置环第2个虚拟子系统

(10)

式中α2=[Ux,Uy,Uz]T∈R3为虚拟控制输出。

定义速度误差

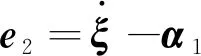
(11)

选取Lyapunov候选函数

(12)

将式(12)两边对时间t求导，得

(13)

为使位置系统稳定，设计虚拟控制输出

(14)

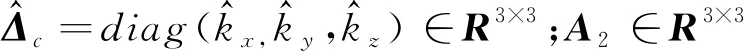
设计自适应律

(15)

式中β∈R3×3为正定对角矩阵。

定义估计误差

(16)

为了在设计的自适应律下保证系统稳定，结合式(12)设计Lyapunov候选函数

(17)

将式(17)两侧对t求导，得

(18)

通过对位置控制输出量进行非线性解耦，得到总提升力以及姿态环的期望滚转角和俯仰角。结合式(2)的第2个子公式和式(10)得到

(19)

基于式(1)和式(2)解得实际提升力、期望滚转角和俯仰角分别为：

(20)

2.2 干扰前馈补偿与反步滑模姿态控制

2.2.1 姿态环模型描述

根据式(2)，姿态在零位附近小角度变化范围下的姿态环模型可描述为：

(21)

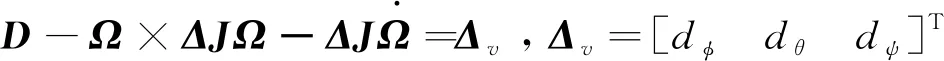
由于风场变化，而且四旋翼姿态系统中的参数存在不确定问题，作用在姿态环的总干扰上界不确定且具有一定的时变特性。这里采用非线性干扰观测器对这种不确定干扰进行观测估计，并结合反步滑模控制方法，在控制输出中以不确定干扰量的估计值作前馈补偿，使得四旋翼在不确定干扰下的姿态跟踪方面有较好的表现。

2.2.2 基于非线性干扰观测器的不确定干扰前馈补偿

由式(21)可知姿态环第2子系统为

=f(Ω)+J-1MB+Dv。

(22)

式中：f(Ω)=-J-1(Ω×JΩ)为系统非线性函数；Dv=J-1Δv。

假设不确定干扰相对以下设计的观测器动态特性是缓慢变化的，则有

(23)

定义估计误差

(24)

辅助变量

(25)

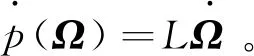
所设计的非线性干扰观测器的动力学方程为

(26)

因此非线性干扰观测器方程设计为：

(27)

为了保证不确定干扰估计值收敛，选取Lyapunov函数

(28)

将式(28)两端对t求导：

(29)

求解不等式方程式(29)，得

Vo(t)≤e-2L(t-t0)Vo(t0)。

(30)

由式(30)可见，非线性干扰观测器呈指数收敛，其中带宽L越大，收敛速度越快。

2.2.3 姿态抗干扰控制器设计

根据式(21)，设计姿态环第1虚拟子系统

(31)

式中α3为虚拟控制量。

定义姿态环中角度跟踪误差

e3=η-ηd。

(32)

选取Lyapunov候选函数

(33)

将式(33)两边对t求导，得

(34)

为了使姿态环第1虚拟子系统稳定，设计虚拟控制量

(35)

式中A3∈R3×3为正定对角矩阵。

将式(35)带入(34)，得

(36)

因此e3=0是全局渐近稳定的。

由式(22)可将姿态环第2虚拟子系统设计为

(37)

式中虚拟控制量α4∈R3。

设计姿态系统滑模面

结合式(27)非线性干扰观测器对不确定干扰进行估计补偿。为了验证姿态系统的稳定性，选取Lyapunov候选函数

(39)

将式(39)对时间t求导，得

(40)

(41)

将式(41)带入式(40),可得

∀e3≠0，S≠0,

(42)

因此姿态系统全局渐近稳定。

3 仿真分析

为了验证干扰前馈补偿下反步滑模姿态控制方法抗干扰的有效性，设计并进行了四旋翼系统应对不确定干扰的飞行数值仿真实验。以下是四旋翼飞行器在不确定干扰下的定点悬停和姿态跟踪仿真实验与仿真分析，表1所示为自主研发的四旋翼飞行器的物理参数。

表1 四旋翼飞行器性能参数

3.1 仿真条件及参数设置

本文的控制系统参数如下：

β=diag(0.5,0.5,0.5)，L=2.0,ε=0.3。

外部环境以及系统模型参数不确定造成的不确定干扰，包括常值干扰、风场的波动信号和撞击产生的阶跃信号。仿真中为了更直观地展现所设计的控制器在应对不同干扰时的飞行表现，将四旋翼在3个不同高度进行悬停。第1次悬停时，在位置系统中加入常值干扰力；第2次悬停时，在姿态系统叠加入常值干扰力距；第3次悬停时，在姿态系统加入波动形式干扰的同时叠加入高频噪声信号。所建模型如下:

为了模拟风场干扰的波动形式，取随机数-0.25≤Dr≤0.25，并以白噪声的形式输入。在t∈[0,20)∪(60,100]时，四旋翼所受的干扰力矩为0 N·m。

3.2 仿真结果及分析

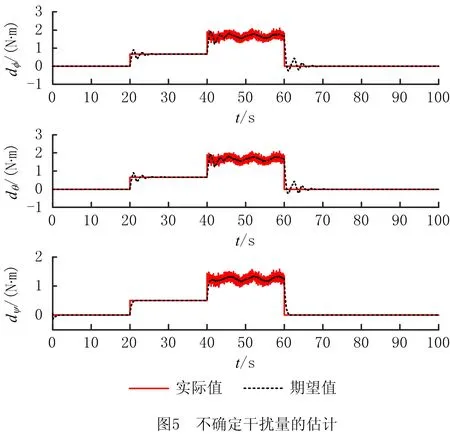
四旋翼系统中内环的姿态系统控制特性对整个控制系统的鲁棒性及动态表现至关重要。仿真中，在干扰前馈补偿机制下，分别在四旋翼3次不同高度的悬停阶段设计加入3次不同形式的干扰。表2所示为四旋翼悬停参数，图3所示为不确定干扰下的四旋翼悬停，图4所示为不确定干扰下的四旋翼姿态跟踪情况。

表2 四旋翼悬停参数

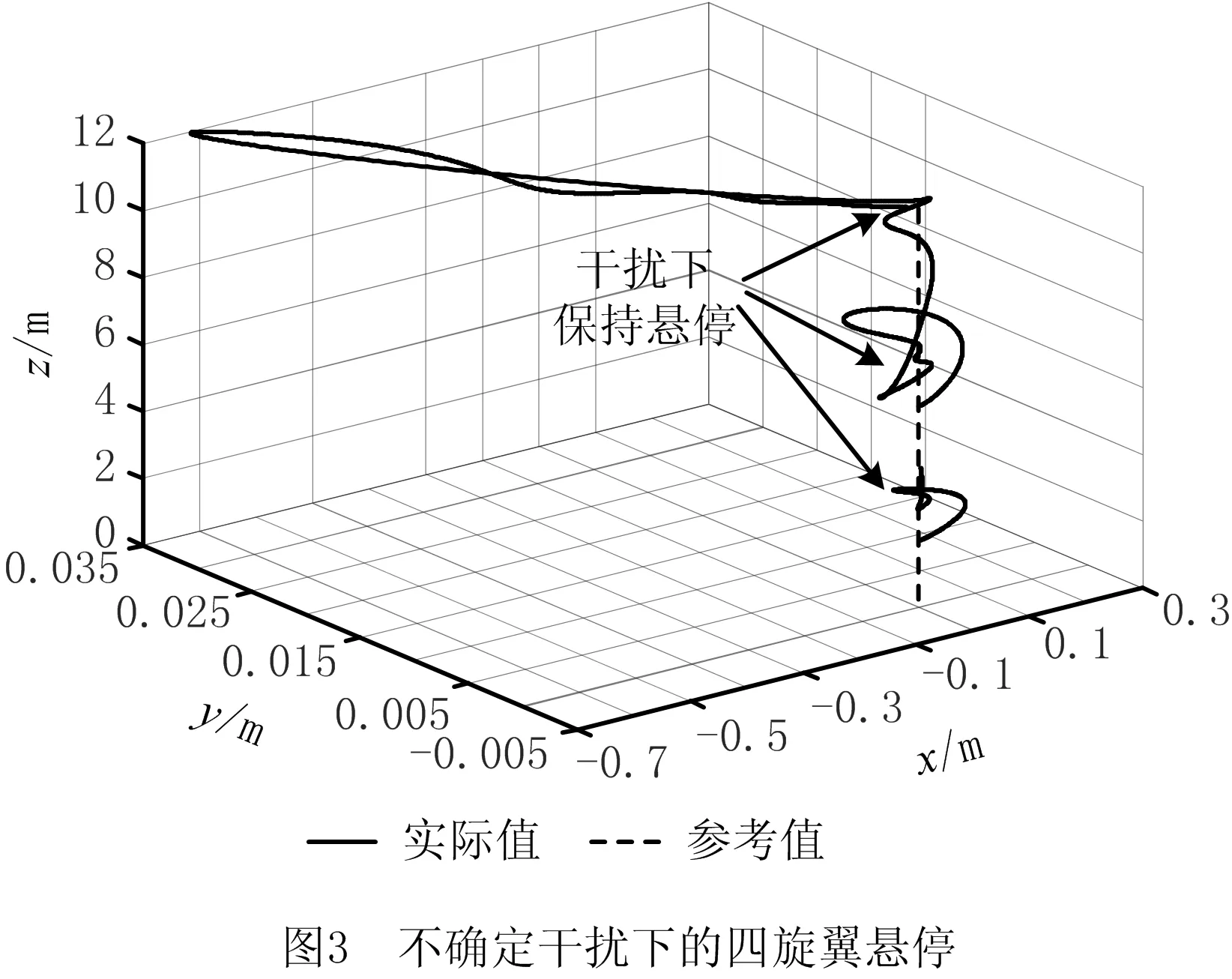
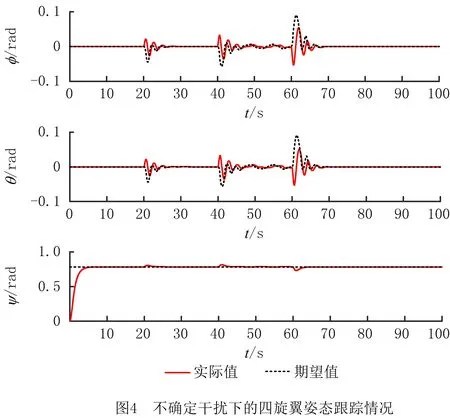
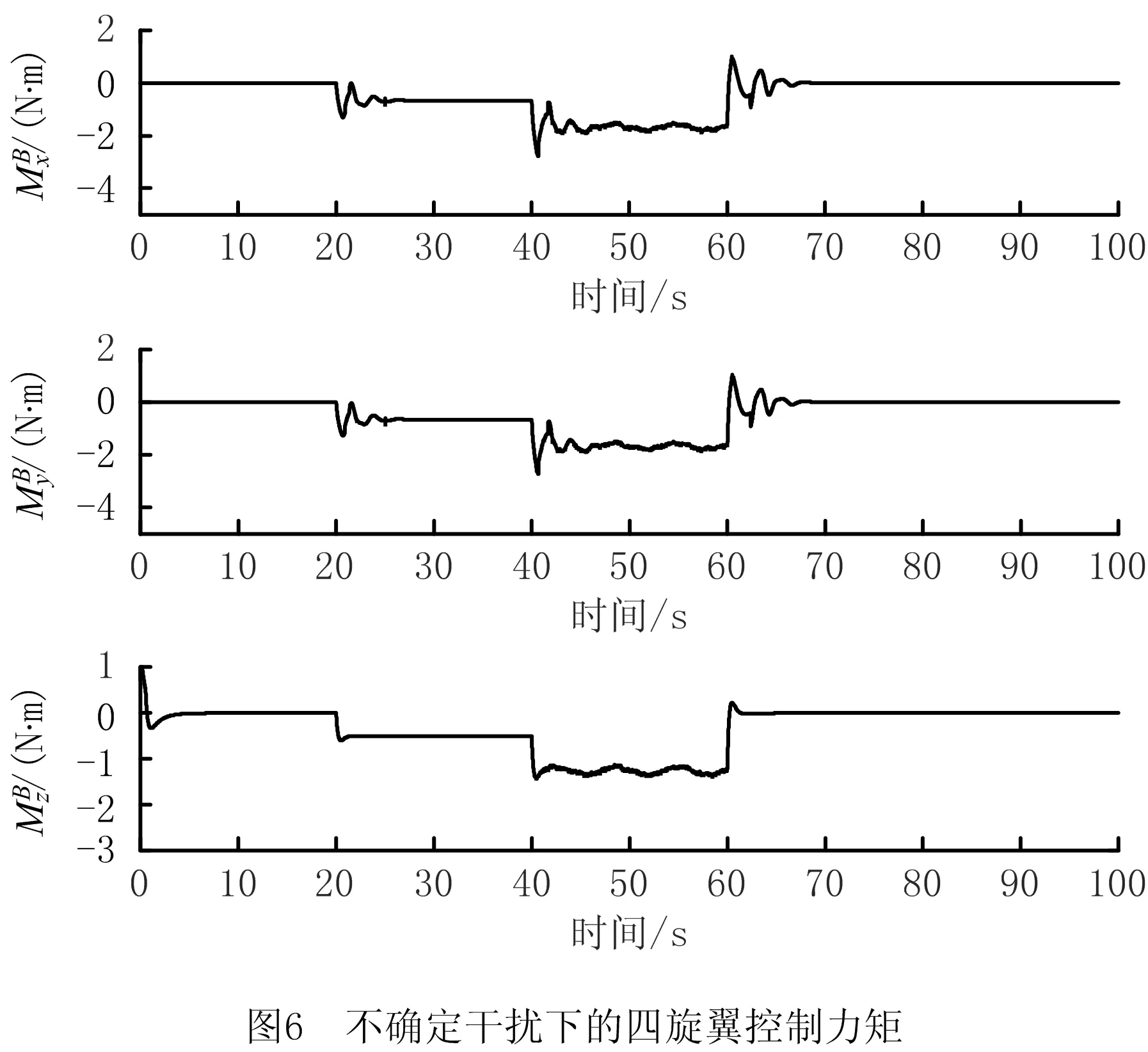
由图3和图4可见，在3次干扰下，处于悬停状态的四旋翼在3个方向产生偏差后，通过姿态系统调整四旋翼姿态来平衡不确定干扰，再通过位置系统使四旋翼运行到期望位置保持悬停。图5所示为姿态系统分别在20 s和60 s加入阶跃干扰信号、在40 s加入波动干扰叠加白噪声模拟风场的不规律波动信号时，非线性干扰观测器对不确定干扰进行实时估计，使干扰的估计值收敛到实际值。图6所示为不确定干扰下四旋翼控制力矩的输出曲线，可见非线性干扰观测器的估计量能够快速逼近干扰力矩的实际值，对控制量做出前馈补偿；同时，非线性干扰观测器的补偿量有效抑制了滑模控制输入量的抖振现象，使四旋翼控制系统的动态性表现良好。由图3和图5可见，在前馈补偿量收敛后，常值干扰对四旋翼的位置控制外环无明显影响，加入阶跃干扰信号或波动干扰叠加白噪声信号后，在开始5 s内姿态收敛至期望姿态附近。结合图6可见，在不确定干扰信号下，姿态子系统通过干扰的估计量和当前状态计算出当前所需的控制力矩，以此平衡不确定干扰，使飞行器姿态迅速达到稳定状态，验证了在飞行器保持悬停的飞行任务中，采用该控制方法能够保证四旋翼飞行器优越的抗干扰特性。同时，根据图6姿态系统输出控制力矩的表现，证明了所设计的抗干扰控制策略不是通过较高的切换增益来实现。在实际电机控制中，电机动态响应速度无法达到较高切换增益下的控制效果，因此所涉及的控制方法具有实用性。

通过上述仿真分析可见，采用非线性干扰观测器的估计量前馈补偿结合反步滑模控制方法，能够有效解决由外部环境变化或飞行系统内部参数不确定导致的四旋翼系统高阶不确定干扰问题，证明了所设计的四旋翼控制策略应对阶跃干扰、波动干扰信号和白噪声模拟的随机干扰的有效性与鲁棒性。

4 实验与分析

本章采用自主研发的风力发电机组在线检测四旋翼飞行器，在外部干扰下进行飞行实验，验证采用非线性干扰观测器的前馈补偿与反步滑模控制的四旋翼系统的抗干扰特性与运动性能。

如图7所示，将四旋翼飞行机器人悬停在3.0 m处，通过外部GPS位置信息使飞行器保持定点模式;四旋翼控制系统采用PIXHAWK控制器，将飞行信息实时记录到SD卡中;上位机实时显示外部风场干扰的大小，并保存数据。

图8所示为轴流式风机营造的模拟的风场环境。当四旋翼起飞进入到定点悬停状态后，于24 s开启轴流式风机，以此模拟风场干扰。轴流式风机营造的局部风场环境，平稳后的风速约为6 m/s～7 m/s，根据风力等级表，测试环境风力达到4级强度。

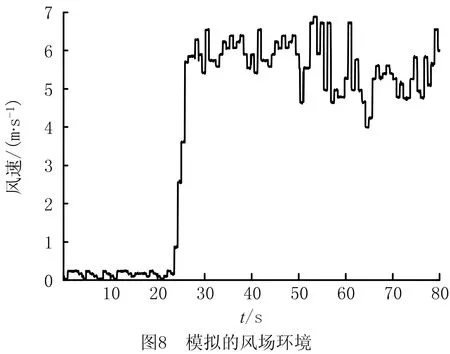
由图8可见，24 s后局部风场风速加强，28 s左右达到局部4级风场环境，之后风场一直处于波动状态。图9所示为不确定干扰前馈补偿下的四旋翼飞行表现。由图9a可见，四旋翼飞行器在27 s左右，受风场影响滚转角和俯仰角发生明显变化；在30 s左右，四旋翼飞行器的姿态角收敛，姿态系统达到稳定状态。

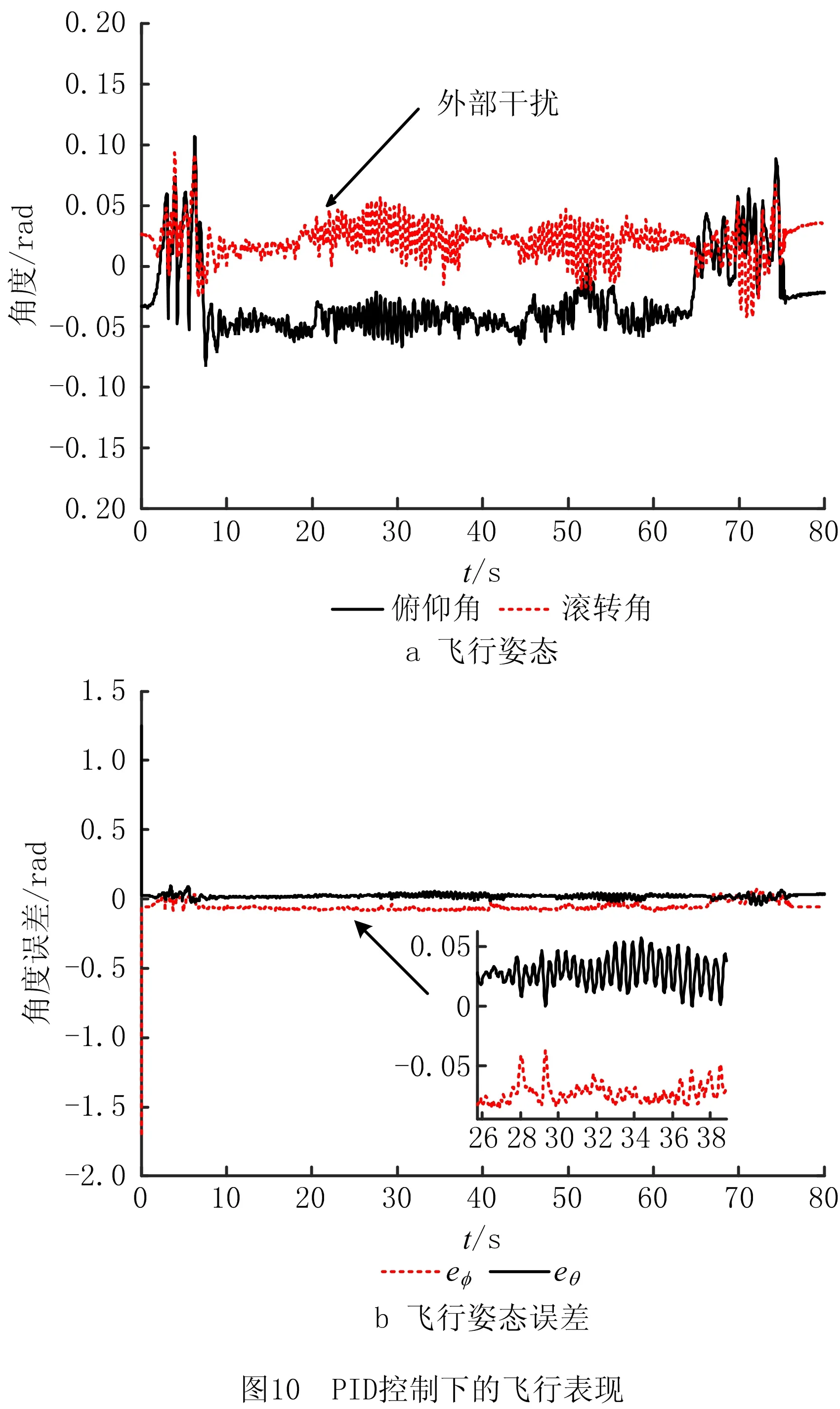
对比图9a与图10a、图11a不同模式控制下飞行姿态的收敛趋势可见，在受到外部突变风场干扰时，四旋翼飞行器姿态系统可在较短时间内保持稳定。相比图10aPID控制下的四旋翼飞行器飞行姿态受到干扰时的动态特性，所设计的基于非线性干扰观测器对不确定干扰的前馈补偿与反步滑模控制相结合的方法，有效提高了在阶跃干扰信号和风场波动干扰下飞行机器人的抗干扰性。与图11a反步滑模控制下的飞行姿态相比，设计前馈补偿机制的反步滑模控制方法可以有效提高四旋翼飞行器系统干扰下的的稳定性和姿态系统的收敛速度。对比图9b带有干扰补偿机制的反步滑控制下的飞行姿态误差与图10b和图11b两种控制方法下的误差可见，在干扰下，采用PID和反步滑模控制方法，姿态系统都会存在一定的稳定误差，收敛效果不佳，同时PID控制方法对外部干扰波动较敏感。所设计的前馈补偿反步滑模控制可以使误差较快收敛，而且在波动干扰下相比反步滑模控制下的姿态误差具有较好的收敛效果和动态特性。

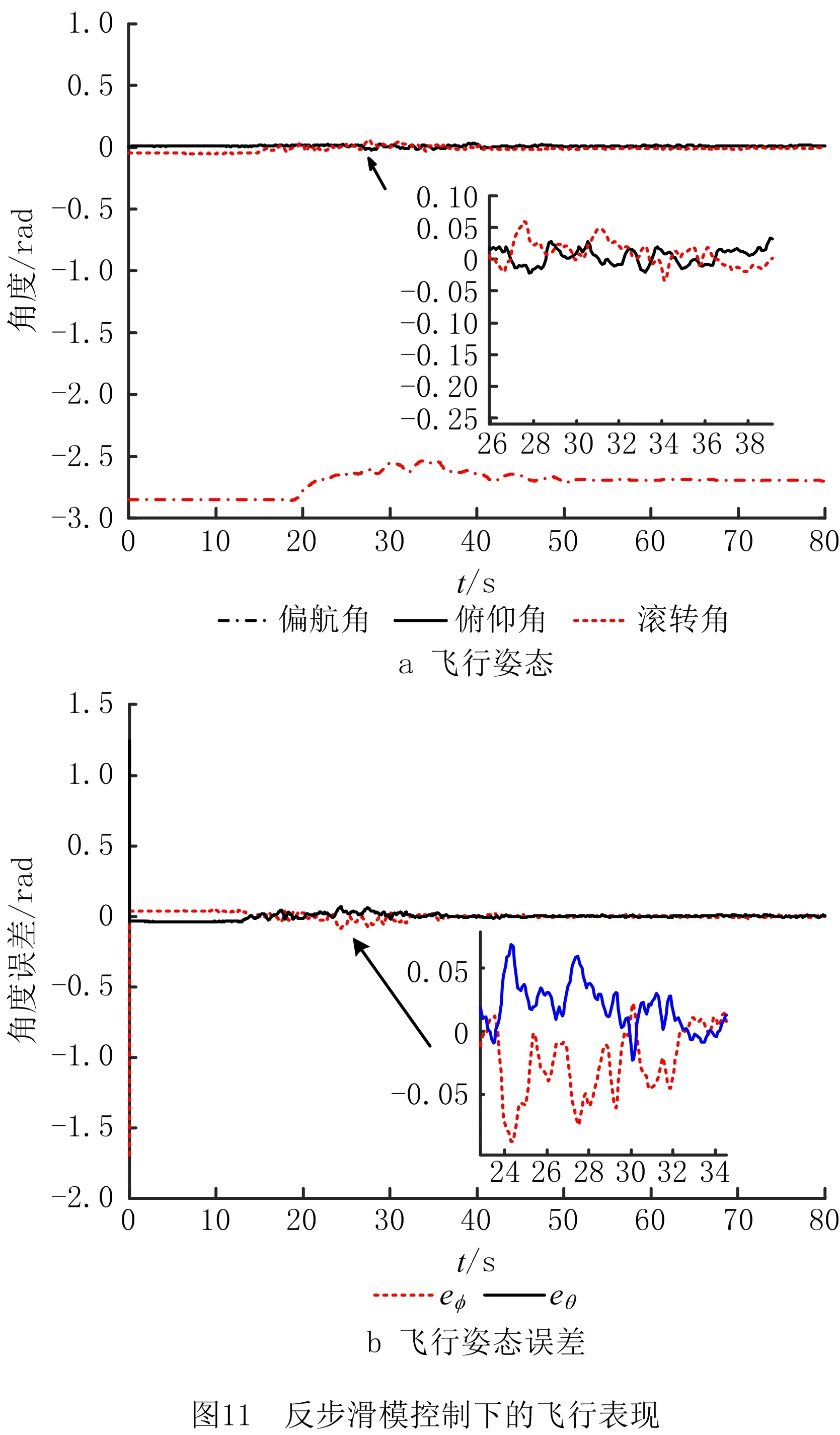
通过上述控制结果，分别采用PID控制方法、反步滑模控制方法和前馈补偿的反步滑模控制方法，归纳总结实际四旋翼飞行器姿态系统的稳定误差范围和均方根误差，如表3所示。

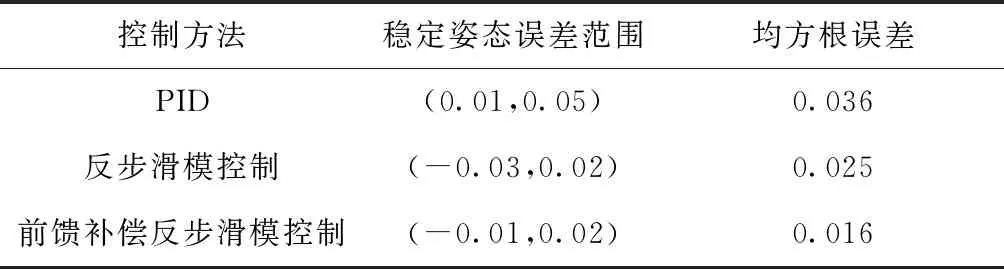
表3 抗干扰实验四旋翼飞行器姿态误差对比 rad

由表3可见，前馈补偿反步滑模控制下的姿态系统均方根误差比PID控制减小了56%，比反步滑模控制减小了36%。因此，干扰前馈补偿机制结合反步滑模的姿态控制方法，能够有效提高四旋翼飞行器的控制效果，并改善干扰下飞行器的可操作性能，同时验证了所设计方法在四旋翼系统姿态抗干扰控制策略中的有效性与实用性。实验采用的惯性测量单元(Inertial Measurement Unit , IMU)静态误差在0.01 rad左右，其随温度升高还有上升的趋势。因此，所设计的四旋翼姿态抗干扰控制方法，在实验测试过程中的控制精度与数值仿真中的不一致。但在相同硬件条件下，采用干扰前馈补偿机制结合反步滑模的姿态控制方法的四旋翼飞行器的控制精度最佳，与数值仿真的结果分析一致。

5 结束语

本文针对四旋翼控制中存在的有外部不确定干扰和系统参数不确定引起的具有时变特性的不确定界干扰问题，设计了一种四旋翼系统不确定干扰前馈补偿的反步滑模姿态控制方法，该方法通过非线性干扰观测估计，使估计量收敛到实际干扰量。结合反步滑模控制和干扰估计量的前馈补偿方法设计抗干扰姿态控制器，通过Lyapunov稳定性理论证明了系统的稳定性，最后通过仿真和实验验证了所设计方法应对阶跃或波动干扰信号的有效性和实用性。仿真结果同样验证了该方法的抗干扰特性并非通过滑模控制引入较高的切换增益实现，从而在一定程度上减小了引入滑模控制造成的控制输入不连续和系统抖振现象。

实际中，旋翼飞行器在线检测风电机组时，会在底部挂载风电叶片检测机器人等设备。为了在检测过程中保护风电叶片，需要在高阶不确定干扰下研究旋翼飞行器定高控制方法，同时在设计控制器时所能输出的控制量受限于电机最大提升力，下一步将研究控制量有限且不确定干扰下，悬挂负载的旋翼飞行器的抗干扰姿态控制问题。