基于多纵向传输通道的双层过道布置问题建模与优化

2022-03-11刘俊琦张则强龚举华

计算机集成制造系统 2022年2期

刘俊琦，张则强，管超，龚举华

(西南交通大学机械工程学院，四川成都 610031)

1 问题的提出

设施布局问题(Facility Layout Problem，FLP)是一种经典的运筹学难题，其以最小化物流成本为目标[1]对设施进行合理的组合排序，并作为当前制造业发展的重要内容，存在于多种类型的制造和服务系统[2-6]，如制造业中的生产车间布局[5]、服务业中的办公区域布局[7]、医院走廊两侧病房的安置[8]，布局优化是否合理直接影响作业效率和运作成本。因此，近几十年来，FLP一直受到制造业、服务业和学术界的广泛关注[9-10]。

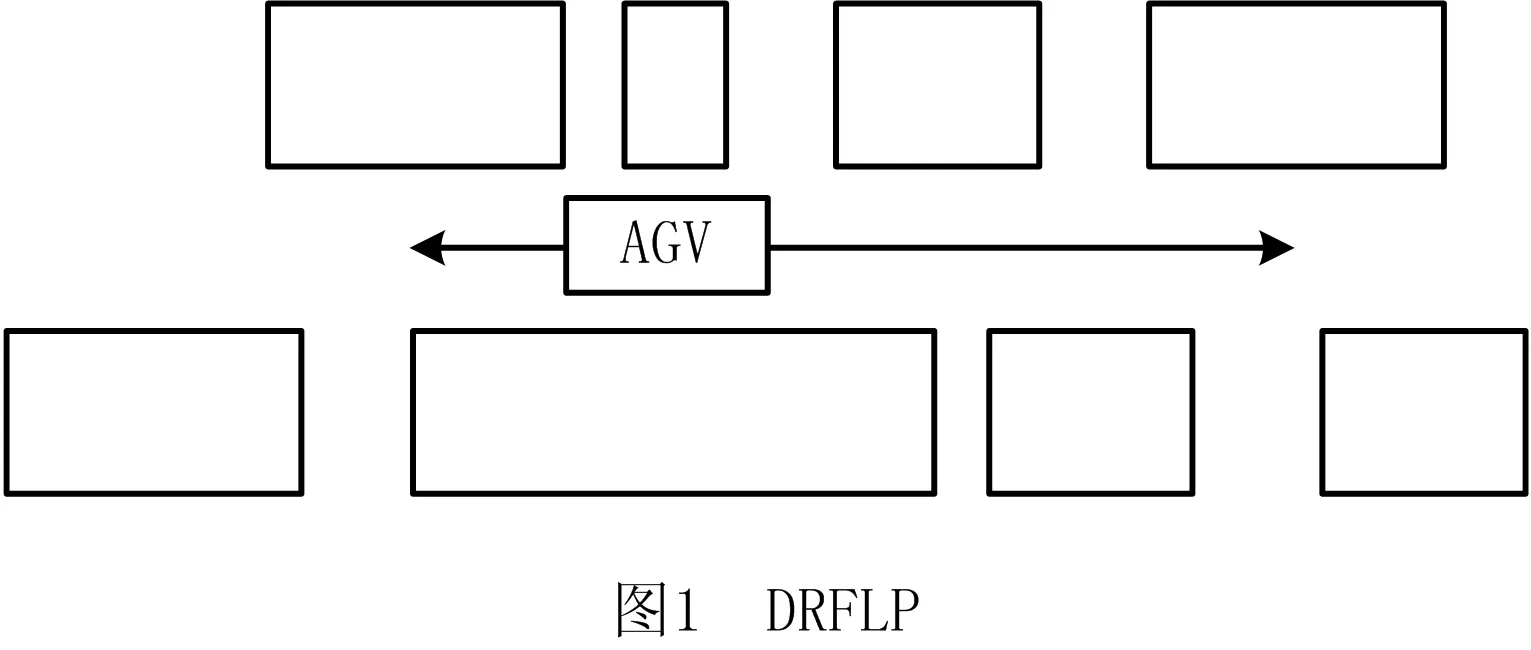
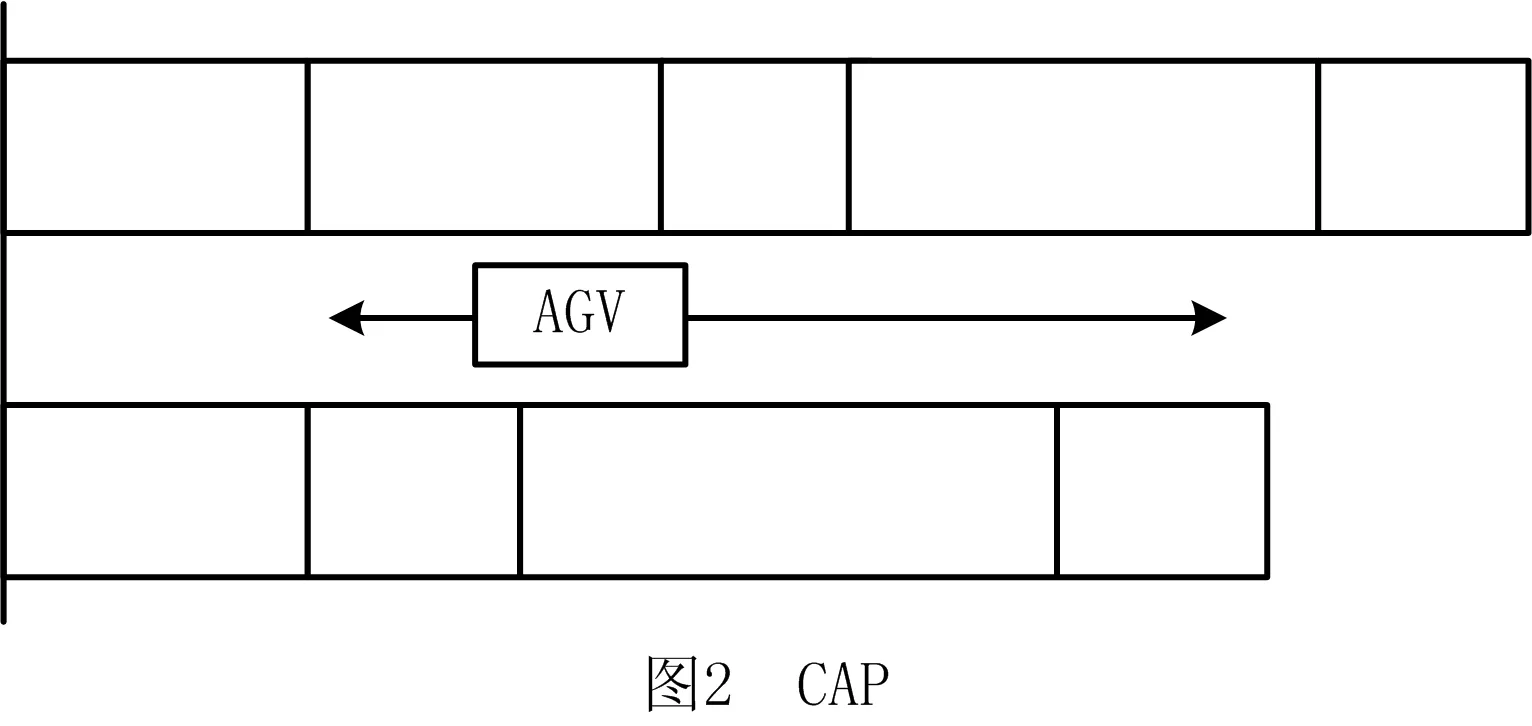
过道布置问题(Corridor Allocation Problem, CAP)[11]是FLP的一种形式，其模式与双行布局问题(Double Row Facility Layout Problem, DRFLP)[12-13]比较相似(如图1和图2)，两者的区别在于CAP遵循以下两个约束：①上下两行的布置起点均为通道的最左边，即坐标原点；②相邻两个设施之间没有间隙。CAP是一种典型的具有NP-hard属性的组合优化问题，扩大问题规模和增加约束条件均会大大增加精确求解的难度，由于具有较高的研究价值和广阔的实际应用前景，CAP自提出以来便快速成为设施布局领域的研究热点。

AMARAL[11]于2012年首次提出并建立了CAP的混合整数规划(Mixed Integer Programming, MIP)模型，并以设施间总物流成本最小为优化目标提出3种启发式算法，分别对其进行求解测试，验证了该模型的正确性和算法的有效性；GHOSH等[14]采用改进遗传算法和分散搜索算法(Scatter Search, SS)分别对CAP的不同规模问题进行测试，进一步提高了求解该问题的运算效率；AHONEN等[15]分别采用禁忌搜索(Tabu Search,TS)算法和改进模拟退火(Simulated Anneal, SA)算法对CAP大规模问题进行求解，两种算法均可得到当前最优解，经对比，改进SA算法在求解效率和求解质量上均优于TS算法；KALITA等[16-17]在原始CAP模型的基础上，考虑通道总长度，在原CAP模型中增加最小化通道长度的优化目标，建立了非线性双目标优化问题数学模型，即设施总长度与设施间物流总成本最优，并分别应用基于序列置换遗传算法和改进遗传算法对标准算例进行测试，验证了两种算法的有效性。上述文献研究的CAP均为单层问题，然而在实际工业制造领域或服务部门中，当设施数量过于庞大且布局面积受限时，为了提高空间利用率、降低成本，越来越多的多层空间布局被采用，为了更好地结合实际情况，管超等[18]提出并构建了双层过道布置问题(Double Floor Corridor Allocation Problem ,DFCAP)MIP模型，随后采用花授粉算法进行求解[19]，验证了所提MIP模型的正确性以及算法的有效性；为了更好地贴合实际，管超等[20]在初始DFCAP的基础上考虑通道宽度对CAP的影响，建立了混合整数非线性规划模型，并采用改进SA算法进行算例测试，结果表明改进抽样过程的SA算法能够很好地求解所提问题。随着多楼层设施布局在实际生产生活中应用的增多，而且传统单货梯存在一定的运输成本浪费，越来越多的智能加工车间采用多纵向传输通道运输的方式，如图3所示(某企业多通道双层纵向运输机)。参考已有文献,尚未发现有关多纵向传输通道运输方式CAP研究的报道，因此本文以DLCAP为基础，提出一种基于多纵向传输通道的拓展双层过道布置问题(Extend Double Floor Corridor Allocation Problem ,EDFCAP)，并采用LINGO优化器对所提模型进行精确求解，为后续模型与算法的验证提供理论依据。

SA算法和TS算法为近年来国内外均比较关注的算法[15,21-22]，两种算法在求解NP-hard属性问题上均具有良好的求解性能，如路径规划问题[23-24]、0-1背包问题[25-26]和车间调度问题[27]等。除此之外，两种算法均在CAP方向得到广泛应用，如CAP[15]、圆环CAP[28]。传统的TS算法利用禁忌表锁住部分最优解，有意识避开已找到的局部最优解，从而搜索更多区域，其全局能力较强，但对初始解的要求较高，而传统SA算法对初始解的要求则不高。因此，结合问题特征，本文根据两种算法的特性和优点对两种算法进行混合改进(带有禁忌搜索操作的模拟退火算法(Simulated Annealing algorithm with Tabu search, TSA))，使其在降低初始解的前提下提高全局搜索的概率。最后，为更好地说明所提算法的性能，将TSA与多种算法求解不同类型CAP的结果对比，表明TSA在求解精度与效率方面更胜一筹。

2 考虑多纵向通道的EDFCAP数学模型

2.1 问题描述

本文旨在考虑设施布置在场地所用面积有限及单一纵向运输通道存在浪费等问题对设施布局的影响，在文献[17]的基础上提出基于多纵向传输通道的EDFCAP。在基本DFCAP中，两个楼层之间的交互通道为最左侧的货梯，而EDFCAP是在2层的每一个物流交互点处设置一个与1层交互的纵向通道，并在每个通道处安装往复式升降机(如图4)，而且纵向运输通道数量与上层设施数量相同。EDFCAP同初始DFCAP一样，分别在1层和2层通道的左右两侧布置设施，并按照设施之间的物流关系对设施进行排序，从而最小化总物流成本。

2.2 基本假设条件

(1)假设条件

1)已知每个设施在X轴方向上的长度与各个设施间的物流量，设施的形状为大小不等的矩形。

2)每个设施的物流交互点为该设施靠近过道边线的设施长度中点。

3)排列在通道两侧的设施数目已知，上下两行设施坐标均符合笛卡尔坐标系，最左侧起始点为坐标轴原点O。

4)相邻两个设施间没有间隙，且每层设施之间的通道宽度为0。

5)不同层的设施之间通过可移动升降货梯进行物流交互，假设货梯的宽度和长度均为0，仅考虑其升降高度，且升降高度h为已知量(h=10)。

6)各个设施之间的物料搬运长度采用曼哈顿距离计量。

(2)定义参数和变量

F为楼层集合，F={1,2}；

f为楼层编号，f∈F；

n为问题的规模；

Nf为f层设施的集合；

i,j,s为设施的编号；

cij为设施间的单位距离物流成本；

nf为布置在第f层的设施数目；

Rf,i为布置在第f层的第i个设施，f∈F；

dRf,i,Rf,j为f层的设施i与j之间的物流交互点在水平方向的距离；

li为设施在通道边线方向上的长度；

αij为二进制变量,如果设施i,j分配在同一行,且设施i被放置在设施j的左侧,则αij= 1，否则αij= 0。

2.3 考虑上下两层设施交互点位置距离约束条件

(1)基本DFCAP路径分析

基本DFCAP将货梯放在通道的最左侧，其两层设施之间的路径如图5所示。

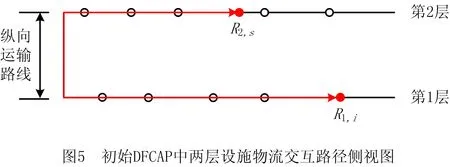
对于DFCAP，其设施的相对位置具有和传统单层CAP相同的性质，即均以坐标原点为起点，以X轴正方向沿通道两侧布置，且相邻两个设施之间无间隙，因此其第1层与第2层设施坐标可表示为：

设施i与设施s的物流交互距离dR1,iR2,s的约束条件为

(1)

(2)EDFCAP路径分析

EDFCAP采用移动升降货梯进行运输，其运输路径如图6所示。

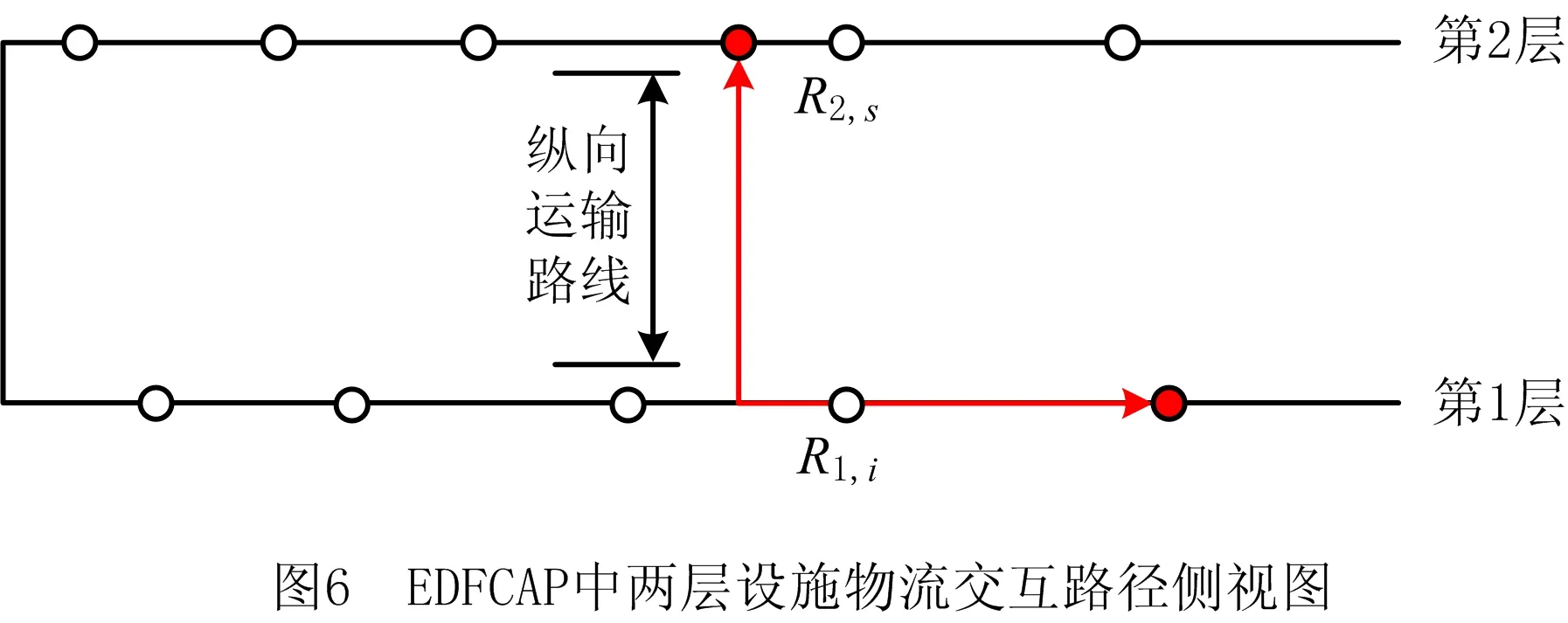
在EDFCAP中，任意两个设施之间的距离为dR1,iR2,s=h+|xR1,i-xR2,s|，因为在求解过程中，dR1,iR2,s均存在取值上限，所以将距离约束条件等价为dR1,iR2,s≥h+|xR1,i-xR2,s|，从而分解为如下线性约束条件：

(2)

(3)

2.4 基于移动货梯的双层过道布置问题数学模型

基于上述符号定义与问题描述，完整的EDFCAP的数学模型如下：

(4)

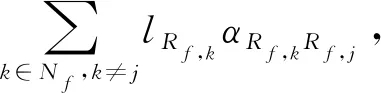
(5)

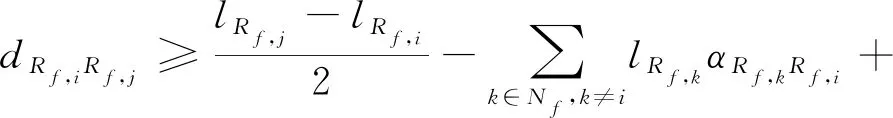
(6)

(7)

(8)

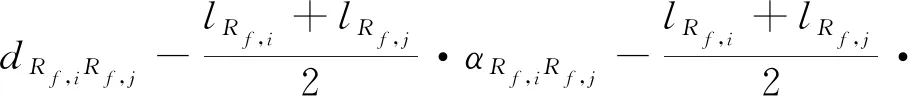
(9)

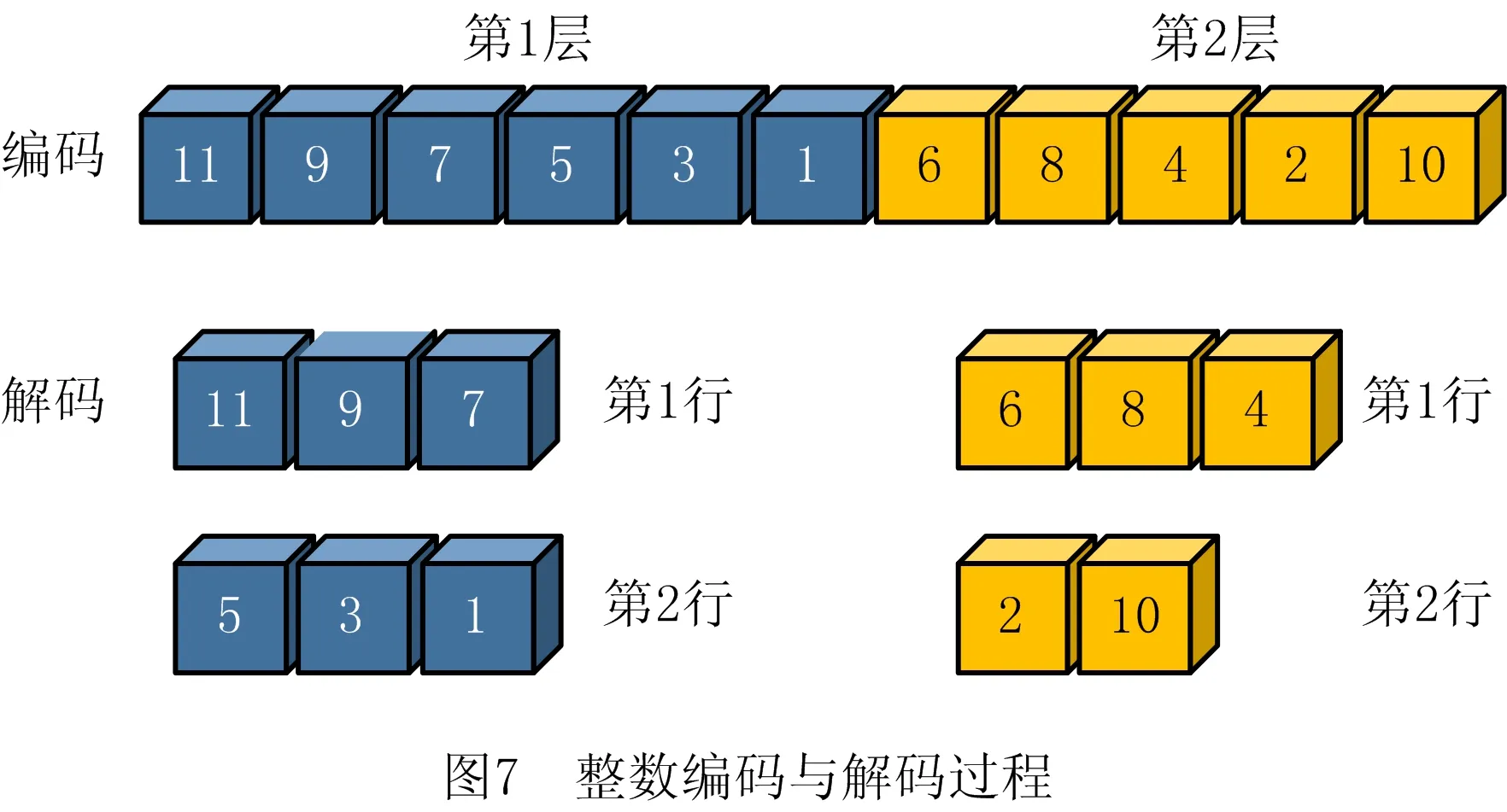
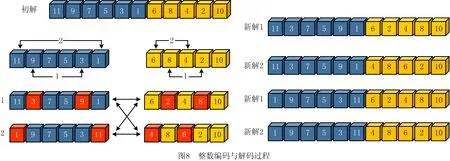
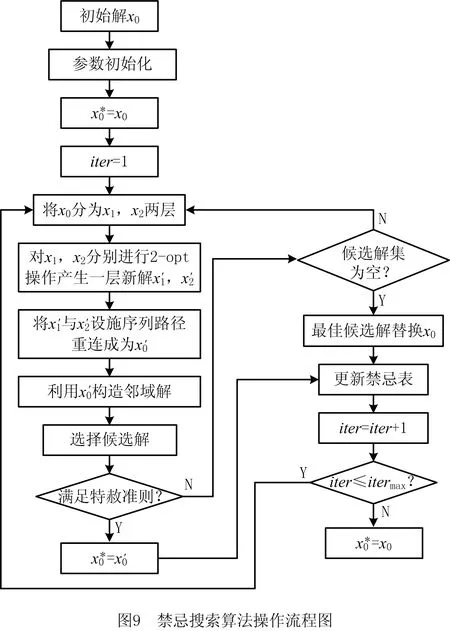
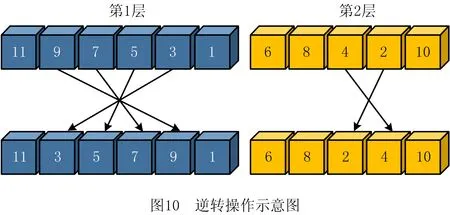
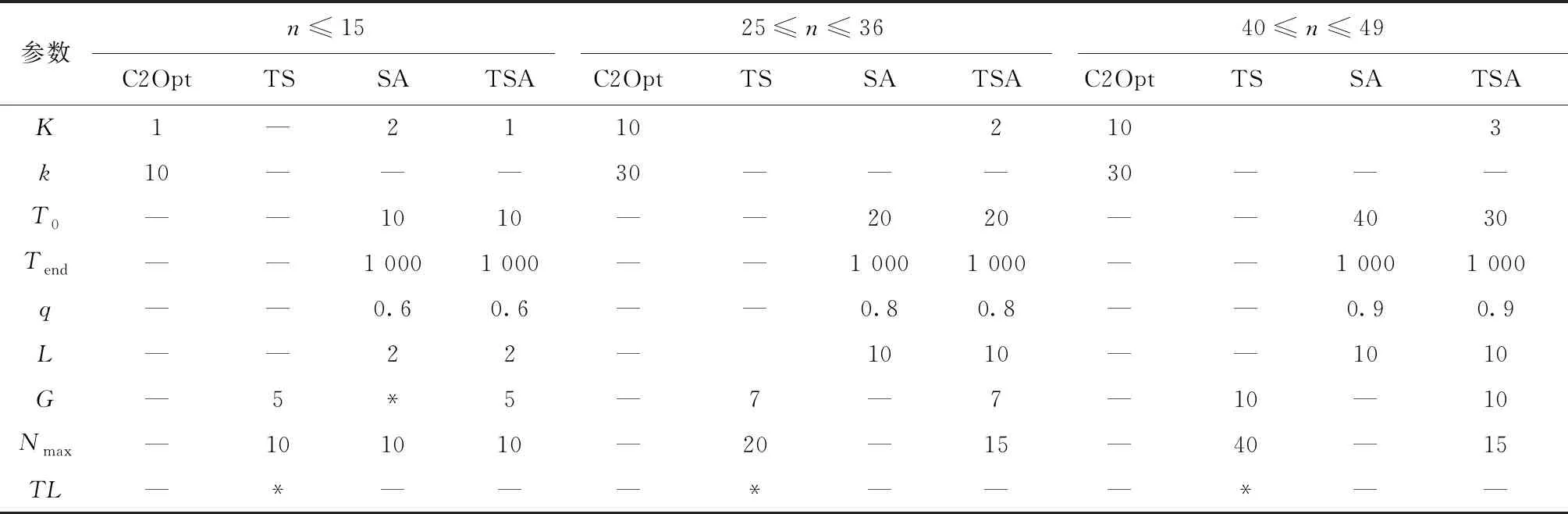
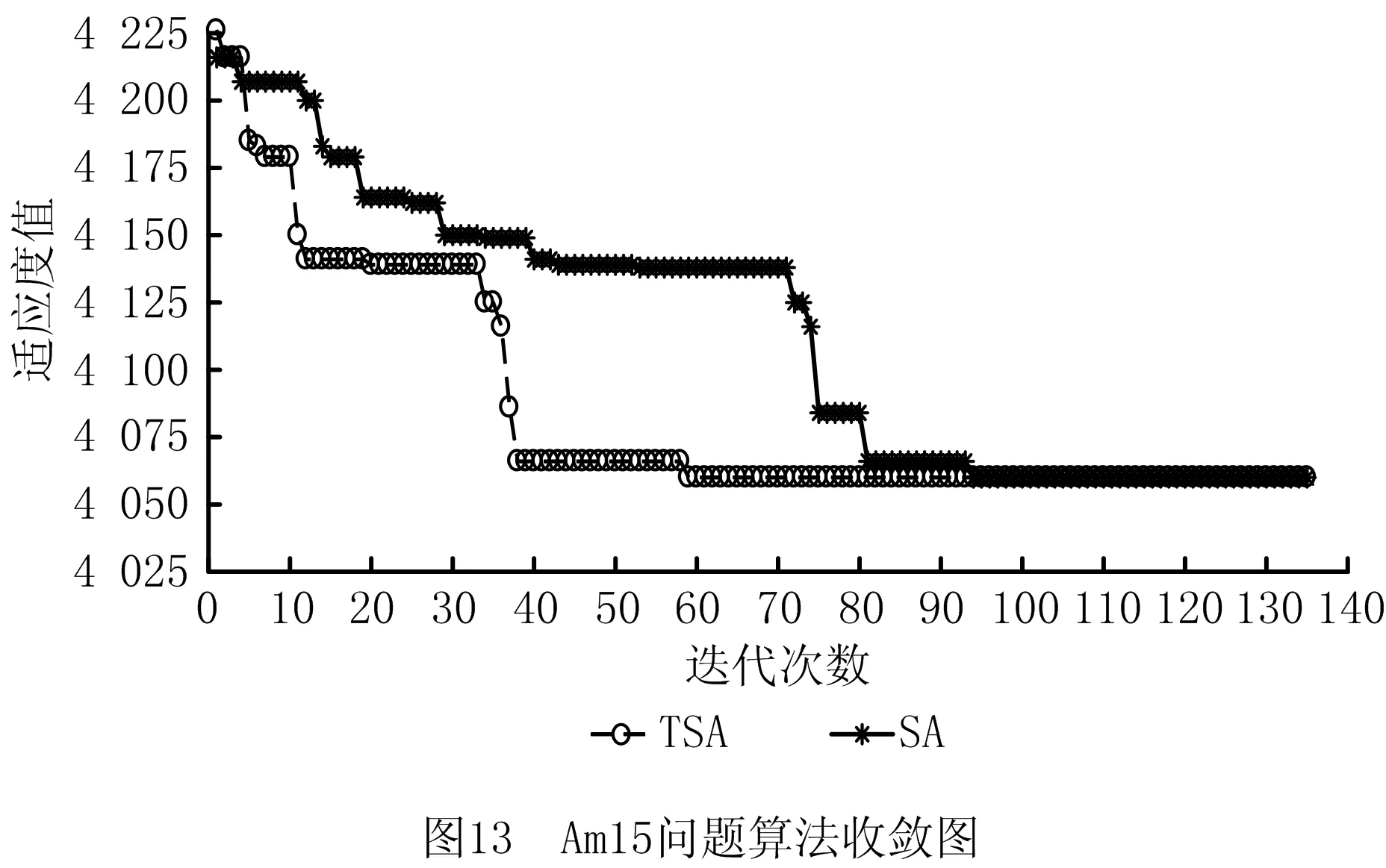
-αRf,iRf,j+αRf,iRf,k+αRf,jRf,k-αRf,jRf,i+
αRf,kRf,i+αRf,kRf,j≤1,
i,j,k∈Nf,i

(10)

-αRf,iRf,j+αRf,iRf,k-αRf,jRf,k+αRf,jRf,i-
αRf,kRf,i+αRf,kRf,j≤1,
i,j,k∈Nf,i

(11)

αRf,iRf,j+αRf,iRf,k+αRf,jRf,k+αRf,jRf,i+
αRf,kRf,i+αRf,kRf,j≥1,
i,j,k∈Nf,i

(12)

αRf,iRf,j∈{0,1},
1≤i,j≤n,i≠j,f∈F。

(13)

3 求解拓展双层过道布置问题的TSA

针对所提EDFCAP求解的复杂性，本文提出一种以SA算法为主体框架的融合2-Opt路径重连策略、记忆功能、禁忌搜索操作、inversion操作的TSA，以稳定地求得全局最优解。

3.1 编码、解码与2-opt路径重连策略

(1)编码与解码

针对EDFCAP的特征，本文采用实数编码设施序列，并对所编码的设施序列进行解码。以n= 11的经典算例为例，假定其中某一可行解的序列编码为[11 9 7 5 3 1 6 8 4 2 10]，若给定奇数号码的设施布置在第1层，偶数号码的设施布置在第2层，则第1层布置6个设施，第2行布置5个设施。每一层设施为整体设施序列的子序列，则解码的子序列可以划分为第1层第1行[11 9 7]与第1层第2行[5 3 1]、第2层第1行[6 8 4]与第2层第2行[2 10]，上述可行解的整数编码与解码过程如图7所示。

(2)2-Opt序列重连策略

为了更好地产生新的解序列，达到充分搜索邻域空间的目的，在原2-opt基础上对所产生的第1层新解和第2层新解进行序列重连，如图8所示。

相比于传统2-opt操作产生n个解序列，重连操作产生的解序列数为n2个，极大地增加了解的多样性；同时，在确定层与层之间布置的设施序编号不发生混乱的前提下，仅当新解的适应度值优于当前最优解时，输出新解。

3.2 记忆功能

传统SA算法收敛于全局最优解的关键在于Metropolis准则能以一定概率接受恶化解，使算法跳出局部最优，为避免在一定概率接受恶化解同时发生丢失当前最优解的情况，在SA算法中嵌入记忆功能，用于记录当前最优解。在进行模拟退火操作之初，记录初始解序列s0，并令xopt=s0，f(xopt)=f(s0)，在执行每一次Metropolis准则后，比较当前产生的可行解序列stemp对应的适应度值f(stemp)与历史最优解f(xopt)。若f(stemp)

3.3 禁忌搜索操作

采用具有局部搜索能力较强的全局迭代算法——TS算法改善SA算法的给定解，TS算法的操作步骤如图9所示。TS算法中：①邻域解的构成采用本文所提2-opt路径重连策略，并从所构成的邻域解中挑选候选解；②特赦准则为基于适应度值准则，即从当前邻域解中集中挑选候选解，并从候选解集中挑取最佳候选解，如果最佳候选解的适应度值优于历史最优值，达到best so far 状态，则藐视该解的禁忌特性，接受该解，并将其所对应适应度值作为禁忌对象加入禁忌表，同时更新禁忌表中其他禁忌对象的禁忌长度，作为TS算法中的核心策略，特赦准则增强了算法局部搜索性能，提高了获得全局最优解的概率；③算法中的禁忌对象为设施布置序列对应的适应度值；④兼顾求解时间和求解效率，经过多次求解测试，所提算法中TS算法的操作参数禁忌长度Tlength=round((n(n-1)/2)0.5)；⑤候选解集为邻域解的真子集。

3.4 逆转操作与终止准则

为了避免算法陷入局部最优，每次结束禁忌搜索操作后，记录当前最优解序列xbest，分别对输出的最优解对应序列的第1层和第2层进行inversion扰动(在每一层对应的序列中等概率随机选取两个不同的设施编码，并对两个设施编号中的所有设施进行逆转)，如图10所示。同交叉算子相比，inversion扰动可以使子代在跳出局部最优的同时最大程度地继承父代信息。本文以最外层迭代次数K为终止条件，K的取值根据问题求解规模n及最优值的稳定程度确定，设置i为混合SA算法完整流程次数的计数器，若i>k则算法终止，输出所记录的最优值f(xbest)和解序列xbest。

3.5 TSA步骤

TSA流程如图11所示。

步骤1初始化参数，包括初始温度T0、降温速率q、结束温度Tend、Metropolis链长L、最外层迭代次数K、禁忌搜索最大迭代次数Nmax。

步骤2随机产生初始解S0。

步骤3令i=1，k=1，count=1，若i≤K则执行步骤9，反之输出xbest，f(xbest)。

步骤4执行2-opt操作和Metropolies操作，同时开启记忆功能，令k=k+1。

步骤5若k≤L，则执行步骤4，否则执行步骤6。

步骤6结束循环时，输出记忆功能中记录的xopt，f(xopt)，若count= 1，f(x0) =f(xopt)，x0=xopt，则执行步骤8，否则执行步骤7。

步骤7若f(xopt)

步骤8降温T0=qT0，S0=x0。

步骤9若T0>Tend，则执行步骤4，否则输出x0，f(x0)。

步骤10执行禁忌搜索操作，并输出f(x0*)，x0*。

步骤11若f(x0*)

步骤12执行inversion扰动操作。

步骤13i=i+ 1。

步骤14若i≤K，则初始化温度T0，k=1，count=1并执行步骤4，否则输出xbest，f(xbest)。

4 实验结果与分析

为了验证所提EDFCAP数学模型的正确性，采用精确解优化器LINGO对上述模型进行精确求解，本文实验所采用的个人计算机硬件配置为 Intel(R) 酷睿 i5-8400、主频 2.8 GHz、内存 8 GB ，Windows10 操作系统。同时，为了验证所提TSA的求解性能，采用MATLABR2016b进行求解测试，随后将计算结果与文献[18]的启发式算法进行对比。为了避免问题参数的影响，选取与文献[18]相同的问题参数，问题参数与算法参数设置如表1和表2所示。实际设施布置中占地面积最小的情况一般为：每一层设施数目相差较小，且每层中两行设施数目相差较小。本文假设上下两层设施数目均为定值，即第1层均布置编号为奇数的设施，第2层均布置编号为偶数的设施。然而对于本文所构建的MIP模型，上下两层设施数目和奇偶设施序号设施布置并不局限于上述假设。

表1 问题参数设置(问题规模25≤n≤36)

表2 算法参数设置

4.1 EDFCAP模型验证

为了验证所提模型的正确性，根据所构建MIP数学模型的线性特性，应用LINGO优化器中的分支定界法对初始进行精确求解，测试算例S9，S9H，S10，S11，Am12，Am13，Am15，N25的运算时间Times分别为0，1，2，1.6，1，0.9，1.9，1.2，9.6，1 109.4(单位：s)。随着问题规模的增加，LINGO优化器求解过程中无法在较合理的时间内对大规模算例进行高效求解，因此为了给所提TSA求解结果提供参考，针对大于25规模的算例，将其运算时间设置在600 s，600 s后仍未求得结果则用“-”表示。对比表3的数据可知，针对小规模基准算例，TSA求得的最优解与精确算法求得的精确解相同，验证了所提模型与算法的正确性。

表3 LINGO精确解与TSA对EDFCAP的求解结果

4.2 TSA验证

为了说明TSA具有较好的求解性能与一定的普适性，结合DFCAP和CAP，选取9～49规模算例中的若干个算例进行验证，将TSA求解DFCAP和CAP的结果分别与C2Opt算法[18]求解DFCAP的结果、改进花授粉算法(Improved Discrete Flower Pollination Algorithm，IDFPA)[19]和改进的烟花算法(Improve Fireworks Algorithm，IFWA)[29]求解CAP的结果进行对比，如表4和表5所示。

表4 TSA和C2Opt算法求解DFCAP的结果对比

表5 算法TSA，IDFPA，IFWA求解CAP的结果对比

由表4可知，C2Opt和TSA两种算法的求解时间的增长均较平稳，且对于sko-49-05问题，TSA的求解结果优于C2Opt算法。由表5可知，对于小规模算例，3种算法求解出的目标值相等；对于较大规模算例，除sko-49-05问题外，TSA的目标值均可达到IDFPA和IFWA的目标值，且在sko-42-04，sko-49-03问题上求得的目标值更优，因此TSA具有较高的求解质量与普适性。

在验证基本DFCAP后，进一步说明所提算法的高效性。由于所提算法包括SA算法和TS算法，应用SA算法和TS算法分别求解所提EDFCAP，并与TSA进行对比，如表6所示。为了准确测试算法性能，算法均重复运行60次，将最优目标值记录在表中第3，5，7列。同时，为了更好地说明算法的稳定性，针对每个测试问题，统计3种算法的60次运算结果并计算标准差SD，如表6中的4，6，8列所示。

表6 各算法求解EDFCAP的结果对比

由表6可知，在相同参数下，针对9～15规模问题，3种算法均可得到最优解，但大于15规模后，TSA的求解质量明显优于TS算法和SA算法；为了直观地展现TSA的求解性能，将3种算法在不同规模下的求解标准差绘制成折线图，如图12所示。从图中可见，除AKv-80-05问题外，TSA求解问题的标准差指标均小于TS算法和SA算法，因此具有良好的求解稳定性。

根据计算结果，选定Am15问题算例并绘制如图13所示的迭代收敛图。为了对比明显，选用所含参数类别大致相同的SA算法做参照，将TSA和SA算法的参数设置为相同，由图可见两种算法的迭代收敛速度，当两种算法均可在有限次数内迭代到相对最优值时，TSA在59次时趋于平稳状态，SA算法则在94次时趋于稳定。因此TSA收敛速度较快，具有较强的搜索性能。