基于暂态电流差极值的电力变压器剩磁测量方法

任于展 武仕朴 汪友华 刘成成 火彩玲

基于暂态电流差极值的电力变压器剩磁测量方法

任于展1,2武仕朴1,2汪友华1,2刘成成1,2火彩玲1,2

（1. 省部共建电工装备可靠性与智能化国家重点实验室（河北工业大学） 天津 300130 2. 河北省电磁场与电器可靠性重点实验室（河北工业大学） 天津 300130）

电力变压器在空载合闸过程中产生的励磁涌流会对电网及设备产生诸多不利影响。为有效削弱铁心中的剩磁以降低励磁涌流出现的概率，准确测量铁心内剩磁的大小及方向十分必要。基于磁性材料的电磁暂态特性，该文提出一种外施直流电压的剩磁测量方法，剩磁导致绕组中施加正、反向电压下的暂态电流波形不同，结合场路分析，建立了剩磁与暂态电流差极值之间的关系。为提高剩磁测量的准确性，对待测方形铁心进行建模和分析，优选了一组合适的测试电路参数，并依据有限元计算结果拟合得到铁心中剩磁与暂态电流差极值关系的经验公式，为变压器铁心剩磁的定量检测奠定基础。最后搭建测量平台，对待测铁心进行实验研究，测量结果验证了所提方法的可行性和准确性。

电力变压器 励磁涌流 剩磁 场路分析 暂态电流差

0 引言

大型电力变压器在检测试验和在线运行分闸之后，由于铁磁性材料的磁滞特性，铁心中会残留一定的剩余磁通。变压器空载合闸时，剩磁的存在会加速铁心半周饱和，在一定电源电压作用下，可产生幅值相当于6～8倍额定电流的励磁涌流[1-5]。励磁涌流容易导致继电保护误动作、电网电压下降、变压器绕组应力增大与损坏敏感电力电子器件等不良影响，危及公共电网的安全运行[6-7]。

选相合闸技术通过控制断路器的合闸时间（即合闸时系统电压的初相角），在铁心中的预感应磁通与剩磁相等时投入变压器，可避免铁心饱和，从而有效地抑制励磁涌流。该技术比基于合闸电阻与并联电容器的限制涌流措施更可靠、更经济[8-10]。但这要求空载合闸前准确地预估铁心内剩磁的大小及方向，因此剩磁的准确测量对大型电力变压器保护具有重要参考意义。

近年来，国内外学者相继提出了一些剩磁的测量方法。1984年国际大电网会议（International Council on Large Electric Systems）通过对超过500台运行后的变压器调查，结果发现铁心内剩磁大多为0.7倍的额定磁通密度[11]。文献[12]对试验运行后的变压器剩磁进行分析，发现剩磁一般在20%～70%的饱和磁通密度范围内。剩磁的经验估算方法可为变压器出厂前的试验提供参考，但实际应用误差大且无法判断剩磁的方向。文献[13]采用磁通门传感器，通过测量变压器铁心周围漏磁场从而实现剩磁测量，但该方法的准确性受传感器灵敏度和安装位置的影响，且仅适用于无油箱变压器，因此适用范围并不广泛。文献[14]经分析得到励磁涌流峰值与剩磁之间的关系，但该方法仅能在通电合闸后通过励磁涌流第一峰值反推剩磁大小，并不能在合闸前对铁心内剩磁数值进行计算，因此该方法无法帮助变压器合闸时抑制励磁涌流的产生。基于法拉第电磁感应定律的电压积分法是目前最为常用的剩磁测量手段。文献[15-18]提出通过采集变压器分闸前一段时间内的电压数据进行积分，从而确定剩磁。但采集的电压信号难免存在噪声、漂移等，且单纯的积分方法会无限地累计这种误差，导致测量结果准确性低，并且由于存在一种磁粘性的现象[19]，铁心内磁畴结构即使在没有施加外部磁场情况下也可能会随时间发生变化。因此如果变压器分合闸的间隔时间过长，铁心内的剩磁值将会发生改变，使得该方法的测量结果失去参考意义。

针对现有研究存在的问题，本文从电力变压器铁心剩磁产生机理出发，依据铁心材料电磁暂态特性建立可测量参数与剩磁之间的关系，提出了一种基于暂态电流差极值特征的剩磁测量方法。首先依据变压器等效电路模型，推导得到暂态电流差极值与剩磁之间的关系；然后以不同剩磁下铁心材料的磁特性曲线为基础，利用有限元软件对待测变压器铁心进行建模和计算，通过仿真分析确定相关测试激励的参数，并依据计算结果拟合得到剩磁与暂态电流差极值参数之间的经验公式；最后搭建方形铁心的实验测量平台，验证提出测量方法的可行性。实验结果表明，该方法对变压器铁心内剩磁具有较高的测量精度。

1 剩磁测量原理

1.1 剩磁产生原理

铁心通常采用铁磁材料叠压制成，为变压器提供磁回路[20]。目前在铁磁材料的磁特性研究中，磁畴理论较为成熟，通过对磁畴的研究，可从微观上阐明铁磁材料的磁化机理。磁性材料的磁化过程整体分为三个阶段：①在无外部磁场作用下，磁畴排列杂乱无序，产生的磁效应相互抵消，整个铁磁材料对外呈现磁中性状态；②在外部磁场作用下，各磁畴发生定向的磁畴转动和畴壁位移，改变原有磁畴结构，磁畴排列逐渐进入有序化；③当去除外部磁场时，由于铁磁材料特有的磁滞现象，磁通密度与磁场强度相差一个相位，铁磁材料不能恢复到磁中性状态，而是保持在一个稳定的磁化强度，即剩磁[18]。磁化过程示意图如图1所示。

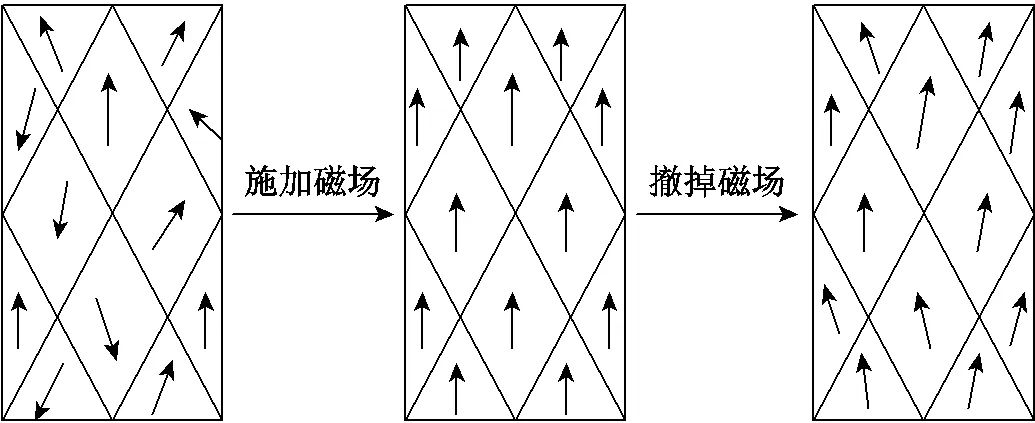
图1 磁畴磁化过程示意图

磁滞现象是铁磁性材料的独特性能，这是因为磁化过程中磁畴转动和畴壁位移使得能量发生转换，产生了磁滞损耗，因此磁化过程具有不可逆性。另一方面，铁心中剩磁的产生意味着先前磁化过程中施加的磁场足够大，磁畴之间的耦合强度发生了变化，铁心经历了不可逆磁畴壁位移的阶段，即有巴克豪生跳跃发生。剩磁是判断磁性材料的关键性能参数，是不可逆磁化的重要标志[2]。

大型电力变压器长期运行时，铁心在交变磁场中反复磁化。由于实际运行工况复杂，且受现场设备条件的制约，难以实时准确测量具有封闭磁路结构的铁心，记录内部磁通密度的变化。

1.2 剩磁对励磁电感的影响

铁磁性材料在外磁场的作用下产生磁通密度。随着外磁场强度的增加，磁通密度呈非线性变化。对于铁磁性材料磁化过程的状态变化可以由瞬态过程中微分磁导率rd反映[21]，将其定义为磁通密度增量d与磁场强度增量d之比，即

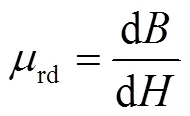
在建立磁场的过程中，实际变压器绕组相当于一个带铁心的线圈，瞬时的励磁电感m反映励磁作用的能力，其计算公式为

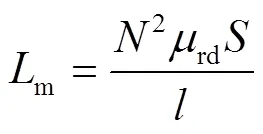
式中，为线圈匝数；为铁心的截面积；为铁心有效磁路长度。可以看出，变压器铁心励磁电感与铁心内磁通密度有关。剩磁的存在会导致铁心微分磁导率发生变化，与励磁电感特性有关的电路实验将会受到影响[22-23]。采用场路耦合的方法，将具有封闭磁路结构难以测量的磁场问题，转换成关于励磁电感便于测量的电路问题。

1.3 剩磁测量方法理论分析

本文选取方形变压器铁心作为研究对象。由于变压器铁心的磁导率远高于空气间隙，因而忽略漏磁因素，且低频情况下容抗远小于感抗，这里不考虑电容的影响，可以得到实验测量时的等效电路如图2所示。

图2 实验测量等效电路

当一次绕组施加直流电压激励后，基于变压器等效电路和基尔霍夫电压定律，流经一次绕组的瞬时电流()满足

式中，s为外部串联电阻；w为变压器一次绕组电阻；m为具有非线性特性的励磁电感。

从图2可知，变压器的等效电路可近似为一阶RL电路。绕组中电流达到稳态前会经历一个暂态过渡过程，其暂态电流变化速率受时间常数影响，表达式为

式中，为包含回路中s和w的总电阻。根据式（3）和式（4），可得暂态电流表达式为

式中，s为电路达到稳态时的电流值。

为了确定铁心内初始剩磁方向，对一次绕组施加正、反向的直流电压激励。在同一剩磁下，外施磁场强度的方向不同时，铁磁材料的微分磁导率是不一样的，因此暂态电流时间常数也不同。根据式（5）可得

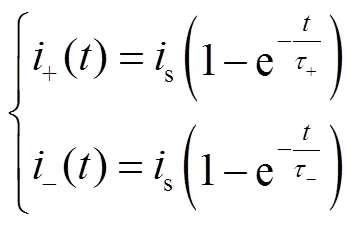
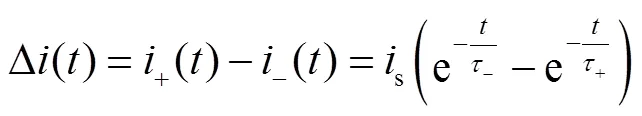
当时间＞0时，暂态电流差值波形Δ()如图3所示。

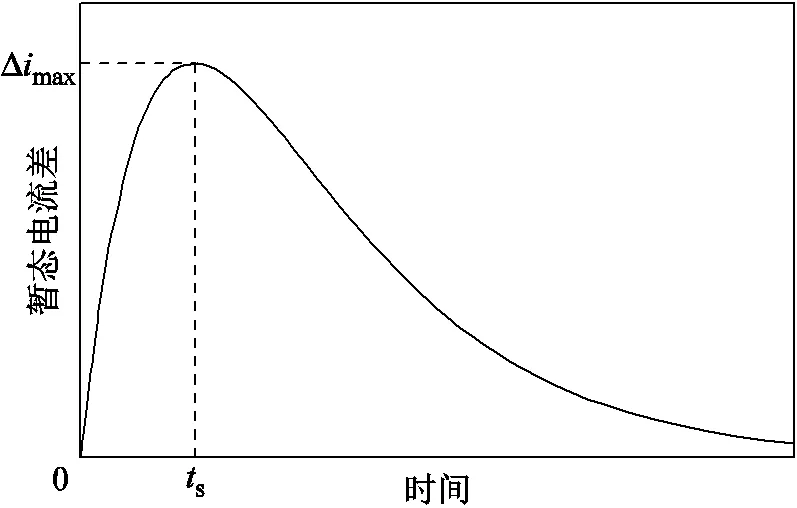
图3 暂态电流差值波形

波形仅含一个波峰，因而其函数存在一个固定极值。为求取其极值，对Δ()进行求导。当导函数为式（8）时，方程解即为函数极值时间s。

联立式（7）和式（8），得到暂态电流差极值时间s与极值大小Δmax分别为

综上所述，对于未知剩磁的变压器铁心，施加幅值相同极性相反的直流电压激励，铁心内剩磁将会影响暂态电流差的极值参数，为利用波形特征的识别提供了依据。由于暂态电流差值波形呈现单波峰特点，具有便于准确识别的特性，因此本文通过可测量参数暂态电流差极值建立与剩磁之间的关系，实现对具有封闭磁路结构铁心中的剩磁测量。

其次，测量实际剩磁之前，铁心内剩磁方向是未知的，因此一次绕组先后施加正、反向直流电压。施加正向激励时的暂态电流变化速率要快于施加反向激励时的暂态电流变化速率[24]，所以同一对应时刻下正向暂态电流值大于反向暂态电流值。通过暂态电流波形上升速率及计算得到的暂态电流差Δ()符号可以快速判断铁心内剩磁方向。

2 仿真计算分析

为了研究不同剩磁下变压器铁心的电磁暂态特性，本文按照电力变压器铁心的设计标准和叠装工艺，设计并制作了一台产品级的变压器方形铁心模型。铁心材料选用宝钢公司（Baosteel）生产的B30P105冷轧取向电工钢，铁心模型参数见表1。

表1 铁心模型参数

Tab.1 Parameters of the core model

仿真中铁心材料的磁特性曲线由实验平台直接测量，由于所提剩磁测量方法施加的是直流电压，因此按图4所示测量步骤测量得到不同剩磁下铁心材料的直流磁化曲线。通过这种测量方法得到的直流磁化曲线能够精确反映不同剩磁下铁心材料的磁特性，并且针对同种铁心材料的变压器仅需测量一次。有限元软件中铁心建模如图5所示。

图4 不同剩磁下铁心材料的直流磁化曲线测量步骤

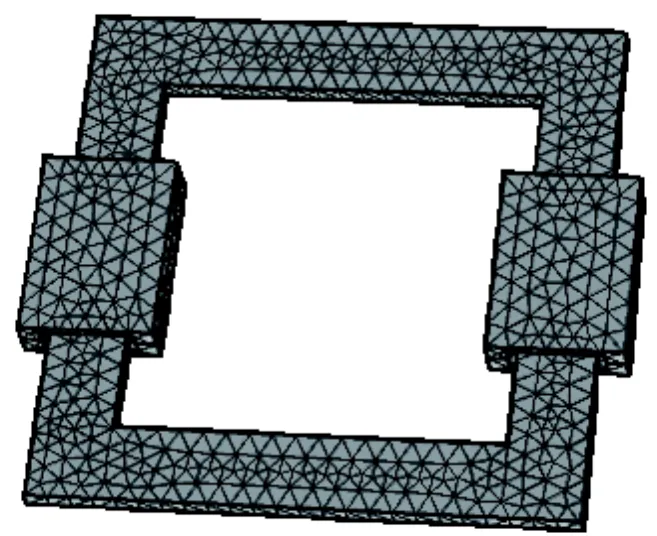
图5 方形铁心有限元模型

2.1 测试电路参数分析

为保证所提剩磁测量方法结果的准确性，进行暂态仿真分析前，需确定外部电路参数及施加在绕组上的直流电压幅值。

2.1.1 外部串联电阻的参数分析

本文结合数据采集卡和LabVIEW搭建了一维磁特性实验平台，测量得到无剩磁下铁心材料的直流磁化曲线如图6所示。

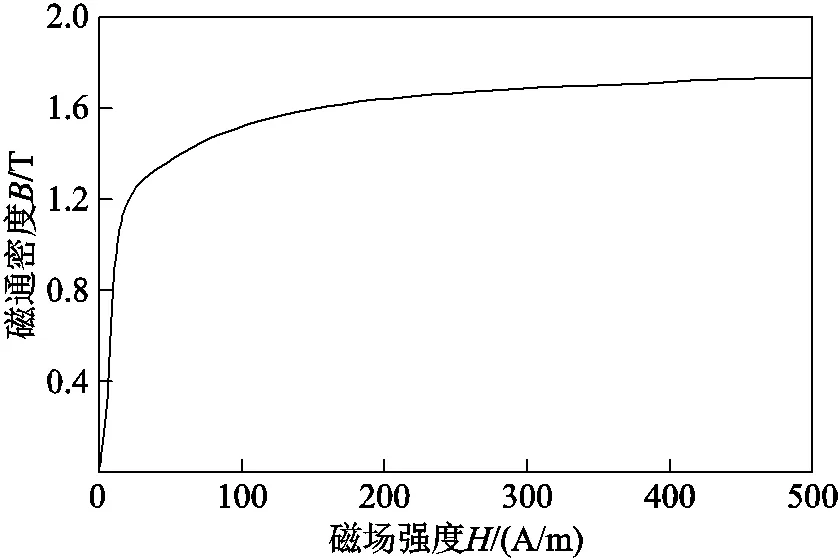
图6 铁心材料直流磁化曲线

由式（1）可知，铁磁材料的微分磁导率rd与磁通密度有密切的联系。对测量得到的直流磁化曲线进行一阶微分求导，可绘制出rd与的关系如图7所示。可以看出铁心材料的rd随的变化规律呈先上升后下降的趋势，且存在唯一最大的微分磁导率max。在初始磁化阶段，rd迅速上升并达到max，然后rd逐渐下降。

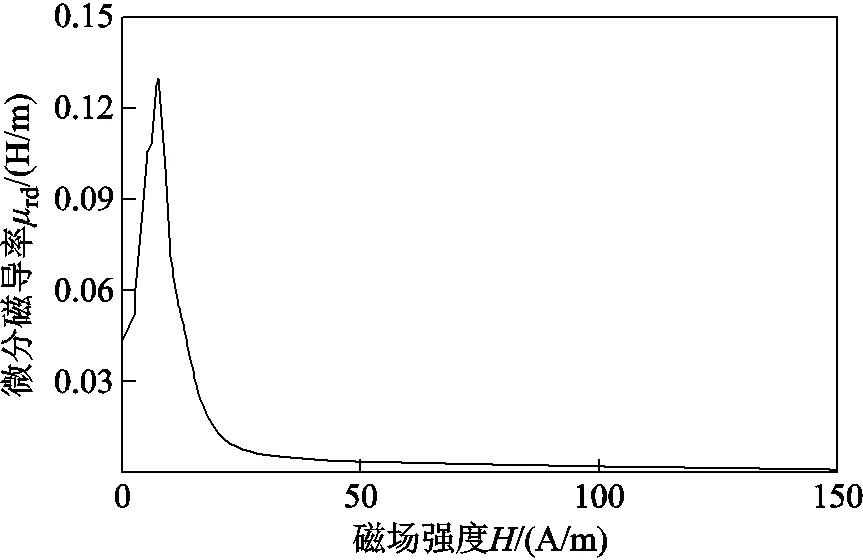
图7 铁心材料微分磁导率与磁场强度的关系曲线

对待测铁心进行仿真分析时，一次匝数，铁心有效磁路长度，有效横截面积均不会发生改变，因此铁心励磁电感m主要受rd影响。虽然有初始剩磁情况下rd变化规律与没有剩磁情况有所不同，但可以借助无剩磁时铁心材料直流磁化曲线对给定结构下的铁心进行励磁电感值的范围估算。由图7及式（2）推算得到待测方形铁心的励磁电感值在0～0.271H范围内。

变压器二次绕组始终处于空载状态，因而待测变压器铁心结构可近似为一阶RL电路，测量电路中的总电阻由外部串联电阻s及一次绕组电阻w组成。当绕组材料和结构确定时，其电阻w为定值。外部串联电阻s起调节暂态过程时间常数和限制电流保护电路的作用。本文依据rd推算得到待测铁心励磁电感范围，为调节时间常数选取s分别为1Ω、4Ω、20Ω进行仿真分析。

一次绕组施加产生相同测量磁通密度t的直流电压激励，即施加直流电压后绕组中稳态电流值均为30mA。不同串联电阻下暂态电流差仿真波形如图8所示。改变外部串联电阻s，暂态过程发生明显变化。当s为20Ω时，电流暂态过程时间过短，难以体现和捕捉暂态过程中剩磁导致的电流变化；当s为1Ω时，电流暂态过程时间过长，逐渐变化的电流将对原有剩磁产生影响，降低测量精度；当s为4Ω时，电流暂态过程时间约在200ms以内，易于获取并处理电流波形。为提高测量结果的准确性，针对最大励磁电感为0.271H的待测铁心，对比分析得到4Ω的外部串联电阻可以满足要求。

图8 不同串联电阻Rs下暂态电流差仿真波形

2.1.2 电压激励的参数分析

剩磁测量采用的原则是基本不改变铁心内原有剩磁大小且便于获得电流差值，否则测量结果准确性将会受到影响。因此施加在绕组上的直流电压激励幅值应远小于变压器的额定工作电压，使得产生的外部磁场无法克服矫顽力而导致剩余磁通密度方向不变，铁心内磁畴运动以发生可逆磁化过程为主，且应充分体现出受变压器铁心内初始剩磁的影响。

针对饱和磁通密度理论可以达到1.8T的B30P105硅钢材料，推算该材料铁心内剩磁一般为0.4～1.2T[12]。由于铁磁性材料固有的磁滞特性，为保证施加的测试激励对不同剩磁下铁心影响均在允许范围内，因而理论选取的测量磁通密度t不应超过最小剩磁值的10%，本文选取t分别为5mT、15mT、25mT的情况进行仿真分析。

首先，依据图6的直流磁化曲线可以确定产生t对应的外施场强t，根据安培环路定律可得

由式（11）将外部施加的磁场强度t转换为励磁电流t，t为电路达到稳态时流经绕组的电流值，此时电感已不起作用，基于等效电路和基尔霍夫电压定律可得

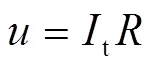
根据式（11）和式（12），能够得到产生的测量磁通密度对应施加在一次绕组上的直流电压幅值。

铁心内剩磁相同时，施加不同测量磁通密度下的暂态电流波形如图9所示。可以看出，当t为5mT时，正、负向暂态电流波形基本完全重合，难以区分，出现这种原因可能是因为测量磁通密度太小，发生的可逆磁化过程无法受到初始剩磁的牵制作用。当t为15mT时，不同激励方向下的暂态电流变化速率呈现出差异，可借此快速准确地判断出铁心内剩磁方向。但是暂态电流差值范围在3mA以内，不同剩磁下的差值变化可能会更小，这对现场测量装置精度和抗电磁干扰要求很高，实际难以准确测量和采集暂态电流信号，从而会影响后续剩磁大小的确定。当t为25mT时，暂态电流波形差异明显，且易于信号的采集和计算。

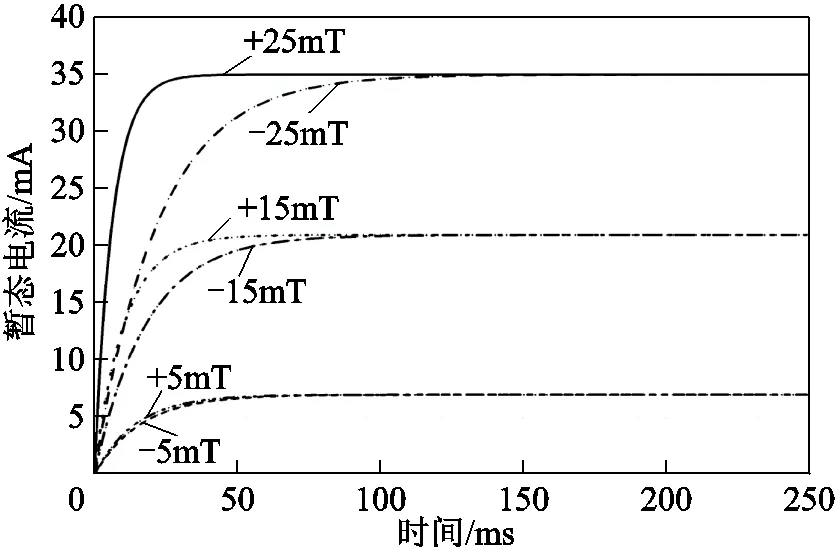
图9 不同测量磁通密度Bt下暂态电流仿真波形

其次，由于含剩磁情况下的铁心正反向磁化能力不同，施加测试激励结束后，磁性材料固有的磁滞特性导致铁心内剩余磁通密度将会发生变化。r为铁心内初始剩余磁通密度，r1为施加测试激励后铁心稳态时的剩余磁通密度。当t为25mT时，铁心内剩余磁通密度变化见表2。可以看出，铁心内剩余磁通密度变化率Δ最大不超过8.51%，若选择的t增大，Δ将会超出10%，影响剩磁测量结果的准确性。因此依据分析选取幅值为150mV的直流电压，测量结果能够满足工程上的要求。

表2 铁心内剩余磁通密度变化

Tab.2 The change of residual flux density in the core

该方法同样适用于其他铁心材料和结构的实际变压器，仅需要对其进行相同的分析步骤即可重新确定对应的串联电阻和直流电压幅值。

2.2 剩磁与暂态电流差极值参数的关系

为确保结果具有代表性和可重复性，针对不同剩磁下的铁心，一次绕组先后施加幅值为150mV的正、反向直流电压，暂态电流差的有限元仿真结果如图10所示。

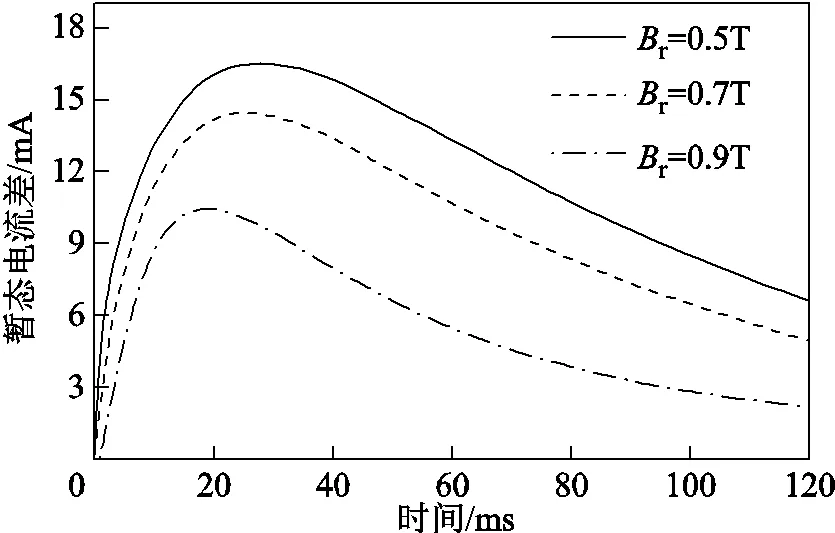
图10 不同剩余磁通密度下暂态电流差仿真波形

可以明显看出，暂态电流差值波形随剩磁改变发生明显变化，通过分析波形可以得到铁心内剩磁大小。本文研究铁心内剩磁对暂态电流差值波形的影响，并通过暂态电流差极值Δmax和极值时间s参数实现对剩磁值的定量分析。

暂态电流差极值参数随剩余磁通密度变化曲线如图11所示，可以看出暂态电流差极值点参数s和Δmax随剩磁的增加都呈下降趋势，且与剩磁都为单值函数关系，因而可以实现对铁心内剩磁值的定量分析。但从图11a和图11b对比可以看出，极值时间s对铁心内剩磁的变化更为敏感，易于后续信号的测量和处理，因此本文选取暂态电流差极值时间s为自变量，剩余磁通密度r为因变量，进行经验公式的拟合。

图11 暂态电流差极值参数随剩余磁通密度变化曲线

基于最小二乘法原理，对有限元计算得到的离散点选用不同拟合方式并得到相应拟合函数。剩余磁通密度与暂态电流差极值时间s拟合曲线如图12所示。从图12可以看出，选用线性拟合时，离散点并不能更多地落在拟合曲线上，其难以准确反映二者之间的关系。使用指数函数进行拟合时，可以看出拟合效果较好，其残差二次方和仅为0.002 69，证明指数拟合可以较好地反映暂态电流差极值时间s与剩余磁通密度r之间的函数关系。拟合得到的经验公式表达式为

3 实验测量与结果分析

3.1 实验测量平台

为了验证所提方法的可行性和准确性，本文按照图13所示剩磁实验测量平台示意图设计并搭建如图14所示的实验测量平台。在实验平台中，采用信号发生器（WF1974）生成输入激励信号，并通过功率放大器施加在50匝的一次绕组上，使用示波器（DSOX6004A）和电流探头（N2782B）测量并存储暂态电流信号数据，二次绕组始终保持空载状态，仅在实验测量过程中连接磁通计（Flux-meter480）以观察并记录铁心内磁通密度的变化。

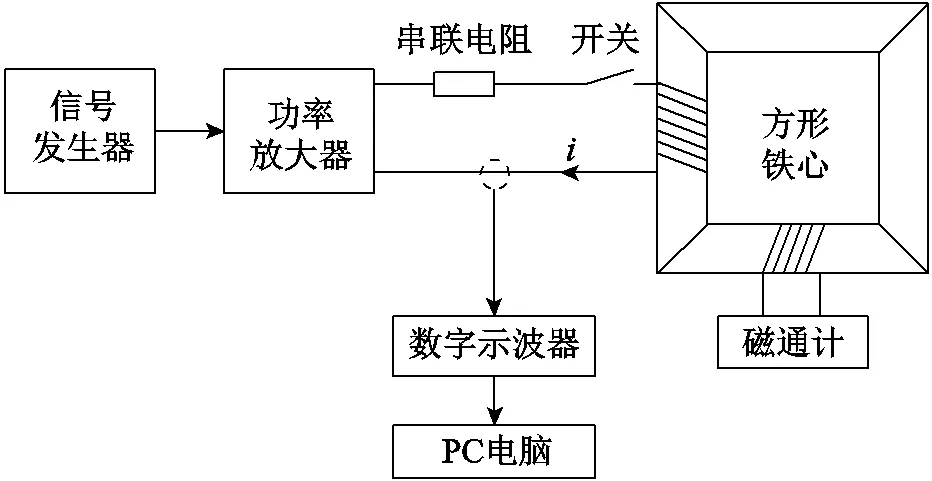
图13 剩磁实验测量平台示意图

图14 实验测量平台

3.2 变压器铁心剩磁预设方法

变压器铁心中剩磁的准确预设是测量实验的关键。为了避免铁心中由未知因素产生对实验的误差干扰，同时使每次测量不受上次实验的影响，提高实验结果的准确性和可靠性。每次预设剩磁实验之前，通过两次交流退磁处理对铁心进行彻底消磁后，再进行剩磁预设。

采用直流激励的方法在变压器铁心中产生剩磁，对一次绕组施加不同幅值的直流电压并缓慢撤掉，当铁心内磁通密度稳定不再变化时，即为预设剩磁r。实验过程中通过配合磁通计的读数实现对铁心剩磁大小的精准预设。

3.3 剩磁测量结果与分析

采用电流探头与数字示波器结合的方式，对实验过程中暂态电流波形进行数据采集，并将先后采集到的两组暂态电流数据直接相减即可得到暂态电流差值波形。

铁心中剩磁r为0.79T时，经采集和处理得到的暂态电流差值波形如图15所示。可以看出，测量结果与仿真结果吻合度较高，但由于施加的电压激励幅值较小，采集到的暂态电流信号中噪声含量较大。为精准提取暂态电流差极值时间s，就要求对采集到的暂态电流进行有针对性的信号后处理。

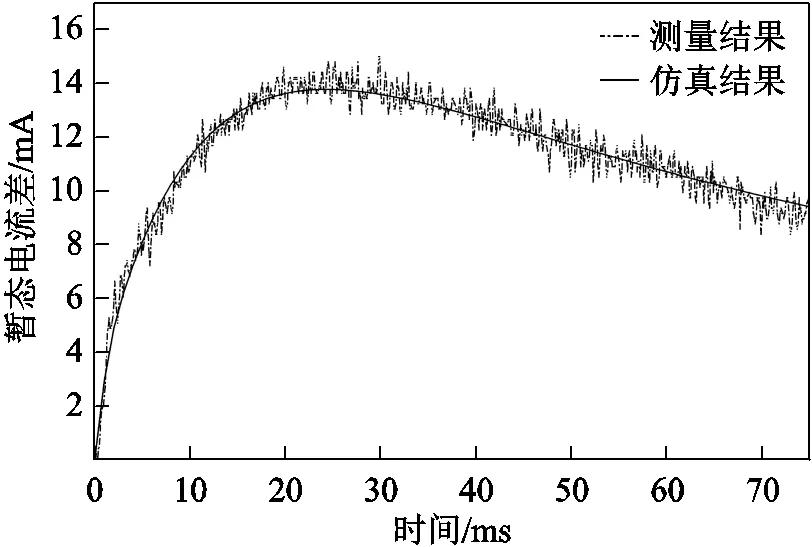
图15 暂态电流差仿真与实验波形

对方形铁心预设不同剩磁后进行相同的测量实验，将采集的数据进行低通滤波和平滑处理[25]后提取暂态电流差极值时间s，并利用拟合得到的经验公式估算出铁心内剩余磁通密度。

将铁心内剩磁的实际值与估算值进行对比，如图16所示。可见实际值与估算值基本一致，最大误差出现在s为27.09ms时，实际值高于估算值约5.4%。考虑到测量数据的采集、信号的后处理以及铁心材料实际参数与仿真模型的误差，认为上述测量误差在可以接受的允许范围内。此外，估算值与剩磁值随剩磁变化的趋势一致，因此认为本文所提测量方法是可靠的。

图16 实际剩磁值与估算剩磁值对比

4 结论

本文依据铁心材料的电磁暂态特性，提出了一种基于暂态电流差极值的电力变压器剩磁测量方法。通过有限元的建模和仿真分析，研究了铁心内剩磁和电路参数对暂态电流波形的影响，为剩磁测量提供了理论参考。最后搭建方形铁心的实验测量平台，测量结果表明通过暂态电流差极值能够定量检测铁心内剩余磁通密度，且测量精度较高。本文所提剩磁测量方法具有以下几点优势：

1）选取直流电压小信号作为测试激励，便于在实际现场中获得。

2）测量过程前后，测试激励对铁心内剩磁影响较小同时不对变压器做任何要求。

3）避免了铁心磁黏性现象导致的误差干扰，有利于提高剩磁测量精度。

4）测量波形局限在较低的频带，对测量设备要求不高，便于应用推广。

在后续工作中，将对不同类型的变压器铁心结构进行研究分析，并依据本文的研究结论提高选相合闸技术准确度和退磁方式的改进，削弱励磁涌流的影响。

[1] 王小君, 毕成杰, 金程, 等. 电气化铁路不停电过分相电磁暂态及抑制措施研究[J]. 电工技术学报, 2021, 36(1): 191-202.

Wang Xiaojun, Bi Chengjie, Jin Cheng, et al. Research on electromagnetic transient and suppression measures for passing neutral section without power interruption of electrified railway[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 191-202.

[2] 戈文祺, 汪友华, 陈学广, 等. 电力变压器铁心剩磁的测量与削弱方法[J]. 电工技术学报, 2015, 30(16): 10-16.

Ge Wenqi, Wang Youhua, Chen Xueguang, et al. Method to measure and weaken the residual flux of the power transformer core[J]. Transactions of China Electrotechnical Society, 2015, 30(16): 10-16.

[3] 曹文斌, 尹项根, 张哲, 等. 变压器三角绕组环流助增作用分析及其工程求取方法[J]. 电工技术学报, 2020, 35(15): 3161-3172.

Cao Wenbin, Yin Xianggen, Zhang Zhe, et al. Analysis of the helping effect and engineering calculation method for transformer circulating current in delta winding[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3161-3172.

[4] 赵永彬, 陆于平. 基于磁通对称特性的变压器励磁涌流判别新算法[J]. 电工技术学报, 2007, 22(12): 66-71.

Zhao Yongbin, Lu Yuping. A new algorithm based on flux symmetry character for judging transformer inrush current[J]. Transactions of China Electrotechnical Society, 2007, 22(12): 66-71.

[5] 翁汉琍, 刘雷, 林湘宁, 等. 涌流引起换流变压器零序过电流保护误动的机理分析及对策[J]. 电力系统自动化, 2019, 43(9): 171-178.

Weng Hanlin, Liu Lei, Lin Xiangning, et al. Mechanism and countermeasures of mal-operation of converter transformer zero-sequence overcurrent protection caused by inrush currents[J]. Automation of Electric Power Systems, 2019, 43(9): 171-178.

[6] 刘鹏辉, 黄纯, 石雁祥, 等. 配电线路励磁涌流自适应闭锁方案[J]. 电工技术学报, 2019, 34(11): 2395-2404.

Liu Penghui, Huang Chun, Shi Yanxiang, et al. An adaptive blocking scheme for magnetizing inrush current in distribution lines[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2395-2404.

[7] 李春艳, 周念成, 王强钢, 等. 基于软启动的变压器励磁涌流抑制方法[J]. 电工技术学报, 2020, 35(17): 3640-3651.

Li Chunyan, Zhou Niancheng, Wang Qianggang, et al. A method to eliminate transformer inrush currents using soft-starter-based controlled energization[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3640-3651.

[8] 陈川江, 方春恩, 曾俊龙, 等. 计及剩磁的空载变压器选相合闸研究[J]. 电力系统保护与控制, 2018, 46(16): 82-88.

Chen Chuanjiang, Fang Chunen, Zeng Junlong, et al. Research on unloaded transformer controlled switching considering residual flux[J]. Power System Protection and Control, 2018, 46(16): 82-88.

[9] 陈川江, 方春恩, 李伟, 等. 计及剩磁的中性点不接地变压器选相合闸仿真与实验[J]. 高电压技术, 2019, 45(11): 3521-3528.

Chen Chuanjiang, Fang Chunen, Li Wei, et al. Simulation and experiment of controlled switching for isolated neutral transformer considering residual flux[J]. High Voltage Engineering, 2019, 45(11): 3521-3528.

[10] 张瑞, 甘战, 张鹏, 等. 换流变压器空载励磁涌流选相关合控制策略[J]. 电力系统保护与控制, 2019, 47(15): 69-77.

Zhang Rui, Gan Zhan, Zhang Peng, et al. Controlled switching strategies to eliminate the inrush current of converter transformer[J]. Power System Protection and Control, 2019, 47(15): 69-77.

[11] Colombo E, Santagostino G. Results of the enquiries on actual network conditions when switching magnetizing and small inductive currents and on transformer and shunt reactor saturation characteristics[J]. Electra, 1984, 94: 35-53.

[12] Wu Yunfei, Hu Huiran, Luo Wei, et al. Research on no-load test of 1000kV ultra-high voltage transformer[C]//2011 Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 2011: 1-6.

[13] Cavallera D, Oiring V, Coulomb J L, et al. A new method to evaluate residual flux thanks to leakage flux, application to a transformer[J]. IEEE Transactions on Magnetics, 2014, 50(2): 1005-1008.

[14] 李勇, 金明亮, 李海涛, 等. 电力变压器剩磁测量方法研究[J]. 电力系统保护与控制, 2019, 47(15): 102-107.

Li Yong, Jin Mingliang, Li Haitao, et al. Study on measurement method of remanence of power transformer[J]. Power System Protection and Control, 2019, 47(15): 102-107.

[15] Wei Wei, Liu Ying, Mei Shengwei, et al. Study on residual flux evaluation method based on variable-regional integral during the voltage attenuation process[C]//2019 IEEE Innovative Smart Grid Technologies, Chengdu, China, 2019: 954-959.

[16] Yuan Weiying, Zhang Hua, Shangguan Yunqi, et al. Analysis on method of calculating transformer residual flux by using the integration of port-voltage waveform and its implementation[C]//2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, 2017: 1-4.

[17] 刘涛, 刘鑫, 梁仕斌, 等. 基于极性变化直流电压源的铁磁元件铁心剩磁通测量方法[J]. 电工技术学报, 2017, 32(13): 137-144.

Liu Tao, Liu Xin, Liang Shibin, et al. Residual flux measuring method on the core of ferromagnetic components based on alternating polarity DC voltage source[J]. Transactions of China Electrotechnical Society, 2017, 32(13): 137-144.

[18] 张书琦, 孙淑艳, 李刚, 等. 基于磁通实时跟踪的单相四柱式变压器典型工况剩磁特性[J]. 高电压技术, 2021, 47(2): 732-742.

Zhang Shuqi, Zhang Shuyan, Li Gang, et al. Residual flux characteristics of transformer with single-phase four-limb core under typical condition based on real-time flux tracking[J]. High Voltage Engineering, 2021, 47(2): 732-742.

[19] Abeywickrama N, Serdyuk Y V, Gubanski S M. Effect of core magnetization on frequency response analysis (FRA) of power transformers[J]. IEEE Transactions on Power Delivery, 2008, 23(3): 1432-1438.

[20] 赵志刚, 徐曼, 胡鑫剑. 基于改进损耗分离模型的铁磁材料损耗特性研究[J]. 电工技术学报, 2021, 36(13): 2782-2790.

Zhao Zhigang, Xu Man, Hu Xinjian. Research on magnetic losses characteristics of ferromagnetic materials based on improvement loss separation model[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2782-2790.

[21] 吴德会, 刘志天, 王晓红, 等. 基于微分磁导率的铁磁性材料无损检测新方法[J]. 仪器仪表学报, 2017, 38(6): 1490-1497.

Wu Dehui, Liu Zhitian, Wang Xiaohong, et al. New NDT method for ferromagnetic materials based on differential permeability[J]. Chinese Journal of Scientific Instrument, 2017, 38(6): 1490-1497.

[22] 焦在滨, 马涛, 屈亚军, 等. 基于励磁电感参数识别的快速变压器保护[J]. 中国电机工程学报, 2014, 34(10): 1658-1666.

Jiao Zaibin, Ma Tao, Qu Yajun, et al. A novel excitation inductance-based power transformer protection scheme[J]. Proceedings of the CSEE, 2014, 34(10): 1658-1666.

[23] 金雷, 谢齐家, 罗维, 等. 基于绕组变形测量的电力变压器剩磁大小估算[J]. 变压器, 2019, 56(10): 61-64.

Jin Lei, Xie Qijia, Luo Wei, et al. Estimate of remanence of power transfomer based on measurement of winding deformation[J]. Transformer，2019, 56(10): 61-64.

[24] 陶风波, 张刚, 李建生, 等. 基于局部磁滞回线斜率的变压器铁心剩磁估算[J]. 变压器, 2019, 56(2): 27-33.

Tao Fengbo, Zhang Gang, Li Jiansheng, et al. Remanent magnetism estimation of transformer core based on local hysteresis loop slope[J]. Transformer，2019, 56(2): 27-33.

[25] Gu Yalan, Liu Shengchao, Wang Dong, et al. A generalized moving average filter for active power filter applications[C]//2019 IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, Canada, 2019: 428-433.

Residual Flux Measurement Method of Power Transformer Based on Extreme Value of Transient Current Difference

Ren Yuzhan1,2Wu Shipu1,2Wang Youhua1,2Liu Chengcheng1,2Huo Cailing1,2

（1. State Key Laboratory of Reliability and Intelligence of Electrical Equipment Hebei University of Technology Tianjin 300130 China 2. Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability of Hebei Province Hebei University of Technology Tianjin 300130 China）

When a transformer is energized under no-load conditions, the magnetizing inrush current will have adverse effects on the power grid and equipment. In order to effectively weaken the residual flux density in the iron core to reduce the occurrence probability of magnetizing inrush current, it is necessary to measure the magnitude and direction of the residual flux density. Based on the electromagnetic transient characteristics of magnetic materials, a method for measuring the residual flux density of applied DC voltage was proposed in this paper. The residual flux density led to different transient current waveforms in the winding under positive and negative voltage. Combined with the field-circuit coupling analysis method, the relationship between the residual flux density and the extreme value of the transient current difference was established. In order to improve the accuracy of the measurement, the square core to be tested was modeled and analyzed, and suitable test circuit parameters were selected. According to the results of finite element calculation, the empirical formula between the residual flux density and the extreme value of the transient current difference was obtained, which laid a foundation for quantitative test of the residual flux density. Finally, a measurement platform was built, and the iron core to be tested was studied by experiments. The measurement results verify the feasibility and accuracy of the proposed method.

Power transformer, magnetizing inrush current, residual flux, field-circuit coupling analysis, transient current difference

10.19595/j.cnki.1000-6753.tces.210115

TM406

国家自然科学基金资助项目（51877065）。

2021-01-21

2021-07-23

任于展 男，1997年生，硕士研究生，研究方向为工程电磁场与磁技术。E-mail：1094500481@qq.com

汪友华 男，1964年生，教授，博士生导师，研究方向为工程电磁场与磁技术、磁材料特性的建模与测量、电磁冶金与全局优化设计。E-mail：wangyi@hebut.edu.cn（通信作者）

（编辑 赫蕾）