脉冲噪声下基于NAT函数的LFM信号参数估计

金 艳, 赵大地, 姬红兵

(西安电子科技大学电子工程学院, 陕西 西安 710071)

0 引 言

线性调频(linear frequency modulation,LFM)信号具有分辨率高和截获概率低等特点,是一类具有代表性的非平稳信号,常应用于水声、雷达、生物医学、地质勘探等领域。中心频率和调频斜率包含有LFM信号的相位参数信息,所以LFM信号的参数估计方法研究具有重要价值。基于最大似然(maximum likelihood,ML)原理的LFM信号分析方法计算精度高,其误差估计曲线接近克拉美罗下界(Cramer-Rao lower bound,CRLB),但该方法需要优化损失函数,计算量大且实时性差。分数阶傅里叶变换(fractional Fourier transform, FrFT)是一种应用广泛的非平稳信号分析方法,LFM信号的能量聚集性随着FrFT阶数的不同而改变,通过搜索FrFT域的峰值坐标,再由峰值坐标与信号相位参数的转换公式,完成信号参数估计,该方法步骤较为复杂。吕氏分布(Lv’s distribution, LVD)方法是一种将LFM信号直接分解在中心频率-调频斜率(centroid frequency chirprate,CF-CR)域进行研究的时频分析方法。经LVD变换后,LFM信号在LVD域呈现为峰值。与FrFT方法不同,LVD免去从峰值坐标到信号相位参数转换的步骤,由CF-CR平面上的坐标即可直接获得LFM信号的中心频率和调频斜率。

然而,上述LFM信号参数估计方法在脉冲噪声环境下性能急剧下降甚至失效。对于具备明显脉冲特性,且概率密度函数拖尾厚重的噪声,α稳定分布噪声模型能够对其准确描述。但α稳定分布的二阶和高阶矩不具备有界性,所以传统的信号处理方法在α稳定分布噪声下不再适用。对此,近年来有研究者提出了基于相关熵核函数内在稳健性的信号处理方法;也有学者提出了首先采用非线性方法对接收信号进行脉冲噪声抑制,使含有α稳定分布噪声的信号经非线性处理后,信号的二阶统计量存在,再采用常规信号处理方法完成有用的信号分析和提取,如分数低阶(fractional lower order,FLO)方法、基于M估计的Myriad滤波和Meridian滤波方法、基于非线性幅值变换(nonlinear amplitude transformation,NAT)函数的方法等。

以上方法虽然可较为有效地抑制α稳定分布噪声,但也存在明显缺陷,如传统相关熵的核函数为高斯核,仅适用于信噪比较高的环境下,且由于核函数自身缺陷,相关熵方法无法抑制幅值相近的脉冲噪声;FLO方法虽能较好地抑制噪声,但需要获得噪声先验信息,且其阶数的取值缺乏理论依据,实时性差;Myriad及Meridian滤波方法计算复杂度高,且在脉冲性强的噪声环境下性能下降剧烈;基于非线性幅值变换函数的方法是将含噪信号进行预处理,在不改变参数信息的基础上抑制噪声,已有研究将神经网络中常用的激活函数,如Sigmoid函数和tanh函数用于非高斯信号处理领域,这两种函数相较于FLO方法无需在参数估计前获取噪声信息,但Sigmoid函数和tanh函数抑制脉冲噪声的能力弱于分数低阶方法,因此这两种NAT函数抑制脉冲噪声的能力有限。

针对现有的抑制脉冲噪声方法存在的计算复杂度高、需获取噪声先验信息和抑噪能力有限等问题,论文设计了两种新的NAT函数,即具有衰减特性的A-NAT函数和具有限幅特性的IB-NAT函数,并从计算复杂度和抑制脉冲噪声能力两方面将两种函数进行对比,确定其适用范围。将经过函数变换后的信号进行LVD分析,通过CF-CR域上对应的峰值坐标即可直接实现LFM信号的参数估计。本文所提方法计算复杂度低,实时性高,且无需获取噪声先验信息。

1 α稳定分布脉冲噪声模型

由于α稳定分布不具备闭式的概率密度解析式,因此一般采用特征函数表示:

()=exp{j-||[1+jsgn()(,)]}

(1)

其中,

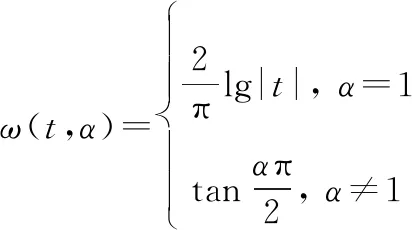
(2)

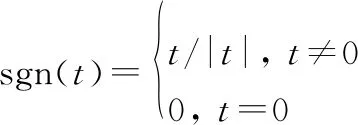
(3)

式中:sgn()为符号函数;表示位置参数,且-∞<<+∞,其值决定了分布的中心位置;特征指数的取值为0<≤2,值越小则噪声的脉冲特性越强,特别地,当=1时,该分布变为柯西分布,=2时变为高斯分布;尺度参数取值为>0,用于衡量样本偏离均值的程度,类似于高斯分布的方差;为对称参数,且-1≤≤1,表征分布的对称程度,=0时即为对称稳定分布(symmetric α stable,SαS)。由于稳定分布噪声的方差不存在,常规信噪比无意义,所以采用广义信噪比(generalized signal to noise ratio,GSNR):

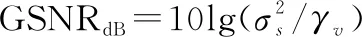
(4)

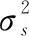
2 非线性幅值变换函数

由于含有随机大幅值脉冲,稳定分布的二阶统计量不具备有界性,所以基于二阶矩的常规参数估计方法在稳定分布噪声环境下失效。FLO方法将稳定分布噪声处理转化为对其脉冲幅度的抑制,可实现脉冲噪声中有用信号的分析与提取。受此启发,本文构造两种新的可抑制大幅值脉冲的NAT函数,使含有稳定分布噪声的信号非线性变换后,信号的二阶统计量存在,进而使得后续信号分析中常规参数估计方法有效可行。

当含噪信号包含大幅值脉冲时,所构造的非线性函数需能够有效抑制噪声的大幅值,因而可考虑具有如下衰减特性的attenuation-NAT (A-NAT)函数或具有有界单调递增特性的increasing bounded-NAT(IB-NAT)函数:

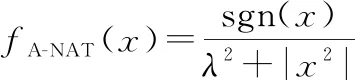
(5)

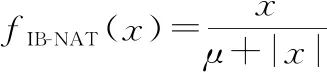
(6)

式中：sgn()为式(3)所示的符号函数,若为复数,||为的模值;()的值域为(-1,1),()值域为(-1,1)。由式(5)和式(6)可知,()的分母中含有二次项,()只包含一次项,因此A-NAT函数的计算复杂度要高于IB-NAT函数。

图1所示为本文构造的A-NAT函数()与IB-NAT函数()曲线。图1(a)为A-NAT函数()曲线,由图可知,所构造的A-NAT函数具有非线性特性且是奇对称的,该函数在=0附近(即临零区域)迅速达到极值后,在定义域的其余范围均处于衰减状态,且随着||增大,函数值趋于0。因此,A-NAT变换可将强脉冲值压缩映射至()值域范围(-1/,1)内,且脉冲值越大,经A-NAT变换后的函数值越小。由图1(b)可以看出,所构造的IB-NAT函数具有单调递增和对称有界特性。IB-NAT函数在临零区域内近似线性,随着||的增大,函数值趋于值域边界。

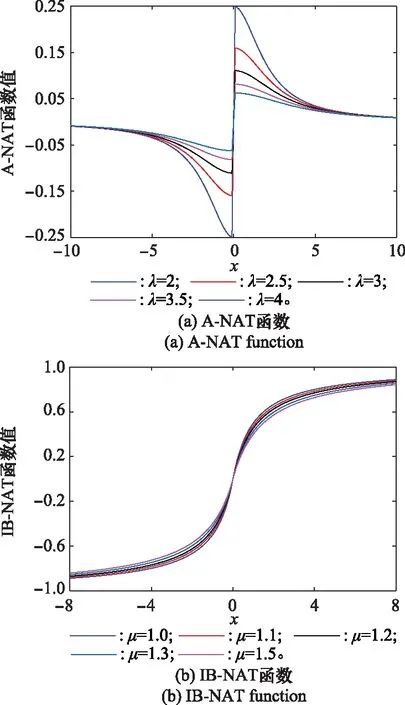
图1 两种新的NAT函数曲线Fig.1 Two new NAT function curves

图2和图3是在GSNR为-3 dB,特征指数取不同值时,对LFM信号进行200次蒙特卡罗实验,得到信号中心频率、调频斜率与归一化均方根误差(normalized root mean square error,NRMSE)的关系曲线。由实验结果可知,A-NAT函数中的参数最优取值为2≤≤3;IB-NAT函数中的参数最优取值为1≤≤1.5。

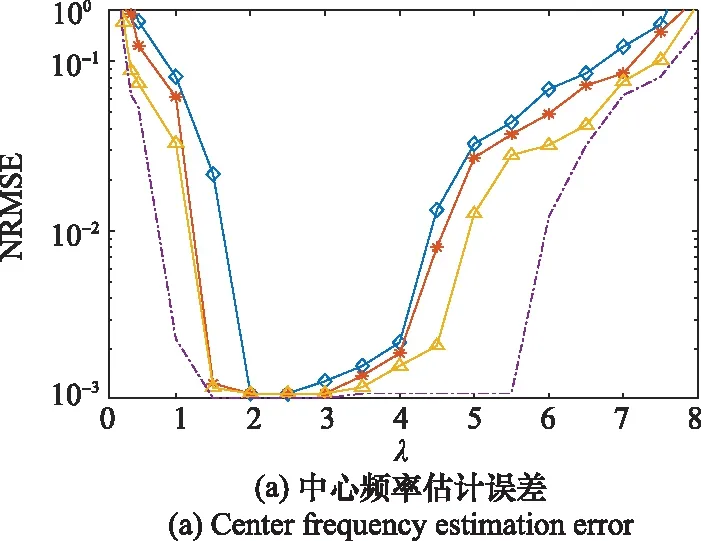
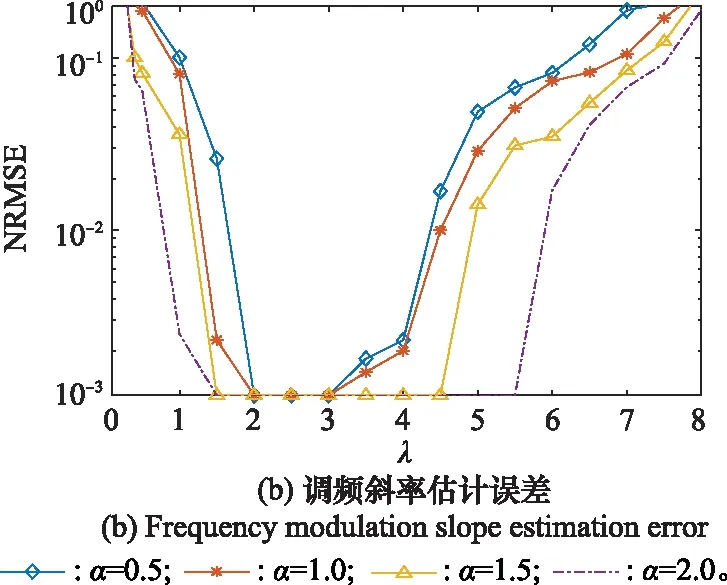
图2 A-NAT函数不同参数下信号估计误差Fig.2 Estimation error of A-NAT function for signals under different parameters

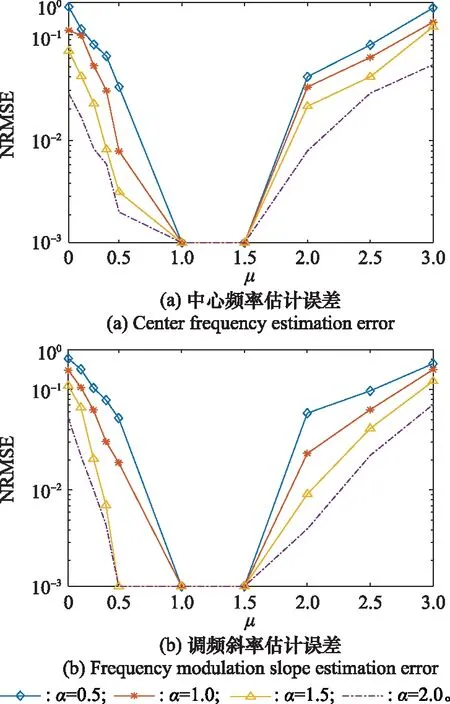
图3 IB-NAT函数在不同参数下对信号估计误差Fig.3 Estimation error of IB-NAT function for signals under different parameters

分别取=2和=1,得到图4和图5所示NAT变换后的稳定分布噪声方差。可知,稳定分布经A-NAT和IB-NAT非线性幅值变换后的方差均有界,且在=0.3的脉冲性极强的条件下仍收敛,即通过A-NAT或IB-NAT变换后,稳定分布的二阶矩有界,因此所构造的A-NAT函数和IB-NAT函数均能对脉冲噪声起到抑制作用。

对比图4和图5可知,稳定分布经A-NAT变换后的方差随值减小而减小,而经IB-NAT变换后的样本方差则随值减小而增大。这是因为当值减小时,稳定分布出现偏离分布中心的大幅值异常脉冲值的概率增大,不同的异常值经A-NAT函数衰减变换后分布于值域内的不同位置处;而IB-NAT函数是将所有异常值均变换到值域边界,在较小的情况下,大量异常值密集地分布于值域边界附近,从而造成方差增大。可知,IB-NAT函数是通过限幅作用将脉冲噪声限制在值域边界,而A-NAT函数具有衰减特性,噪声的脉冲性越强,()对噪声所起到的抑制作用也越强。因此,在∈[0.1,0.8)的脉冲性极强的条件下,A-NAT函数抑制噪声的性能优于IB-NAT函数。

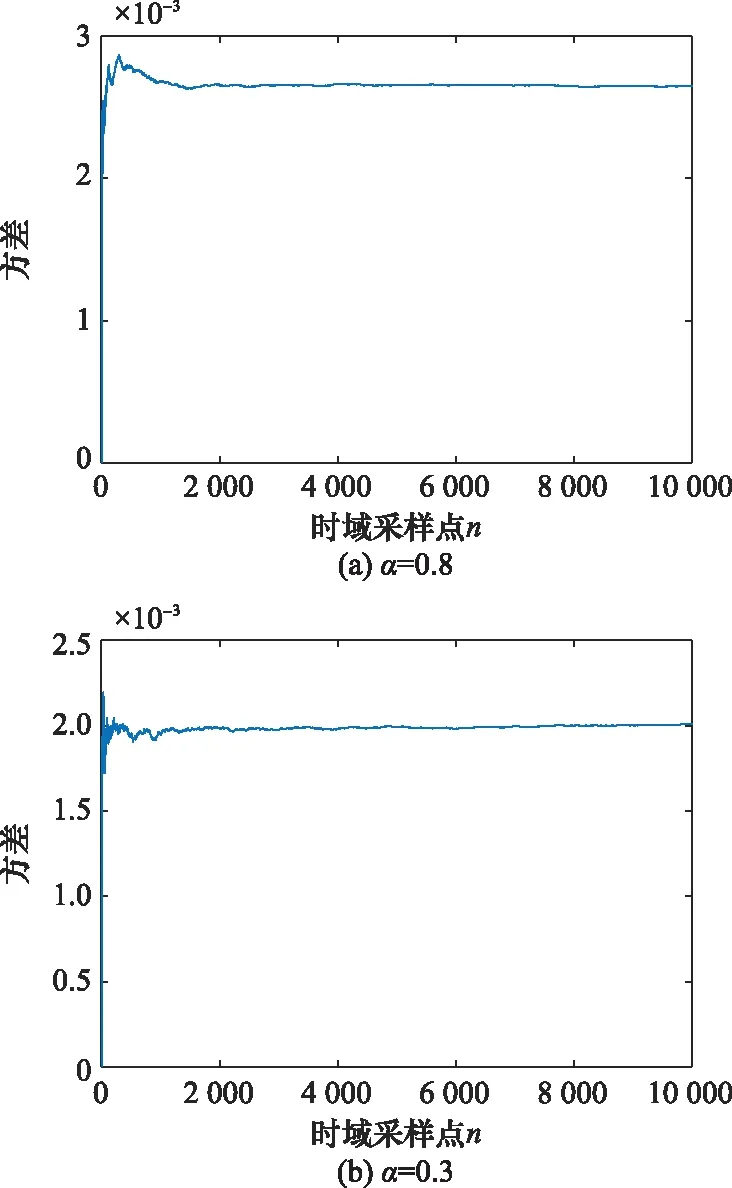
图4 A-NAT变换后的α稳定分布方差Fig.4 Variance of α-stable distribution after A-NAT transformation

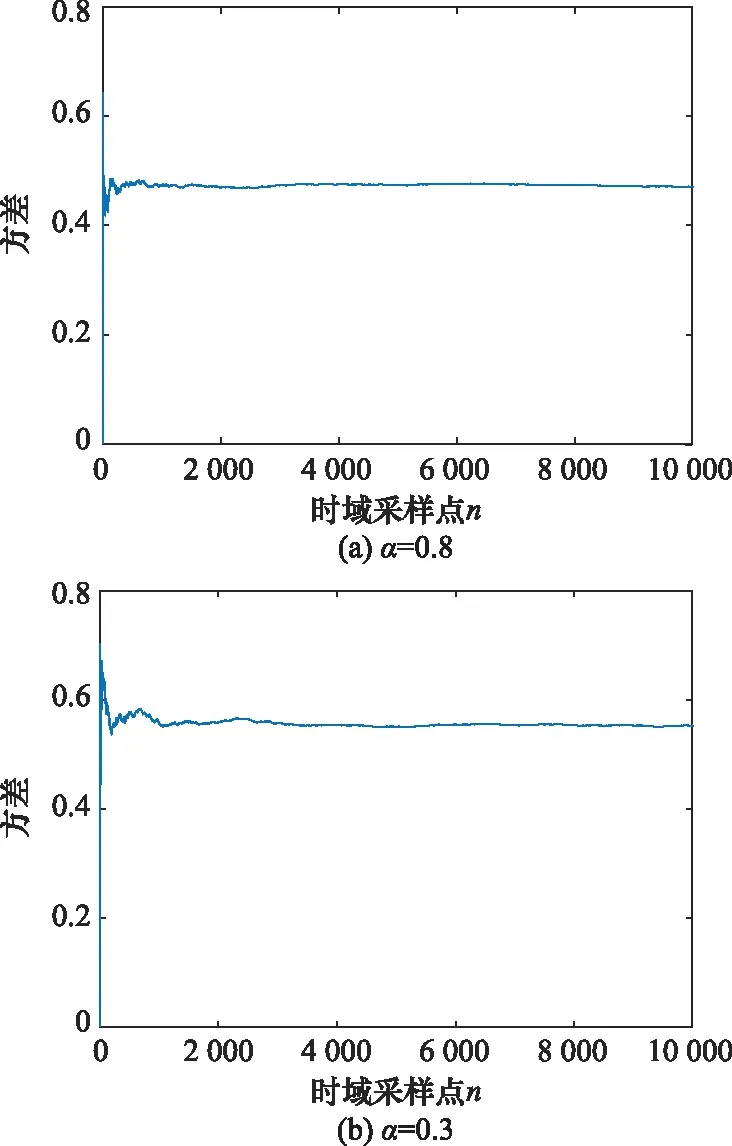
图5 IB-NAT变换后的α稳定分布方差Fig.5 Variance of α-stable distribution after IB-NAT transformation

FLO算子能够较为有效地抑制脉冲噪声,但FLO算子需要获取噪声先验信息。与FLO算子()=[][26]相比,A-NAT函数在临零区域之外的定义域内均处于衰减状态,IB-NAT函数的递增趋势更缓慢且有界。因此,本文所构造的两种非线性幅值变换函数可更有效抑制脉冲噪声,且基于这两种函数的参数估计方法无需噪声先验信息。由此提出命题1并给予证明。

为服从稳定分布的大幅值脉冲样本,设经过A-NAT变换后的函数值为=(),经IB-NAT变换后的函数值为=(),则在脉冲噪声环境下满足(||)<(||)<(|([])|),其中0<<2,<>=·||||。

设的概率密度函数为(),则有

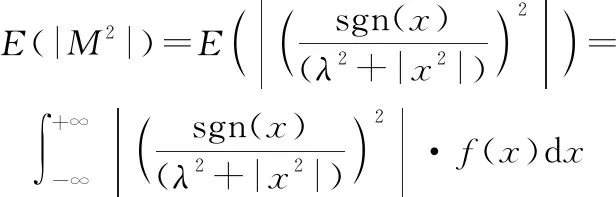
(7)

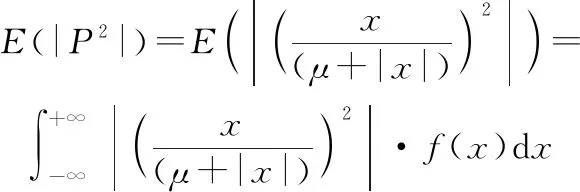
(8)

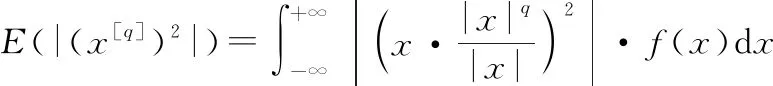
(9)

由于概率密度函数()≥0,所以只需证明在-∞<<+∞时，

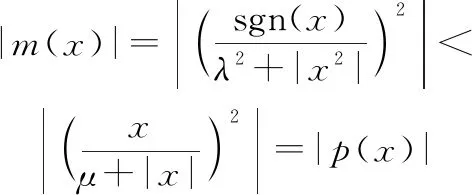
(10)

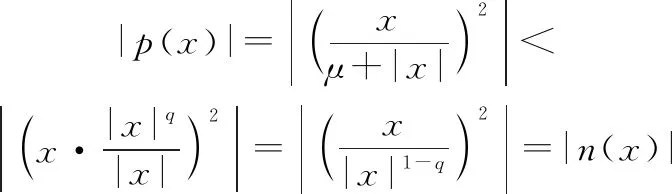
(11)

因为()=(-),()=(-),则只需证明0≤<+∞时，以上不等式成立,当0≤<+∞时，式(10)和式(11)可分别化为

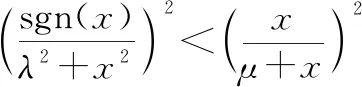
(12)

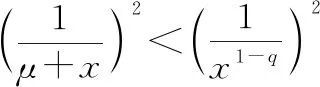
(13)

即等价于证明

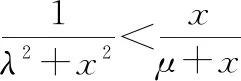
(14)

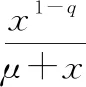
(15)

因为为服从稳定分布的大幅值脉冲样本,∈[2,4],∈[1,15],∈(0,2),则式(14)和式(15)成立,即式(10)和式(11)成立,从而命题1得证。因此,具有脉冲特性的样本经过A-NAT或IB-NAT变换后均存在有限二阶矩,且A-NAT函数和IB-NAT函数脉冲噪声抑制性能均优于FLO函数,其中A-NAT函数的抑制效果最优。

LFM信号经A-NAT或IB-NAT函数变换后仅幅值发生变换,相位信息不变。

设LFM信号为()=exp(j2π+jπ),为信号幅度,为信号的初始频率,是调频斜率,则有

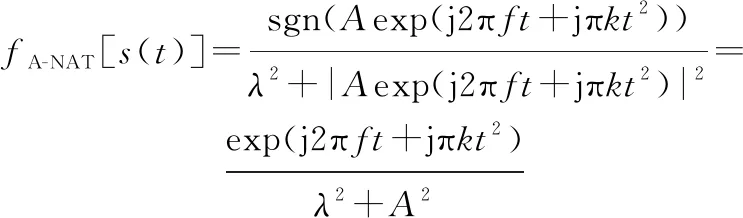
(16)

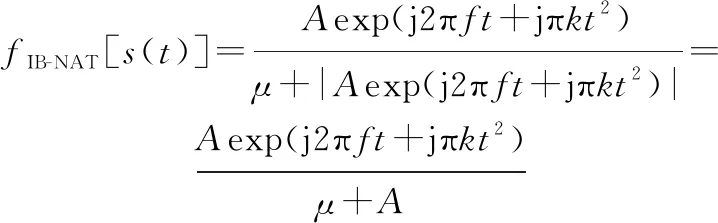
(17)

证毕

3 基于NAT函数的参数估计

3.1 LVD变换

LVD方法是一种比传统时频分析更为高效的LFM信号处理方法。常规的LFM信号分析方法是在时频域对其进行参数估计,而LVD方法是将信号分解在CF-CR域,LFM信号经LVD变换后表现为峰值,通过该峰值所对应的CF-CR平面坐标,即可得到LFM信号的调频斜率与中心频率估计值。

LFM信号()的表达式可写为

()=ej2π+jπ

(18)

式中：表示信号幅值；和分别表示LFM信号的中心频率和调频斜率。()的对称参数瞬时自相关函数(parametric symmetric instantaneous autocorrelation function,PSIAF)定义为

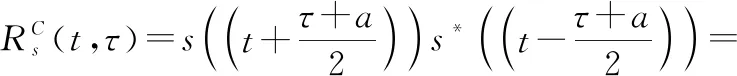
(19)

式中:为延迟常数,一般取其最优值1；*为共轭符号。通过对时间变量做如下尺度变换可以解除其与延时的耦合关系:

(20)

式中：为尺度因子,时间变量经过尺度变换,为=(+),此时PSIAF为

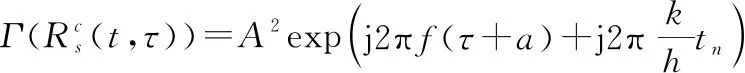
(21)

再对,作二维傅里叶变换,即得LVD的表达式:

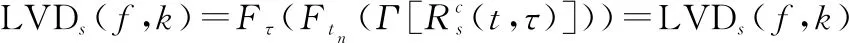
(22)

式中:{·}表示傅里叶变换。LFM信号的LVD为

望虞河常熟水利枢纽于2010年11月起开始实施更新改造工作，改造工程于2011年3月10日前完成。改造期间常熟水利枢纽泵站无法正常投入运用，仅能通过节制闸自引。望虞河望亭水利枢纽更新改造工程于2010年11月28日正式开工。根据施工期工程运行维护要求，望亭水利枢纽需开展水下检查暂停运用。同时，施工期间望亭水利枢纽闸门也无法全部投入运用。

LVD(,)=exp(j2π)·(-)(-)

(23)

可以看出,仅当=,=时,LVD取非零值。

利用峰值检测方法搜索LVD时频谱峰值坐标(,),为LFM信号中心频率的估计值,是调频斜率的估计值。

3.2 基于NAT函数的参数估计

设信号()是脉冲噪声环境下的LFM信号,即

()=()+()

(24)

式中:()是稳定分布脉冲噪声。()和()分别是信号()经A-NAT变换、IB-NAT变换后的信号,即

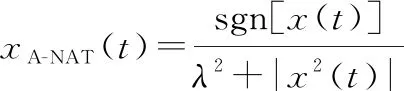
(25)

(26)

式(25)和式(26)作LVD变换,在LVD域搜寻峰值点,根据该峰值对应的CF-CR平面坐标值即可完成LFM信号的参数估计。

4 仿真实验与结果分析

本文仿真采用声纳工程中的LFM信号参数:中心频率=7.5 kHz,调频斜率=1 kHz/s,采样频率=25.6 kHz,采样点数=2.56×10。噪声环境为SαS分布噪声。

4.1 不同方法仿真结果及分析

如图6(b)～图6(f)所示,在α=0.8,GSNR=-2 dB的噪声环境下,分别采用LVD方法、基于Myriad滤波的MY-LVD、基于FLO方法的FLO-LVD与本文提出的A-NAT-LVD、IB-NAT-LVD方法对含有脉冲噪声的LFM信号进行处理并对比。

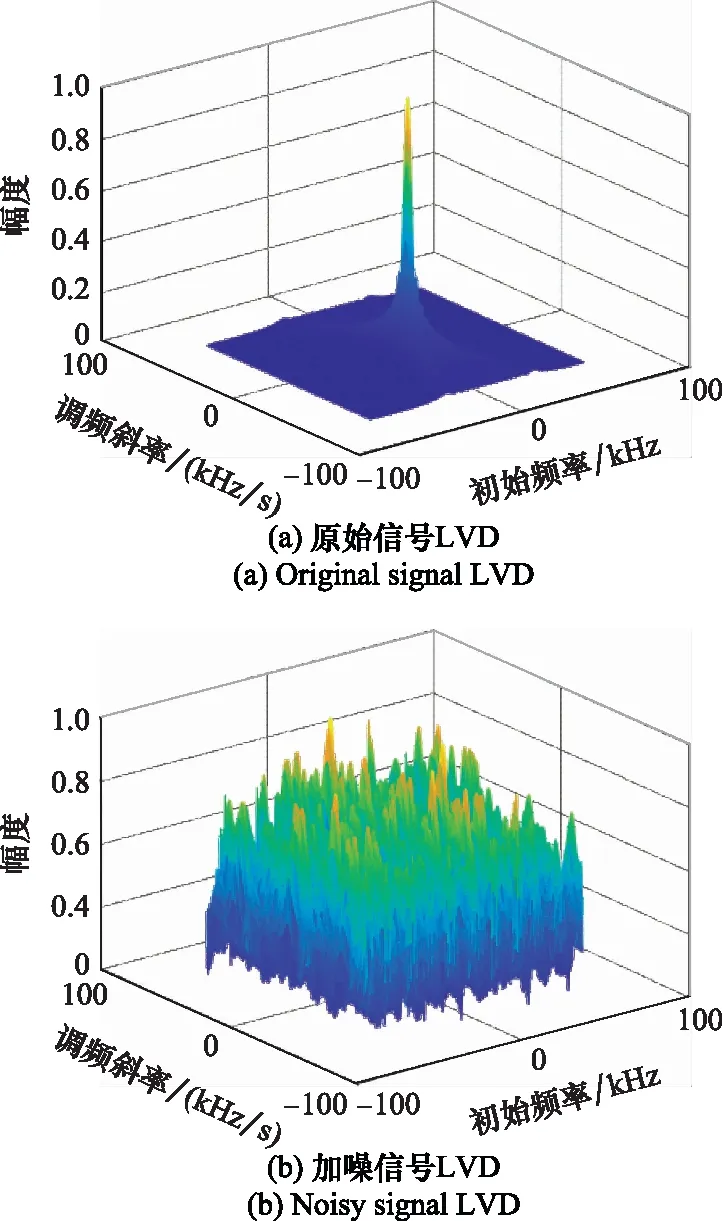
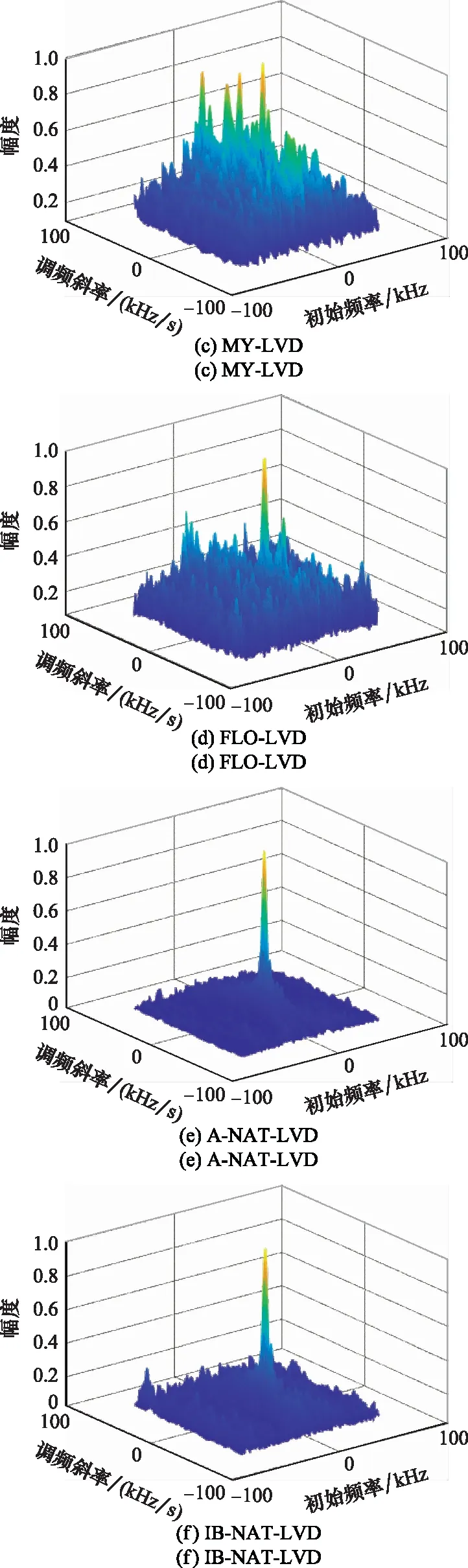
图6 不同方法下的LVDFig.6 LVD under different methods

图6(a)是在无噪声的理想环境下原始LFM信号的LVD三维图,图中峰值明显,通过峰值坐标即可估计出信号的中心频率和调频斜率值;图6(b)是在脉冲噪声下,信号的LVD三维图,含有参数信息的峰值被噪声覆盖,无法进行参数估计;图6(c)是基于Myriad滤波的MY-LVD所对应的LVD三维图,图中存在多个峰值,无法根据最大峰值点对应的CF-CR平面坐标提取LFM信号参数信息;采用基于FLO(阶数为0.2)算子的FLO-LVD方法得到了图6(d),可见,脉冲噪声已被抑制,虽存在部分凸起峰值,但最大峰值明显,可以提取参数信息;分别采用A-NAT-LVD方法和IB-NAT-LVD方法得到了图6(e)和图6(f),可以看出,采用本文所提两种方法,脉冲噪声得到有效抑制,几乎无残余噪声,且均存在明显峰值。综上,A-NAT-LVD和IB-NAT-LVD方法可有效抑制脉冲噪声,且性能优于FLO-LVD方法,与本文命题1所述理论一致。

4.2 不同方法性能比较及分析

本节通过NRMSE来描述不同方法抑制脉冲噪声的性能差异。在不同的GSNR环境下,经200次蒙特卡罗实验,实验结果如图7和图8所示。

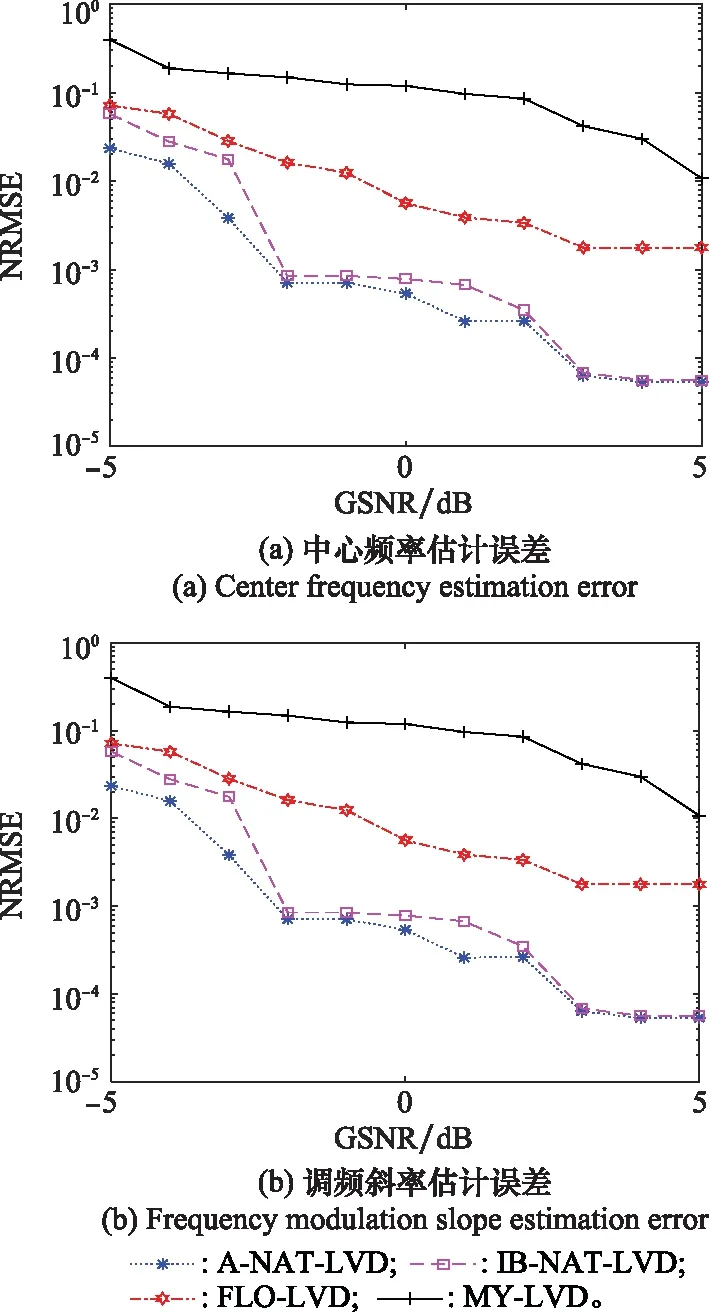
图7 α=0.8时LFM信号参数估计误差Fig.7 Error of LFM signal parameter estimation when α=0.8

根据图7,MY-LVD方法在=0.8和较高GSNR的噪声条件下,对LFM信号的参数估计仍存在偏差;FLO-LVD方法在=0.8的脉冲噪声环境下,当GSNR≥-1 dB时可以实现有效参数估计,但当GSNR<-1 dB时估计性能下降明显;A-NAT-LVD和IB-NAT-LVD方法在GSNR≥-2 dB时可较为精确地对LFM信号的中心频率和调频斜率进行参数估计。由图8可知,在=15的稳定分布噪声环境下,MY-LVD方法对LFM信号的参数估计误差比在=0.8的条件下有所减小,但仍存在偏差;FLO-LVD方法在GSNR≥-2 dB条件下可较为精确地对LFM信号的中心频率和调频斜率进行参数估计;IB-NAT-LVD方法在GSNR≥-3 dB时,A-NAT-LVD方法在GSNR≥-4 dB时可较为精确地估计出LFM信号参数。

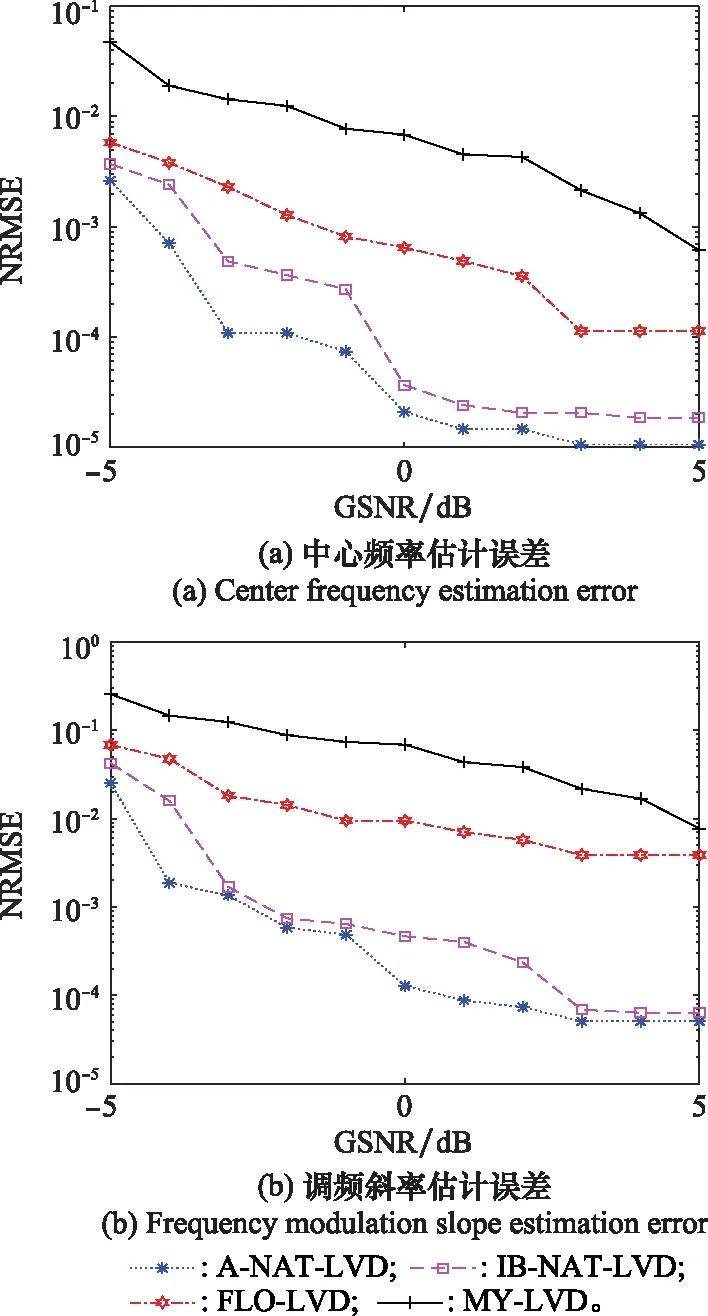
图8 α=1.5时LFM信号参数估计误差Fig.8 Error of LFM signal parameter estimation when α=1.5

比较图7和图8可知,采用A-NAT-LVD和IB-NAT-LVD方法可以在脉冲性较强,GSNR较小的环境下实现对LFM信号参数的准确估计,随着脉冲强度的增大,FLO-LVD和MY-LVD方法的性能下降,而A-NAT-LVD和IB-NAT-LVD方法仍具有较强的稳健性。

为进一步分析所提方法适用的稳定分布噪声范围,以及验证命题1中提出的()抑制脉冲噪声的能力强于(),在GSNR=-2 dB的条件下,改变特征指数的值并进行200次蒙特卡罗实验,结果如图9所示。可见,A-NAT-LVD方法和IB-NAT-LVD方法在≥0.8脉冲噪声环境下性能接近,且抑制噪声能力均优于FLO-LVD方法和MY-LVD 方法;在<0.8冲击性极强的噪声环境下,由于A-NAT函数对大幅值脉冲的衰减作用,A-NAT-LVD仍具有稳健的参数估计性能。IB-NAT-LVD 方法在<0.8的环境下抑制脉冲噪声的能力不及A-NAT-LVD方法,但仍优于FLO-LVD和MY-LVD方法。

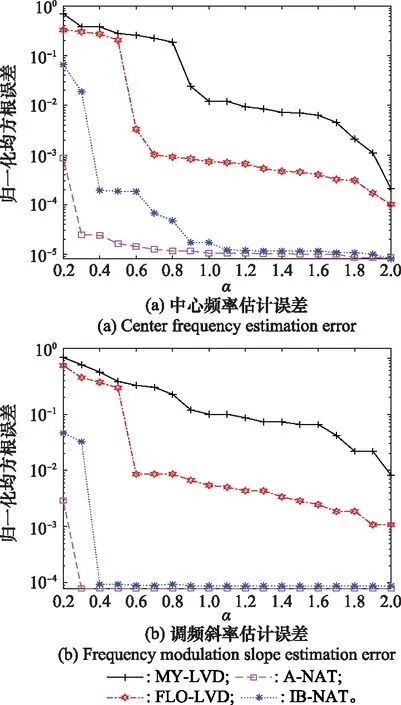
图9 不同α值下参数估计误差比较Fig.9 Comparison of parameter estimation error under different α values

因此,在<0.8脉冲特性极强的噪声环境下,选择抑噪性能最优的A-NAT-LVD方法;在≥0.8的噪声环境下,可选择计算复杂度更低的IB-NAT-LVD方法替代现有的脉冲噪声下LFM信号参数估计方法。

5 结 论

为解决脉冲噪声环境下传统LFM信号参数估计方法性能下降剧烈甚至失效的问题,本文构造了A-NAT函数和IB-NAT函数,提出了基于所构造NAT函数的参数估计新方法。通过对命题1和命题2的证明可知,含噪信号经A-NAT或IB-NAT变换后的二阶矩存在有界值,且仅幅值变化,相位信息不变,IB-NAT函数相较于A-NAT函数具有更低的计算复杂度,而在抑制脉冲噪声能力方面,()>()>()。首先对脉冲噪声背景下的LFM信号进行A-NAT或IB-NAT变换,再对变换后的信号进行LVD分析,即可完成LFM信号的参数估计。与基于FLO函数和Myriad滤波的参数估计方法对比,本文所提方法无需噪声先验信息,能够抑制不同强度的脉冲噪声,且具有良好的鲁棒性。