航空发动机短舱泄压门冲击载荷结构拓扑优化技术研究

侯亮 柴象海 白国娟 金智献

摘要：部分航空发动机零部件的工作载荷类型属于冲击载荷，采用静力学强度判定准则无法证明其设计符合性，导致无法采用静力学载荷对其进行结构优化，需要建立基于冲击动力学载荷的航空发动机结构拓扑优化方法。以航空发动机泄压门铰链为研究对象，通过结构冲击动力学载荷拓扑优化技术研究，建立短舱腔压导致的泄压门弹开载荷作用下拓扑优化方法，提高泄压门铰链强度裕度，解决泄压门强度考核试验中出现的铰链断裂问题。基于冲击动力学载荷的航空发动机结构拓扑优化方法，能够避免动力学等效静载荷误差，优化结果更加符合载荷传力特征，为航空发动机零部件减重和应力降低优化提供了有效的解决途径。

关键词：航空发动机；拓扑优化；冲击动力学；应力；减重

中图分类号：V214.1文献标识码：ADOI：10.19452/j.issn1007-5453.2022.01.007

基金项目：国家重点研发计划资助（2018YFB1106400）

我国当前航空发动机设计方法偏于保守，缺乏更加先進高效的设计手段，虽然静强度、刚度等指标满足设计要求，但重量（质量）指标远低于国际先进设计水平。结构优化是提升航空发动机设计水平的重要手段，但缺少应用示范，尤其是基于冲击动力学载荷的航空发动机结构拓扑优化方法有待建立[1-2]。近年来，随着基于混合元胞自动机（HCA）方法的结构拓扑优化设计研究的日益深入，为基于冲击动力学载荷的航空发动机减重优化奠定了基础，本文基于HCA方法对航空发动机短舱泄压门拓扑优化理论和方法进行探索。

1冲击动力学载荷结构拓扑优化理论与方法

1.1结构拓扑优化理论与方法

最优化设计理论和方法在机械结构设计中得到了深入的研究和广泛的应用。根据设计变量的类型，结构优化设计可以分为尺寸优化、形状优化、拓扑与布局优化三个层次。其中，拓扑优化是结构设计领域的关键和难题，因为结构拓扑形态在很大意义上，基本决定了结构的功能、载荷、约束和材料配置等的适用范围[3-5]。用现有结构、材料、力学解析法（有限元法等）和结构优化方法，由于表达结构拓扑设计的自由度庞大，只能在相对结构初始拓扑形态变化较小的范围内，实现结构的拓扑形态的再设计和强度、应力分布等的再校核。

1.2基于冲击动力学载荷的结构拓扑优化方法

元胞自动机（CA）是定义在一个由具有离散、有限状态的元孢组成的元胞空间上，并按照一定局部规则，在离散的时间维度上演化的动力学系统，CA以其组成单元的简单规则性，单元之间作用的局部性和信息处理的高度并行性，并表现出复杂的全局性等特点而备受关注，成为探索复杂系统的一种有效工具[6-9]。

HCA算法是一种将元胞自动机原理与有限元分析结合起来的方法。利用元胞自动机离散性、自适应、自进化的特征，与有限元分析方法相结合，可以解决优化过程中复杂结构的力学分析问题，为有效进行结构的拓扑优化设计提供新的分析思路和技术手段。该方法不仅极大地减少了计算量，提高了求解效率，而且克服了数值不稳定问题，如棋盘格式问题和网格依赖性问题[10-11]。

HCA算法简单易懂，收敛性好，计算效率高，克服了数值不稳定问题，但目前只有些初步的研究，对于理论模型的构建，复杂问题的求解，技术环节的实现等方面还有待进一步发展。关于HCA算法进行结构拓扑优化设计，国内外建立了完善的理论基础和实现工具，但对于复杂问题的求解可行性尚有待验证。基于HCA算法，引入材料失效修正因子，对HCA算法进行改进，能够解决结构失效优化问题，扩充了HCA方法的适用范围[12-13]。

2航空发动机泄压门支架优化方法

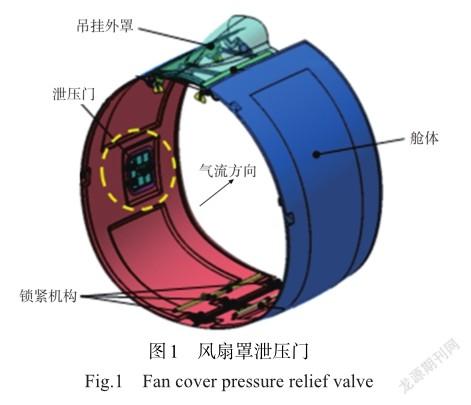
2.1泄压门结构及载荷特征

泄压门位于短舱风扇罩上的活动口盖，如图1所示，当风扇罩内部高压气体管路在某些工况下破裂时，管路内部高压气体泄漏导致风扇罩内部气压升高，当压力达到泄压门释放压力阈值时，泄压门打开使风扇罩内高压气体释放，避免封闭空间压力急剧升高导致风扇罩破裂。

飞行状态下泄压门受到风扇罩内部高压气体和风扇罩外部气流的共同作用打开，在地面状态下，泄压门仅受到风扇罩内部高压气体作用打开，内外压差为20000～35000Pa。当泄压门打开至某一角度时，泄压门受到限位挡块的限制，从而停止运动。

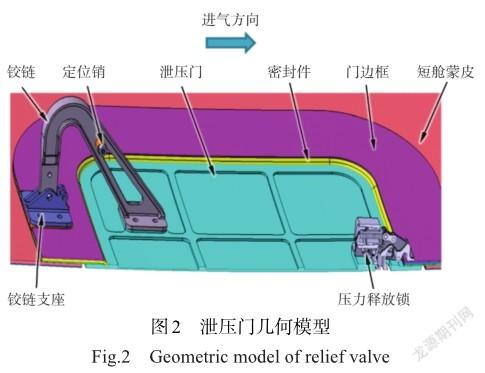
2.2泄压门铰链强度设计问题

泄压门几何模型如图2所示，由泄压门本体、铰链、铰链支座门边框、密封件等主要部件组成。泄压门本体通过螺栓与铰链连接，铰链通过转轴与铰链支座连接。泄压门上装有压力释放锁，当内部压力达到设定阈值时锁自动打开，泄压门开门释放压力。铰链支座和门边框通过螺栓固定在风扇罩上。泄压门打开时，铰链在支座上绕转轴旋转，当铰链接触限位凸台时，铰链停止转动。

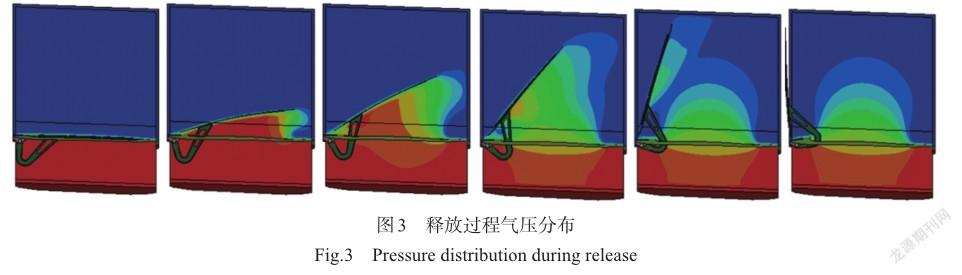
泄压门在风扇罩内部瞬态高压作用下的打开过程是流固耦合问题，通过显式动力学方法进行分析，流固耦合压力分布变化过程如图3所示。泄压门开启过程如图4所示。0ms时，泄压门在内部压力作用下开启，28ms铰链碰撞铰链支座限位凸台，开启角度达到最大位置。由于惯性作用，泄压门继续打开并折弯，铰链带动铰链支座运动使门边框产生变形。分析结果表明，泄压门打开到最大角度，铰链与铰链支座限位凸台发生碰撞，泄压门发生了弯折塑性变形，金属零件均发生较大塑性变形，需要对泄压门门板、铰链等结构进行优化，减少变形。

2.3泄压门铰链结构拓扑优化建模

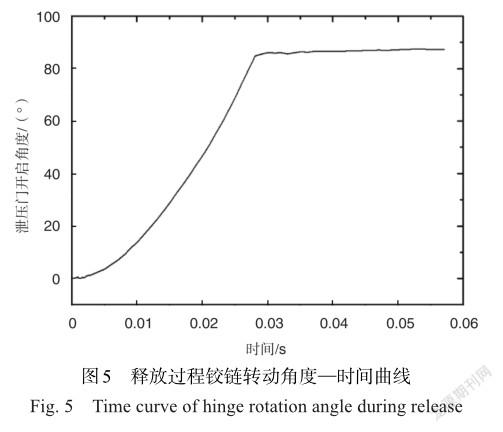
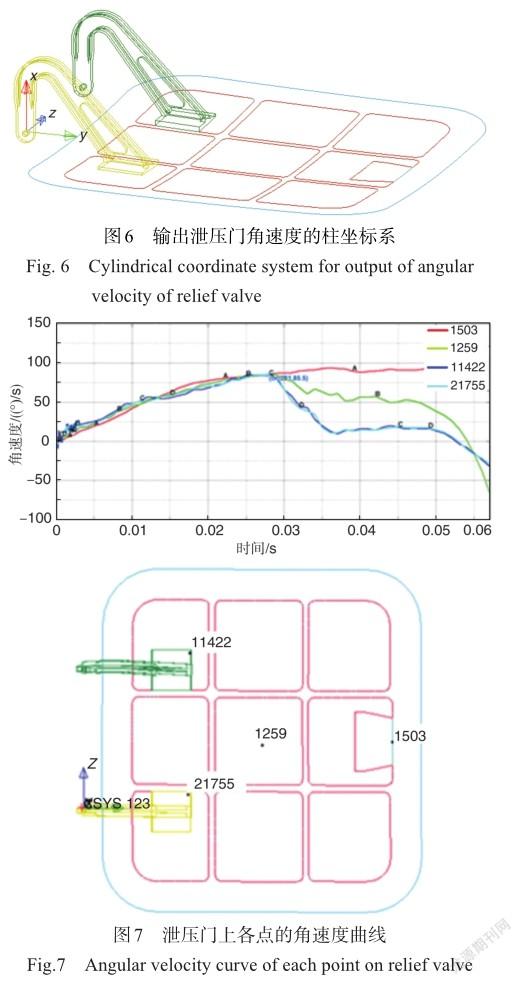
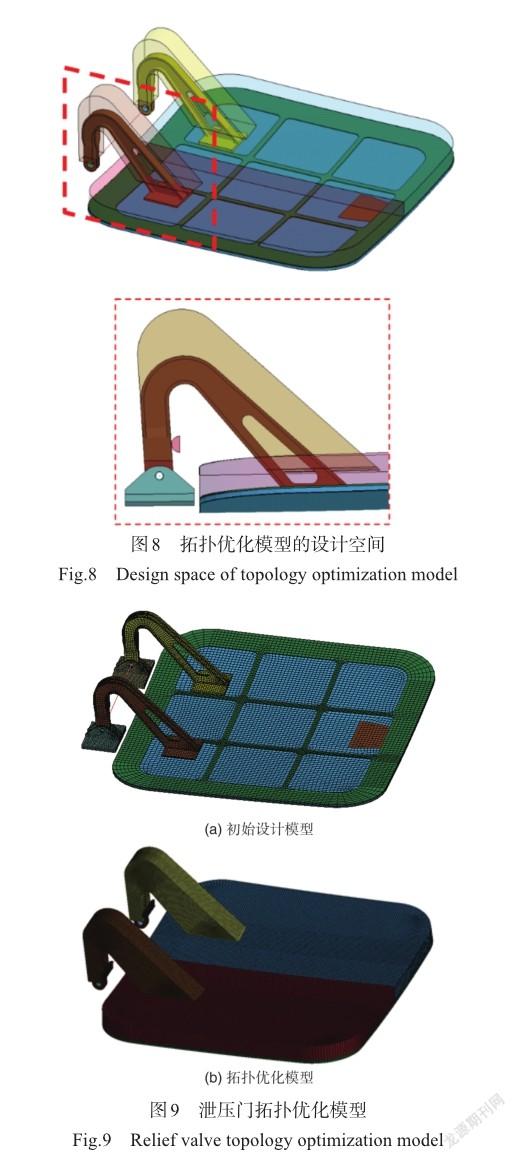
泄压门打开过程铰链转动角度随时间变化关系如图5所示。如图6所示，以铰链旋转轴为x轴，建立柱坐標系。在柱坐标系内输出泄压门的角速度，如图7所示。28ms时，铰链开始碰撞限位凸台时，泄压门上各点角速度为85.5rad/s，以此速度作为拓扑优化的初始条件。针对拓扑优化问题，通常在允许范围内放大设计空间，以得到较好的优化结果。泄压门拓扑优化的设计空间如图8所示。在原始模型基础上，对门板及铰链设计空间进行了放大，建立拓扑优化模型如图9所示。

泄压门设计空间采用实体单元划分网格，网格尺寸3mm，单元数量143190。泄压门门板为非设计空间，网格尺寸3mm，单元数量28638。铰链及支座有限元模型如图10所示，简化了转轴与支座铰链，铰链通过RBE2单元与铰接单元固定在固支的质点上。铰链设计空间采用实体单元划分网格，网格尺寸3mm，单元数量53568个，铰链及支座有限元模型信息见表1。

为了满足一定的工艺要求通常需要根据各个零件的特点对拓扑优化空间进行工艺约束，如图11所示，通常工艺约束有以下几种：（1）对称约束：优化结果按定义的平面对称；（2）挤出约束：对于梁等横截面优化，通常采用挤出约束。挤出约束通过单元集定义横截面；（3）铸造约束：铸造约束满足单向拔模或双向拔模的工艺条件，而且优化结果内部不存在空腔；（4）锻造约束：锻造约束满足双向拔模条件，同时要求定义最小厚度，优化结果不会产生孔洞；（5）封闭空间约束：这种约束不会产生封闭的内部空间，满足增材制造等工艺要求。

在算例中，对门板设计空间采用单向拔模约束，对铰链采用了双向拔模约束，如图12所示。

2.4泄压门铰链结构拓扑优化计算

对泄压门拓扑优化模型，进行拓扑优化计算，经过86次迭代计算后，计算结果收敛，拓扑优化计算结束。

质量分数（MF）表示各个部件质量与初始质量之比，在10步前，曲线斜率较陡，并在第9步达到设定的目标质量分数，如图13所示。图中，P2_MassFrac和P6_MassFrac为泄压门质量分数随迭代步的变化过程，P4_MassFrac和P5_MassFrac为铰链质量分数随迭代步的变化过程。

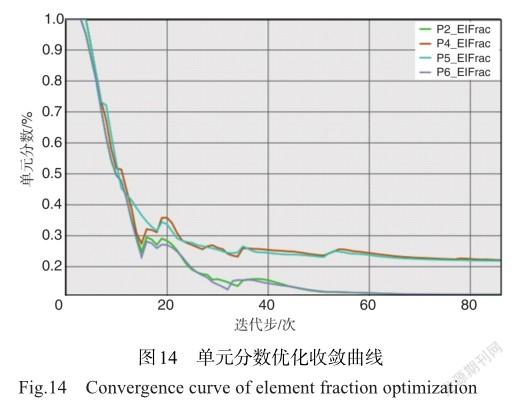
单元分数（EF）表示各个部件剩余单元与初始单元数量之比，单元分数随迭代步变化如图14所示，图中P2_ElFrac和P6_ElFrac为泄压门单元分数随迭代步的变化过程，P4_ElFrac和P5_ElFrac为铰链单元分数随迭代步的变化过程。38迭代步前，单元分数曲线斜率较大，说明拓扑布局变化较大，优化效率较高，38步之后曲线平缓逐渐收敛。第86步优化收敛后，得到的单元密度分布云图如图15所示。泄压门上加筋从铰链与连接点处呈树状向外延伸，同时加筋高度逐渐降低最终与泄压门融合。

2.5泄压门铰链结构拓扑优化结果几何模型重构

从优化结果中按密度分布云图等值面提取得到拓扑优化后的泄压门筋条模型，此模型为三角面片组成的离散模型，如图16所示。

对该模型三角面片进行修整、光顺，利用几何建模工具对面片进行拟合和拼接，形成由多组非均匀有理样条曲面（NURBS）组成的壳体，如图17所示。

在UG中，对壳体模型进行填充得到图18所示的最终泄压门拓扑优化几何模型，可用于后续的3D打印。

2.6泄压门优化前后关键参数及损伤形式对比

采用显式动力学流固耦合算法，对泄压门优化前后构型在航空发动机短舱腔压产生的气动力作用下的展开过程进行仿真，仿真结果如图19所示，泄压门铰链优化后峰值应力从337MPa降为301MPa，泄压门盖板通过优化后的加强筋结构加强，使其中部弯折塑性变形得到明显改善。

2.7泄压门拓扑优化构型3D打印试验件试制

采用3D打印技术加工泄压门拓扑优化构型，如图20所示，采用与原方案一致的铝合金材料，验证了优化构型的可实现性。

3结论

本文针对一种拓扑最优化的新方法——基于局部控制规则的HCA算法，对其进行工程应用方法研究。对于考虑材料失效工况下应力约束和位移约束的结构拓扑优化问题，在传统HCA方法基础上引入材料失效判据。

算例优化结果表明，该方法对于冲击动力学载荷工况、约束和各向同性的均质材料结构的优化设计，对结构失效进行优化是有效、可行的。同时，也说明HCA理论和方法具有工程应用价值。

从工程应用角度考虑，还需要对优化效果进行试验验证，用航空发动机强度设计准则证明优化结果的设计符合性。

参考文献

[1]庄来杰，丁小飞，马斯博，等.涡轮后机匣支点弹性支承结构优化研究[J].航空科学技术， 2019， 30（10）：45-48. Zhuang Laijie， Ding Xiaofei， Ma Sibo， et al. Study on Optimization of elastic support structure of turbine rear casing fulcrum[J]. Aeronautical Science&Technology， 2019， 30（10）： 45-48. （in Chinese）

[2]吕佩.提高航空工业技术创新层次与水平的思考[J].航空科学技术， 1996，8（6）：6-8. Lyu Pei. Thoughts on improving the level and level of technological innovation in aviation industry[J]. Aeronautical Science & Technology， 1996，8（6）： 6-8. （in Chinese）

[3]何旅洋，郑百林，杨彪，等.航空发动机叶片抗冲击动力学拓扑优化研究[J].力学季刊， 2016， 37（3）：513-521. He Lyuyang， Zheng Bailin， Yang Biao， et al. Study on topological optimization of impact resistance dynamics of aeroengine blades[J]. Chinese Quarterly of Mechanics， 2016， 37（3）： 513-521. （in Chinese）

[4]张声伟.运输机机翼平面参数快速优化方法[J].航空科学技术， 2014，25（9）：15-18. ZhangShengwei.Fastoptimizationmethodofplane parameters of transport aircraft wing[J]. Aeronautical Science& Technology， 2014，25（9）： 15-18. （in Chinese）

[5]杜鵬良，谭申刚，李明强.机身大开口刚度补强设计及优化[J].航空科学技术， 2016， 27（4）：16-20. DuPengliang， TanShengang，LiMingqiang.Stiffness reinforcement design and optimization of fuselage with large opening[J]. Aeronautical Science & Technology， 2016， 27（4）： 16-20. （in Chinese）

[6]王安麟，姜涛.基于进化元胞自动机的结构拓扑优化[J].机械工程学报， 2005， 41（2）：1-5. Wang Anlin， Jiang Tao. Structural topology optimization based on evolutionary cellular automata[J]. Journal of Mechanical Engineering， 2005， 41（2）： 1-5. （in Chinese）

[7]葛锐，陈建桥，魏俊红.基于改进粒子群优化算法的复合材料可靠性优化设计[J].机械科学与技术， 2007， 26（2）：257-260. Ge Rui， Chen Jianqiao， Wei Junhong. Reliability optimal design of composite materials based on the improved particle swarm optimization algorithm[J]. Mechanical Science and Technology for Aerospace Engineering， 2007， 26（2）： 257-260.（in Chinese）

[8]沈亚栋，封建湖，王勋涛，等.基于混合元胞自动机法的结构可靠性拓扑优化[J].机械强度， 2018， 40（6）：74-81. Shen Yadong， Feng Jianhu， Wang Xuntao， et al. Structural reliability topology optimization based on hybrid cellular automata[J]. Journal of Mechanical Strength， 2018， 40（6）：74-81. （in Chinese）

[9]隋允康，叶红玲，彭细荣.应力约束全局化策略下的连续体结构拓扑优化[J].力学学报， 2006（3）：364-370. SuiYunkang，YeHongling，PengXirong.Topology optimization of continuum structure under stress constraint global strategy[J]. Chinese Journal of Theoretical and Applied Mechanics， 2006（3）： 364-370. （in Chinese）

[10]荣见华，葛森，邓果，等.基于位移和应力灵敏度的结构拓扑优化设计[J].力学学报， 2009， 41（4）：518-529. Rong Jianhua， Ge Sen， Deng Guo， et al. Structural topology optimizationdesignbasedondisplacementandstress sensitivity[J]. Chinese Journal of Theoretical and Applied Mechanics， 2009， 41 （4）： 518-529. （in Chinese）

[11]王冠，張骞，寇琳媛，等.基于混合元胞自动机算法的连续体结构非线性拓扑优化[J].中国机械工程， 2020，31（18）：2161-2173. Wang Guan， Zhang Qian， Kou Linyuan， et al. Nonlinear topology optimization of continuum structure based on hybrid cellular automata algorithm[J]. China Mechanical Engineering， 2020， 31 （18）： 2161-2173. （in Chinese）

[12]周珍珍.基于混合元胞自动机方法的结构拓扑优化研究[D].武汉：华中科技大学，2009. Zhou Zhenzhen. Research on structural topology optimization based on hybrid cellular automata[D]. Wuhan： Huazhong University of Science and Technology， 2009. （in Chinese）

[13]田启华，向晓波，王进学.基于HCA的拓扑优化状态场变量更新技术[J].机械设计与研究， 2014， 30（3）：18-21. TianQihua，XiangXiaobo，WangJinxue.Topology optimization state field variable updating technology based on HCA[J]. Machine Design & Research， 2014， 30 （3）： 18-21. （in Chinese）

Research on Topology Optimization Technology of Shock Loading Structure of Aeroengine Nacelle Relief Valve

Hou Liang1，Chai Xianghai1，Bai Guojuan1，Jin Zhixian2

1. AECC Commercial Aircraft Engine Co.，Ltd.，Shanghai 200241，China

2. Zhejiang University，Hangzhou 310027，China

Abstract： The working load type of some aeroengine parts belongs to impact load. The design conformity cannot be proved by the criterion of static strength judgment， which leads to the failure of structural optimization by static load. Therefore， it is necessary to establish a topological optimization method of aeroengine structure based on impact dynamic load. Taking the hinge of the pressure relief valve of aeroengine as the research object， the topological optimization method of the pressure relief valve under the action of the spring open load caused by the pressure in the cabin cavity is established by the topological optimization technology of the structural impact dynamic load， which improves the hinge strength margin of the pressure relief valve and solves the hinge fracture problem in the strength test of the pressure relief valve. The topology optimization method of aeroengine structure based on impact dynamic load can avoid the error of dynamic equivalent static load， and the optimization results are more in line with the load transmission characteristics， which provides an effective solution for the optimization of weight reduction and stress reduction of aeroengine components.

Key Words： aeroengine； topology optimization； impact dynamics； stress； weight loss

3799500338257