改进MDSMOTE与PSO-SVM在汽车组合仪表分类预测中的应用

肖 圳，何 彦，李育锋，吴鹏程，刘德高，杜 江

（1.重庆大学机械传动国家重点实验室，重庆 400030；2.重庆矢崎仪表有限公司，重庆 401123）

随着制造技术的不断改进，现代先进制造业正朝着高精度、高效率以及智能化的方向发展［1-2］。在当前的电子产品制造过程中，智能化转型升级使得原有的大规模生产模式转变成了多品种、小批量的生产模式［3］。为了满足汽车用户多样的个性化需求，汽车组合仪表制造企业不得不面对仪表种类增加、订单调整频繁及工艺参数多变等一系列挑战，亟须进一步提升生产效率。

鉴于汽车组合仪表在保证驾驶安全中具有重要作用，对缺陷仪表进行准确筛选始终是制造企业关注的重点。因此，各制造企业在汽车组合仪表的生产过程中设置了众多质检项目，使得检测时间变长，这在一定程度上制约了生产效率的提升。

为了改善传统的产品质量控制过程，常采用传感器与分布式控制系统（distributed control system，DCS）来获取海量的生产数据，并通过这些易测量的过程变量来构建预测模型［4］。例如：陈鑫等［5］选取关键工序历史质量数据，通过贝叶斯理论建模实现了柴油机喷油孔镗削工序的质量控制；吴双等［6］结合反向传播（back propagation，BP）神经网络和极限梯度提升（extreme gradient boosting，XGBoost）算法建立了产品质量预测控制模型，并将其应用于薄膜晶体管液晶显示屏的质量分类，为其加工过程的优化提供了可靠参考。

由于在实际生产过程中，合格产品占绝大多数，而缺陷产品数量较少，产品质量数据呈现出类别极不平衡的特点，常规的机器学习预测模型难以对其进行准确分类。针对生产数据不平衡的产品分类问题，大量研究集中于数据预处理、特征选择和分类算法三个方面［7］。例如：张鑫等［8］基于拉普拉斯特征映射改善了机械设备故障标签样本不足的问题；Khan等［9］提出一种基于代价敏感学习的深度神经网络，用于自动学习多数和少数类别的鲁棒特征表示；杨浩等［10］将Boosting算法应用于代价敏感学习，建立了基于近邻样本间距的K最近邻分类模型。但是汽车组合仪表生产数据具有的高维特性可能会导致特征选择过程存在信息丢失的问题，从而对最终的分类精度产生不利影响；而以代价敏感学习为主的分类算法由于缺少准确、统一的错分代价估计方法，难以保证分类预测模型的泛化性。因此，在汽车组合仪表的分类中，基于重采样的数据预处理方法得到了广泛应用。

重采样包括欠采样和过采样方法。相比于欠采样方法要舍弃部分产品质量数据，过采样方法不仅能够保留所有原始生产数据的信息，还可通过增加少量缺陷产品的数量来改善分类效果。Chawla等［11］提出了经典的合成少数类过采样技术（synthetic minority over-sampling technique，SMOTE），通过在少数类样本中线性插值来随机生成新的数据，降低了简单重复过采样带来的过拟合风险。Han等［12］提出了Borderline-SMOTE，通过在种类边缘数据中插值来避免经典SMOTE易生成噪声数据的问题。罗康洋等［13］提出了一种SMOTE与混合核支持向量机（support vector machine，SVM）相结合的迭代算法，利用较少的迭代采样次数来改善数据的不均衡性。张忠林等［14］提出了一种基于SVM的过采样方法，根据少数类样本到分隔超平面的距离赋予权重，经多次迭代合成新样本以满足SVM的运算需求。刘云鹏等［15］制定了不同的决策机制，通过SMOTE对分类边界上的支持向量进行插值，提高了变压器故障诊断精度。

目前，针对不平衡生产数据的过采样方法主要侧重于多次迭代或插值，但这些方法改变了原始数据的分类边界，无法完全反映产品的实际分类情况，且会使分类预测模型的复杂程度增加及运算时间变长。为此，笔者提出一种基于改进最远点SMOTE（max distance SMOTE，MDSMOTE）的SVM分类预测方法，旨在对汽车组合仪表生产过程进行准确的质量控制。针对获取的汽车组合仪表贴片、组装等生产过程的数据，结合专家经验筛选与仪表质量相关的工序数据并将其作为分类预测模型的输入。首先，运用改进MDSMOTE对少数类缺陷汽车组合仪表的生产数据进行插值处理，保证预测模型得到的分类边界更加贴近实际；然后，建立基于粒子群优化（particle swarm optimization，PSO）算法优化参数的SVM分类预测模型；最后将优化后的SVM分类预测模型应用于汽车组合仪表的分类预测，以改善其质量控制过程，提高整体生产效率。

1 数据过采样方法

1.1 SMOTE

SMOTE通过人工合成少数类样本来改善各类样本间的不平衡性。针对任意r维样本Xp=（xp1，xp2，…，xpr）和Xq=（xq1，xq2，…，xqr），其欧氏距离Dpq为：

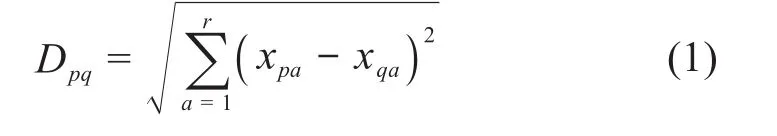
基于过采样倍率为N，在每个少数类样本Xp的M个同类最近邻样本中随机选择N个样本。根据聚类思想可知，与正类样本在空间上距离较近的样本也为正类［16］。利用SMOTE对N个近邻样本中的每一个样本Xq（q=1，2，…，N）按照式（2）在其与少数类样本Xp的连线上进行插值以获取新样本，遍历所有少数类样本后形成类别平衡的数据集。

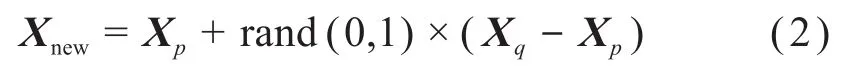
式中：Xnew为新生成的样本；rand（0，1）为0～1之间的任一随机数。

1.2 改进MDSMOTE

由于SMOTE是在少数类样本的邻域中随机生成新样本，增大了各类样本在分类边界处的重叠程度，并显著提高了处理较高维度数据时的计算复杂程度。而MDSMOTE仅针对少数类样本的质心及距离质心最远的少数类样本，在二者的连线上随机生成新样本，大幅减少了运算次数。但是MDSMOTE将新样本的生成区域限制在特征空间内部的一条直线上，针对数据量较大且类不平衡率较高的数据集，生成的新数据集分布过于集中，导致训练得到的预测模型难以反映实际产品的分类情况。

针对上述不足，提出改进的MDSMOTE，以改善新生成样本的分布情况。以二维样本为例，其原理如图1所示，即通过引入类不平衡率IR对少数类样本进行插值处理，具体方法如下：

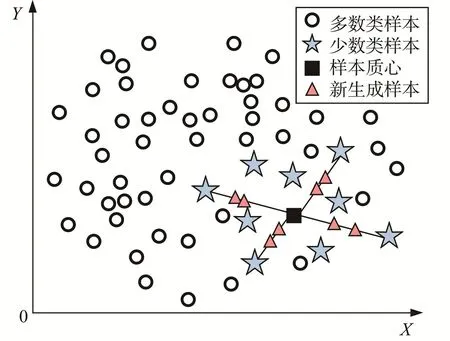
图1 改进MDSMOTE的原理Fig.1 Principle of improved MDSMOTE

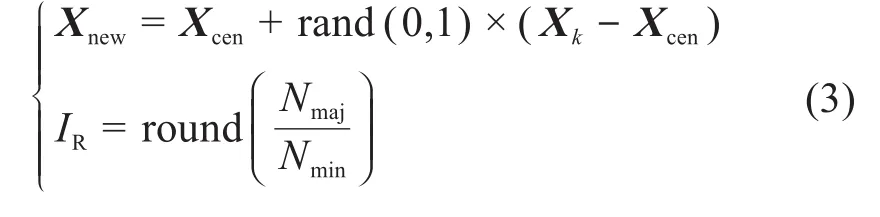
式中：Xcen为所有少数类样本的质心；Nmaj、Nmin分别为多数类和少数类样本的数量；round（）为四舍五入取整函数；Xk为第k个距离质心最远的少数类样本，k=1，2，…，IR。

改进MDSMOTE的具体步骤如下：

1）对任一输入样本集X，通过计算得到少数类样本的质心Xcen，并遍历少数类样本确定距离质心最远的 IR个样本 Xk。

2）利用式（3）分别在质心Xcen与IR个最远样本Xk的每条连线上随机生成新的少数类样本Xnew，从而达到平衡原始数据集的目的。

改进MDSMOTE仅迭代IR次，可降低数据预处理过程的复杂程度，同时在不改变原始分类边界的情况下使数据分布得更加均匀，从而提高人工合成少数类样本的质量。

2 SVM及其参数优化

2.1 SVM

SVM以统计学习理论为基础，是一种适用于小样本、泛化能力强的监督学习算法。SVM通过非线性映射将样本空间映射到更高维的特征空间中，找到分隔正、负样本的最佳超平面，保证2种类型的样本到分隔超平面的距离总和最大，其具备优良的分类性能。

式中：Xi为输入向量，Xi∈ Rn；yi为对应的标签数据，yi∈｛-1，1｝；ω为分隔超平面权重矢量；b为偏差量；ξi为非负的松弛变量；C为惩罚因子；φ()为非线性映射函数，可将样本数据映射到更高维的特征空间中，避免了原始数据线性不可分的问题。

构建上述方程（4）的拉格朗日函数，根据Karush-Kuhn-Tucker（KKT）条件，对ω和b求偏导并作置零处理，从而求解得到最优判别函数，表示为：

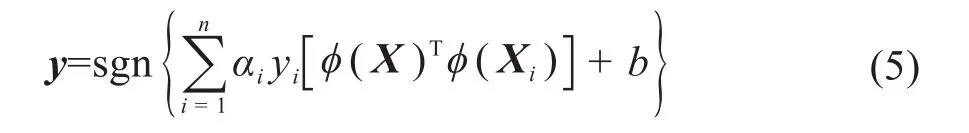
式中：αi(i=1，2，…，n)为引入的拉格朗日乘子。

定义SVM的核函数K（Xi，Xj）=φ（Xi）Tφ（Xj）。SVM常用的核函数主要有线性核函数、多项式核函数、径向基函数（radialbasisfunction，RBF）和sigmoid核函数等。鉴于RBF的参数较少，对预测模型复杂程度的影响小，且具有较宽的收敛域和较强的泛化能力［17］，本文选择RBF作为SVM的核函数，其表达式如下：

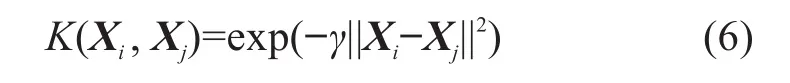
式中：γ为核函数参数。

2.2 基于PSO的SVM参数优化

对于以RBF为核函数的SVM分类预测模型，误差惩罚因子C和核函数参数γ是影响其预测精度的重要参数。为了提高汽车组合仪表分类的准确率，须对C和γ的取值进行优化。

PSO在动态目标寻优方面具有收敛速度快、搜索机制简单和鲁棒性好等优点，可有效避免陷入局部最优解的情况［18］。PSO对参数进行更新的方法如下：

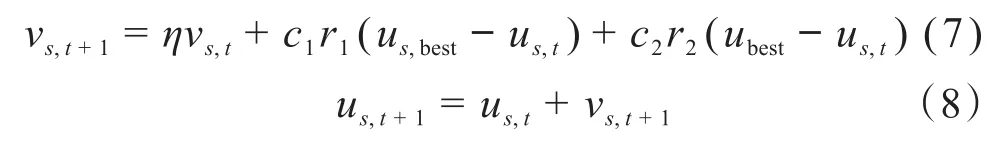
式中：us为搜索空间中第s个粒子的位置；νs为第s个粒子的运动速度；t为当前更新次数；η为惯性权重；c1、c2为加速系数；r1、r2为0～1之间的随机数；us，best为第s个粒子目前搜索到的最优位置；ubest为目前搜索到的全局最优位置。

综上，基于改进MDSMOTE和PSO-SVM的汽车组合仪表分类预测流程如图2所示。

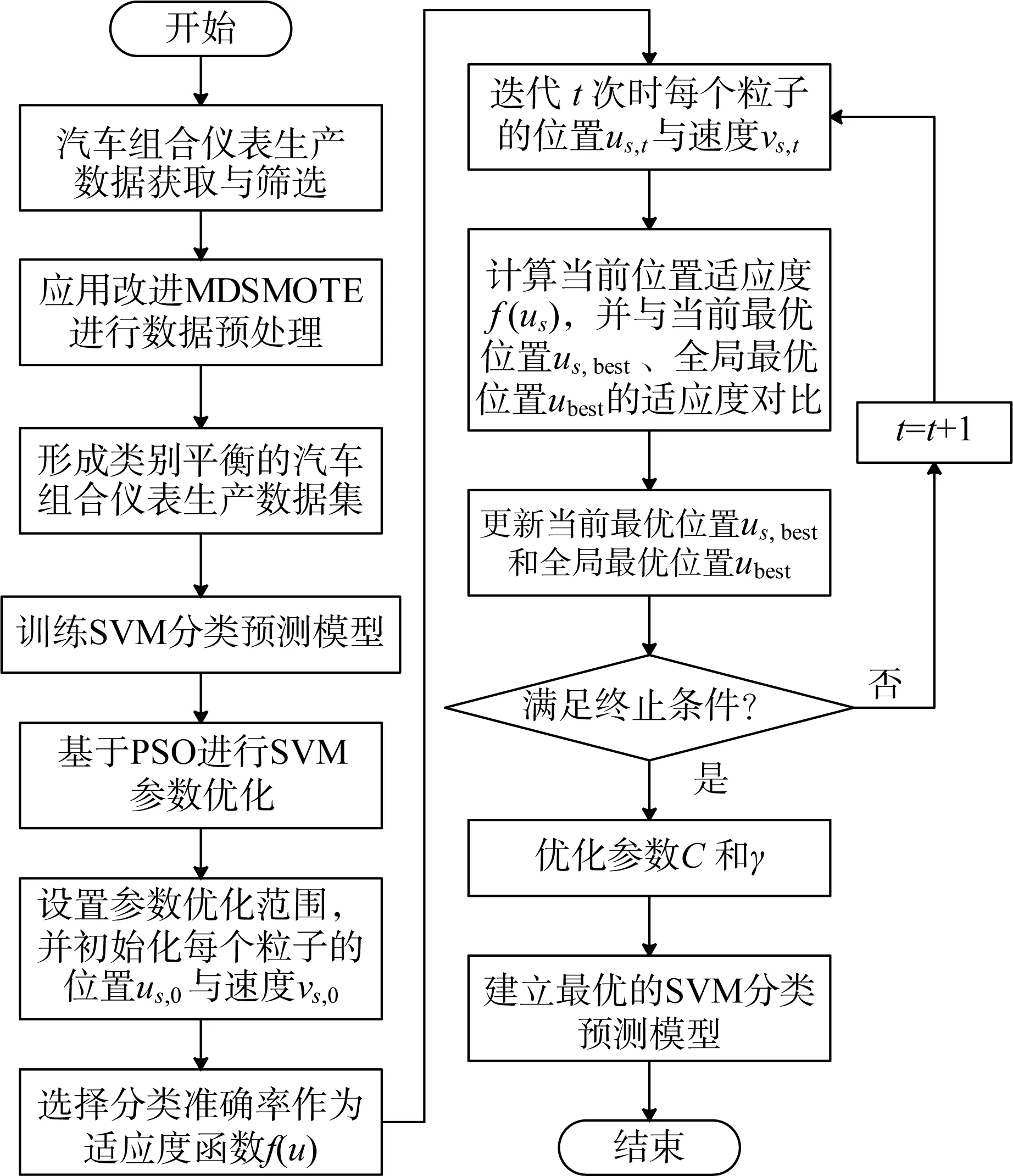
图2 基于改进MDSMOTE和PSO-SVM的汽车组合仪表分类预测流程Fig.2 Classification and prediction process of automobile combination instrument based on improved MDSMOTE and PSO-SVM

由图2可知，基于改进MDSMOTE和PSO-SVM的汽车组合仪表分类预测流程具体如下：

1）结合专家经验对获取的汽车组合仪表生产数据进行筛选。

2）应用改进MDSMOTE对筛选后的数据进行预处理，形成类别平衡的汽车组合仪表生产数据集，以用于训练SVM分类预测模型。

3）应用PSO算法对SVM的误差惩罚因子C和核函数参数γ进行优化，并设置粒子的初始位置us，0和初始速度νs，0，种群规模为m，搜索空间为2维。

4）以汽车组合仪表分类准确率作为适应度函数f（u）。

5）利用式（7）和式（8）对粒子的位置与速度进行更新，得到迭代 t次的粒子位置 us，t与速度 νs，t。

6）计算当前位置的适应度f（us），并与当前最优位置的适应度f（us，best）进行对比，若f（us）＞f（us，best），则更新当前最优位置 us，best=us，t；同理对全局最优位置 ubest进行更新。

7）若不能满足终止条件，则返回步骤5）继续迭代；若满足则停止迭代，输出优化的参数C和γ，建立最优的SVM分类预测模型。

3 汽车组合仪表分类预测实例

3.1 汽车组合仪表生产数据获取

为了测试所提出的基于改进MDSMOTE和PSO-SVM的分类预测方法的性能，以重庆某仪表制造企业的汽车组合仪表生产过程为例，选取不同种类仪表在不同批次的生产情况进行验证。典型的汽车组合仪表主要由车速表、转速表和印刷电路板（printed circuit board，PCB）组件构成，如图3所示。

图3 典型汽车组合仪表的内部结构Fig.3 Internal structure of typical automobile combination instrument

汽车组合仪表的生产过程主要包括PCB表面贴片和元器件组装这2个环节，具体流程如图4所示。为了进行可追溯的汽车组合仪表质量控制，采用Hitachi MS710印刷机、CKD VP5200L-V锡膏检查设备、压力传感器和红外距离传感器等设备获取各工序的实时生产数据。

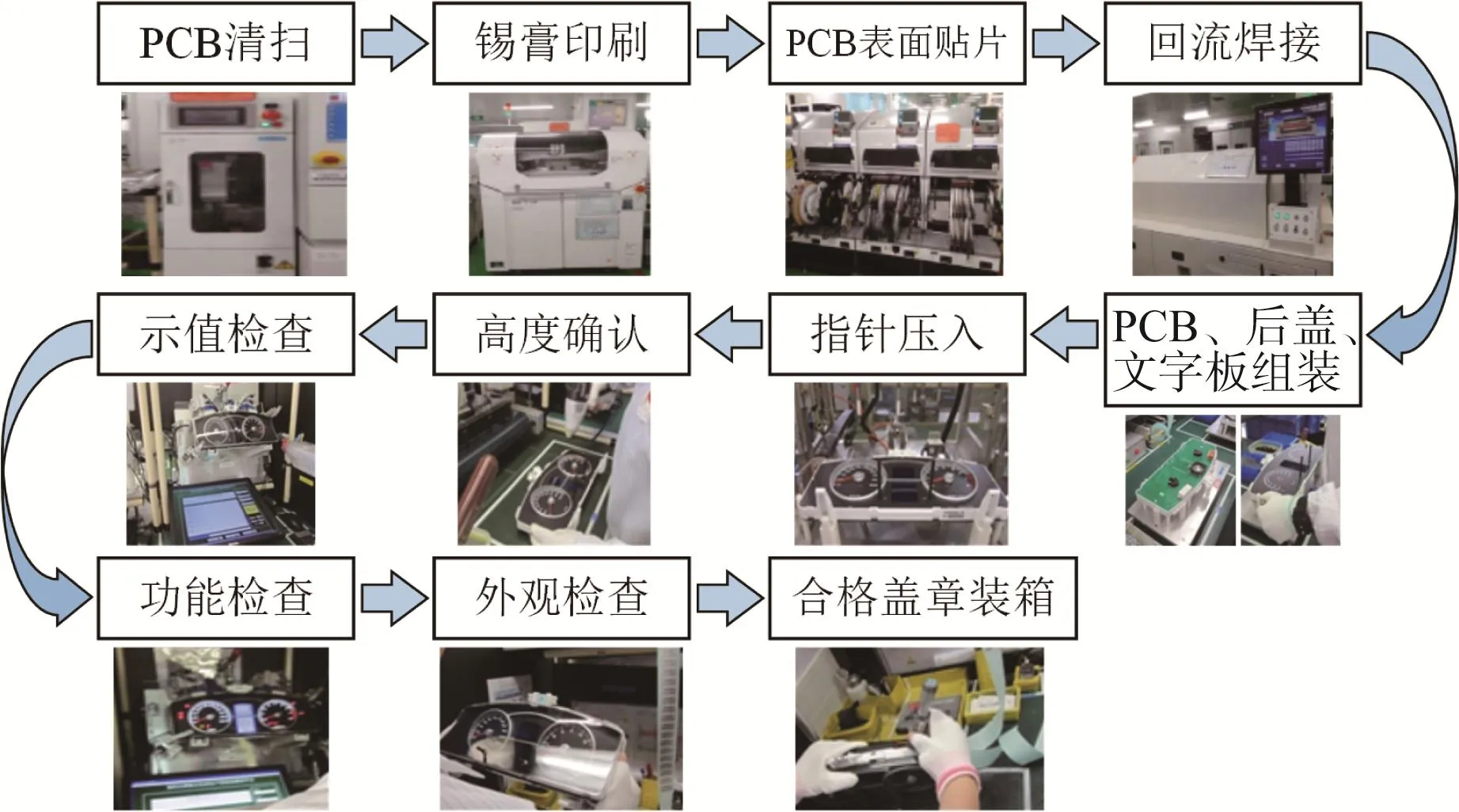
图4 汽车组合仪表生产流程Fig.4 Production process of automobile combination instrument

由于输入数据的质量会直接影响分类预测模型的精度，须对生产数据进行特征筛选［19］。结合专家经验与汽车组合仪表的生产工艺，选择涉及仪表指示功能的锡膏印刷、指针压入和高度确认等工序的生产数据作为分类预测模型的输入，忽略贴片、组装等非功能性工序对仪表质量的影响。筛选后的汽车组合仪表生产数据如表1所示。

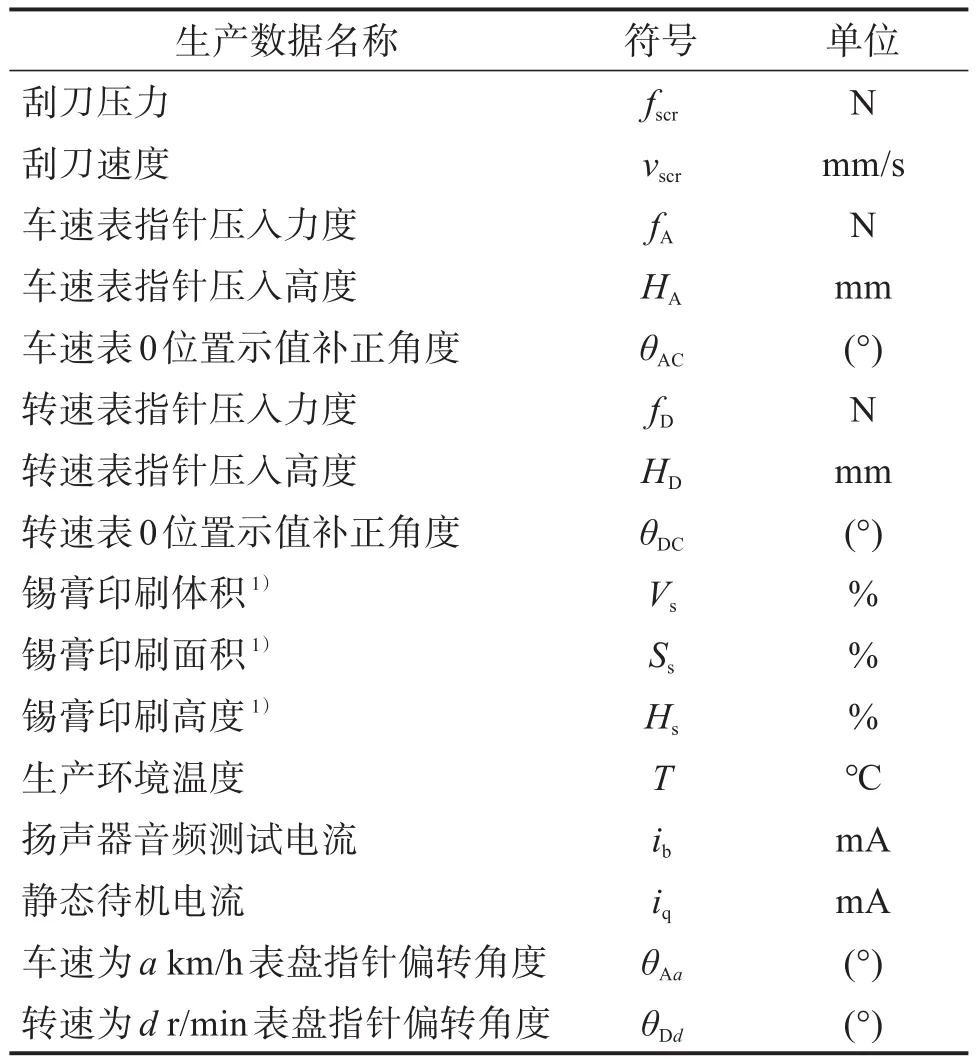
表1 筛选后的汽车组合仪表生产数据Table 1 Screened production data of automobile combination instrument

本文选择3种不同类型的汽车组合仪表的各2个批次的生产数据来构建数据集，其详细情况如表2所示。随机选择每组数据的80%作为训练集，用于分类预测模型的训练；其余20%作为测试集，用于评估分类预测模型的性能。

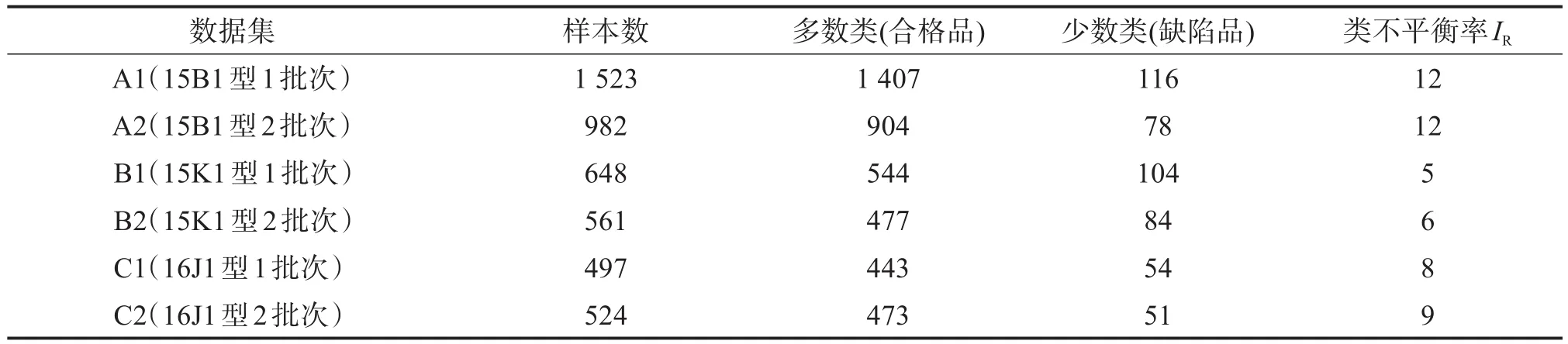
表2 汽车组合仪表生产数据集详细情况Table 2 Production data set details of automobile combination instrument

在各工序上采集的生产数据的数量级存在差异，为了提高分类预测模型的准确率和泛化能力，对原始数据进行归一化处理：

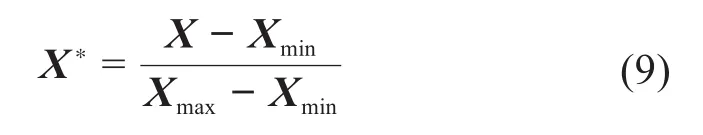
式中：X*为归一化处理后的数据；X为原始生产数据；Xmin、Xmax分别为原始生产数据的最小值和最大值。

3.2 分类效果评价指标

引入混淆矩阵来评价分类预测模型的性能，定义少数类的缺陷产品为正值，多数类的合格产品为负值，如表3所示。

表3 汽车组合仪表分类混淆矩阵Table 3 Confusion matrix of automobile combination instrument classification

通常采用准确率A作为模型性能的评价指标，其表达式如下：

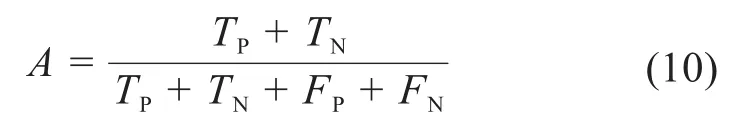
针对不平衡数据集，由于某一类样本数量较少，使得整个数据集的分类准确率不足以对预测结果进行全面、有效的评价。因此，本文采用反映分类预测模型在缺陷产品中的分类精确程度的查准率P、衡量分类预测模型对缺陷产品的整体识别能力的查全率R、整体考虑查准率和查全率影响的F值Fβ以及综合考虑对正、负样本分类准确率的几何平均值Gmean对所构建的分类预测模型进行评价［13］。

各评价指标的表达式如下：

式中：β为查全率与查准率的比值，本文取β=1（即Fβ=F1），表示查准率和查全率同样重要。

3.3 分类结果对比分析

为了验证基于改进MDSMOTE的PSO-SVM分类预测方法的有效性与优越性，应用Borderline-SMOTE［12］、MDSMOTE［16］和改进 MDSMOTE 对不同的汽车组合仪表测试集进行数据处理，并对比其分类性能。

利用Python语言编写过采样方法的运行程序，并使用scikit-learn库搭建SVM分类预测模型。在利用PSO算法对SVM分类预测模型的参数进行优化时，设置种群规模为20，空间维度为2，最大迭代次数为100。基于不同模型的汽车组合仪表分类预测结果如表4所示。在不同数据集上各模型的分类准确率、F值和几何平均值对比曲线如图5至图7所示，其中横坐标中的数据集按类不平衡率从小到大排序。

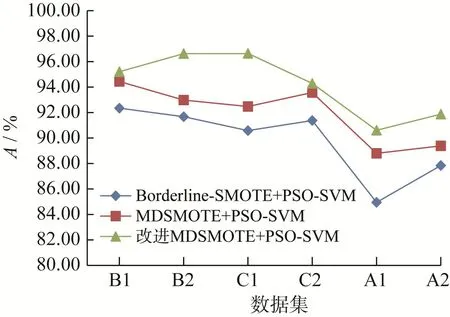
图5 不同分类预测模型的准确率对比Fig.5 Comparison of accuracy of different classification prediction models

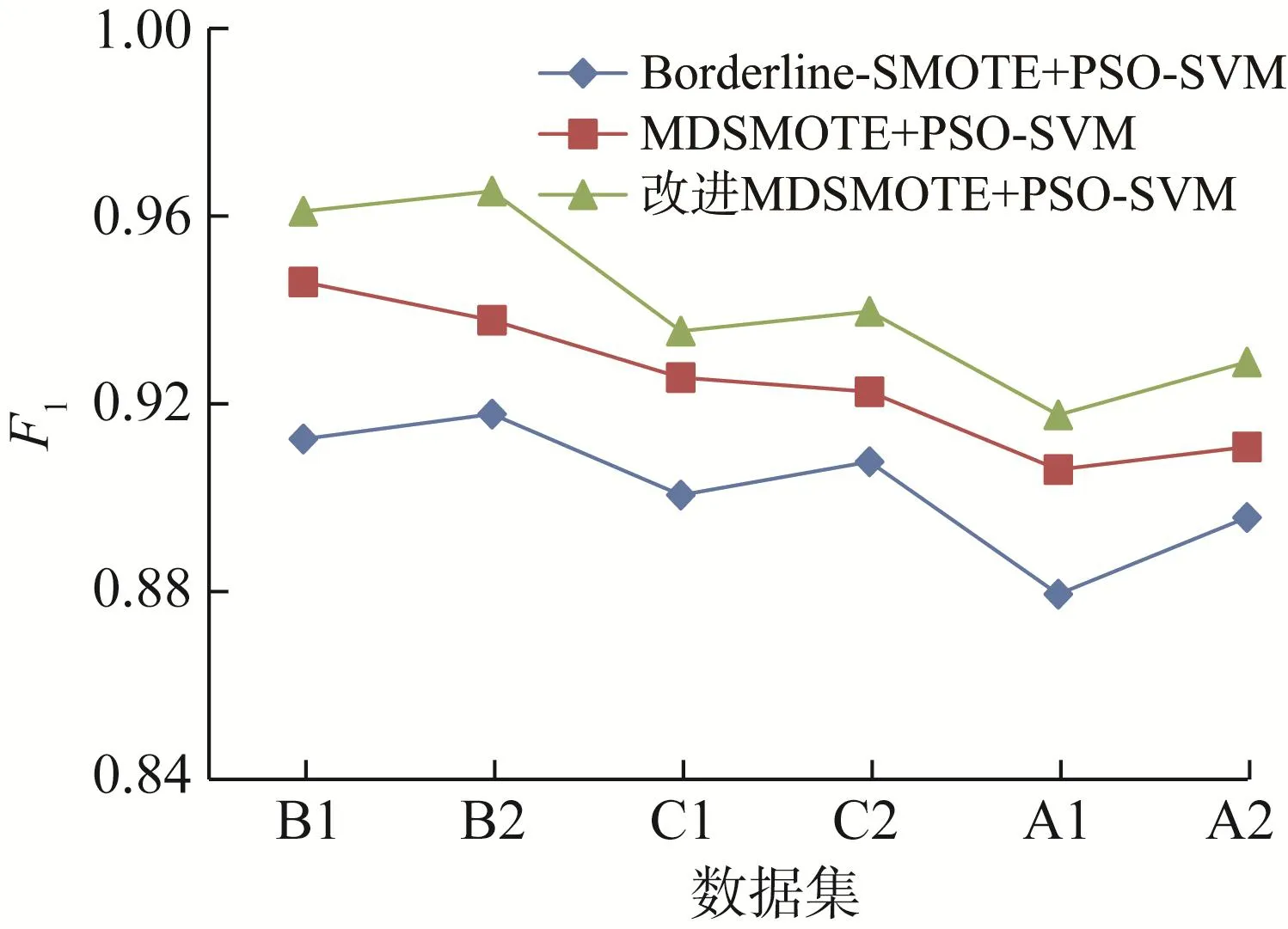
图6 不同分类预测模型的F值对比Fig.6 Comparison of F value of different classification prediction models

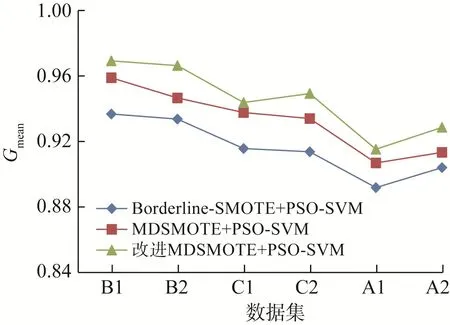
图7 不同分类预测模型的几何平均值对比Fig.7 Comparison of geometric mean value of different classification prediction models

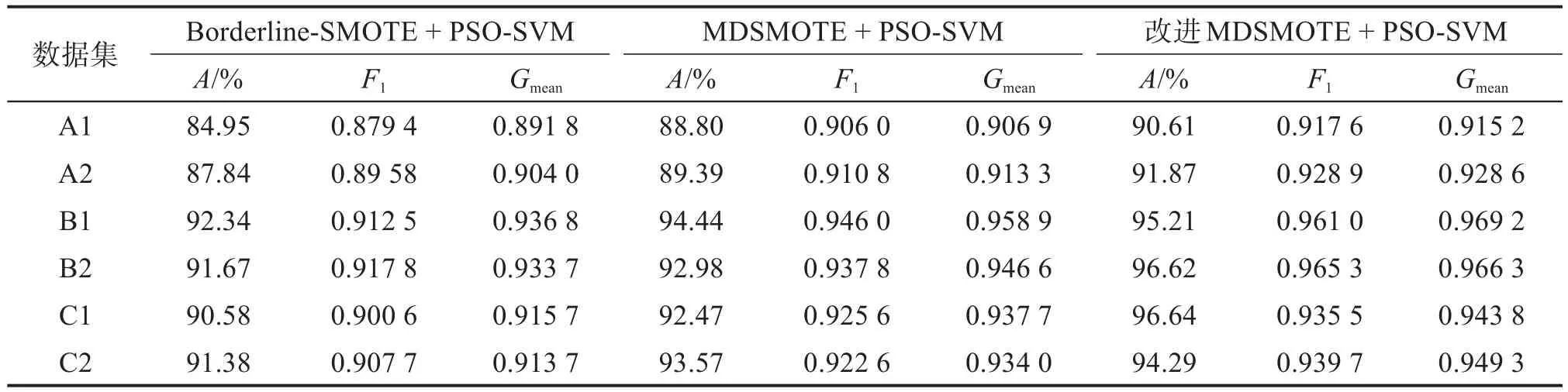
表4 基于不同模型的汽车组合仪表分类预测结果Table 4 Classification prediction results of automobile combination instrument based on different models

从表4中可以看出，基于改进MDSMOTE的PSO-SVM分类预测模型在汽车组合仪表分类预测中的效果较好。

在准确率方面，基于Borderline-SMOTE的PSO-SVM分类预测模型的准确率较低，基于MDSMOTE的PSO-SVM分类预测模型居中，基于改进MDSMOTE的PSO-SVM分类预测模型最高，且在数据集B2和C1中超过了96.00%，与其他2个分类预测模型相比，其准确率平均提高了4.94%和2.47%。但是各分类预测模型在类不平衡率较大的数据集上的准确率普遍低于类不平衡率较小的数据集。

在分类预测效果方面，基于改进MDSMOTE的PSO-SVM分类预测模型同样表现最佳，相比于其他2个分类预测模型，其F值分别提高了4.32%和1.79%，几何平均值分别提高了3.21%和1.34%，说明该模型的整体分类性能得到了提升。从提升程度上看，基于改进MDSMOTE的PSO-SVM分类预测模型相较于基于Borderline-SMOTE的提升程度更大，这是因为后者是在少数类样本边界上进行了数据扩充，使得模型分类难度增大，前者则针对少数类样本的中心数据进行过采样方法的优化，没有改变边界数据分布情况，因此分类性能得到显著提升。

综上可得：

1）在缺陷汽车组合仪表的筛选上，基于改进MDSMOTE的PSO-SVM分类预测模型的准确率、F值和几何平均值最高，即分类效果最好，相比于基于MDSMOTE的PSO-SVM分类预测模型，其分类性能小幅度提升，而相比于基于Borderline-SMOTE的PSO-SVM分类预测模型，其分类性能的提升程度更高。这主要是因为MDSMOTE及其改进方法采用中心化思想，生成的新样本均在特征空间内部，对分类边界上的支持向量影响较小；而Borderline-SMOTE增大了边界数据的重叠程度，不易获得清晰的分类边界，导致应用该方法的分类预测模型的性能仍存在提升空间。

2）随着数据集类不平衡率的增大，各分类预测模型的性能均出现了明显下滑。类不平衡率较大表示缺陷仪表的占比较小（如A1和A2），因此需要在特征空间内人工生成更多的正值样本，以满足SVM的训练需求。这使得Borderline-SMOTE和MDSMOTE在分类边界处生成的样本数量增加，增大了对分类性能的负面影响，而改进MDSMOTE因具有较强的泛化能力，随着类不平衡率的增大，其所生成的新样本较分散，对分类边界的影响较小，即其泛化能力较强。

3）对于类不平衡率相当的数据集，各分类预测模型在样本数量较少的数据集（如A2）上均取得了更高的准确率、F值和几何平均值，这进一步验证了SVM在小样本分类问题上的优越性。当样本数量无较大差别（如B1和 B2、C1和C2）时，基于改进MDSMOTE的PSO-SVM分类预测模型的F值和几何平均值的变化不明显，而基于其他方法的分类预测模型的波动则相对较大，说明本文模型的分类性能更加稳定，对缺陷仪表的筛选结果更为可靠。

4 结 论

本文针对缺陷汽车组合仪表的筛选问题，提出了一种基于改进MDSMOTE的PSO-SVM分类预测方法，用于仪表生产过程的质量控制。通过在MDSMOTE中引入类不平衡率来对生成的新样本进行改善，使得新数据集分布得更加均匀。并利用PSO算法对SVM分类预测模型的参数进行优化，以提升模型的分类预测性能。通过与其他分类预测模型在不同的数据集上的分类结果进行对比可知，基于改进MDSMOTE的分类预测模型在准确率、分类效果方面均取得了不同程度的提升，其分类性能优良，同时具有较强的泛化能力和稳定性，为仪表制造企业生产效率的提升提供了有效指导。

然而，基于改进MDSMOTE的PSO-SVM分类预测模型在类不平衡率较大的数据集上的分类性能仍有待提升，后续研究将对比其他分类预测模型和不同的启发式参数优化方法，以期建立更优的模型，并降低参数寻优复杂程度。