轮腿式爬壁机器人的永磁吸附装置设计与优化

钟道方，田 颖，张明路

（河北工业大学机械工程学院，天津 300401）

石油化工储罐和船舶均为大型金属立面结构。针对此类立面的除锈、喷漆和检测等维护作业［1-2］，国内外学者研制了多种爬壁机器人，辅以相应的先进作业工艺，利用它们代替人工来完成上述高危作业［3-4］。爬壁机器人的吸附能力是其在大型立面上灵活运动及越障的基础。目前，大型爬壁机器人的吸附方式主要有负压吸附和永磁吸附两种。其中：负压吸附具有受限于能耗、噪音大和功率小的缺点，不适用于大负载作业情况［5］；而永磁吸附具有可靠性高、能耗低和结构简单的优点，相比于负压吸附，其为爬壁机器人较常采用的吸附方式［6］。

Tavakoli、宋伟等［7-8］所研制的爬壁机器人的磁吸附装置安装在车轮上，其可提供一定的磁吸附力来承受机器人整体的重量。Nagaya、崔宗伟等［9-10］设计的检测爬壁机器人采用分体式移动机构与磁吸附装置相结合的方式，能够在类似于单一曲面的立面上进行爬壁运动。Xu等［11］通过集轮式运动和永磁吸附于一体，研制了用于船舶除锈的喷砂爬壁机器人，同时利用加载实验验证了该机器人的车轮能够承受120 kg的有效载荷。闫晨飞等［12-13］基于永磁吸附技术研制了一种变磁化方向单元组合式永磁吸附装置，其可增强爬壁机器人的吸附能力。赵军友等［14］研究了爬壁机器人磁吸附单元的尺寸参数与其磁吸附力的关系，并在此基础上设计并优化了其辅助吸盘的尺寸参数，以保证机器人可稳定地吸附在油罐壁面上。但是，上述爬壁机器人均采用履带或轮式移动方式，由于这些移动方式多采用车轮与磁吸附装置相结合的模式，使得机器人无法翻越较高的障碍，限制了其应用场合。

针对常见爬壁机器人越障能力较弱的问题，笔者以轮腿式爬壁机器人为研究对象，结合其越障原理以及永磁吸附原理，设计了一种基于非接触式永磁吸附单元磁极交叉的线性阵列结构，即非接触式永磁吸附装置。通过有限元仿真对该永磁吸附装置的磁感应强度和磁吸附力进行分析计算，并分析不同结构参数对其磁吸附力的影响，旨在为轮腿式爬壁机器人磁吸附装置的设计与优化奠定基础。

1 永磁吸附装置设计

永磁吸附是基于磁通的连续性原理及磁场的叠加原理实现的。本文将永磁吸附的磁路设计成多个磁系，通过不同磁极（N极与S极）的交叉设计来实现工作磁极面上连续磁感应线的形成，且每2个磁极通过气隙与吸附壁面形成类似于U形的磁铁，同时永磁吸附单元产生的磁力线与拢磁材料、钢制壁面形成有效的封闭磁回路，达到稳定吸附的目的。本文所设计的永磁吸附装置中的磁路排布方式采用N极对S极、S极对N极的交叉排列方式，永磁吸附单元上方为拢磁材料，用于增强对钢制壁面的吸附，使之形成封闭磁回路，以减少漏磁。轮腿式爬壁机器人通过3组车轮的依次提升来实现移动越障功能，其越障原理如图1（a）所示。在机器人移动过程中，应至少保证2组车轮与钢制壁面接触，最大越障高度为100 mm。永磁吸附装置安装在每组车轮中间的横梁上，如图1（b）所示。永磁吸附装置与钢制壁面之间的工作气隙可通过在装置与车轮横梁之间加减垫片或对轮胎充气来进行优化调整。与传统的磁轮吸附相比，所设计的非接触式永磁吸附装置可保证机器人在越障时不会因磁吸附力不足而产生倾覆后翻的现象，故其磁能利用率较高。

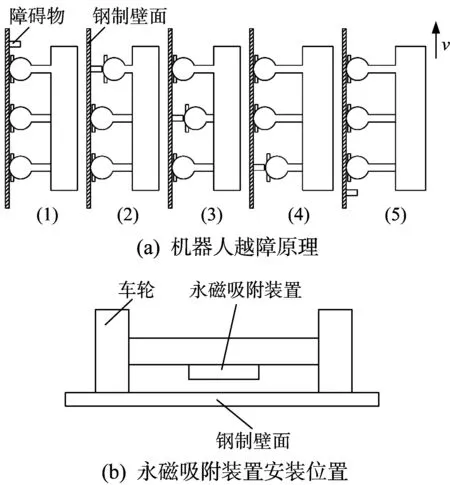
图1 轮腿式爬壁机器人的越障原理及永磁吸附装置的安装位置示意Fig.1 Obstacle-surmounting principle of wheel-legged wallclimbing robot and installation position of permanent magnet adsorption device

在永磁吸附装置长度不变的基础上，结合磁回路闭合原理，根据相邻永磁吸附单元之间以及两侧永磁吸附单元外侧是否有拢磁材料或隔磁材料，得到不同永磁吸附装置的二维磁路原理［15］，如图2所示，其中箭头方向为永磁吸附单元的充磁方向。现分别对相邻永磁吸附单元之间有拢磁材料或隔磁材料和无材料（两侧永磁吸附单元外侧有扰磁材料）以及所有永磁吸附单元两侧均无材料等4种永磁吸附装置设计方案进行对比分析。

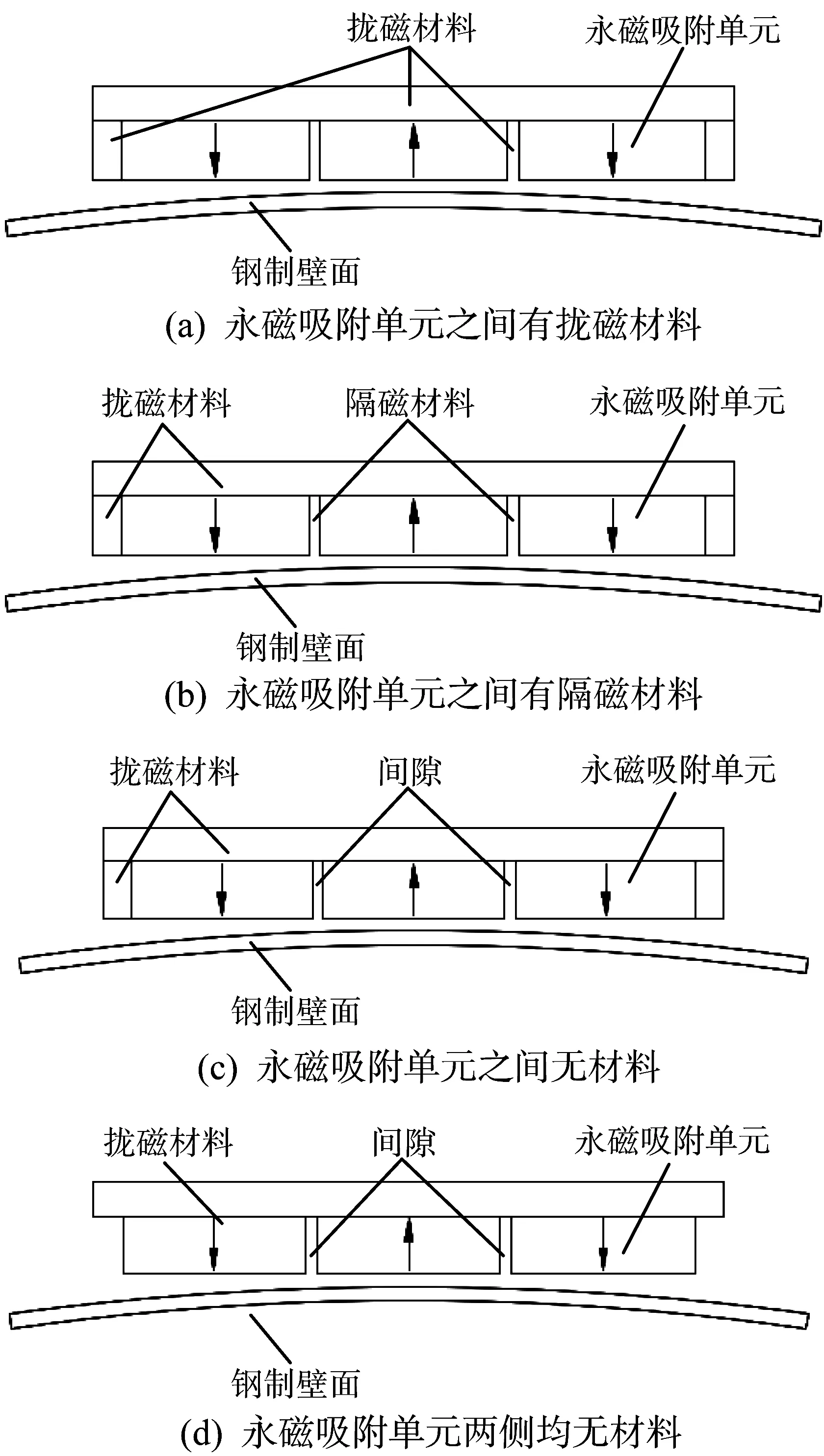
图2 4种永磁吸附装置的二维磁路设计原理Fig.2 Two-dimensional magnetic circuit design principle of four permanent magnet adsorption devices

4种永磁吸附装置设计方案均采用径向充磁，区别在于永磁吸附单元两侧是否有拢磁材料或隔磁材料，其中拢磁材料为导磁轭铁，隔磁材料为铝合金。为了验证上述4种设计方案的可行性，利用Ansoft Maxwell软件分别对4种永磁吸附装置进行磁力仿真分析，其中钢制壁面的半径为10 m，结果如图3所示。

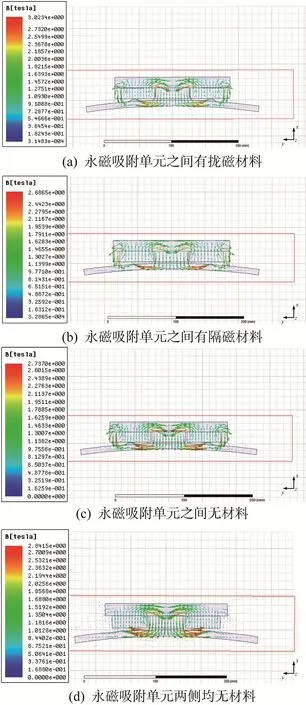
图3 4种永磁吸附装置的磁力线分布Fig.3 Distribution of magnetic field lines of four permanent magnet adsorption devices

通过Ansoft Maxwell软件仿真得到的4种永磁吸附装置的磁感应强度和磁吸附力如表1所示。由表1可知，图2（a）、图2（c）所示的永磁吸附装置外侧有拢磁材料，其与钢制壁面形成封闭的磁回路，相比于图2（d）所示的装置更能减少漏磁现象的发生；图2（c）所示永磁吸附装置的磁感应强度比图2（b）的略大，但其磁吸附力相同，而图2（d）所示永磁吸附装置的磁感应强度明显比图2（b）、图2（c）的大，但其对钢制壁面的磁吸附力较小。由于永磁吸附装置安装在轮腿式爬壁机器人前、中、后位置的底侧，须考虑机器人自身的重量以及遇到障碍时车轮依次抬升的情况，最终选择相邻永磁吸附单元之间无材料的设计方案，即图2（c）所示装置。

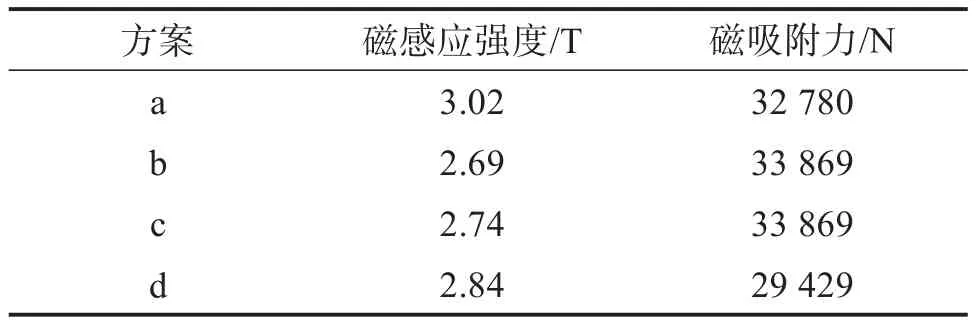
表1 4种永磁吸附装置的磁感应强度和磁吸附力对比Table 1 Comparison of magnetic induction intensity and magnetic absorption force of four permanent magnet adsorption devices

2 永磁吸附装置受力分析

根据静态磁场理论可知，导磁材料在静态磁场中受到磁力的作用。对于本文所设计的永磁吸附装置，其产生的磁吸附力可看作静态磁场对钢制壁面的磁力作用，则其永磁吸附单元的磁场能量Wm可表示为：

式中：V为磁场分布空间（B≠0 T）；B为磁极表面的磁感应强度；H为磁场强度。

进一步对磁场能量求导，可求得永磁吸附单元产生的磁吸附力F：

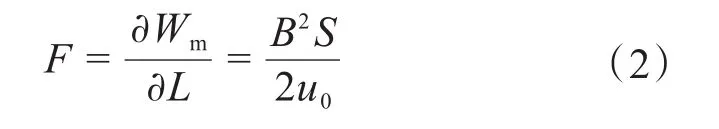
式中：S为永磁吸附单元与钢制壁面之间的工作气隙面积；u0为空气的磁导率。

从式（2）中可以看出，在实际计算永磁吸附单元产生的磁吸附力时未考虑工作气隙中的磁场，因此利用式（2）计算磁吸附力时存在一定的误差。当单个永磁吸附单元与钢制壁面存在一定气隙时，须计算钢制壁面的磁感应强度Bg。由于钢制壁面的曲率较小，如图4所示（图中：D、W和A分别为永磁吸附单元的长度、宽度和高度，X为永磁吸附单元表面中心点与钢制壁面的距离［16］，即工作气隙），此时钢制壁面的磁感应强度Bg为：

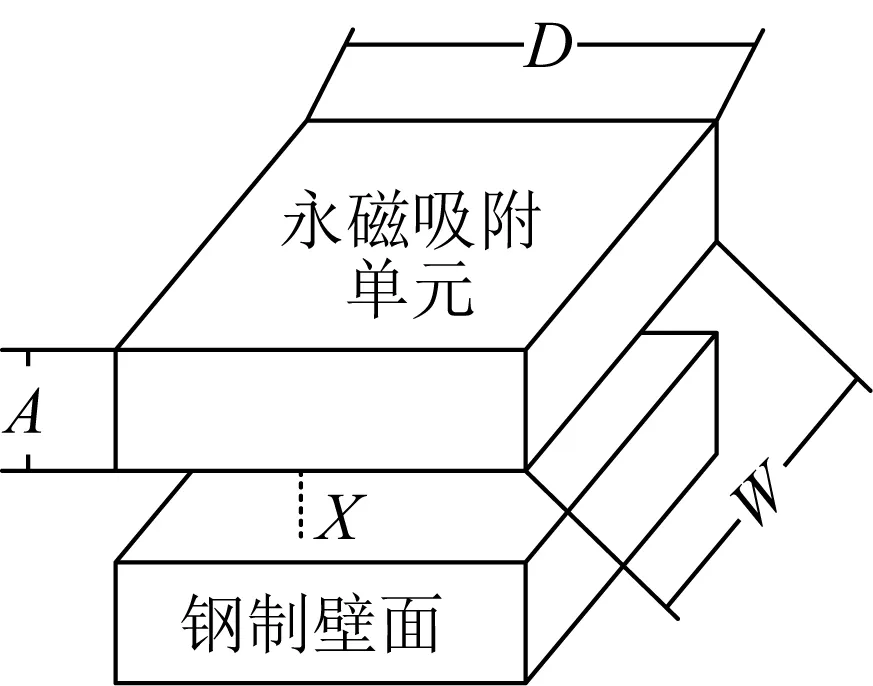
图4 永磁吸附单元对钢制壁面的吸附示意Fig.4 Schematic diagram of adsorption of permanent magnet adsorption unit to steel wall

式中：Br为钕铁硼永磁吸附单元的磁感应强度，Br=1.25 T。

故随着工作气隙的变化，永磁吸附单元产生的磁吸附力F为：

结合立面作业对爬壁机器人吸附功能的要求，对轮腿式爬壁机器人进行受力分析，如图5所示。

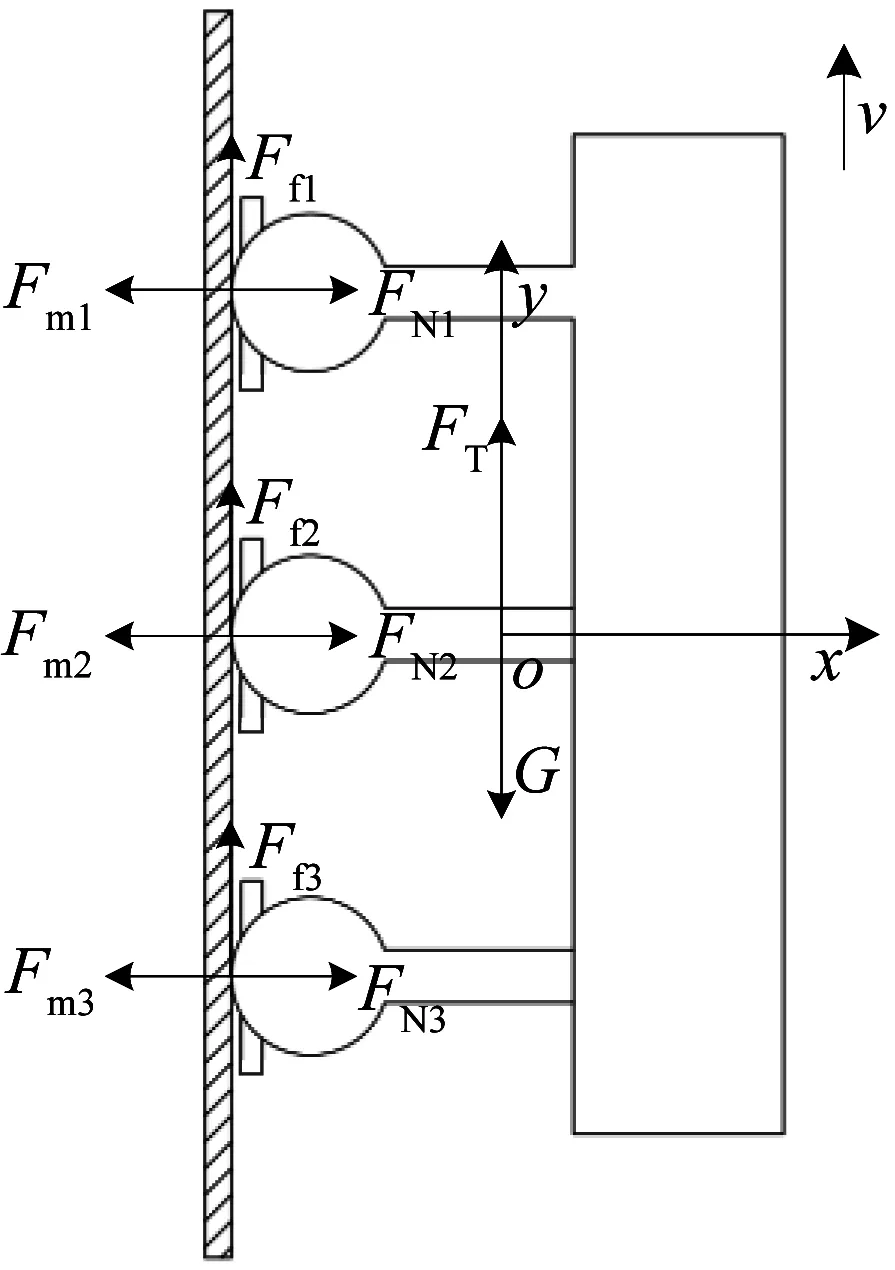
图5 轮腿式爬壁机器人受力分析Fig.5 Force analysis of wheel-legged wall-climbing robot

由图5可知，轮腿式爬壁机器人受重力G，钢制壁面对车轮的支持力FN1、FN2、FN3，摩擦力Ff1、Ff2、Ff3以及3个永磁吸附装置产生的磁吸附力Fm1、Fm2、Fm3的作用，则可得：

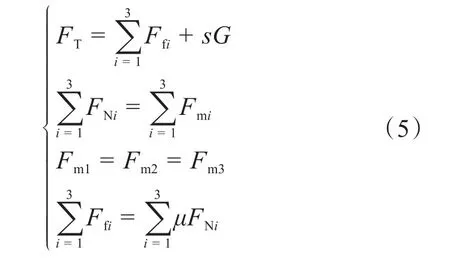
式中：FT为爬壁机器人的牵引力；s为车轮安全系数；μ为爬壁机器人车轮与钢制壁面之间的静摩擦系数。

由式（5）可得，各永磁吸附装置产生的磁吸附力为：

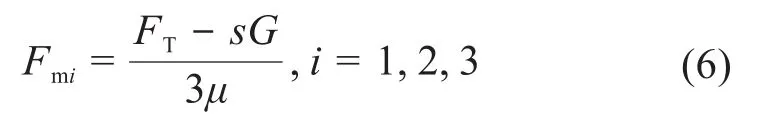
由式（4）和式（6）可知，永磁吸附装置对钢制壁面的磁吸附力的主要影响因素有永磁吸附单元的长度D、宽度W和高度A以及工作气隙X。此外，由于轮腿式爬壁机器人在钢制壁面上进行维护作业且其永磁吸附单元以磁极交叉的方式排布，故相邻永磁吸附单元气隙C，钢制壁面的厚度E、半径R以及拢磁材料厚度K对磁吸附力也存在一定的影响。对不同结构参数下永磁吸附装置的磁吸附力变化规律进行分析，可为轮腿式爬壁机器人的轻量化设计提供依据。

3 永磁吸附装置的仿真分析与结构参数优化

3.1 三维建模仿真

为了更符合实际应用的要求，以半径为10 m的石油化工储罐为建模基础，对永磁吸附装置进行结构参数优化设计。图6所示为永磁吸附装置的三维结构示意。图中：L为永磁吸附单元上方扰磁材料的截面长度，δ为外侧扰磁材料的截面宽度。

图6 永磁吸附装置结构示意Fig.6 Structure diagram of permanent magnet adsorption device

对永磁吸附装置进行仿真建模时，拢磁材料采用导磁轭铁，储罐钢制壁面材料采用Q235，永磁吸附单元材料采用钕铁硼（NdFeB-N35），其导磁率约为1.099 8；相邻永磁吸附单元间隙及其与钢制壁面之间的工作气隙内均为空气。所构建的永磁吸附装置吸附钢制壁面的三维仿真模型如图7所示。

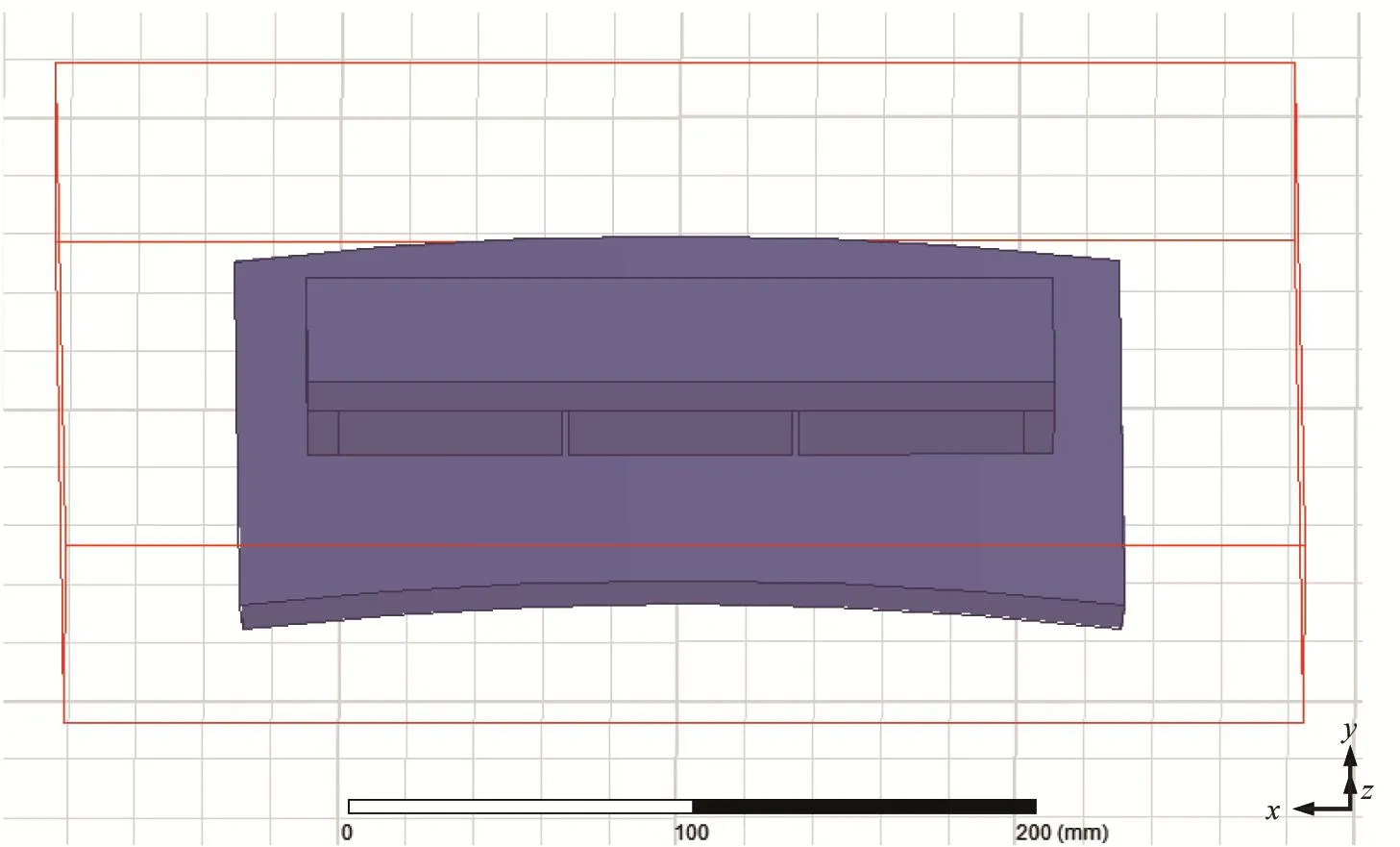
图7 永磁吸附装置吸附钢制壁面的三维仿真模型Fig.7 Three-dimensionalsimulation modelofpermanent magnet adsorption device adsorbing steel wall

3.2 结构参数优化

基于控制变量法的原理，设置永磁吸附单元上方扰磁材料的截面长度L=220 mm，外侧扰磁材料的截面宽度δ=10 mm，通过改变不同的结构参数，得到不同条件下永磁吸附装置对钢制壁面的磁吸附力的变化规律，从而获得适用于不同重量轮腿式爬壁机器人的永磁吸附装置的结构参数最优解。

3.2.1 工作气隙对磁吸附力的影响

在图7所示的三维仿真模型中，取D=66 mm，W=60 mm，A=16 mm，E=8 mm，C=2 mm，K=10 mm，R=10 m，对工作气隙X进行优化设计。取X=0～9 mm，通过仿真分析和直线拟合处理得到X对永磁吸附装置磁吸附力的影响，结果如图8所示。

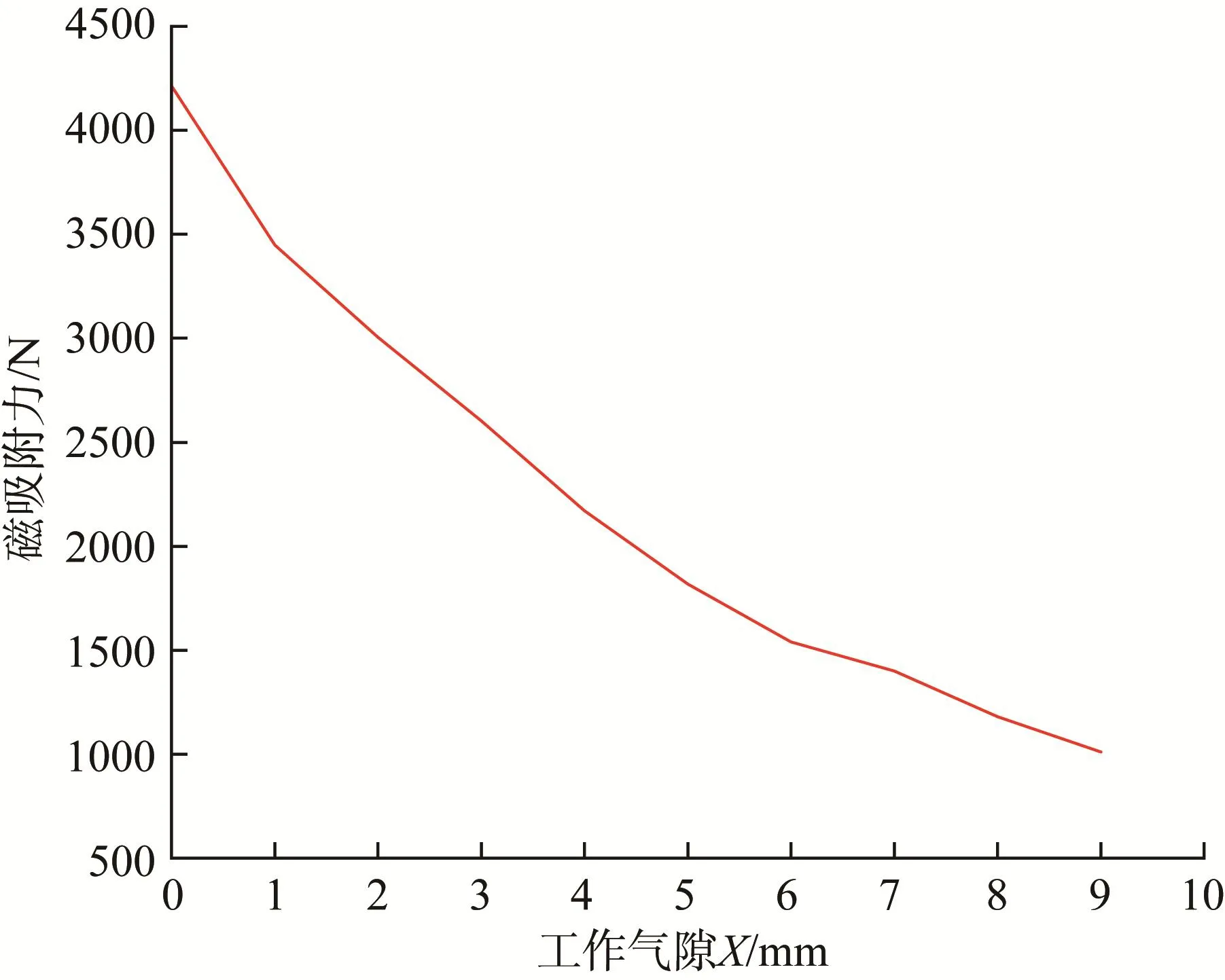
图8 工作气隙对永磁吸附装置磁吸附力的影响Fig.8 Influence of working air gap on magnetic adsorption force of permanent magnet adsorption device

由图8可知，随着工作气隙X的增大，永磁吸附装置的磁吸附力呈减小趋势；当永磁吸附装置与钢制壁面无气隙（即X=0 mm）时，其磁吸附力最大。结果表明，当相邻永磁吸附单元、扰磁材料与钢制壁面形成并联磁回路时，工作气隙越大，其形成的磁回路越大，则从气隙中漏磁的现象越严重，从而导致永磁吸附装置对钢制壁面的磁吸附力随之减小。因此，在实际应用中，在保证磁吸附力足以承受爬壁机器人重量的前提下，应尽量减小永磁吸附装置与钢制壁面的距离。

3.2.2 相邻永磁吸附单元间隙对磁吸附力的影响

同理，取 D=66 mm，W=60 mm，A=16 mm，E=8 mm，X=2 mm，K=10 mm，R=10 m，对相邻永磁吸附单元间隙C进行优化设计。取C=0～9 mm，通过仿真分析和直线拟合处理得到C对永磁吸附装置磁吸附力的影响，结果如图9所示。

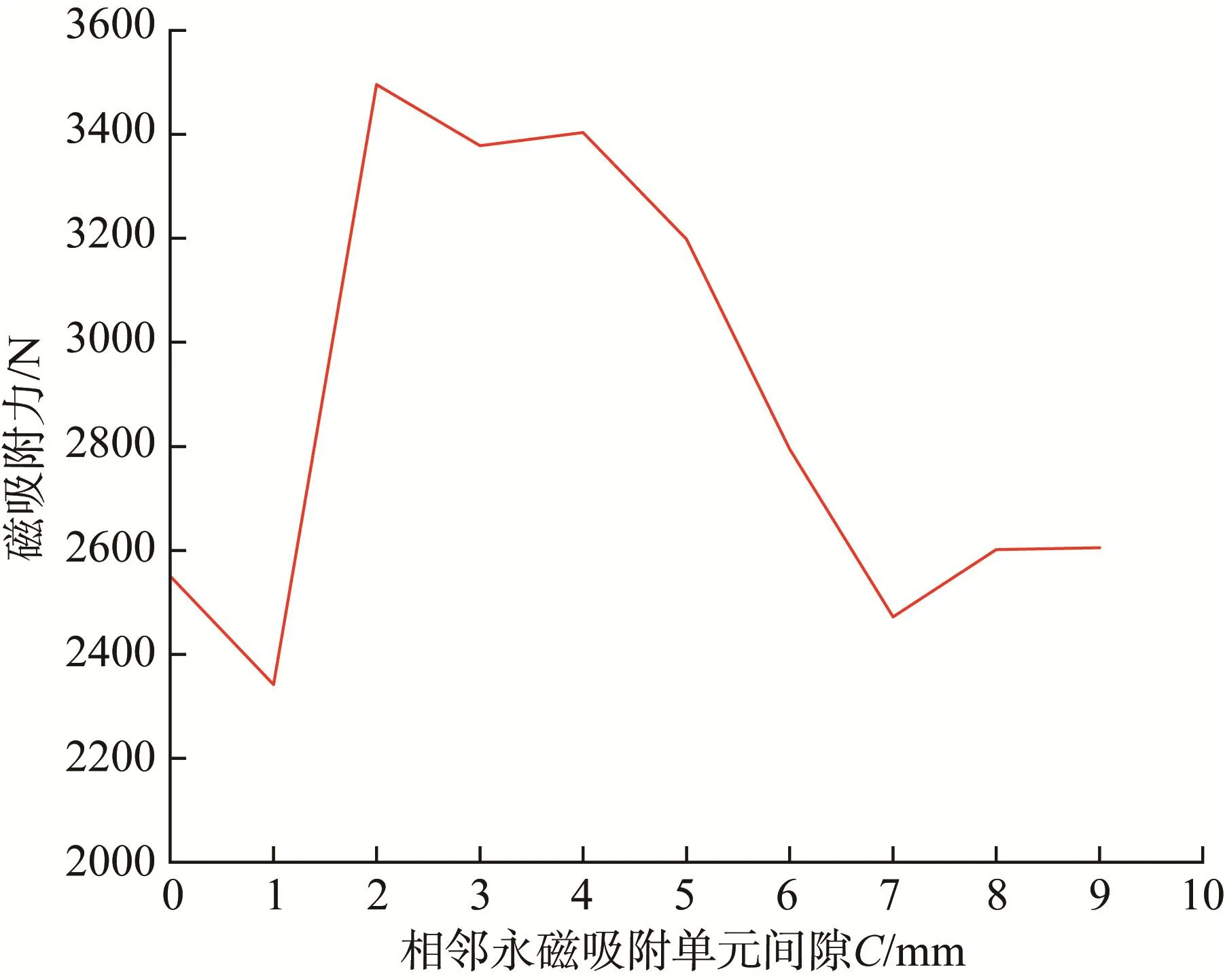
图9 相邻永磁吸附单元间隙对永磁吸附装置磁吸附力的影响Fig.9 Influence of gap between adjacent permanent magnet adsorption units on magnetic adsorption force of permanent magnet adsorption device

图9所示曲线出现了波峰，说明当相邻永磁吸附单元间隙C=2 mm时，永磁吸附装置的磁吸附力达到最大。这是因为当相邻永磁吸附单元不存在间隙时，永磁吸附单元、扰磁材料与钢制壁面形成的是单一的磁回路，而非并联磁回路，此时较少的磁力线穿过钢制壁面；而当间隙过大时，漏磁现象严重，导致永磁吸附装置对钢制壁面的磁吸附力大大减小。由此可得，当C=2～4 mm时，磁吸附力的利用率较高。

3.2.3 永磁吸附单元长度对磁吸附力的影响

同理，取W=60 mm，A=16 mm，E=8 mm，C=X=2 mm，K=10 mm，R=10 m，对永磁吸附单元长度D进行优化设计。取D=25～200 mm，通过仿真分析和直线拟合处理得到D对永磁吸附装置磁吸附力的影响，结果如图10所示。

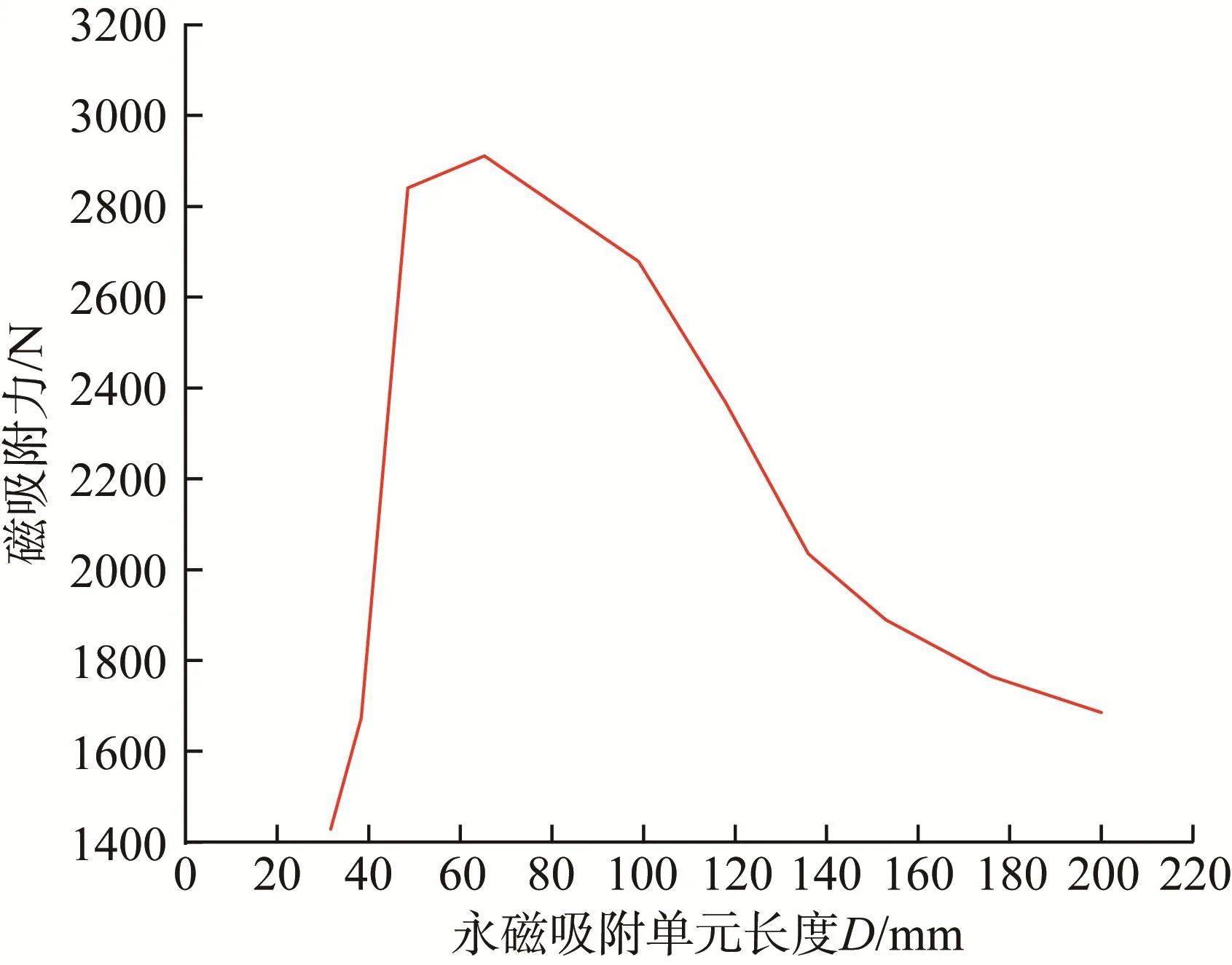
图10 永磁吸附单元长度对永磁吸附装置磁吸附力的影响Fig.10 Influence of permanent magnet adsorption unit length on magnetic adsorption force of permanent magnet adsorption device

图10所示曲线出现波峰，说明当永磁吸附单元长度D=60～70mm时，即永磁吸附单元的数量为3～5个时，永磁吸附装置的磁吸附力达到最大。在相邻永磁吸附单元间隙不变的情况下，当永磁吸附单元较长时，永磁吸附单元、扰磁材料与钢制壁面之间形成的闭合磁回路较大，对于一定厚度的钢制壁面和扰磁材料会产生一定的漏磁现象；当永磁吸附单元达到一定长度时，磁感应线不是遵循原来的途径返回，而是沿着比原先路径稍高的曲线返回，这会导致D＞65 mm后永磁吸附装置的磁吸附力呈下降趋势。在实际应用中，可适当增加永磁吸附单元的长度，以增大磁通量，从而抵消一部分经由相邻永磁吸附单元间隙泄漏的磁通。

3.2.4 永磁吸附单元宽度对磁吸附力的影响

同理，取D=66 mm，A=16 mm，E=8 mm，C=X=2 mm，K=10 mm，R=10 m，对永磁吸附单元宽度W进行优化设计。取W=40～90 mm，通过仿真分析和直线拟合处理得到W对永磁吸附装置磁吸附力的影响，结果如图11所示。

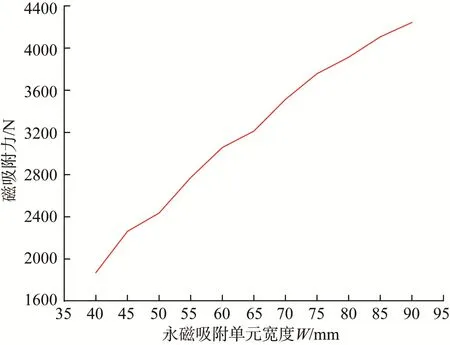
图11 永磁吸附单元宽度对永磁吸附装置磁吸附力的影响Fig.11 Influence of permanent magnet adsorption unit width on magnetic adsorption force of permanent magnet adsorption device

由图11可知，永磁吸附装置的磁吸附力在永磁吸附单元宽度W=40～90 mm时呈递增趋势。这是因为在永磁吸附单元宽度增加的同时，其与钢制壁面之间的工作气隙面积也随之增大，使得工作气隙中的磁通量无法达到饱和状态，从而导致磁吸附力一直呈增大状态。

3.2.5 永磁吸附单元高度对磁吸附力的影响

同理，取D=66 mm，W=60 mm，E=8 mm，C=X=2 mm，K=10 mm，R=10 m，对永磁吸附单元高度A进行优化设计。取A=8～16 mm，通过仿真分析和直线拟合处理得到A对永磁吸附装置磁吸附力的影响，结果如图12所示。

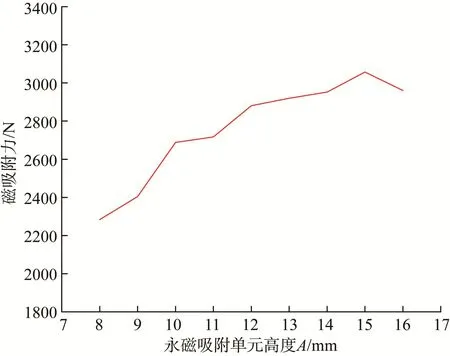
图12 永磁吸附单元高度对永磁吸附装置磁吸附力的影响Fig.12 Influence of permanent magnet adsorption unit height on magnetic adsorption force of permanent magnet adsorption device

由图12可知，永磁吸附装置的磁吸附力随永磁吸附单元高度A（8～15 mm）的增加呈递增趋势；当A=9～10 mm时，永磁吸附装置的磁吸附力增大较快，最后趋于饱和状态。在永磁吸附装置与钢制壁面之间的工作气隙不变的情况下，增加永磁吸附单元高度可使其磁通量增加，从而使工作气隙中的磁通量不断趋近于饱和状态，则磁吸附力最终达到稳定状态。

3.2.6 扰磁材料厚度对磁吸附力的影响

同理，取 D=66 mm，W=60 mm，A=16 mm，E=8 mm，C=X=2 mm，R=10 m，对扰磁材料厚度K进行优化设计。取K=4～10 mm，通过仿真分析和直线拟合处理得到K对永磁吸附装置磁吸附力的影响，结果如图13所示。

由图13可知，永磁吸附装置的磁吸附力随扰磁材料厚度K的增加而增大，最后趋于饱和状态。这是因为当扰磁材料较薄（即K较小）时，永磁吸附单元所产生的磁通密度大于扰磁材料的饱和磁通密度，则永磁吸附装置的漏磁量增大，使得通过钢制壁面的磁通量减少，从而导致磁吸附力减小；当扰磁材料达到一定厚度时，通过扰磁材料的磁回路保持稳定，其厚度的增大对磁吸附力的影响不再明显。

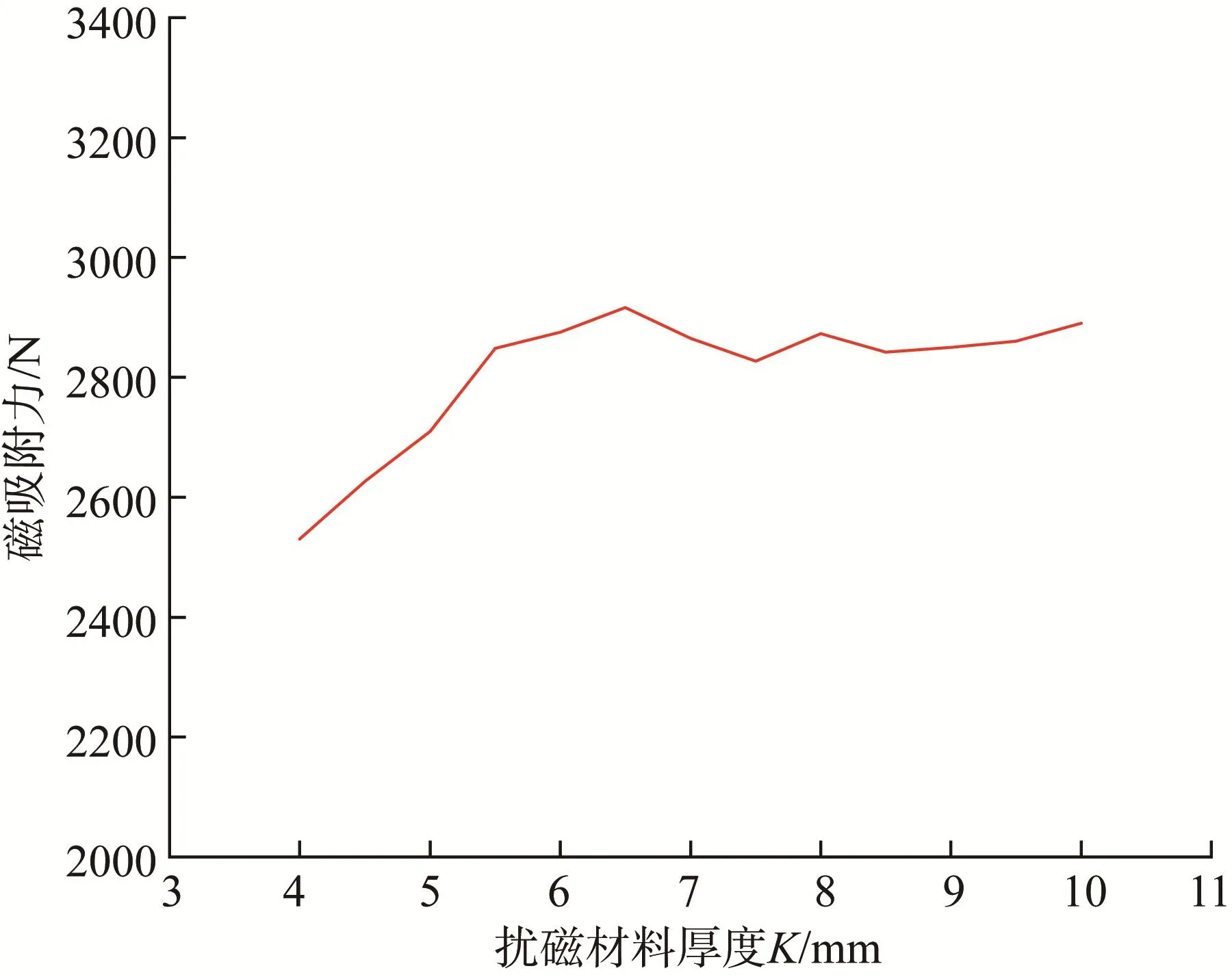
图13 扰磁材料厚度对永磁吸附装置磁吸附力的影响Fig.13 Influence of magnetic disturbing material thickness on magnetic adsorption force of permanent magnet adsorption device

3.2.7 钢制壁面厚度对磁吸附力的影响

同理，取D=66 mm，W=60 mm，A=16 mm，C=X=2 mm，K=10 mm，R=10 m，对钢制壁面厚度E进行优化设计。取E=4～15 mm，通过仿真分析和直线拟合处理得到E对永磁吸附装置磁吸附力的影响，结果如图14所示。

图14 钢制壁面厚度对永磁吸附装置磁吸附力的影响Fig.14 Influence of steel wall thickness on magnetic adsorption force of permanent magnet adsorption device

由图14可知，永磁吸附装置的磁吸附力随钢制壁面厚度E的增加而增大，最后趋于饱和状态。当钢制壁面较薄（即E较小）时，永磁吸附单元所产生的磁回路穿透钢制壁面，永磁吸附装置的漏磁量增大，导致磁吸附力减小；当钢制壁面达到一定厚度时，穿过钢制壁面的磁力线达到饱和，则其厚度变化对磁吸附力的影响不再明显。

3.2.8 钢制壁面半径对磁吸附力的影响

考虑到实际应用中储罐钢制壁面的半径不同，结合上文得到的各结构参数的最优解，即D=66 mm，W=60 mm，A=15 mm，E=8 mm，C=X=2 mm，K=6 mm，对钢制壁面半径R进行优化设计。取R=5～10 m，通过仿真分析和直线拟合处理得到R对永磁吸附装置磁吸附力的影响，结果如图15所示。

图15 钢制壁面半径对永磁吸附装置磁吸附力的影响Fig.15 Influence of steel wall radius on magnetic adsorption force of permanent magnet adsorption device

由图15可知，永磁吸附装置的磁吸附力随钢制壁面半径的增大而增大。这是因为当钢制壁面半径增大时，其相应的曲率随之减小，而扇形壁面更接近平面，即永磁吸附装置与钢制壁面之间的距离分布得更加均匀，则在工作气隙处的漏磁现象减少，从而使得对钢制壁面的磁吸附力增大。图16所示为R=10 m时永磁吸附装置的磁场强度分布云图。由图16可知，当相邻永磁吸附单元形成完整的磁回路并呈并联式分布时，其间隙处的磁场强度较大，且永磁吸附单元下侧的磁场强度最大。

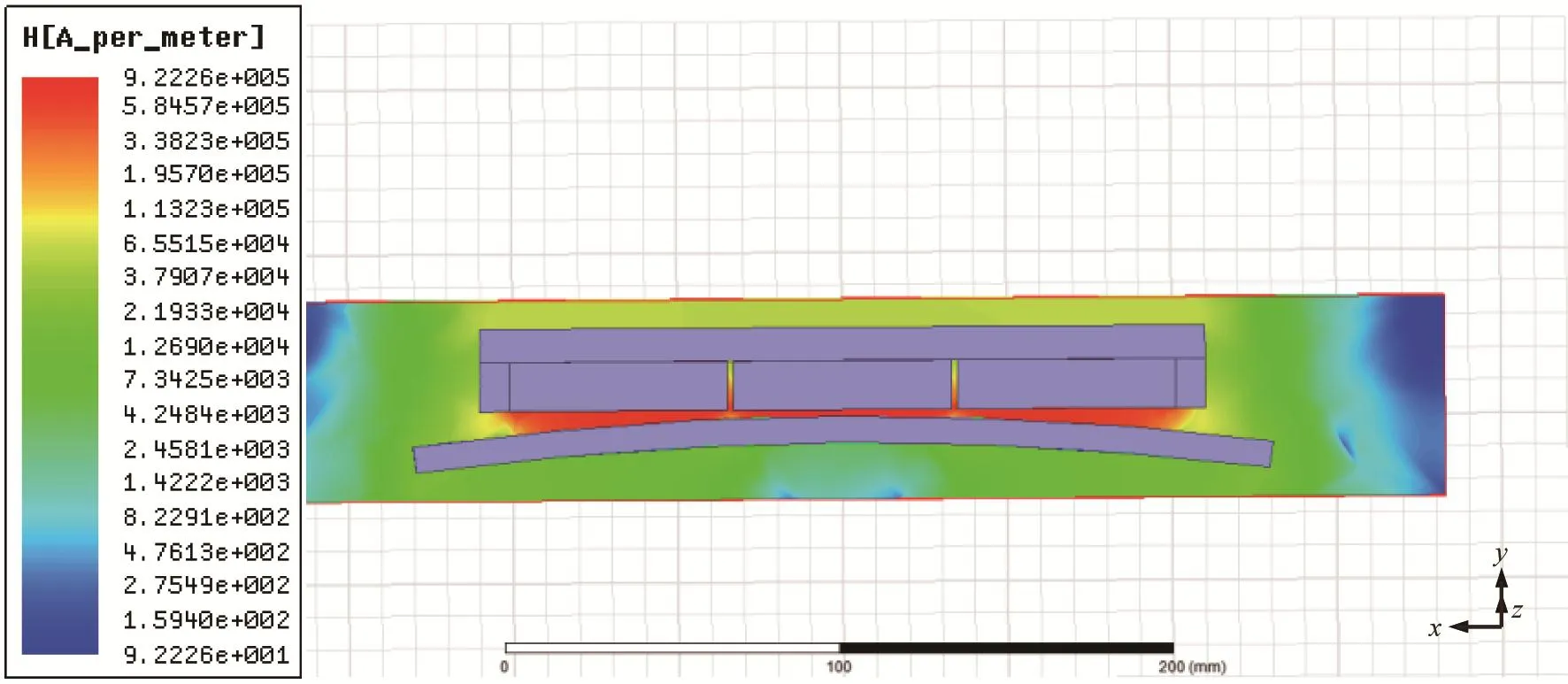
图16 永磁吸附装置的磁场强度分布云图（R=10 m）Fig.16 Cloud map of magnetic field strength distribution of permanent magnet adsorption device（R=10 m）

4 实验验证

为了验证上述优化结果的准确性，本文制作了如图17所示的简易永磁吸附装置，通过实验对优化结果进行验证。为了便于测试，钢制壁面采用无曲率钢板，永磁吸附装置的主要结构参数均采用实际加工尺寸，即：永磁吸附单元上方扰磁材料的截面长度L=110 mm，外侧扰磁材料的截面宽度δ=9 mm，永磁吸附单元长度D=29 mm，永磁吸附单元宽度W=64 mm，永磁吸附单元高度A=12 mm，相邻永磁吸附单元间隙宽度C=2 mm，扰磁材料厚度K=12 mm。

图17 简易永磁吸附装置实物Fig.17 Simple permanent magnet adsorption device

由于永磁吸附装置加工周期长，若做多组实验的话，则须加工多个永磁吸附装置；此外由于装置的磁吸附力较大，实验的危险性较大，出于安全考虑，只对其中一组变量进行实验验证。在永磁吸附装置整体尺寸不变的情况下，以工作间隙X为单一变量，通过实验得到其磁吸附力随X（1～10 mm）的变化情况，并与仿真结果进行比较，如图18所示。从图18中可以看出，优化后永磁吸附装置的磁吸附力的实测值比仿真值平均约高16.45%，但实测值与仿真值存在一定误差，这主要是因为：1）钢板表面存在一些凹凸不平的弧坑、焊点，同时因长期遭受风雨而腐蚀，其表面较为粗糙；2）受实验条件的影响，实验用永磁吸附装置与钢板之间夹有一定厚度的薄板（2～10 mm不等），薄板与空气的导磁率存在一定的偏差；3）所制作的永磁吸附装置的实际尺寸与理论尺寸存在一定偏差；4）实验采用法兰盘逐个加载，加载时存在一定误差，同时承载笼在加载时也存在一定程度的震荡。

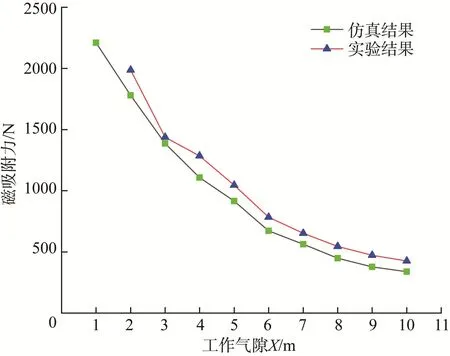
图18 永磁吸附装置磁吸附力实验结果与仿真结果对比Fig.18 Comparison of experimental results and simulated results of magnetic adsorption force of permanent magnet adsorption device

5 结 论

采用非接触式永磁吸附的爬壁机器人具有较好的立面越障功能，为了确保其运动的可靠性，本文针对轮腿式爬壁机器人永磁吸附装置进行了设计与优化。基于控制变量法和有限元仿真对永磁吸附装置进行参数化分析，确定在钢制壁面半径为5～7 m时，相邻永磁吸附单元间隙及永磁吸附单元数量对磁吸附力的影响较大，当相邻永磁吸附单元间隙为2～4 mm及永磁吸附单元数量为3～5个时，磁吸附力的利用率较高。最后，通过制作优化后的简易永磁吸附装置，利用实验得到了其磁吸附力随工作间隙的变化曲线，实际测得的磁吸附力虽比仿真值大，但误差较小，这在一定程度上验证了结构参数优化仿真结果的准确性。通过对永磁吸附装置的有限元分析与实验验证结果可知，优化后永磁吸附装置产生的磁吸附力的实测值比仿真值平均约高16.45%，其能有效保证轮腿式爬壁机器人在立面上稳定运动。所设计的永磁吸附单装置及其结构优化结果可为采用永磁吸附的爬壁机器人的设计提供理论支撑，从而获得可靠的磁吸附方案。