集成改进AHP与XGBoost算法的食品安全风险预测模型：以大米为例

王小艺， 王姿懿， 赵峙尧,*， 张 新， 陈 谦， 李 飞

(1.北京工商大学 人工智能学院， 北京 100048；2.北京工商大学 国家环境保护食品链污染防治重点实验室， 北京 100048；3.北京服装学院， 北京 100029)

随着我国经济社会的快速发展，人民生活水平不断提高，老百姓对食品安全的关注程度日渐提高[1]。在食品安全风险管理中，食品安全风险评估是以数据为基础，在食源处分析与解决食品安全问题强有力的手段。2009年我国颁布实施的《中华人民共和国食品安全法》规定：“国家建立食品安全风险监测制度，由国务院卫生行政部门会同国务院食品安全监督管理等部门，制定、实施国家食品安全风险监测计划，成立由医学、农业、食品、营养、生物、环境等方面的专家组成的食品安全风险评估专家委员会进行食品安全风险评估。”[2]该规定突出强调了开展食品安全风险评估与预测具有极强的现实意义。

当前，风险评价方法主要包括主观赋权评价法、客观赋权评价法，以及综合主客观赋权评价法三大类。主观赋权评价法中层次分析法(analytic hierarchy process，AHP)和德尔菲(Delphi)法是目前比较成熟的风险评估方法。AHP通过构建目标层、准则层、方案层的三层结构来处理复杂的多目标决策问题[3]，但仍存在结构复杂，易受权威人士影响等不足[4]；Delphi法是一种依赖于众多专家意见的反馈匿名函询法[5]，通过不断整合、归纳、统计，匿名反馈最终得到一致的意见，但收集汇总专家意见的过程相对复杂，花费时间较长[6]。客观赋权评价法中多层前馈(back propagation，BP)、随机森林(random forest，RF)、支持向量机(support vector machine，SVM)等算法应用较为广泛。BP算法[7]是一种速度较快的梯度下降算法，具有较强的非线性映射能力，但容易陷入局部最小值等问题；RF算法[8]是Bagging的一个扩展变体，计算复杂度不高，但容易出现过拟合问题；SVM算法[9]具有较强的泛化能力，但不适用于大数据集。综合主客观赋权评价法是通过主观赋权评价法构建指标体系，依据客观赋权评价法构建风险预测模型，进而实现精准高效的风险评估。

现有的风险评价方法在实际应用中仍具有一定的局限性[10]，存在主观分析人工成本较高且评估进程较长，客观分析评估指标精度较低或过拟合性能较弱等问题，使得风险预测结果的准确率偏低且时间成本较高，从而造成缺失精准定位风险值的能力。因此，针对食品行业特性，本研究引入危害物最大残留限量(MRL)与危害物每日容许摄入量(ADI)对AHP进行定量改进，并与预测准确性高且不易过拟合的极端梯度提升树(extreme gradient boosting，XGBoost)算法相结合构建预测模型，应用于食品安全风险评估。通过除港澳台外全国31个省的大米检测数据为基础进行案例分析，利用改进后的AHP模型提取多维复杂数据中的综合特征值作为预测模型风险值，并将精度高、稳定性强的XGBoost算法作为训练模型应用于风险值预测，同时将相同数据应用于经典预测算法中进行对比，以验证XGBoost算法的有效性。

1 数据来源与数据清洗

1.1 数据来源

以2018年大米危害物检测数据为基础进行实例分析。通过搜集与整合国家食品安全抽检检验信息系统中的数据，得到除港澳台以外全国31个省市的大米危害物检测数据。此数据主要由抽检省份、抽检时间、抽检项目、检验结果等类别组成，其中危害物检测项目包含总汞、无机砷、铅、铬、镉、黄曲霉毒素B等危害物，部分数据如表1。

表1 2018年大米危害物检测原始数据Tab.1 Raw data of rice hazard detection in 2018

1.2 数据清洗

针对1.1节采集的危害物检测数据，为了从高维复杂的数据中提取有效信息，实现数据价值隐性到显性的蜕变[11]，本研究依次采用数据筛选、数据规约以及数据变换的手段对原始数据进行数据清洗，具体流程如图1。

图1 数据清洗流程Fig.1 Data cleaning process

1.2.1风险因子筛选

风险因子是指大米在生产、加工、包装、贮存、运输、销售直至食用等过程中产生的或由环境污染带入的、非有意加入的化学性危害物质[12-13]，其筛选流程如下。1)按照检测结果属性的不同进行分类。将每种危害物的检测结果分为描述型结果、数值型结果、以及空值三类，其中描述型结果主要包括未检出或小于某一具体数值(如<0.01 μg/kg)，数值型结果为具体检出量(如0.11 μg/kg)。2)描述型结果转换为数值型结果。由于数值型结果相比于描述型结果更能直观反映危害物含量的多少，针对小于某一具体数值的描述型结果删除多余符号。例如：黄曲霉毒素B检测含量为“<0.001 μg/kg”，而国家标准黄曲霉毒素B限定值为10 μg/kg，检测结果未超过国家标准限定值，则删除“<”符号，并将检测含量值记录为“0.001 μg/kg”；赭曲霉毒素A未检出，则将检测含量值记录为“0 μg/kg”。3)统计各危害物数值型结果的个数以及各危害物超过国家限定指标值的个数。按照危害物超过国家限定指标值的个数与危害物数值型结果的个数的比值从大到小依次排列，选取比值较大的危害物作为风险因子。依据筛选流程构建大米危害物风险指标体系，如表2。

表2 大米危害物风险指标体系Tab.2 Risk index system of rice hazard

1.2.2数据规约

数据规约主要包含数据集成和数据类型统一两个步骤。其中数据集成是指具有不同属性或不同格式的数据按照逻辑集成；而数据类型统一是指数值型数据全部统一为浮点数型，便于数据的统一管理。

1.2.3数据变换

数据变换同样分为噪声过滤与数据归一化两个步骤。其中噪声过滤是指剔除数据中无法解释的数据变动，即删除数据缺失值以及去除数据异常值。由于原始数据的检验结果与结果单位处于分离并行的状态，因此本研究的异常值为单位记录错误导致的统计误差，即在检测数据中数值超过全部原始数据均值500倍以上的数据。

同时为保证风险因子的输入质量，将数据进行归一化处理，即将数据按照合适的隶属度曲线标准化映射到特定的数据空间，本研究采用的是梯形隶属度函数，见式(1)。

(1)

式(1)中，xmin为无风险的最大值，其中无风险是指该风险因子检测值大幅低于国家限定指标值，则选取危害物国家限定指标值的百分之一作为无风险最大值；xmax为国家限定指标值。将处理后的数据代入隶属度函数，计算得到综合特征值并标记为预测模型风险值。

2 集成改进AHP与XGBoost算法的风险预测模型建立

2.1 风险预测模型框架

通过对多维复杂的大米危害物检测数据进行数据清洗操作，得到了大米危害物的各风险因子指标，以这些风险因子指标值为基础，构建了一种集成改进AHP与XGBoost算法的危害物风险预测模型。其中，由于AHP受主观因素影响较大的，因此针对食品安全领域特性，结合ADI和MRL对其进行定量改进，同时应用拟合程度高、速度快的XGBoost算法进行特征学习，提取危害物的综合特征值，具体流程如图2。

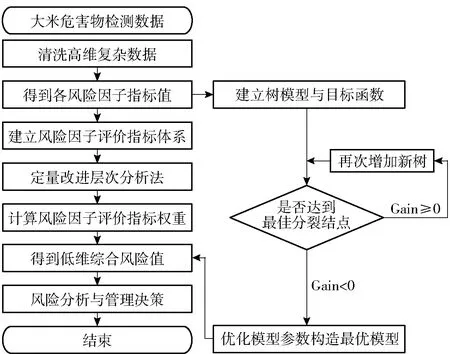
图2 风险预测模型框架Fig.2 Framework of risk forecast model

2.2 层次分析法定量改进

AHP是一种综合定量与定性分析的系统分析方法，能够科学系统地进行多目标的决策分析[14]。其基本思路是按照指标体系的层次结构，采用由专家打分的1～9标度法计算指标权重，从而将复杂高维数据转换成若干低维综合因素[15]。但由于专家打分受主观因素影响较大且需要较高的人工成本[16]，为了解决这一问题，考虑到按照优良农业措施生产的食品在消费时实际的残留范围，以及允许的残留水平，通过引入世界卫生组织设定的食品上的残留浓度最大残留限量，采用由各危害物ADI与MRL结合形成的相对权重指标代替专家打分建立判断矩阵，以得到各指标权重值，使各指标权重值相较于传统AHP更具客观性。

首先，设存在k个风险因子，则评价风险因子的指标权重可表示为矩阵Nk×2[式(2)]：

(2)

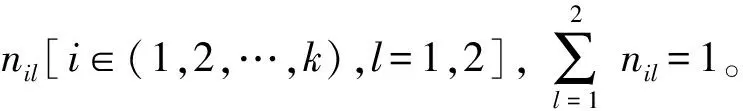
设评价风险因子的指标值为矩阵M2×k[式(3)]：

(3)

式(3)中，m1i[i∈(1,2,…,k)]表示第i个风险因子的ADI；m2i[i∈(1,2,…,k)]表示第i个风险因子的MRL。

将评价风险因子的指标权重矩阵与评价风险因子指标值矩阵相结合，组成判断矩阵Ak×k[式(4)]，同时，融合专家干预建议对判断矩阵Ak×k进行准确性验证和结果校正。

(4)

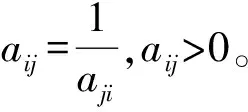
表3 判断矩阵中的元素标度Tab.3 Element scale of judgment matrix

根据判断矩阵计算最大特征根λmax以及特征向量W=[w1,w2,…,wk]T[式(5)～式(7)]：

AW=λmaxW;

(5)

(6)

(7)

经归一化后的特征向量W记为风险因子权重值，其可以反映各风险因子危害程度的大小[17]，利用1.2节方法对冗余数据清洗分类，形成包含q条数据、k个维度的风险因子矩阵X[式(8)]：

(8)

将矩阵X与各风险因子指标权重加权，得到低维综合风险值Y[式(9)]：

(9)

因此，采用改进的AHP模型对食品检测数据进行降维，得到低维综合风险值，再利用食品安全风险评估领域特有的定量指标，即MRL与ADI，作为评判标准，以提高风险值的准确性及客观性，进而得到大米危害物风险预测模型的期望输出。

2.3 极端梯度提升树算法训练

XGBoost算法[10]是一种支持并行计算的梯度提升树算法，是在梯度提升迭代决策树(gradient boosting decision tree，GBDT)的基础上对代价函数进行二阶泰勒展开得到的。XGBoost算法在提升了运行速度以及预测准确率的同时，也有效抑制了过拟合现象[18]。XGBoost算法训练流程如图3。

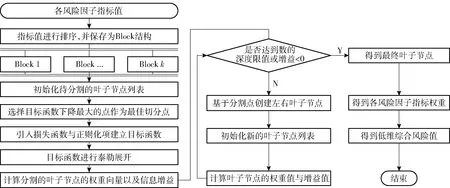
图3 XGBoost 算法训练流程Fig.3 Training process of XGBoost algorithm

其数学模型可表示为式(10)、式(11)：

(10)

F=f(xi)=wq(x)。

(11)

式(10)和式(11)中，i∈(1,2,…,n)为样本数量，i为低维综合风险值，xi为各风险因子指标值，t为子模型总数，wq(x)为XGBoost上全体叶子节点的权重向量，fk为在第k棵回归树上每个叶子结点的权重，F为对应所有回归树的集合。

定义损失函数l(yi,i)=(yi-i)2，即低维综合风险值与低维综合风险值预测值之间的误差维度；损失函数l(yi,i)的最优解F*(x)=arg minE(x,y)[L(y,F(x))]，用于辅助选取合适的叶子节点数，可防止叶子节点个数的无限增长，有效的节约模型运行时间；正则化项Ω(ft)[式(12)]，可防止XGBoost算法中叶子结点个数无限增长，加快模型运行速度。

(12)

式(12)中，γ和λ是调整参数，用于防止模型出现过拟合现象；T为叶子节点个数。正则化项与节点数呈正相关，因此引入正则化项可在保证低维综合风险预测值与风险值的误差稳定时快速得出叶子节点饱和值，从而提高模型的运行速度[19]。

引入由损失函数与正则化项组成的目标函数Obj(t)[式(13)]：

(13)

为了使目标函数梯度下降的更快更准，对目标函数Obj(t)进行泰勒展开得到如下目标函数Obj(t)[式(14)～式(17)]：

(14)

gi=∂l(yi,(t-1))；

(15)

(16)

(17)

鉴于此，问题的主要矛盾转化为求解以下2个二次函数[式(18)、式(19)]的最小值问题。

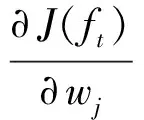
(18)

(19)

为避免多次枚举造成运算量过大，采用贪心算法寻求最优树结构，对已知叶子节点加入新的分割[20]，依次获得分割后的增益，计算见式(20)。

(20)

式(20)中，Gain表示信息增益是树形结构是否分支的主要参考因素，即当新分割产生的信息增量达到树的深度限值或Gain<0，树停止分割，从而在防止过拟合的前提下达到速度快拟合佳的仿真效果。

3 结果与分析

3.1 不同模型的优化参数配置

本研究的实验环境是i5- 6200U CPU、8G RAM的Win10操作系统，代码基于Jupyter Notebook平台通过Python3实现。基于此环境配置，将1.2节选取的各风险因子指标值作为风险预测模型输入数据，低维综合风险值作为风险预测模型输出数据，按照3∶1的训练测试比对数据集进行划分，并将XGBoost算法的模型预测结果与经研究证实预测效果较突出的主流模型预测结果进行对比分析，即最邻近分类(k-nearest neighbor，KNN)算法、SVM算法、BP算法、长短期记忆人工神经网络(long short-term memory，LSTM)算法。由于各算法配置的参数各异，故针对每个算法分别选取几个参数采用scikit-learn提供的随机搜索(RandomizedSearchCV)来进行参数配置。各模型参数配置结果如表4。

表4 不同算法的模型参数配置Tab.4 Model parameters configuration of different algorithms

在表4中，KNN算法的最佳参数配置由近邻数(neighbors)、预测权函数(weights)以及指定计算最近邻的算法(algorithm)组成。SVM算法的最佳参数配置由惩罚系数(C)、核函数(kernel、gamma、degree)以及距离误差(epsilon)组成；其中gamma与degree为SVM算法选择多项式核函数(poly)作为核函数后，该函数自带的参数，隐含地决定了数据映射到新的特征空间后的分布。BP算法的最佳参数配置由迭代次数(nb_epoch)、训练1次所选取的样本数(batch_size)、优化器(optimizer)以及激励函数(activation)组成。LSTM算法的最佳参数配置与BP算法相似，最佳参数配置同样由迭代次数(epochs)、训练1次所选取的样本数(batch_size)、优化器(optimizer)以及激励函数(activation)组成。XGBoost算法的最佳参数配置由迭代次数(n_estimators)、样本的采样率(subsample)、随机数种子(random_state)、学习率(learning_rate)以及每棵二叉树的最大深度(max_depth)组成。

3.2 模型精度分析

基于3.1中的仿真配置，利用不同风险预测模型，在各算法的训练次数均为200次的条件下，可得出各类风险因子风险值与不同模型预测值的对比，见图4。其中X轴代表样本编号；Y轴表示各类危害物的污染程度，即低维综合风险值。低维综合风险值大于1(y>1)即污染程度大于1，代表该危害物明显超标；且当y∈(0,1)时，矩阵Y中数值的大小与该类危害物污染程度呈正相关。

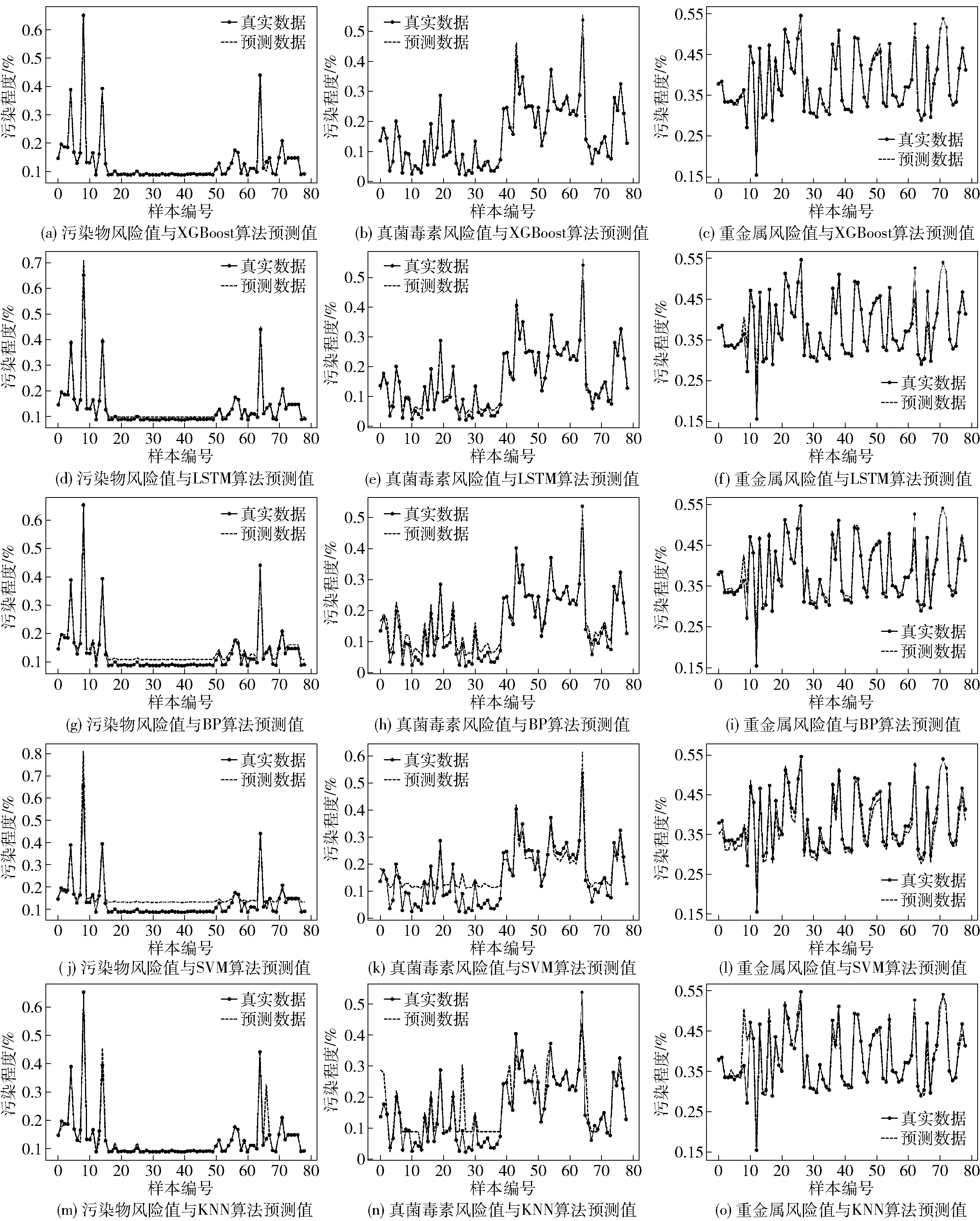
图4 各类风险因子风险值与不同模型预测值对比Fig.4 Comparison between risk values of various risk factors and predicted values of different models

由图4的15个模型对比曲线可知，当y∈(0.2,0.8)时，即各类危害物的污染程度处于合理区间时，各种模型的预测值与真实值的重合度较高；而当y∈(0,0.2)∪(0.8,+∞)时，即各类危害物的污染程度偏低或偏高时，部分模型(KNN、SVM、BP)平均拟合效果较差，在污染程度较高(较低)时易出现污染程度被高估(低估)的情况。

为更清晰地对比各模型实验结果，本研究采用相关系数R2、平均绝对误差MAE、平均平方误差MSE这3个指标对模型进行评估，各指标计算见式(21)～式(23)。

(21)

(22)

(23)

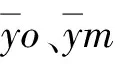
由表5可知，XGBoost算法的相关系数R2区间跨度小于一个百分点，在各类危害物预测实验中表现尤为稳定，且相比于其他模型，XGBoost算法的R2普遍偏高，均高达99%以上。同样，XGBoost算法的MAE和MSE，无论是区间跨度还是取值大小均低于其他模型，说明该模型在各类危害物预测实验中均具有良好的学习能力。综合对比5种算法，XGBoost算法相比于其他算法在预测方面具有更高的准确性以及更强的稳定性，因此可以更加直观准确地预测及分析食品安全危害物风险值。

4 结 论

本研究针对高维复杂且非线性的食品安全检测数据带来的数据利用率低及人工成本高等问题，综合考虑食品行业特有的相关危害物限定标准，对降维模型AHP进行定量改进，并与运行精度高的XGBoost算法相结合，提出了一种集成改进AHP与XGBoost算法的食品安全风险预测模型。基于此，本研究在全国除港澳台以外各省大米危害物检测数据的基础上，首先采用数据规约、数据变换及数据归一化方法将原始数据处理为结构化数据，随后采用定量改进的AHP模型提取低维综合风险值，最后采用XGBoost算法自适应地挖掘风险因子与低维风险值之间的关系。通过对比模型的仿真结果，集成改进AHP与XGBoost算法的风险预测模型在准确性和稳定性方面优于其他传统风险预测模型。因此，集成改进AHP与XGBoost算法模型的建立可以快速准确地识别出各类危害物的风险值，从而希望为监管部门评估决策提供科学有效的依据；但该模型在一些方面还值得改进，如在数据应用方面，由于各类食品危害物检测项目的不同，若采用动态权重赋权法进行权重配比将更符合实际需求；在模型应用方面，若应用于全供应链各环节实时监测风险值变化将有助于减少食源处风险威胁。

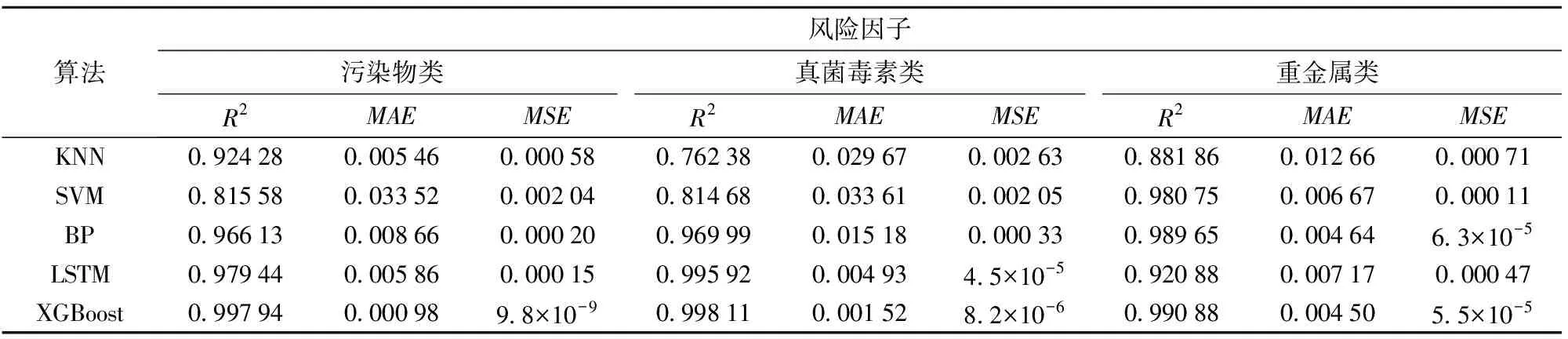
表5 不同算法的模型评估指标对比Tab.5 Comparison of model evaluation indexes of different algorithms