非线性快速批次过程高效迭代学习预测函数控制

马乐乐 刘向杰

随着现代工业中产品种类的增多和市场需求变化的加快,批次生产过程占据越来越重要的地位[1].这类生产过程通常需要按照一定顺序对原料进行加工,并进行重复操作来获得成批同类产品[2].批次过程具有 “多重时变”的特点[1],其控制任务通常为重复地以高精度跟踪参考轨迹.经典控制理论多基于连续生产过程中的调节问题,难以在批次过程中取得理想的控制效果.因此,发展适应批次过程特点的特殊控制算法具有重要理论意义和应用价值.

迭代学习控制(Iterative learning control,ILC)作为一种智能控制方法,可以通过迭代功能不断调整控制输入以提高跟踪性能,这与批次过程的结构十分契合,因此被广泛应用于批次过程控制[3-4].然而,ILC 是典型的开环控制,难以保证时域鲁棒性和闭环稳定性,限制了其在实际工业中的应用.模型预测控制(Model predictive control,MPC)作为一项成熟的先进控制技术[5],具有较强的闭环性能,在工业应用中取得了令人瞩目的成果[6].结合ILC和MPC 的优点,构造迭代学习模型预测控制(Iterative learning model predictive control,ILMPC)成为解决批次过程控制问题的有效方法[7].在过去十几年间,ILMPC 理论得到了长足的发展.控制模型由易于推导的输入输出模型[8-9],推广到二维状态空间模型[10-11],学习机制也得到了诸多改善[12],衍生了许多解决不确定性、随机扰动、变参考轨迹等具体问题的ILMPC 算法[13-15].

在实际生产中,存在许多具有快动态的批次过程,如工业机器人[16]、运载工具[17]以及部分化学反应器[18].这些批次过程的采样时间通常为秒级甚至毫秒级,对控制器的计算效率提出了较高要求.由于实际批次过程具有较强的非线性,传统的ILMPC需要在每个采样时刻求解复杂的非凸序列二次规划(Sequence quadratic programming,SQP)[19]问题,导致在线计算负担较大,寻优时间较长.通过线性化方法获得更为简单的线性模型,可以有效提高优化求解的速度.轨迹线性化方法将非线性系统沿参考轨迹在每个采样点上进行线性化,得到相应的线性时变(Linear time varying,LTV)模型,将轨迹跟踪问题转化为跟踪误差调节问题[20].其线性化误差可以通过李普希兹条件转化为预测状态误差,从而可获得真实跟踪误差的上界.将此上界作为优化目标函数,就能够在提高控制效率的同时保证系统的跟踪精度.

传统MPC 结构中,在每个采样时刻需要求解整个控制时域内的输入变量序列,其优化问题的自由度为控制输入维数与控制时域长度的乘积.复杂工业过程中,被控系统通常是多输入系统,且需要选取较长的控制时域以保证跟踪性能,所以传统MPC 的在线优化问题自由度较大,计算负担较重.相比较而言,预测函数控制(Predictive functional control,PFC)[21]作为第三代模型预测控制技术,在提高计算效率方面具有突出优势.它将控制输入表示为几个基函数的加权和,从而将复杂的输入序列求解问题转化为更为简单的权重系数求解问题,有效降低待优化变量的维数,减小计算负担.在时域上结合PFC 算法,构建一类特殊结构的迭代学习模型预测控制,即迭代学习预测函数控制(Iterative learning predictive functional control,ILPFC),可以实现对快速批次过程的高效控制[22].但是,随着计算效率的提高,采用PFC 算法同时也会带来可行域缩减的问题,可能会导致控制输入最优性的下降,进而影响系统的跟踪精度.针对此问题,可以通过选择合适的基函数结构,使最优解包含于ILPFC 的可行域内,来确保ILPFC 的跟踪精度.从而实现计算效率和跟踪精度间的平衡.

除了保证控制系统高效性与准确性,如何在时域和迭代域上都实现良好的闭环性能也是ILMPC设计中的一个关键问题.ILMPC 具有典型的二维控制结构,其中MPC 沿时间轴实施滚动时域优化,ILC 沿批次轴通过学习过程数据提高跟踪精度.因此需要同时保证时域稳定性以及迭代收敛性.本文所构建的ILMPC 针对线性化误差问题,构造真实跟踪误差的上界为优化目标函数.该目标函数可以代表实际非线性系统的跟踪误差能量,在稳定性分析中充当Lyapunov 函数.进而,本文所设计的ILMPC非线性控制系统的稳定性可以通过引入终端约束集[23]来保证.但由于LTV 预测模型的采用,经典终端约束集理论中的稳定性条件需要相应地扩展为时变的形式.基于ILMPC 的二维结构,可以从时域稳定性推导出迭代收敛性.

本文首先针对非线性批次过程,基于轨迹线性化模型构建一种具有终端约束的ILMPC 策略,采用真实跟踪误差的范数上界作为优化目标函数.在此基础上,通过引入特殊结构的MPC,即PFC 算法,建立一种高效稳定的ILPFC 策略,实现对非线性批次过程的快速、精确的轨迹跟踪控制.在二维框架下,基于Lyapunov 稳定性理论定性分析所设计的ILMPC/ILPFC 算法的稳定性和收敛性问题.通过无人车及典型快速间歇反应器的仿真验证了所提出ILPFC 策略的有效性.

1 二维模型

1.1 非线性系统轨迹线性化

批次过程可描述为以下非线性离散状态空间模型

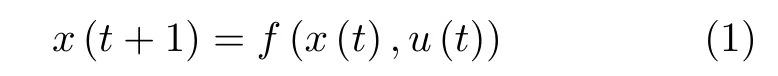
其中,u∈U为nu×1 维的控制输入,x∈X为nx×1 维的状态向量.且对于任意x∈X和u ∈U,f(x(t),u(t)) 满足局部李普希兹连续性条件,其李普希兹常数为Lu,t∈[0,N],N为批次长度.

假设状态参考轨迹为xr,ur为xr对应的参考输入轨迹,满足

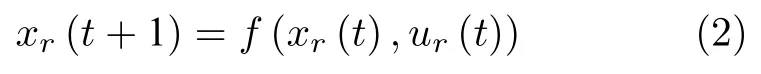
定义状态误差xe(t),输入误差ue(t) 为

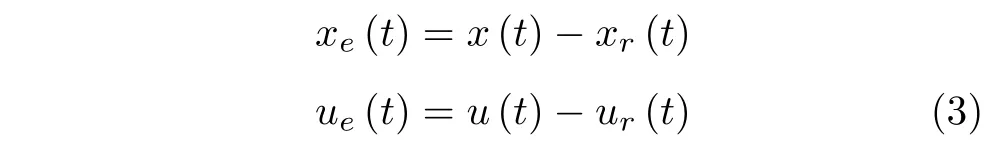
将式(3)代入式(1),可得

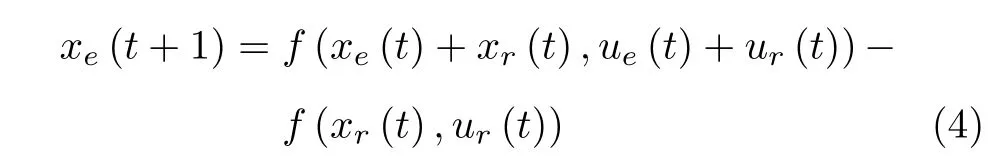
非线性系统(1)的轨迹跟踪问题可转化为系统(4)的零点调节问题.利用泰勒展开法将非线性系统(4)沿参考轨迹线性化,即在 (xe,ue)=0 点处线性化,可得

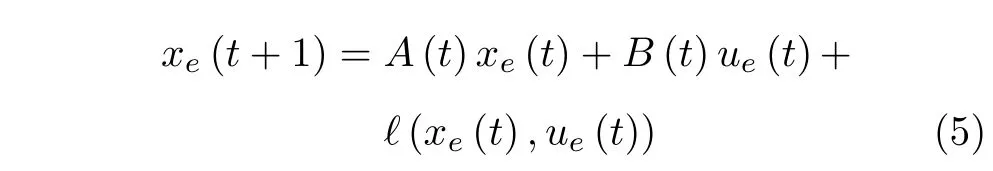
其中,ℓ(xe(t),ue(t)) 代表线性化产生的高阶项.

将式(4)代入式(5),可得

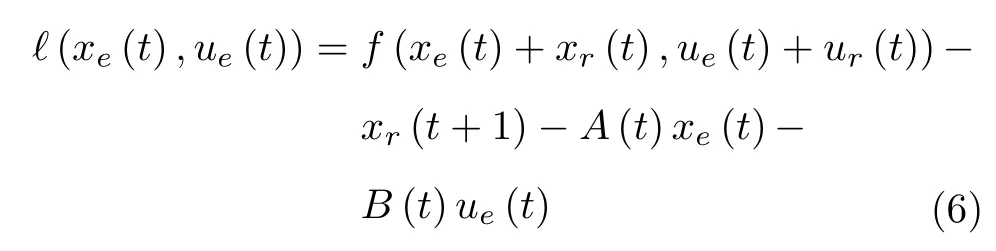
由于f(x(t),u(t)) 满足利普希兹连续条件,所以ℓ(xe(t),ue(t)) 满足

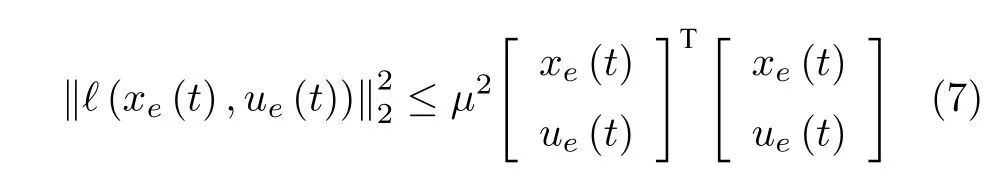
1.2 二维预测模型

假设k代表过程批次,将式(5)在批次k和批次k+1 间做差,可得到如下沿迭代轴的增量模型:

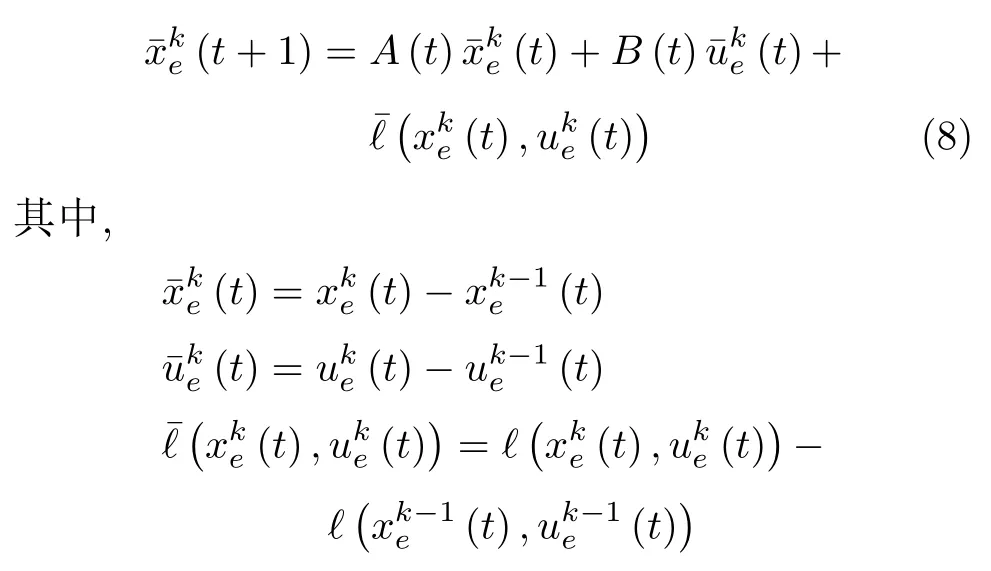
当系统状态x(t) 无限接近参考轨迹xr(t) 时,ℓ(xe(t),ue(t)) 为无穷小量.也就是说,在每个采样点周围存在图1 所示的小邻域,在这些邻域中非线性系统(8)的动态特性可由线性时变系统

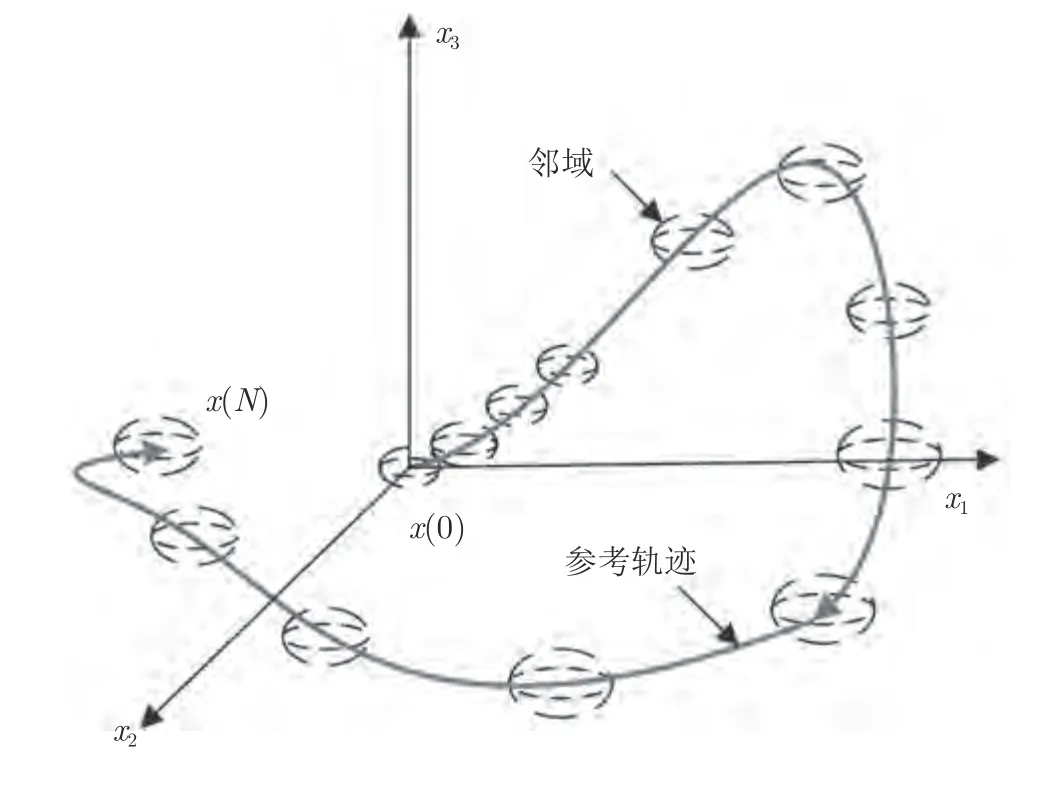
图1 参考轨迹邻域示意图Fig.1 The neighborhoods along reference trajectory

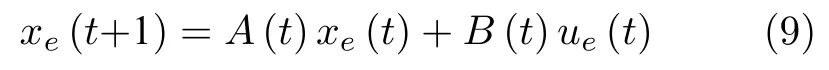
描述.

根据线性时变系统(9)构建线性预测模型

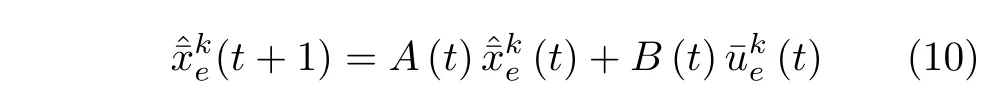
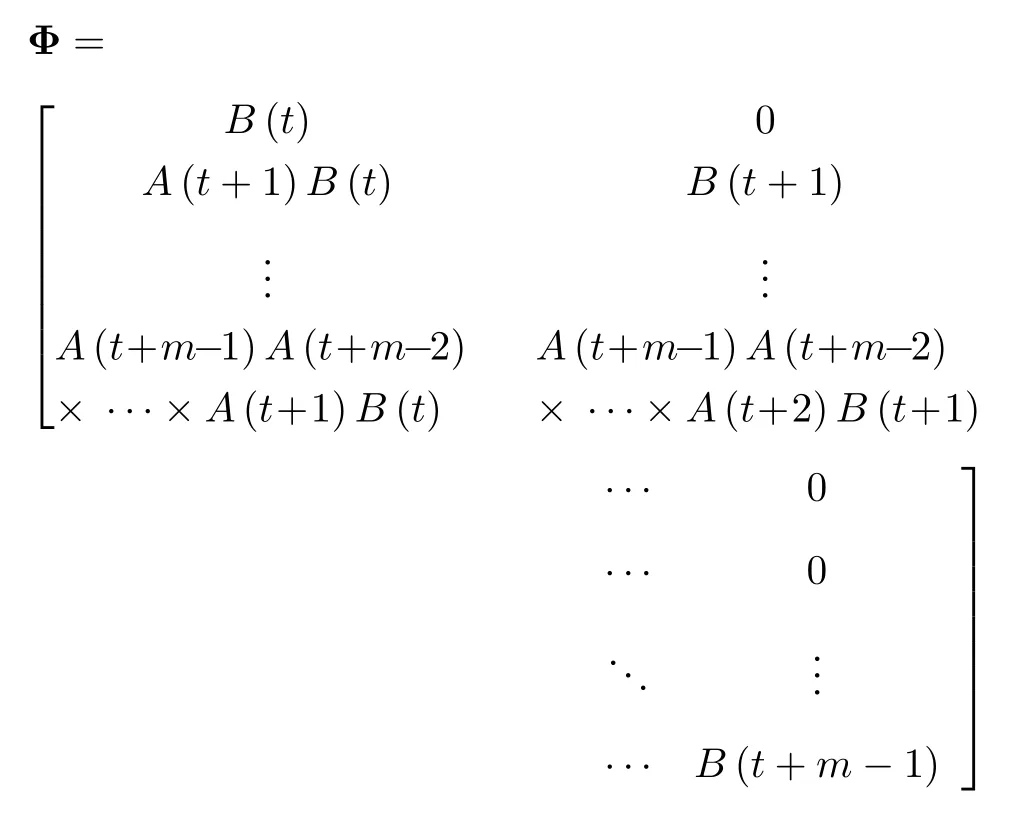
2 稳定ILMPC 策略

2.1 ILMPC 问题描述

注 1.线性矩阵不等式 (26)和(27)可在批次过程开始前离线求解,因而满足快动态系统高效控制的要求.

2.2 ILMPC 约束处理

ILMPC 系统中存在着物理约束及终端约束.为采用SQP 方法对优化问题P1 求解,需要将所有约束转化为标准形式.其中,状态约束处理需要先通过利普希兹条件建立系统真实状态与当前控制输入的关系.

2.2.1 控制输入约束

在批次过程中,控制输入的约束可描述为

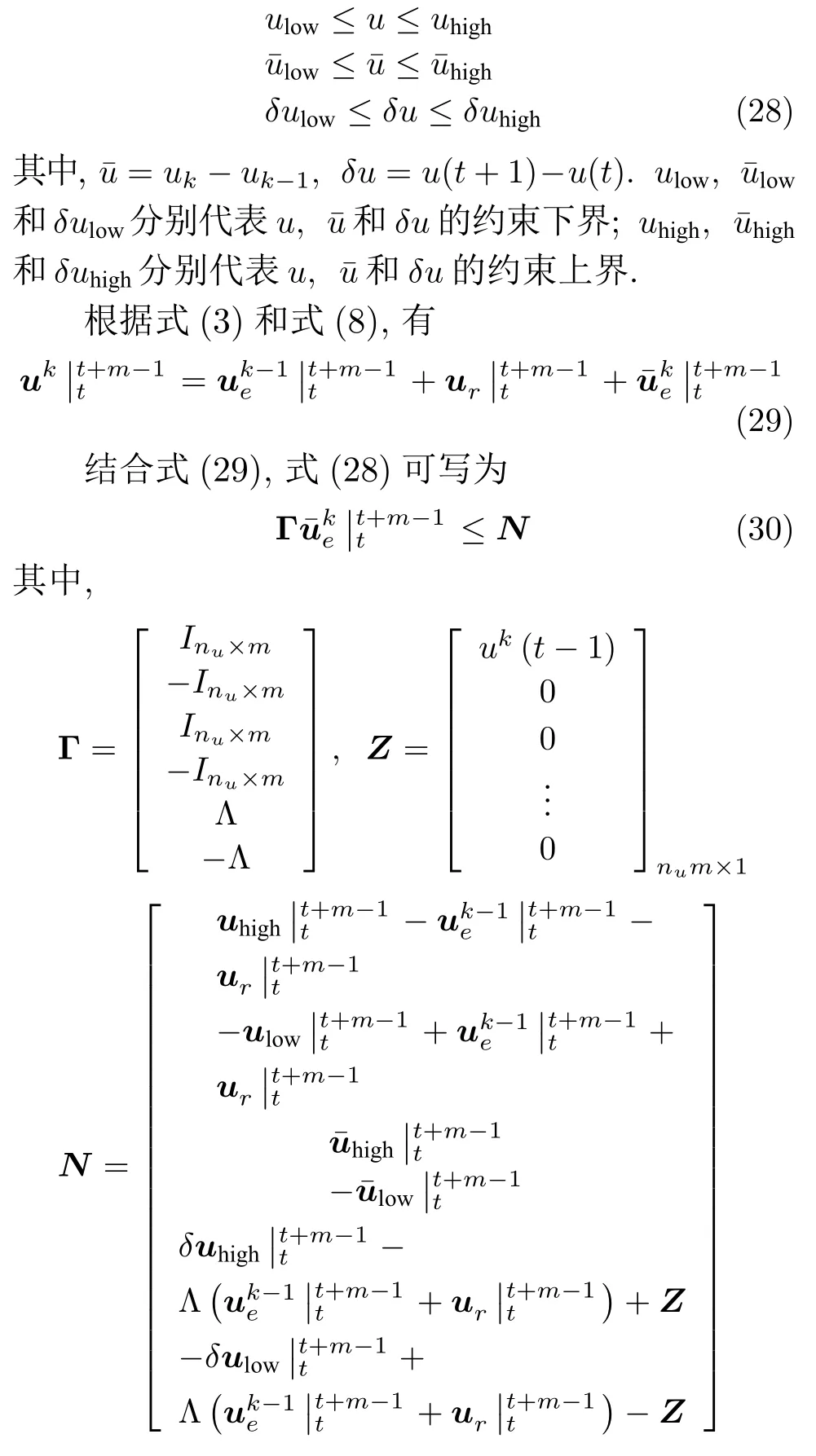
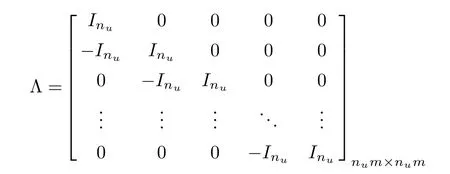
通过将输入约束转化为式(30)的标准形式,优化问题(19)可以利用MATLAB 软件中的SQP 方法直接求解.

2.2.2 状态约束

假设在t时刻对于i=1,2,···,m存在以下状态约束

3 高效ILPFC 策略

3.1 ILPFC 问题描述

实际工业过程通常为复杂多输入多输出系统,需要选取较长的控制时域来保证控制性能,这导致了每个采样时刻的待优化变量维数很大,加重了ILMPC 的计算负担,使其无法达到快速批次过程对计算效率的要求.预测函数控制(PFC)是一类具有特殊控制输入结构的MPC 策略.它将控制量设定为一组视系统特性及参考轨迹形式而定的基函数的线性组合[21].系统输出预报值通过基函数的已知响应合成,因而,只需通过优化计算求出基函数的线性加权系数即可获得控制输入量.鉴于其计算量小、控制精度高的优点,PFC 已广泛应用于液压机器人[25]、导弹控制系统[26]等快速工业过程.在ILMPC 的时域控制中采用PFC 构建高效的ILPFC 算法,能够在保持跟踪精度的前提下,进一步提高控制效率.

注 2.经典预测函数控制中基函数的选取通常依赖于目标参考轨迹形式及系统内部动态特性.针对批次过程轨迹跟踪问题,本文提出一种新的基函数构造方法.首先根据目标参考轨迹及前一批次的信息反馈,选取随时间和批次变化的基函数η1=起主要调节作用;然后再针对系统偏差情况及扰动形式,结合系统动态特性确定其他基函数η2,···,ηb起补偿作用.由于基函数为上一批次的控制输入偏差,若系统不存在外界扰动或状态偏差,选取即可实现高精度跟踪.当系统存在状态偏差时,可以通过选取冲激信号和阶跃信号作为基函数在η1的基础上进行调整[26],补偿状态偏差,达到高精度跟踪;当系统存在外界扰动时,为在系统最后输出中去除该扰动的影响,应根据扰动类型及系统内部特性,反推出能够抑制该种扰动的基函数类型,进行扰动补偿.例如,若外部扰动为正弦形式,系统具有线性动态,为消除扰动影响,应选择正弦形式的基函数以补偿扰动,保证跟踪精度.

进而,ILPFC 的优化问题可描述为

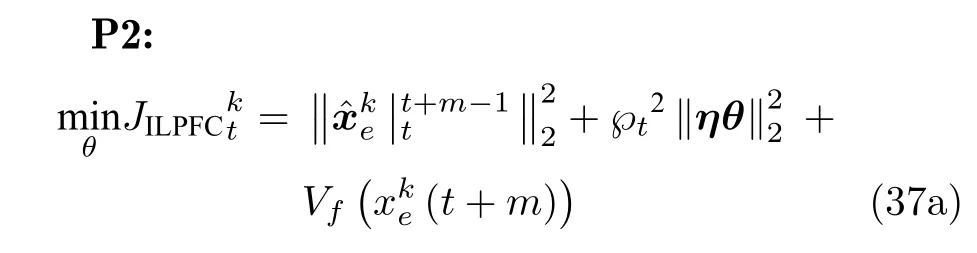
满足

3.2 ILPFC 性能分析

从本质上讲,在利用SQP 求解带约束优化问题时,其计算复杂度与优化问题的自由度紧密相关[19],这可以通过SQP 求解的迭代寻优过程进行具体说明.

当使用SQP 求解ILPFC 优化问题P2 时,需建立对应的拉格朗日函数

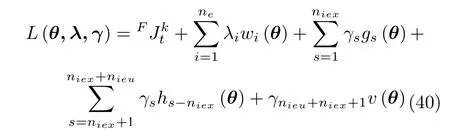
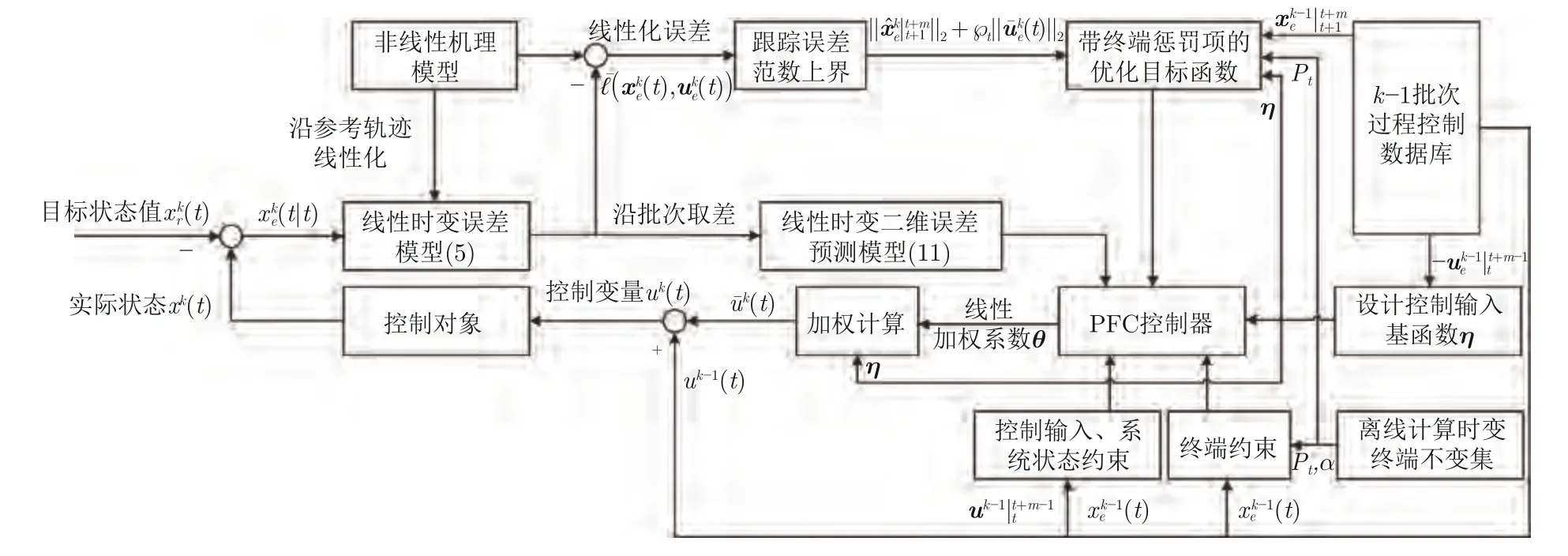
图2 ILPFC 控制框图Fig.2 The control scheme of the ILPFC

易知ILPFC 优化问题P2 中,Hessian 矩阵的维数为b×b.而未采用PFC 的ILMPC 优化问题P1 中,Hessian 矩阵为

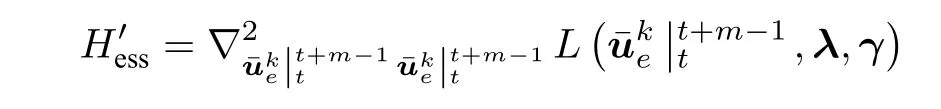
其维数为num×num.在实际应用中,被控对象通常为多输入多输出系统,且控制时域m较大,导致num通常量级较大.相比较而言,ILPFC 中只需根据参考轨迹及系统特性选择少数几个基函数来达成控制目标,即b的量级通常较小.所以P2 的Hessian 矩阵的维数会远远小于P1,也就是说ILPFC 滚动优化求解的计算量远小于ILMPC.

尽管ILPFC 通过应用PFC 结构提高了计算效率,但也相应地带来了可行域减小的问题.ILMPC的原可行域为所有满足约束的控制向量构成的区域,可描述为而在ILPFC 中由于控制输入由基函数的加权和代替,其可行域缩减为 ΘILMPC内一个b维的区域,可表示为 ΘILPFC={ηθ|x ∈X,u ∈U,(t+m)∈Ωt+m,θ ∈Rb}中的全局最优解不包含于缩减后的可行域 ΘILPFC,那么ILPFC 的优化解只是局部最优解,进而会对ILPFC 的跟踪精度带来负面影响.

为了实现计算效率和跟踪精度的平衡,在ILPFC 设计中选择合适的基函数使其可行域 ΘILPFC仍能覆盖全局最优解尤为关键.针对这个问题,选取一种随时间和批次变化的基函数结构:首先根据上一批次的控制经验选取基函数,使ILPFC 可行域靠近最优解;再根据系统中的状态偏移或者扰动形式选择典型信号作为其他基函数进行补偿调整,使得以所有基函数为基的空间覆盖最优解.为形象描述这个过程,以单输入、控制时域为3、基函数个数为2 的ILPFC 系统为例进行说明,其可行域形成过程示于图3.其中三维椭球区域为ILMPC的可行域 ΘILMPC,则ILPFC 的可行域 ΘILPFC为基函数构成的二维平面与该椭球的相交面.

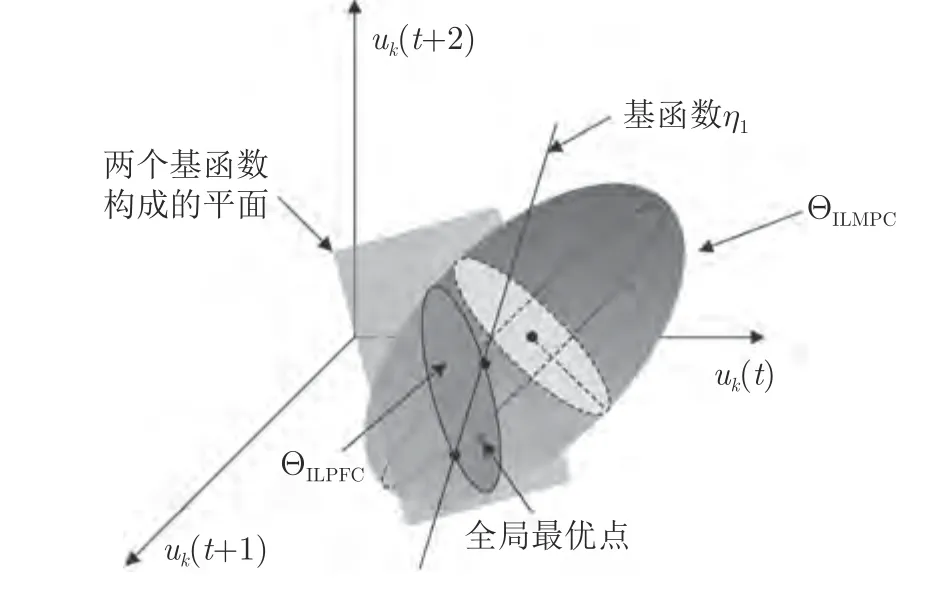
图3 ILPFC 可行域形成过程Fig.3 The forming process of feasible region of ILPFC

由于基函数η1是根据参考轨迹及系统动态选择的随时间和批次变化的基函数,它会形成一条与全局最优解十分接近的直线.通过选择另一典型信号基函数对此直线的移动方向进行简单调整,即可使η1与η2构成的平面区域包含全局最优解(图中圆点),那么该平面与椭球的相交面,即ILPFC 可行域 ΘILPFC必定能包含全局最优解.

结合第3 节中的ILMPC 稳定性结论,可由图3总结出:

1) 若合理选择基函数使其构成的区域与ILMPC的可行域相交,那么ILPFC 优化问题在任意未来时刻可行;

4 ILPFC/ILMPC 收敛性分析

收敛性是衡量ILMPC 算法性能及维护控制系统安全的重要性质[8-11].ILMPC 算法的收敛性通常定义为跟踪误差沿迭代次序k收敛.现有的ILMPC 算法大多未考虑控制系统时域稳定问题,所以通常需要满足一些较为苛刻的条件以保证迭代收敛性[8,10].本文所提出的ILPFC 算法将真实跟踪误差的二范数上界作为优化目标函数,并加入终端约束来保证系统时域稳定性.结合第3 节中引理1的稳定性结论,ILPFC 的收敛性可以在合理假设下通过 “三步推导”证得.首先根据闭环稳定性可推出跟踪误差有界性;然后,通过反证法可以得到初始控制输入的收敛性.最后重复利用利普希兹条件,证得系统跟踪误差沿迭代轴收敛.

定理 2.若初始状态满足则ILPFC(ILMPC)系统的跟踪误差沿迭代轴收敛.

证明.1)证明跟踪误差的有界性,由式(37)可知,ILPFC 中第k批次初始时刻的目标函数为

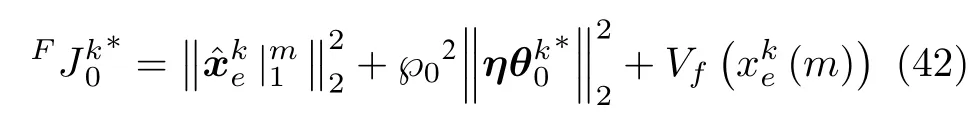
5 仿真研究

5.1 无人地面车辆

无人地面车辆(Unmanned ground vehicle,UGV)是广泛应用于农业、物流业、采矿业、军事的移动式人工智能车辆.在执行巡逻、运输及农耕任务时,其控制目标可看作自动重复跟踪给定的运动轨迹,是一类典型的快速批次过程,采样间隔较短.其非线性动态特性可由以下微分方程描述[27]

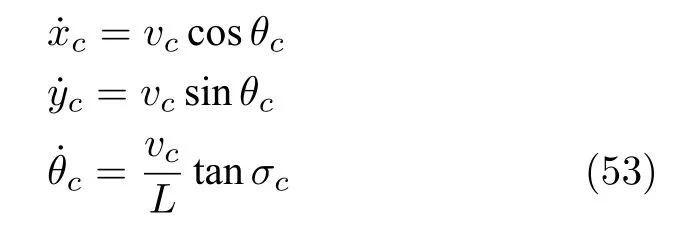
其中,xc和yc为车辆在笛卡尔坐标系下的位置坐标,θc表示车辆轴线中心的方向,L=1.2 m 为车轮的轴距,vc代表车辆速度,σc代表车辆转向输入.[xcycθc]T为车辆控制系统的状态变量,[vcσc]T为控制系统的输入变量.车辆参考轨迹为

采样时间选为0.2 s.车辆初始状态为 [10.3 9.5 1]T,与参考轨迹相比存在初始状态偏移.每一批次的初始状态保持一致,即满足定理2 中的收敛条件选取初始批次控制输入为已知的参考输入轨迹vr和σr.

控制输入约束及状态约束设为

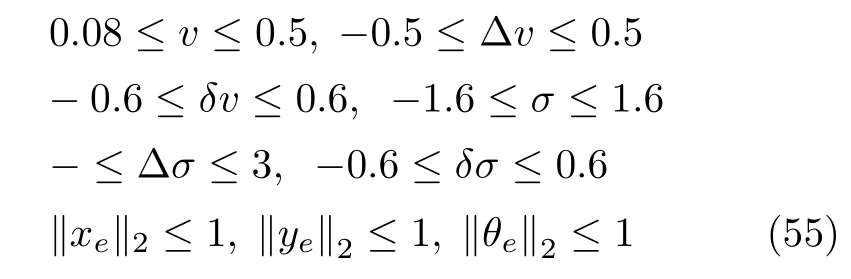
其中,xe=xc-xr,ye=yc-yr,θe=θc-θr.

离散化非线性系统(53),并沿参考轨迹(54)实施线性化,建立如式(5)的线性化误差模型

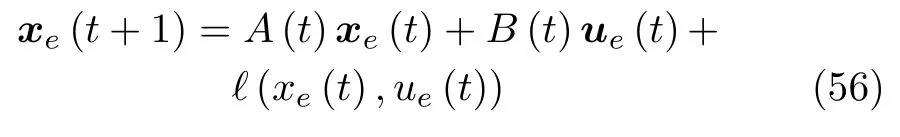
其中,

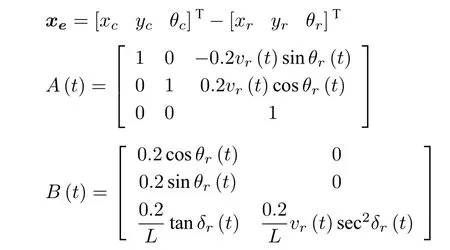
ℓ(xe(t),ue(t)) 代表泰勒展开的高阶项.

基于式(5)～(11),由线性化模型(56)形成二维预测模型,其中预测时域与控制时域都选为20.利用李普希兹条件,得到真实跟踪误差的上界其中时变李普希兹权重℘t可以通过式(16)离线计算得到.将此上界作为优化目标函数,结合终端约束,构造ILMPC 优化问题P1,其中,Pt+m,K(t)和α由式(26)和式(27)表示的线性矩阵不等式计算得到.求解得到的跟踪误差时变终端不变集,如图4 所示.

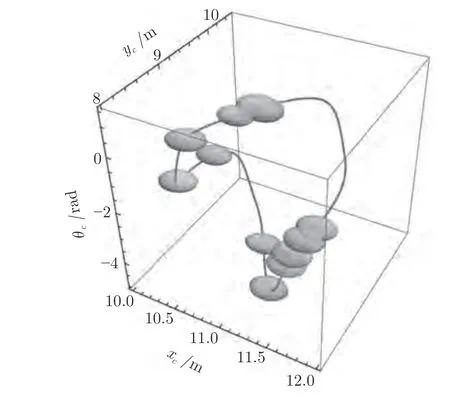
图4 UGV 系统跟踪误差时变终端不变集Fig.4 The time-varying tracking error terminal invariant set of UGV control system

在ILPFC 中,选取基函数

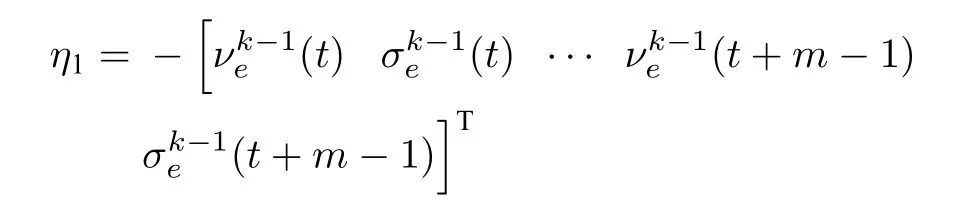
η2为单位阶跃信号.将控制输入变量表示成基函数η1和η2的加权和,构成ILPFC 优化问题P2.在每个采样时刻,控制输入的求解空间为nu×m(2×20)维,随时间和批次变化的基函数η1于其中形成一条接近最优解的曲线,通过单位阶跃基函数η2的调整,η1和η2构成与ILMPC 可行域 ΘILMPC相交的二维区域,保证LPFC 优化问题的可行.其相交区域,即ILPFC 的可行域 ΘILPFC包含令的控制输入,以保证ILPFC 控制系统稳定.仿真得到的状态及控制输入曲线分别如图5和图6 所示,表明ILPFC 能够以较高精度跟踪参考轨迹.图7(a)显示了第2 批次中基函数权重系数(θ1,θ2)随时间变化的轨迹,表明ILPFC 优化问题在所有采样时刻可行.图7(b)为跟踪误差均方差(Main square error,MSE) 随批次的变化曲线,验证了ILPFC 系统跟踪误差的收敛性.

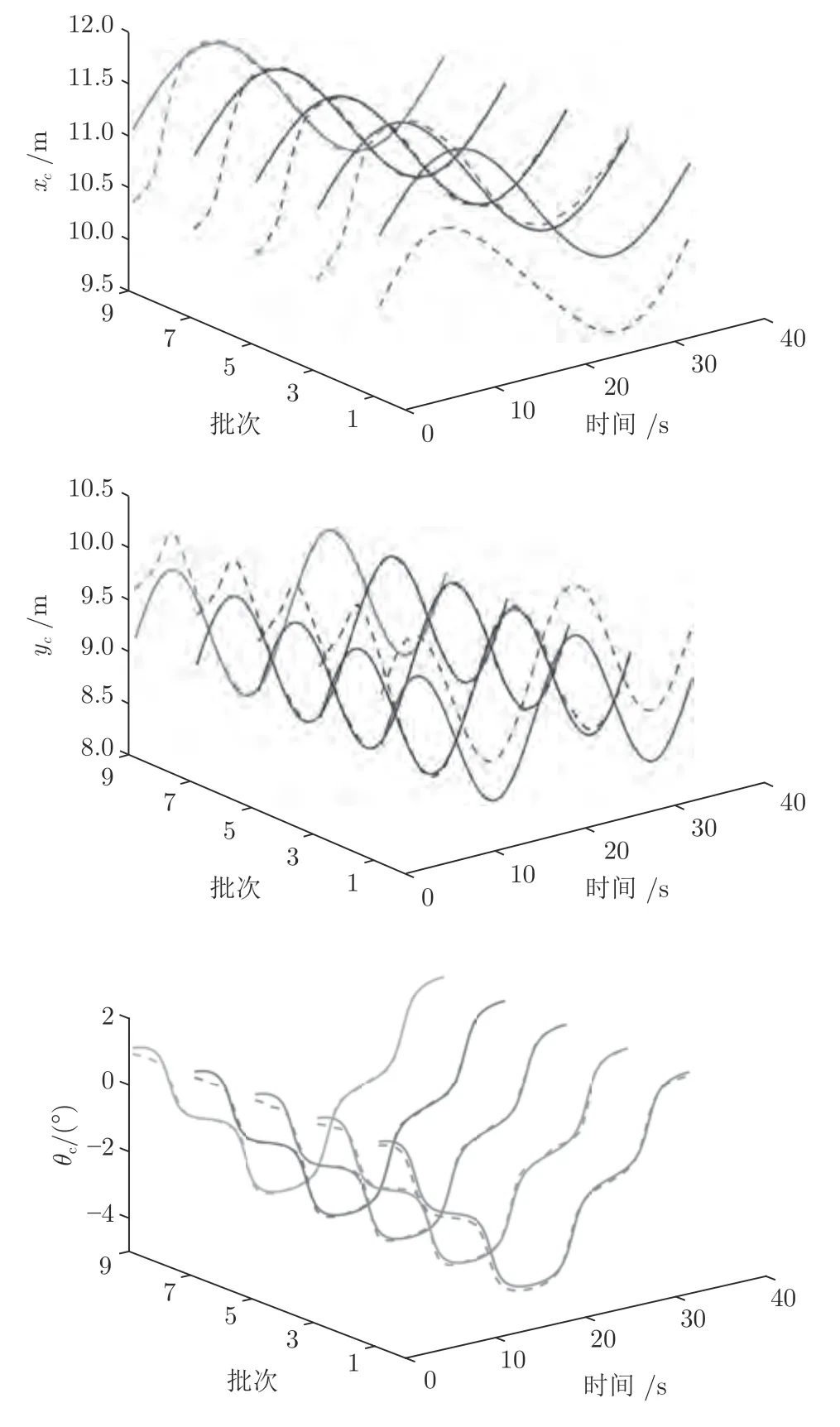
图5 ILPFC 控制下状态跟踪曲线Fig.5 The state tracking trajectories under the ILPFC

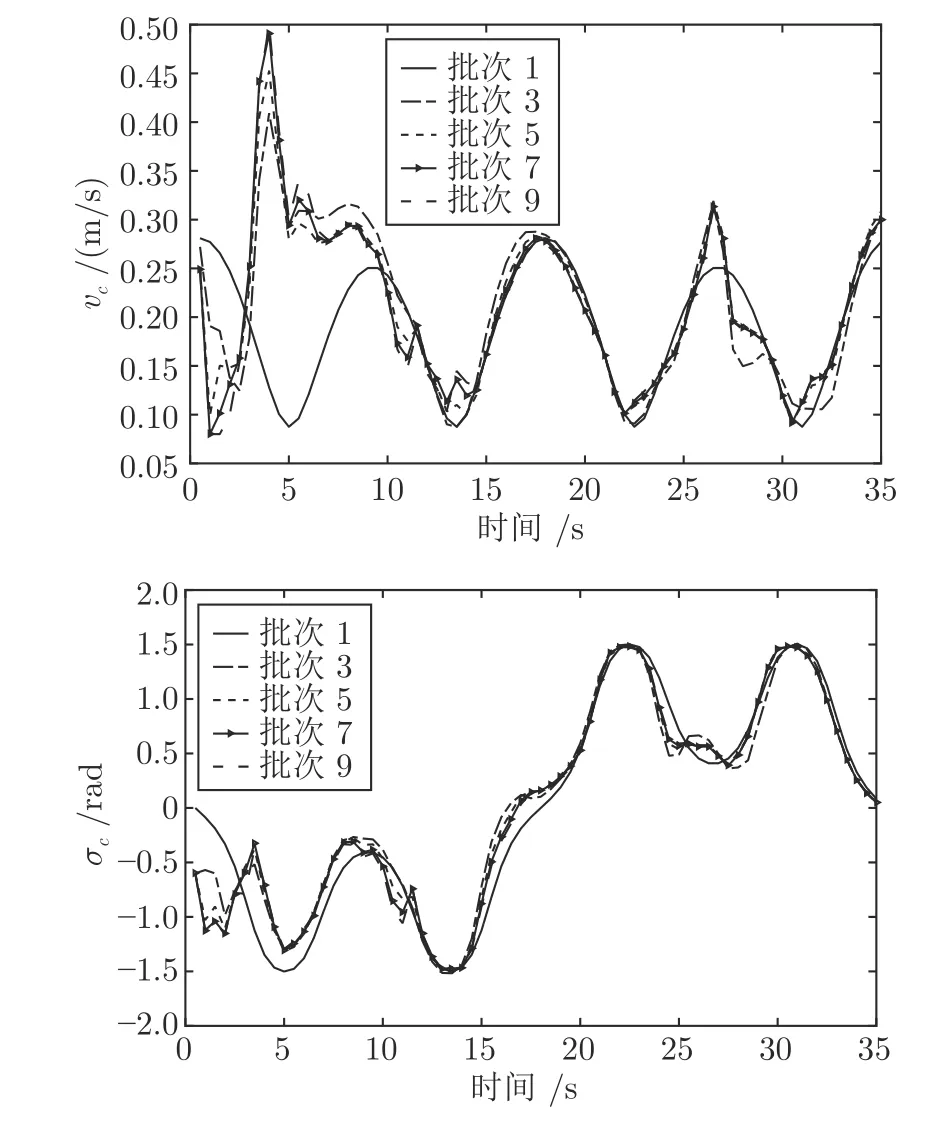
图6 ILPFC 控制下控制输入曲线Fig.6 The trajectories of control inputs under the ILPFC

图7 UGV 系统 θ 变化曲线和MSE 变化曲线Fig.7 The change curves of θ and MSE of UGV control system

多点ILMPC (Multi-point ILMPC,mp-ILMPC)[11]是一种在解决非线性问题上具有突出优势的算法,已在国际学术界获得广泛认可.它采用工作点线性化得到的线性定常预测模型,利用多点信息进行加权预测,同样以真实跟踪误差的上界作为目标函数

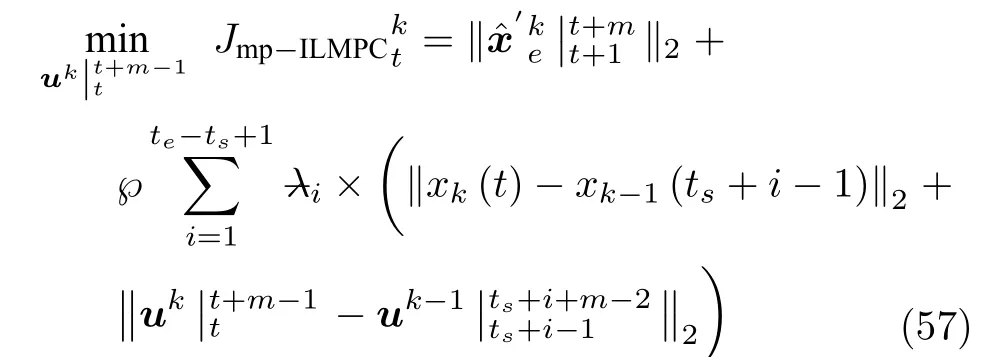
为了验证ILPFC 算法的有效性,将其与ILMPC (P1)以及mp-ILMPC 从计算效率和跟踪精度两个角度进行仿真实验对比.图8 描述了三种控制策略下第9 批次的无人车运动曲线,表明ILPFC 在跟踪精度上与ILMPC和mp-ILMPC 相当.设置预测/控制时域分别为10,15和20,重复进行仿真实验,从平均计算时间和平均跟踪误差均方差两个方面对三种控制器进行性能分析,相关结果如表1 所示.随预测/控制时域增加,三种方法的平均MSE 都呈下降趋势,使得跟踪精度提高.但是与此同时,ILMPC和mp-ILMPC 的平均计算时间均有显著增长,并在控制时域达到20 时超过了采样间隔.而ILPFC 的在线计算负担几乎保持不变,始终维持较高的控制效率.这是由于ILPFC 与其他两种方法相比优化复杂度更低.当控制时域变长时,由于采用特殊的控制输入结构,ILPFC 优化问题(P1)的Hessian 矩阵维数保持为 2×2,使在线计算负担较低.而ILMPC 的Hessian 矩阵维数迅速增长,计算负担也随之加重.在mp-ILMPC 中,在每个采样时刻需要求解非凸优化问题,使得其计算时间相对较长,并随控制时域增加而增长.综上,与其他两种策略相比较,ILPFC 能更好地实现计算效率与控制最优性间的平衡.

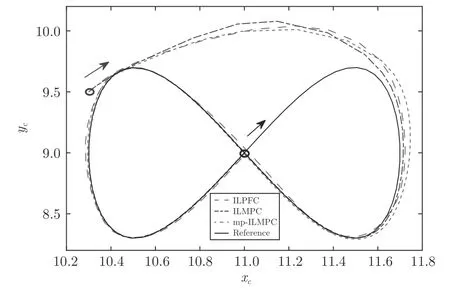
图8 UGV 系统分别在ILPFC、ILMPC和mp-ILMPC控制下第9 批次的运动跟踪曲线Fig.8 The motion curve of UGV during the 9th batch under the ILPFC,ILMPC and mp-ILMPC

表1 ILPFC、ILMPC 及mp-ILMPC 计算量和跟踪误差比较Table 1 The comparison of computation time and tracking errors between ILPFC,ILMPC and mp-ILMPC

5.2 非线性间歇反应器

化学工业中存在很多快速反应过程[18],要求在较短的采样时间内计算出控制输入,这对此类间歇反应器的实时控制提出了很高的要求.本组仿真实验通过对快速间歇反应器的温度控制,验证ILPFC 在提高优化效率方面的作用.反应器中进行由反应物A生成反应物B的二级放热反应[28],其控制任务为通过调节冷却套温度来重复跟踪给定的反应温度曲线.反应过程的非线性动态可由以下微分方程描述

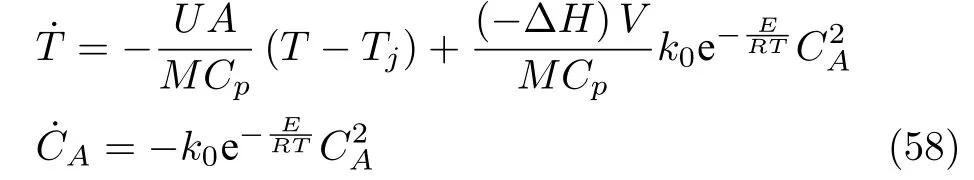
其中,T为反应温度,CA为反应物A浓度,Tj为冷却剂温度,其他参数物理意义可参见文献[28].各参数取值为

采样时间为0.02 min.参考轨迹采用文献[28]的典型生产过程反应温度曲线.反应器系统存在初始状态偏移,实际初始状态在所有批次保持为[CA0,T0]T=[0.9(mol/l),296.15(K)],满足定理2 中的收敛条件.选取初始批次控制输入为已知的参考输入轨迹ur,系统约束为

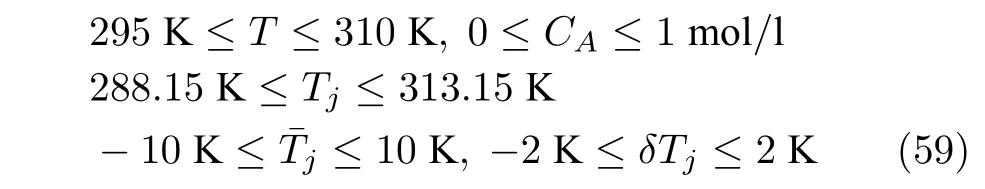
针对非线性系统(58)实施离散化,并沿参考轨迹进行线性化,得到如式(11)的二维预测模型,其中预测/控制时域选为20.由此带来的线性化误差通过时变李普希兹权重℘t在优化目标函数中加以补偿.再结合终端约束,构建ILMPC 优化问题P1,其中时变终端不变集由式(26)和式(27)表示的线性矩阵不等式计算得到,如图9 所示.

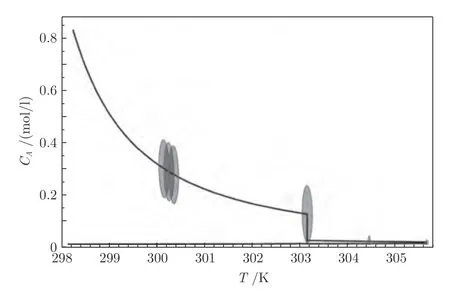
图9 间歇反应器系统跟踪误差时变终端不变集Fig.9 The time-varying tracking error terminal invariant set of batch reactor control system

在ILPFC 优化问题P2 中,选取基函数η1=,η2为单位阶跃信号,η3为单位斜坡信号.这3 个基函数构成的区域可与ILMPC 的可行域相交并覆盖最优解,以此保证ILPFC 的递归可行性及闭环稳定性.ILMPC 控制下的仿真结果如图10～ 12 所示,表明ILPFC 能够以较高精度跟踪设定的反应器温度参考轨迹.图13(a)显示了第20 批次基函数权重系数θ1,θ2和θ3沿时间的变化轨迹,证明ILPFC 优化问题P2 的可行性.图13(b)为跟踪误差MSE 沿批次的变化轨迹,表明ILPFC 系统的跟踪误差沿迭代收敛.

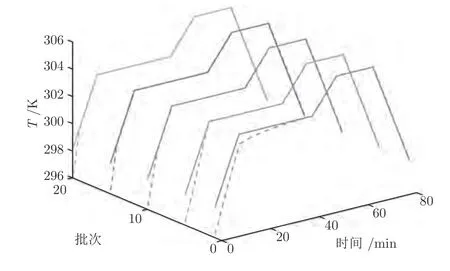
图10 ILPFC 控制下反应温度跟踪曲线Fig.10 The trajectories of the reaction temperature T under the ILPFC

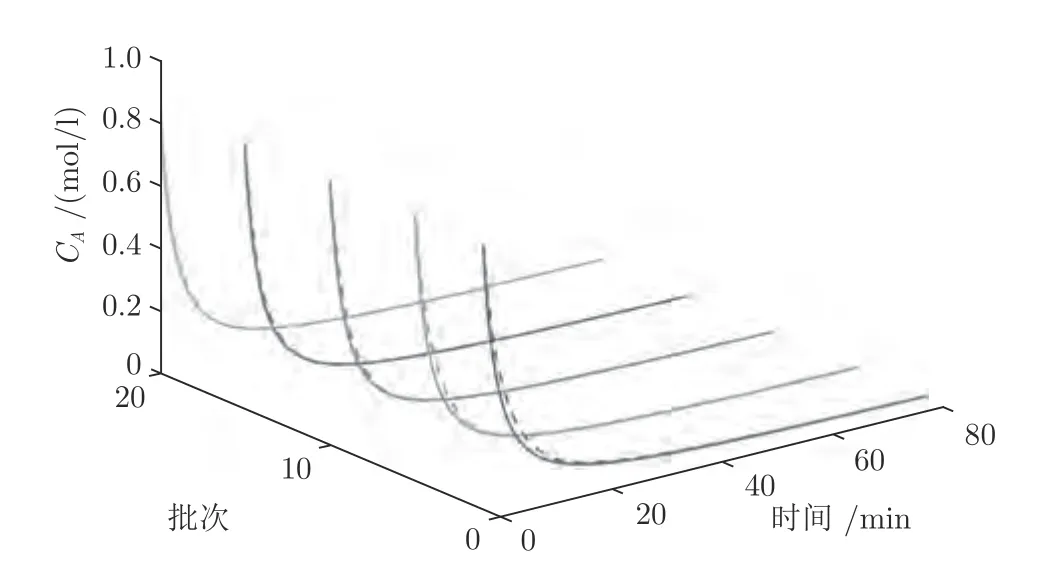
图11 ILPFC 控制下反应物A 浓度跟踪曲线Fig.11 The trajectories of the concentration CA under the ILPFC

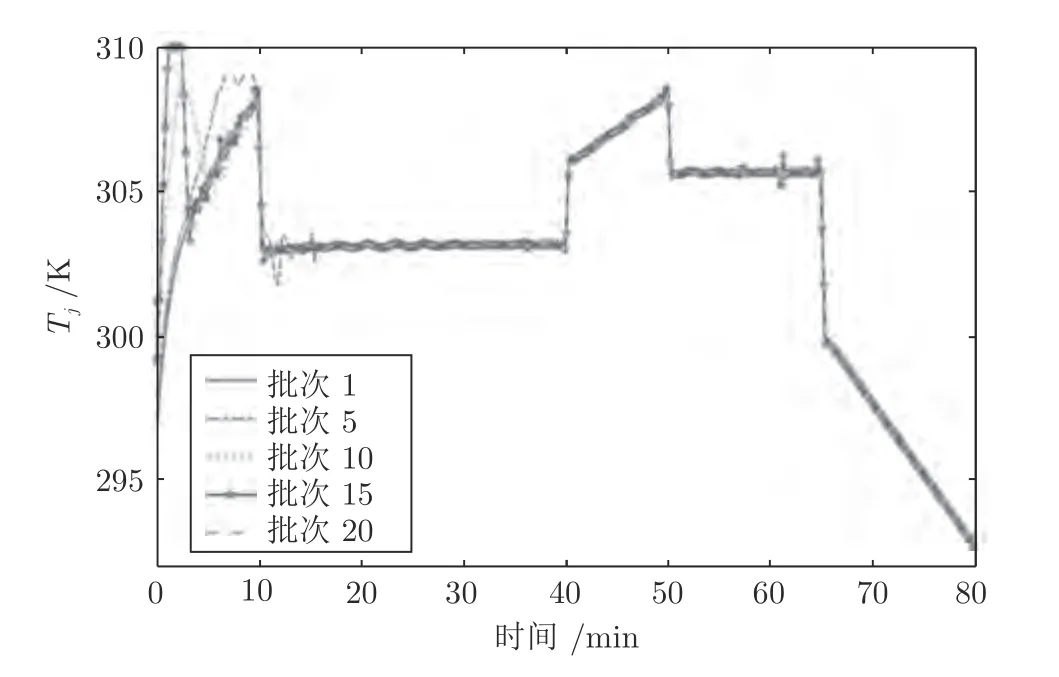
图12 ILPFC 控制下冷却剂温度曲线Fig.12 The trajectories of the coolant stream temperature Tj under the ILPFC

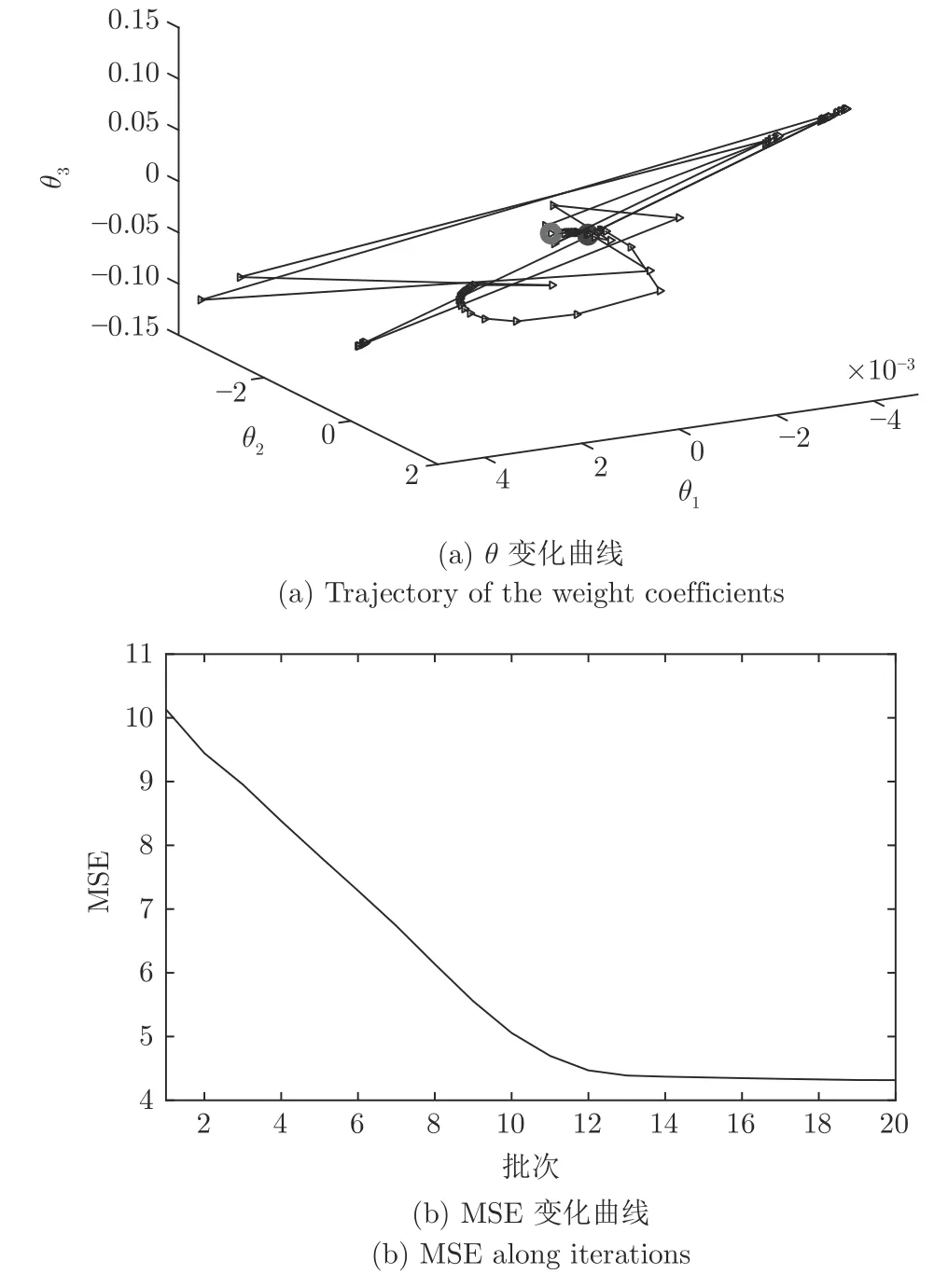
图13 间歇反应器系统 θ 变化曲线和MSE 变化曲线Fig.13 The change curves of θ and MSE of batch reactor control system

为了验证ILPFC 的跟踪性能,对ILPFC、ILMPC 以及mp-ILMPC 控制下的反应温度跟踪曲线进行比较,如图14 所示.其中,mp-ILMPC 中的参数设置为对比结果表明ILPFC 的跟踪精度与ILMPC 相差无几.选取预测/控制时域分别为10,15和20 重复进行仿真实验,从平均计算时间及平均跟踪误差MSE 两个角度比较三种方法,其结果如表2 所示.很明显,随着预测/控制时域增大,三种控制方法的跟踪精度均提高.但是,只有ILPFC 保持了较高的求解效率,其他两种方法的计算效率均呈现下降趋势.

表2 ILPFC、ILMPC 及mp-ILMPC 计算量和跟踪误差比较Table 2 The comparison of computation time and tracking errors between ILPFC,ILMPC and mp-ILMPC

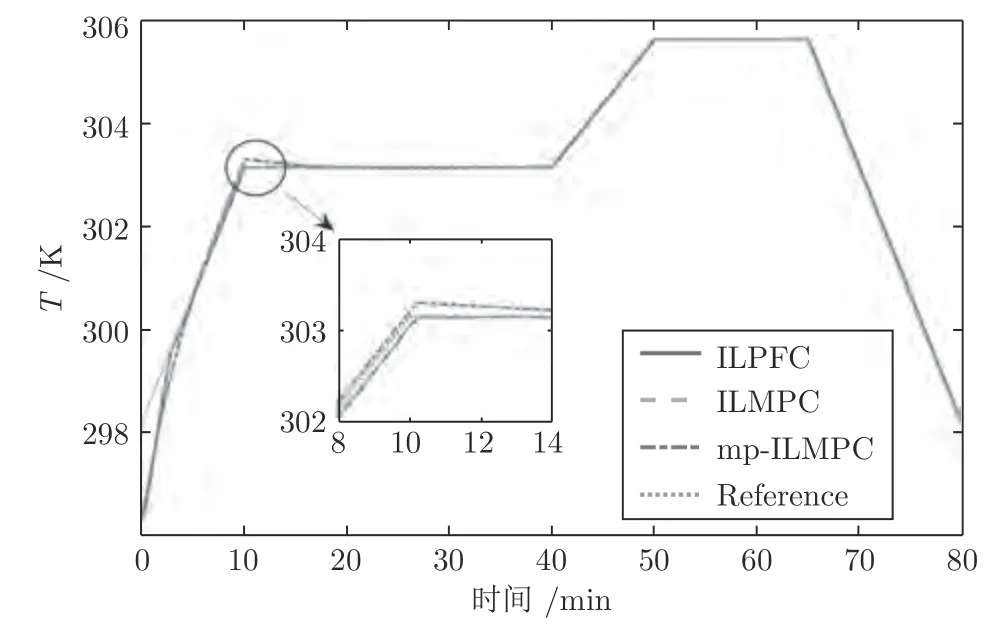
图14 第20 批次ILPFC、ILMPC和mp-ILMPC控制下反应温度跟踪曲线Fig.14 The tracking trajectories of the reaction temprature under the ILPFC,ILMPC and mp-ILMPC in the 20th batch

在进行非线性批次过程轨迹线性化时,参考输入轨迹ur是已知的.在系统存在初始状态偏差的情况下,ur较为接近目标控制输入轨迹.因此将ur作为初始批次的控制输入是最优的选择.图15 描述了初始批次输入轨迹为303 K 幅值阶跃信号时的跟踪曲线.可以看出,在初始控制输入轨迹严重偏离目标输入轨迹时,ILPFC 仍能在10 个批次内实现高精度跟踪,验证了ILPFC 对初始批次输入的鲁棒性.

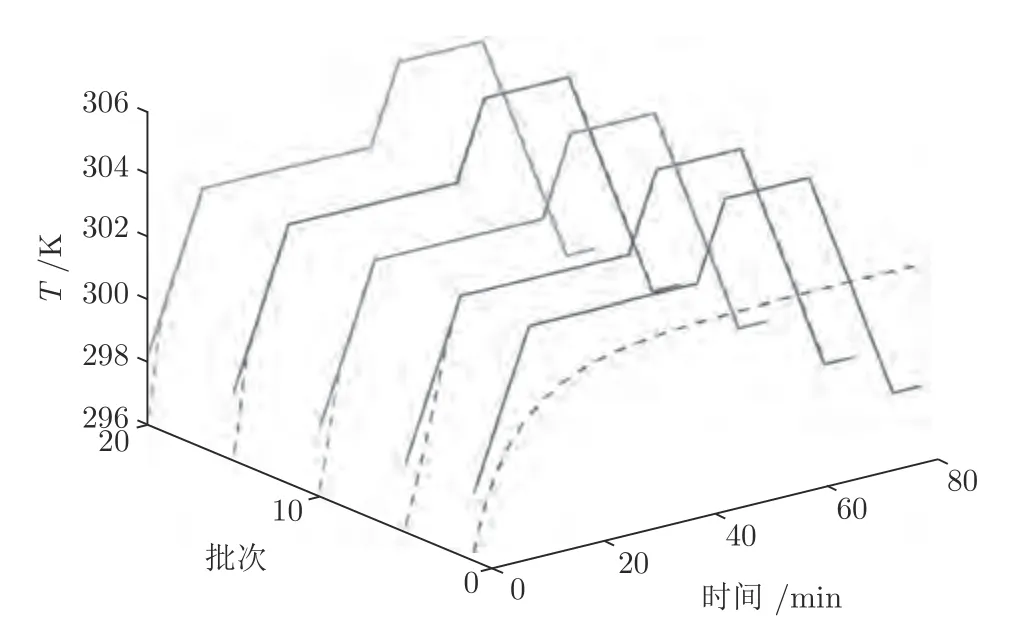
图15 阶跃初始批次输入下ILPFC 温度跟踪曲线Fig.15 The tracking trajectories of the reaction temprature T under the ILPFC with a step input in the initial batch

综上,ILPFC 实现了高精度跟踪与高效优化求解之间的平衡,这对提高快速间歇反应器的产品质量和生产效率都具有显著的实际意义.

6 结束语

本文基于二维ILMPC 框架,在时域控制中结合PFC 算法来降低优化计算负担,由此带来的可行域缩减问题在一定程度上会影响ILPFC 的跟踪精度.通过选择一种随时间和批次变化的特殊基函数结构,可使在缩减的可行域内仍能获得最优解,达到了控制效率与跟踪精度间的平衡.针对UGV系统和快速间歇反应器的仿真实验验证了ILPFC 算法的有效性.

通过对ILPFC 算法结构的剖析,可以发现其控制性能与所选择的基函数品质密切相关.因此,如何获得系统的最优基函数是未来研究的一个重要方向.基于批次过程大数据,可以发展一种沿迭代轴进行基函数自学习的控制框架,这将有利于进一步提高ILPFC 系统的学习能力及闭环性能.

附录A 定理1 的证明