有界扰动下约束非线性系统鲁棒经济模型预测控制

何德峰 韩 平 王青松

近年来,经济模型预测控制(Economic model predictive control,EMPC)在工业界和学术界引起了广泛关注[1-2].作为一种新近发展的先进控制技术,EMPC 有望成为解决复杂系统节能、降耗和增效优化控制问题的重要手段,目前已应用于能源、造纸、车辆等系统的能效优化控制[3-9].除具有常规模型预测控制 (Model predictive control,MPC)的显式处理约束和多变量控制的优点外,EMPC 还能优化 “经济”类目标函数,通常这类函数不是设定值跟踪偏差的正定函数,而是系统状态和控制变量的非凸或非正定函数[1-9].因此,把以设定值跟踪偏差的正定函数为优化目标的常规MPC 称为目标跟踪MPC,而不以跟踪偏差的正定函数为优化目标的MPC 统称为经济MPC[2].现有研究表明:经济最优性目标与闭环系统的稳定性目标具有一定的冲突性[1-2],因此近年来EMPC 的稳定性综合策略得到了广泛研究.

为建立EMPC 关于经济平衡点的稳定性,一种主要方法是构造基于经济优化目标函数的Lyapunov 函数[5,10-17].例如,使用终端等式约束和强对偶性假设,定义经济目标函数的旋转代价函数并将其作为闭环系统的一个Lyapunov 函数[10],而引入广义终端等式约束[15],建立了经济性能变化下的递推可行性与闭环系统的有界稳定性[11].进一步,采用严格耗散性条件、终端不等式约束和终端代价函数代替,降低了EMPC 稳定性综合策略的保守性[12-13].在无终端约束EMPC 策略中,闭环轨迹在足够长的预测时域情况下收敛到平衡点的邻域[16-17].虽然无终端约束增大了闭环系统的吸引域,但长时域预测将大大增加了在线优化的计算负担.进一步,EMPC稳定性和经济性是一对存在冲突的控制目标[18-19],且稳定性和经济性目标无法统一度量,难以通过权重标定.对此,从多目标优化控制角度,考虑非线性系统强对偶性或耗散性条件难以满足情况,文献[20-21]通过构造稳定性收缩约束,建立闭环系统关于最优经济平衡点的渐近稳定性.

实际系统总是存在不确定扰动,现有EMPC 策略通常难以保证受扰系统的可行性和稳定性.对于目标跟踪MPC,目前已有较多鲁棒稳定性结果[22-32],主要包括本质鲁棒MPC[22]、Tube 鲁棒MPC[24-25]以及min-max MPC[26-32]等,其中min-max MPC 采用微分对策原理,在使最坏扰动输入情况下系统的性能指标上界达到最小.相比于本质鲁棒MPC和Tube 鲁棒MPC,min-max MPC 能大大降低鲁棒MPC 的保守性,但会增加优化问题的在线计算量[1].为降低min-max MPC 的在线计算量,文献[30]采用仿射输入结构,使MPC 含有抑制扰动的闭环成分和易于求解的开环优化.另一方面,输入到状态稳定性(Input-to-state stability,ISS)成为分析不确定系统鲁棒稳定性的一个有效工具[23,27-32],并应用到了EMPC 鲁棒性研究,如文献[33-34]采用强对偶性假设和约束紧缩方法,证明了周期性扰动下线性系统EMPC 闭环收敛性,文献[35]获得了非线性系统EMPC 的有界稳定性结果,提高了经济性能优化的灵活性,文献[36]将稳定性目标和经济性目标相加,证明EMPC 线性系统关于经济目标的最大值是ISS 的,文献[37]施加保证鲁棒稳定性的显式收缩约束,提出两种非线性系统鲁棒EMPC算法,文献[38]提出Lipschitz连续非线性系统的隐式收缩鲁棒EMPC 策略,提高了系统的平均经济性能.

本文针对含有未知有界扰动的不确定非线性系统,提出一种新的具有递推可行性以及ISS 保证的鲁棒EMPC 策略.该策略明确考虑经济最优性和鲁棒稳定性控制目标的矛盾特点,采用微分对策原理在线滚动优化计算这对冲突目标的min-max 问题.离线计算最优经济平衡点,并利用状态与该平衡点的偏差定义鲁棒稳定性目标函数,而经济目标函数则由系统的经济性能给定.通过特殊设计EMPC 优化问题的隐式收缩约束,并在鲁棒稳定性目标优化问题中引入一个新约束,保证EMPC 优化的递推可行性和闭环系统关于不确定扰动输入的ISS.相比现有鲁棒EMPC 策略,本文首先建立了约束非线性系统具有ISS 的鲁棒EMPC 策略;其次,EMPC 递推可行性和鲁棒稳定性无需强对偶性或耗散性假设条件,从而扩大了鲁棒 EMPC 的应用范围;最后,采用微分对策原理得到了保守性更低的容许扰动上界.采用一个受扰非线性连续搅拌釜反应器(Continuous stirred tank reactor,CSTR)的仿真实例,验证本文提出策略的有效性与优越性.

符号说明:Z+表示非负整数集,Ia:b表示集合{i ∈Z+:a ≤i ≤b,a ∈Z+,b ∈Z+},I≥j表示集合{i ∈Z+:i ≥j,j ∈Z+}.x+表示x的下一时刻状态,|x|表示x的欧几里得范数,‖x‖=sup{|x(k)|,k ∈Z+},x(i|k) 表示在第k时刻对未来第k+i时刻的预测变量.连续函数h1:R+→R+称为K类函数系指该函数单调递增,且h1(0)=0 ;函数h2:R+→R+称为K∞类 函数系指该函数是K类函数,且当s →∞时,有h(s)→∞;函数h3:R+×R+→R+称为KL函 数系指对于任意固定的t≥0,h3(·,t) 是K类函数,而对于任意固定的s＞0,h3(s,·) 是单调递减,且当t→∞时,h3(s,t)→0 .

1 问题描述

考虑不确定离散时间非线性系统

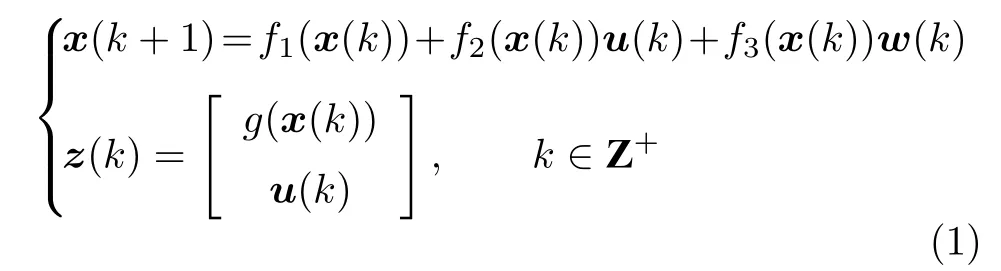
其中,x(k)∈Rn,u(k)∈Rm,w(k)∈Rq和z(k)∈Rs分别表示系统在k时刻的状态、控制输入、扰动输入和辅助输出.假设f1(·),f2(·),f3(·)和g(·) 分别为定义在 Rn上的光滑函数,满足f1(0)=0,f2(0)=0,f3(0)=0 以及g(0)=0 .系统(1) 在k时刻的状态x(k)=φ(k;x0,u,w) 由初始状态x0,控制序列u={u(0),u(1),···}和扰动序列w={w(0),w(1),···}表示.假设系统(1)的状态完全可测,且系统状态和控制输入满足约束

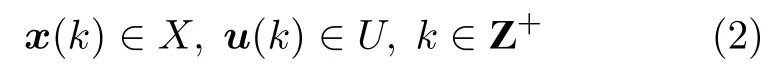
其中,集合X⊂Rn和U⊂Rm均为凸的紧集,且它们内部包含某些平衡点 (xe,ue) .

假设 1.扰动输入w满足如下约束

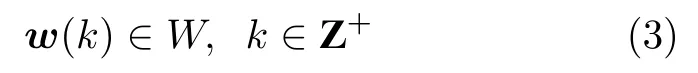
其中,W为包含平衡点 (xe,ue) 的紧集.满足约束(3)的扰动称为容许扰动.注意w表示参数不确定性、模型失配以及持续外部扰动等多种有界不确定性[29],其上界表示为‖w‖=sup{|wt|:wt∈W,t ∈Z+}.

考虑系统(1)的经济性能函数Le:X×U →R,基于系统(1)的名义模型x+=f1(x)+f2(x)u离线计算如下最优经济平衡点

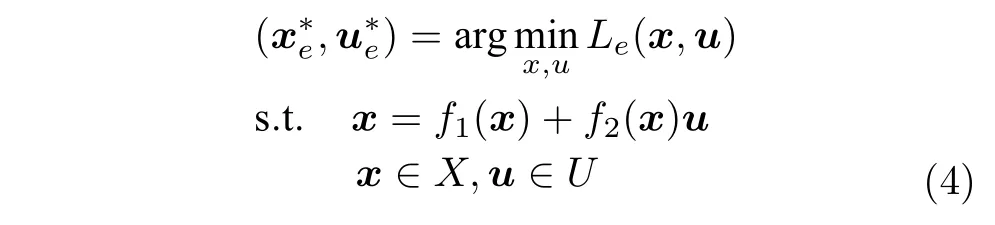
不失一般性,后文假设系统(1)的最优经济平衡点为原点.

下面介绍输入到状态稳定(ISS)相关理论,首先回顾鲁棒不变集的概念.考虑一般离散不确定非线性系统x+=f(x,w) .

定义 1[27].考虑系统x+=f(x,w)和集 Θ⊆Rn,如果对于任意x∈Θ和w∈W,该系统满足x+=f(x,w)∈Θ,则称 Θ 为该系统的一个鲁棒不变集.

定义 2[27].考虑系统x+=f(x,w) 及其内含原点的鲁棒不变集 Θ⊆X,如果对于任意初始状态x0∈Θ 及w∈W,存在K∞类函数α和KL类函数β使系统满足

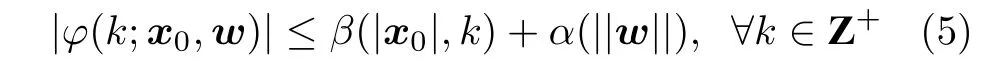
则该系统在 Θ 内是ISS 的.

引理 1[29].考虑系统x+=f(x,w) 及其内含原点的鲁棒不变集 Θ⊆X,如果对于任意x∈Θ和w ∈W,存在连续函数V:Rn→R+满足

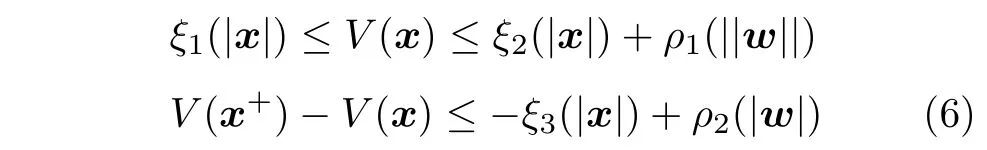
其中,ξ1,ξ2和ξ3为K∞类函数,ρ1和ρ2为K类函数,则该系统在 Θ 内ISS,称V为该系统的ISSLyapunov 函数.

注 1.由定义2 可知,当系统不受扰动或仅受衰减扰动作用时,系统最终在原点处渐近稳定;当受持续有界扰动作用时,系统有界稳定,且状态轨迹最终收敛的范围与持续扰动的上界有关.

本文目标是针对不确定非线性系统(1),通过极小化经济性能函数在线计算鲁棒EMPC 控制器,要求相应闭环系统满足约束条件(2),且闭环系统的最优经济平衡点相对于容许扰动(3)具有ISS.

2 鲁棒经济模型预测控制

考虑有限预测步长N∈I≥1,定义k∈Z+时刻的N步控制序列u(k)={u(0|k),u(1|k),···,u(N-1|k)}、扰动序列w(k)={w(0|k),w(1|k),···,w(N-1|k)}以及对应的预测状态序列x(k)={x(1|k),x(2|k),···,x(N|k)},并且x(i|k)=φ(i;x(k),u(k),w(k)),其中x(k) 为当前时刻系统状态.考虑系统(1)的经济性能函数Le,定义N步经济目标函数

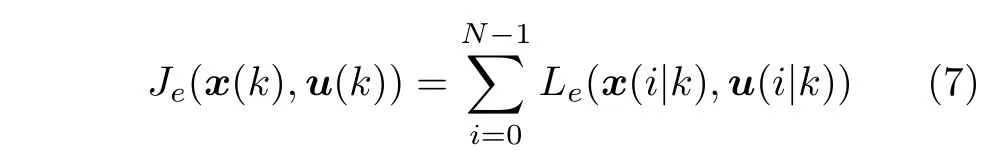
其中,x(0|k)=x(k)

为计算鲁棒EMPC 控制器,在每个时刻优化经济目标函数(7).由于扰动的存在,在鲁棒EMPC 中求解如下min-max 经济最优控制问题:

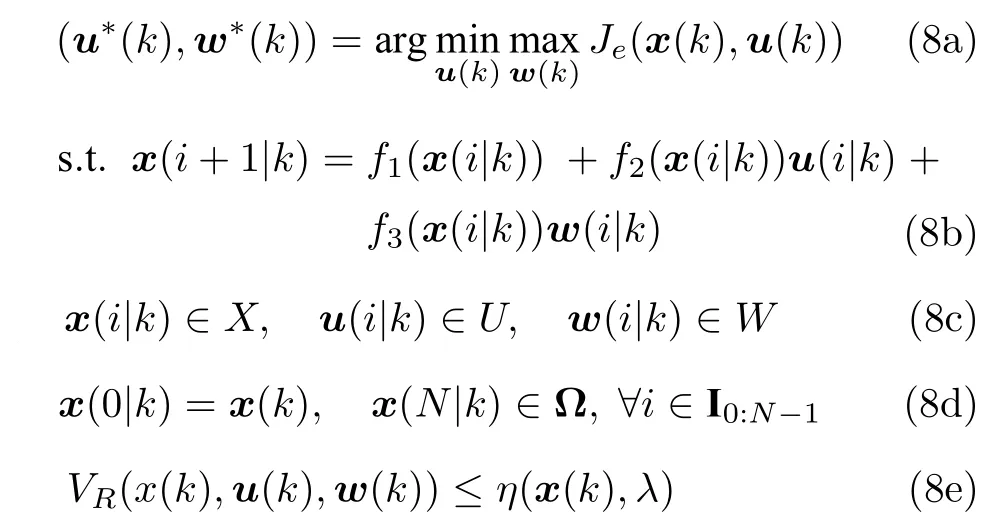
其中,(u*(k),w*(k)) 为k时刻的经济最优解,对应最优预测状态序列x*(k) ;x(0|k)=x(k) 为初始条件;x(N|k)∈Ω 为终端状态约束,终端约束集 Ω⊂X且内含原点;(8e)为待设计的鲁棒稳定性收缩约束,λ∈[0,1) 为收缩因子.进一步定义如下关于最优经济平衡点的鲁棒稳定性目标函数:

其中,函数L:X×U →R+,Lw:W →R+和E:X →R+为连续有界函数.为书写简洁,令VR(x)=VR(x,u,w) .

假设 2.存在K∞类函数αl,αw和βw,使鲁棒稳定性目标函数VR(x) 满足:L(x,u)≥αl(|x|),∀x ∈X,∀u∈U;αw(|w|)≤Lw(w)≤βw(|w|),∀w ∈W.

假设 3.在终端约束集 Ω 内存在局部反馈控制律u=π(x) 使 得π(x)∈U,∀x ∈X和如下不等式成立:

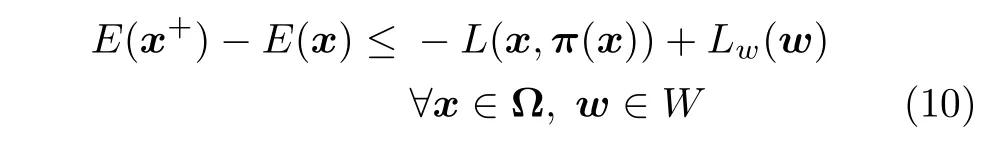
其中,αf(|x|)≤E(x)≤βf(|x|),αf和βf为K∞类函数.

注意,局部控制律u=π(x) 可采用如H∞控制方法求解[26,30].为此,定义对称矩阵

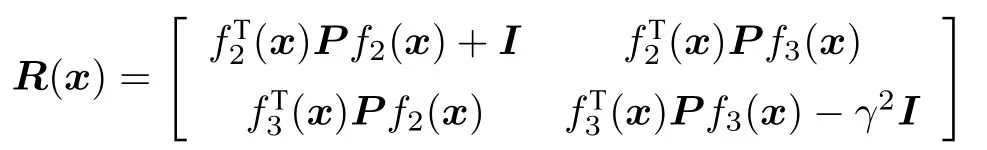
其中,P为对称正定矩阵,I为单位矩阵.令R=R(0) .不失一般性,令扰动抑制水平γ=1 .

引理 2[30].假设矩阵P满足Riccati 不等式方程

注 2.如果假设3 成立,则对于任意w∈W,Ω为闭环系统(13)的一个鲁棒不变集,同时E(x) 为该系统在 Ω 内的一个ISS-Lyapunov 函数.文献[30]给出了保证 Ω 鲁棒不变性的一个充分条件,即容许扰动w的上界

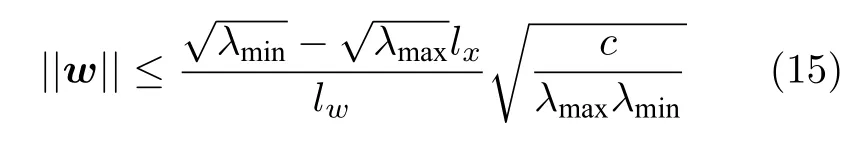
其中,lx和lw分别为闭环系统(13)关于x和w的局部Lipschitz 常数,λmax和λmin分别为矩阵P的最大和最小特征值.如扰动w满足式(15),则 Ω 为闭环系统(13)的鲁棒不变集,且π(x)∈U,∀x ∈Ω .

下面构造收缩约束函数η.令x(k)为当前时刻系统状态,求解如下有限时域鲁棒性最优控制问题

其中,(u*(i|k-1),w*(i|k-1)) 是 优化问题(8)在k-1 时刻最优解 (u*(k-1),w*(k-1)) 的 分量.将 (u*(k-1),w*(k-1))和(u0(k),w0(k)) 分别代入VR(x),据此定义函数

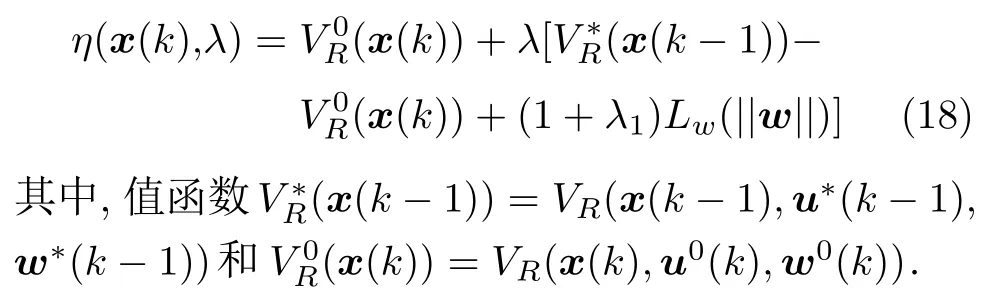
如果优化问题(8)在k时刻可行,则根据滚动时域控制原理,将u*(k) 的第1 个分量定义为鲁棒EMPC 控制律,即u(k)=umpc(x(k))=u*(0|k),对应闭环系统为

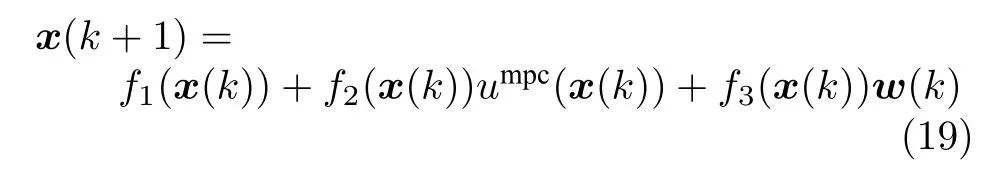
计算鲁棒EMPC 控制器的算法总结如下:

算法 1.鲁棒EMPC 算法

步骤 1.初始化.设定N∈I≥1,λ ∈[0,1),λ1≥1,Le(x,u),L(x,u),Lw(w)和E(x) ;离线计算π(x)以及 Ω ;令k=0,考虑初始状态x0,令η充分大;求解优化问题(8),得到经济最优解 (u*(0),w*(0)),并将u*(0) 的首个分量u*(0|0) 作用于系统(1).

步骤 2.在k时刻,利用k-1 时刻经济最优解(u*(k-1),w*(k-1)) 构 造(u1(k),w1(k)),更 新(16e);求解优化问题(16),得到当前时刻鲁棒最优解 (u0(k),w0(k)) .

步骤 3.计算和,更新η;求解优化问题(8),得到当前时刻经济最优解(u*(k),w*(tk)) .

步骤 4.将u*(k) 的首个分量u*(0|k) 作用于系统(1).

步骤 5.令k=k+1,测量系统(1)的状态;返回步骤2.

为更清晰地描述算法1 的运行过程,图1 给出了每个时刻两个优化问题的求解顺序.

由算法1和图1 可知,在初始时刻k=0,由于约束(8e)不起作用,故在初始时刻无需求解优化问题(16),并可令η(x0,λ)→∞.

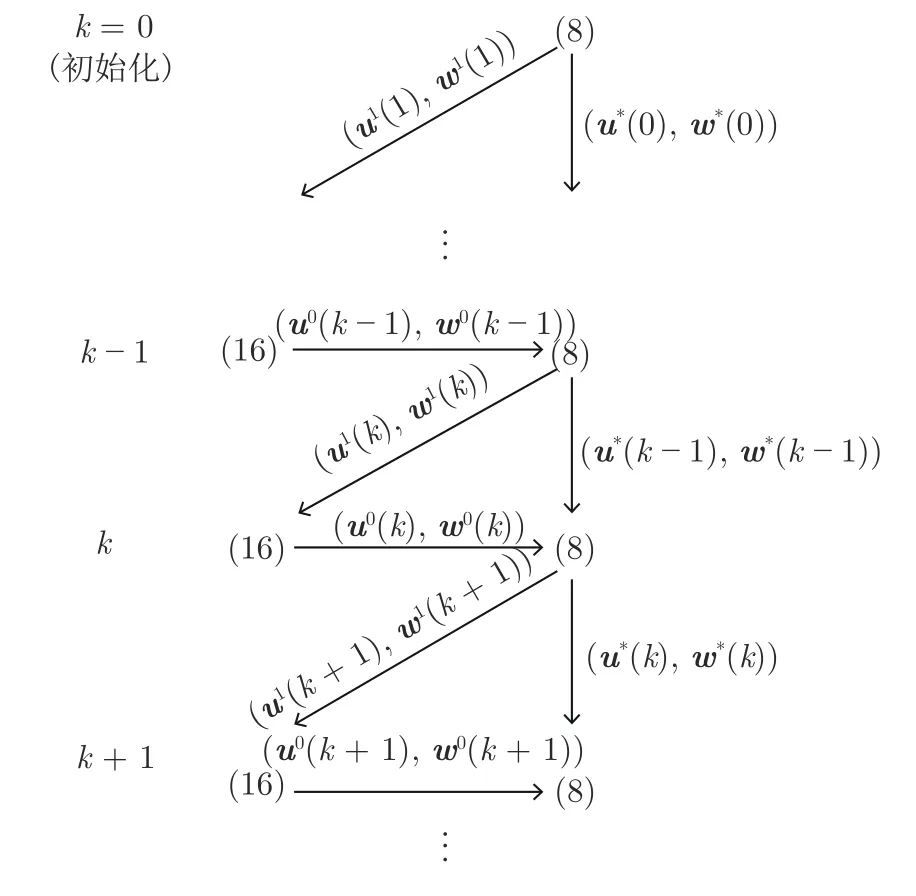
图1 鲁棒EMPC 算法运行过程示意图Fig.1 A schematic diagram of the robust EMPC algorithm

3 输入到状态稳定性

闭环系统(19)具有ISS 性质的前提是需要保证算法1 具有递推可行性,即两个优化问题在每个时刻都至少存在一组可行解(不一定最优),使得对于任意容许扰动,经济优化问题(8)和鲁棒性优化问题(16)的所有约束均满足.注意,(8b)～(8d)与(16b)～(16d)具有相同约束.

考虑约束不确定系统(1)～(3)和状态τ=x(0|k)∈X.对于优化问题(8),定义N步可行控制序列集为

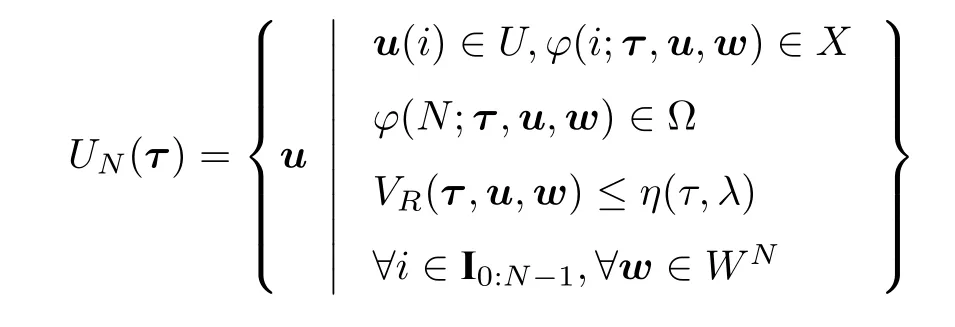
其中,N步扰动约束集WN=W ×W ×···×W.

定义 3.考虑系统(1)和状态τ=x(0|k)∈X,如果可行控制序列集UN(τ) 非空,则称τ为该系统的初始可行状态.所有初始可行状态τ的集合称为系统的初始可行状态集XN.

定理 1.如果假设1～3 成立,且容许扰动满足式(15),则优化问题(16)具有递推可行性.

证明.考虑序列对 (u1(k),w1(k)) 并代入系统(1)得到状态序列x1(k)={x*(1|k-1),···,x*(N|k-1),x1(N|k)},其中x*(N|k-1)∈Ω 是对应于u*(k-1)的终端预测状态.由假设3和注2 可知,Ω 是闭环系统(13)的鲁棒不变集,故对于任意w1(N -1|k)∈W,u1(N -1|k)=π(x*(N|k-1))∈U和x1(N|k)=φ(N;x*(N|k-1),u1(N -1|k),w1(N -1|k))∈Ω 成立.利用序列对 (u1(k),w1(k)) 构造优化问题(16)在k时刻的备选解

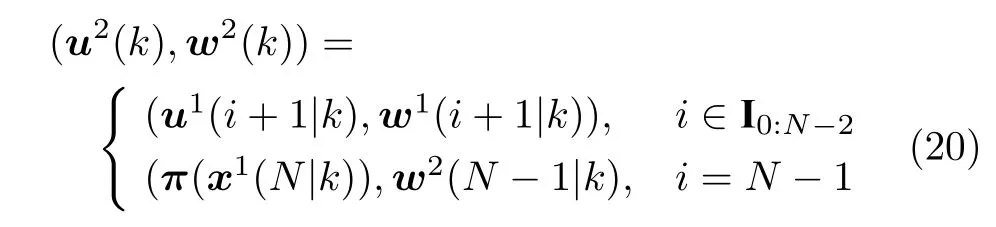
其对应状态序列x2(k)={x1(1|k),···,x1(N|k),x2(N|k)},其中x1(N|k)∈Ω.又 Ω 是鲁棒不变的,则对于任意w2(N -1|k)∈W,u2(N -1|k)=π(x1(N|k))∈U和x2(N|k)=φ(N;x1(N|k),u2(N-1|k),w2(N -1|k))∈Ω 成立,因此约束(16b)～(16d)满足.

再分别 将 (u1(k),w1(k))和(u2(k),w2(k)) 代入函数VR(x) 中,计算得

故约束(16e)满足,从而 (u2(k),w2(k)) 为问题(16)在k时刻的可行解,即优化问题(16)具有递推可行性.□

定理 2.如果假设1～3 成立,且容许扰动满足式(15),则优化问题(8)具有递推可行性.

故约束(8e) 成立.由定理1 可知,(u0(k),w0(k))作为优化问题(16)在k时刻的最优解满足约束(8b)～(8d).因此,在k时刻总存在可行控制序列u0(k) 满足优化问题(8)的所有约束,从而优化问题(8)具有递推可行性.□

根据定理1和定理2,本文鲁棒EMPC 策略中的双目标优化问题皆具有递推可行性.下面将基于定理1和定理2 给出闭环系统(19)的ISS 结果.

定理 3.如果假设1～3 成立,且容许扰动满足式(15),则当优化问题(8)在初始时刻存在可行解时,闭环系统(19)在鲁棒不变集XN内相对于扰动具有ISS.

证明.由定理1和定理2 可知,当优化问题(8)在初始时刻存在可行解时,该优化问题在任意k时刻都是可行的,则对任意x(k)∈XN和w(k)∈W,闭环系统(19)满足x(k+1)∈XN.由定义3 可知,XN为闭环系统(19)的一个鲁棒不变集.

成立.则联立不等式(26),(32)和(36),由引理1 可知,值函数VN(x(k))为闭环系统(19)的一个ISSLyapunov 函数.因此,闭环系统(19)在XN内相对于扰动具有输入到状态稳定性.□

4 实例仿真

考虑不确定非线性连续搅拌釜反应器(CSTR)

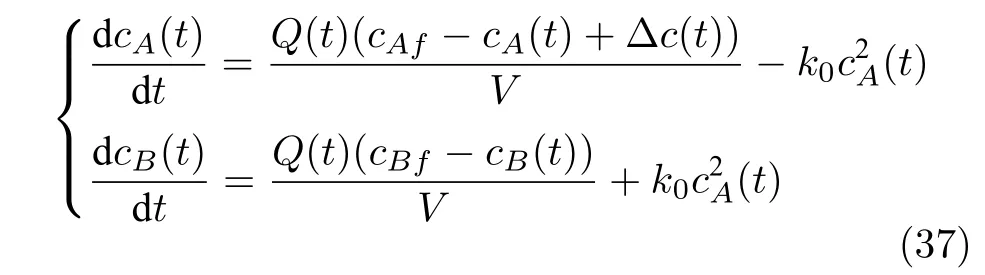
其中,cA和cB分别为组分A和B的浓度,Q为反应器进料流量,cAf和cBf分别为进料中组分A和B的浓度,Δc为进料中组分A 浓度的不确定波动,体积V和反应动力学参数k0.当忽略进料中组分浓度的波动,该模型广泛用于名义稳定EMPC 综合策略的验证[10,13,21].这里假设进料中组分A的浓度波动是有界的,用于验证本文鲁棒EMPC 的有效性.取模型参数[10]:cAf=1.0 mol/l,cBf=0,V=10 l和k0=1.2 l/(mol·min).

令 [cA,cB]T为系统状态[x1,x2]T,Q为控制输入u,w为扰动 Δc.进一步,定义状态约束和控制约束

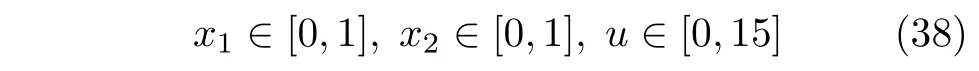
选择采样周期Ts=0.1 min,利用欧拉差分法离散化连续时间模型(37),得CSTR 非线性离散时间模型

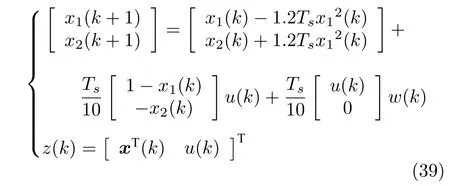
其中,k为采样时刻.定义CSTR 经济性能指标[10]

进一步,为保证终端状态集 Ω 的鲁棒不变性,由式(15)计算容许扰动上界为0.143 6.

令预测步长N=5,仿真总步长Tsim=100,系数λ1=1,并考虑不同收缩因子λ∈[0,1) 的控制效果.选择系统初始状态x0=(0.15,0.7)T,仿真结果如图2和图3 所示,图2 对应持续扰动w(k)=0.1436 sin(k/2)的仿真结果,图3 对应衰减扰动w(k)=0.1436 exp(-k/10) 的仿真结果.分析图2 可知,在持续扰动下,闭环系统最终在最优经济平衡点附近有界稳定;分析图3 可知,在衰减扰动下,闭环状态轨迹渐近收敛于.根据图2和图3 可知,对于不同收缩因子λ∈[0,1),由算法1 得到的鲁棒EMPC 控制器使得闭环系统在相对于容许扰动总是ISS 的,但不同λ对应的闭环状态轨迹的动态响应不同.以衰减扰动w(k)=0.1436 exp(-k/10)为例,由图3 可知,因子λ越小,闭环状态轨迹的收敛过渡时间Ttr越短,具体数据如表1 最右列所示.

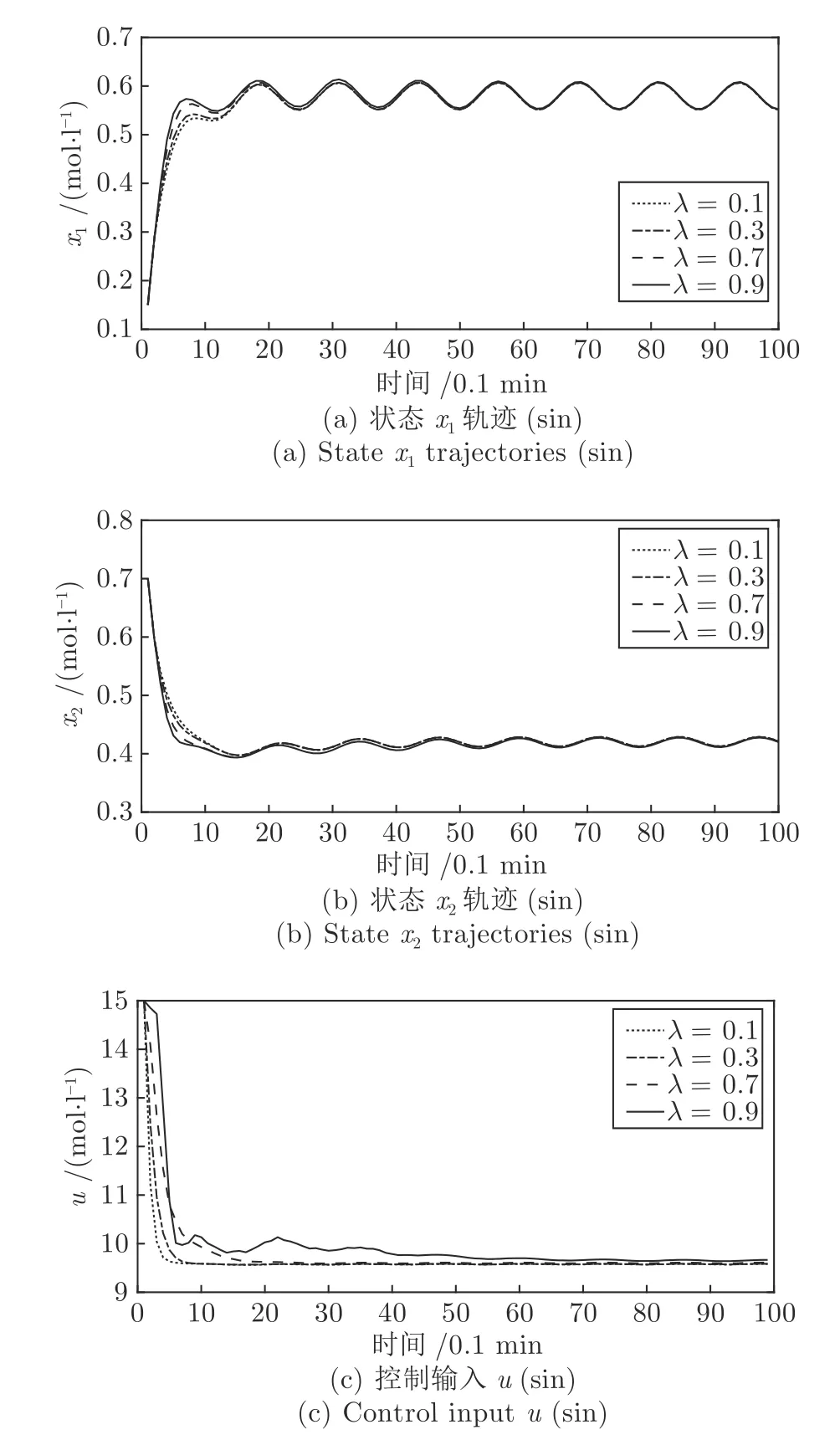
图2 持续扰动 w (k)=0.1436 sin(k/2) 的仿真结果Fig.2 Simulation results under continuous disturbance w(k)=0.1436 sin(k/2)

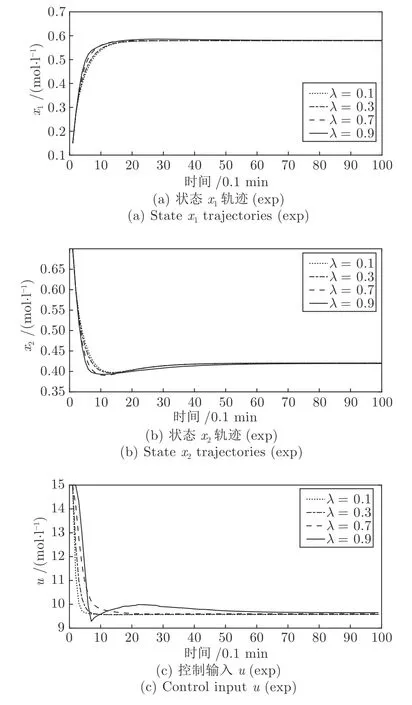
图3 持续扰动 w (k)=0.1436 exp(-k/10) 的仿真结果Fig.3 Simulation results under continuous disturbance w(k)=0.1436 exp(-k/10)

定义闭环系统T步平均经济性能指标

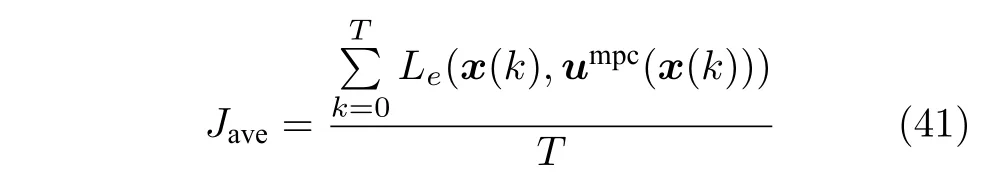
取T=100,表1 给出了不同λ值对应的闭环系统平均经济性能.分析表1 可以看出,因子λ越大,闭环系统平均经济性能越好.这表明,无论是名义系统还是不确定系统,闭环系统的经济最优性和稳定性是互相冲突的双控制目标[10,21].在本文鲁棒EMPC 策略中,可以通过调节收缩因子λ对经济性控制目标和鲁棒稳定性控制目标进行权衡,从而实现经济性和鲁棒稳定性综合控制效果.

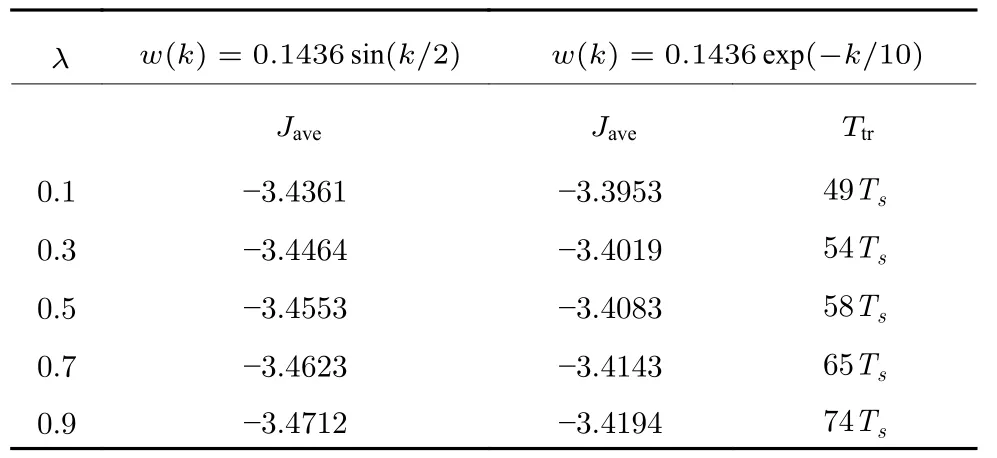
表1 平均经济性能和收敛过渡时间Table 1 Average economic performance and transient time

进一步,为了验证本文鲁棒EMPC 策略(简记为MM-EMPC)的优越性,对比文献[38]中鲁棒收缩EMPC 策略(简记为RC-EMPC),研究不同容许扰动上界对系统稳定性的影响.对约束CSTR 系统(37)和(38),在系统参数相同情况下,RC-EMPC 策略容许扰动上界d1=0.0136,MM-EMPC 容许扰动上界d2=0.1436.选择持续扰动w(k)=0.04sin(k/5),令初始状态x0=(0.5,0.5)T,仿真步长Tsim=500.在相同仿真环境下,两种鲁棒EMPC 策略的控制结果如图4 所示,其中,实线表示MM-EMPC 策略仿真结果,虚线表示RC-EMPC 策略仿真结果.

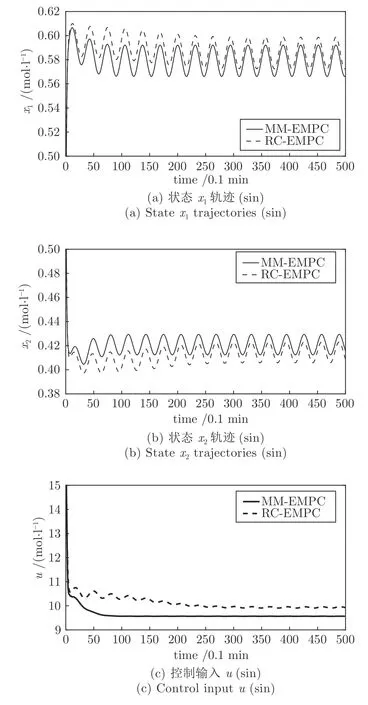
图4 闭环状态轨迹和控制输入曲线Fig.4 Closed-loop state trajectorand control input profiles

从图4 可以看出,MM-EMPC 策略对应的闭环状态轨迹和控制输入曲线均收敛于附近,而RC-EMPC 策略对应的闭环轨迹虽然收敛,但存在较大的稳态误差,且MM-EMPC 闭环系统的动态响应更加快速.进一步,考虑衰减扰动w(k)=0.04 exp(-k/5),选择4 个不同的初始状态对两种控制策略进行仿真对比分析,控制结果如图5 所示.综合图4和图5 分析可知,当容许扰动上界d ∈(d1,d2) 时,MM-EMPC 策略下的闭环系统相对于扰动是ISS 的,而RC-EMPC 却无法保证闭环系统相对于扰动具有ISS,其中一个重要原因是RCEMPC 对大扰动会丢失递推可行性.因此,相较于RC-EMPC 策略,本文策略在保证闭环系统ISS 同时,能够获得更大的容许扰动上界,从而降低鲁棒EMPC 控制器的保守性.

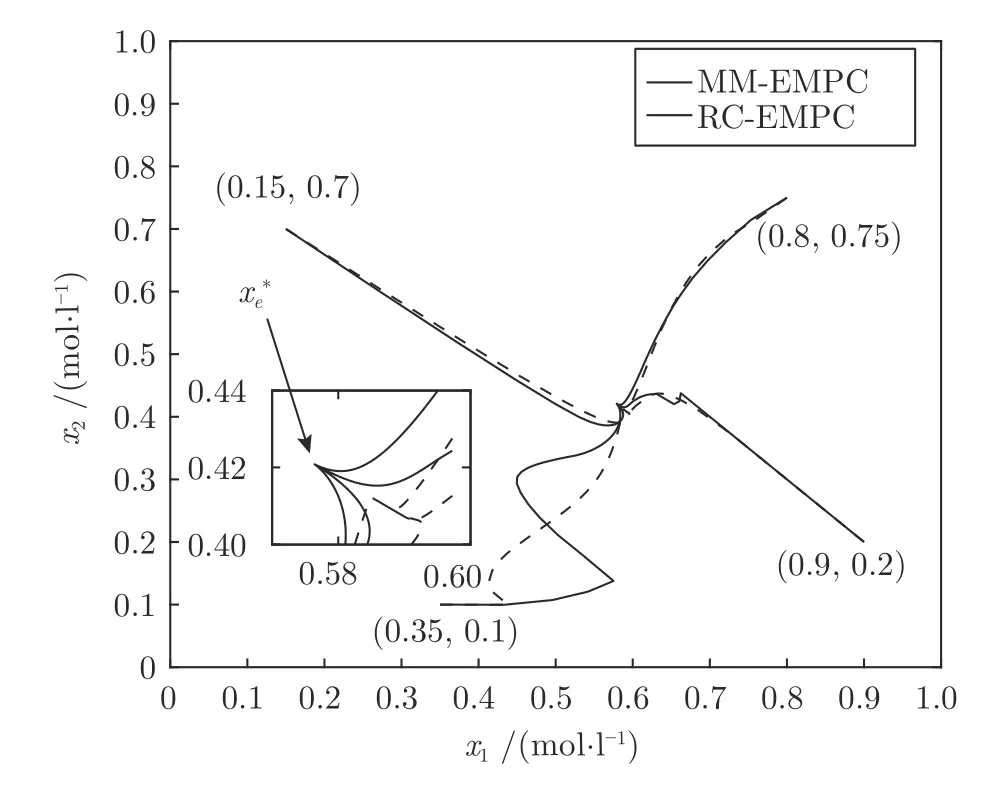
图5 不同初始状态的闭环系统相轨迹Fig.5 Phase trajectories of the closed-loop system from different initial states

5 结束语

本文针对有界扰动下的约束不确定仿射输入非线性系统,提出了一种新的鲁棒EMPC 策略.基于微分对策原理分别对经济目标函数和关于最优经济平衡点的鲁棒稳定性目标函数进行优化,利用得到的鲁棒稳定性目标最优值函数构造隐式收缩约束,保证了双控制目标优化问题的递推可行性,并建立了闭环系统在最优经济平衡点处相对于扰动的输入到状态稳定性结果.通过对不确定CSTR 经济优化控制的对比仿真实验,验证了本文策略的有效性和优越性.

尽管基于微分对策的min-max 鲁棒EMPC 在理论上能有效提高鲁棒EMPC 的性能,但minmax 优化在线计算复杂,将阻碍鲁棒EMPC 在快速响应系统中的应用.因此,降低min-max 鲁棒EMPC 的在线优化计算量和设计更高效的鲁棒EMPC 策略(如Tube 鲁棒EMPC、本质鲁棒EMPC 等)将是后续研究重点.