微电网的电流均衡/电压恢复自适应动态规划策略研究

王 睿 孙秋野 张化光

符号说明

2015 年,巴黎气候变化峰会提出将全球气候变化控制在2 摄氏度之内[1],中、美、欧、日等世界主要国家以此制定了相关的碳达峰和碳中和的目标[2].为实现上述目标,高比例可再生能源成为了最优选择,其中风能和光能被评为最具潜力的两种可再生能源[1,3-4].同时,风能和光能在时间和空间上具有很强的互补特性,例如在我国东北地区气候往往呈现晴天光照充沛而阴天风速较高的特性[5].如何利用此互补特性实现可再生能源高比例消纳成为了当前亟待解决的重/难点问题.如果每个能源主体按照自身容量比例输出其电流,可再生能源的利用率和系统的稳定性/弹性可以得到极大的提升[6].因此,本文提出了基于分布式自适应动态规划的含多类型分布式电源的微电网电流均衡/电压恢复协调控制策略,有助于实现可再生能源的高比例消纳.

近年的研究表明,同时含风能和光能的微电网系统已经得到了广泛的研究并且在各国建立了相关的应用园区,如澳大利亚,德国等[7-8].目前对于此类微电网系统的研究多集中在系统规划设计和最优经济调度而非能源主体的实时控制[9].文献[10]构建了内嵌电源和负载随机变化的典型微电网系统的优化配置策略.文献[11]提出了基于Lp技术的混合规划优化算法以获取最优的微电网系统的配置策略.同时,文献[12]提出了微电网系统分层分布式模型预测控制策略,利用上层分布式迭代控制器实现经济最优,利用底层监督预测控制器以确保跟踪性能.然而,上述研究内容皆未解决微电网系统的实时电流均衡和电压恢复问题.由于含风能和光能的微电网系统广泛存在并且风/光波动下秒级的实时电流均衡尚属空白,因此实时电流均衡控制策略亟待提出.

众多学者常基于不同类型的可再生能源等效为理想直流电压源并且忽略其拓扑异构特性的假设,来研究电流均衡和电压恢复问题或者将风力发电机类可再生能源输出的交流电进行脉冲宽度调制(Pulse width modulation,PWM)整流而获得直流电,此时含风能和光能的微电网源侧都为理想直流源.然而上述的解决方案势必导致风力发电机组类可再生能源多级联一级Boost 变换器,从而导致微电网的建设成本和耗损成本显著增加,随着分布式电源的数量急剧增加,该部分成本势必难以忽略[13].基于理想直流源设定,学者进行了广泛地研究以实现在有/无通信模块下的电流均衡和电压恢复.微电网分级控制策略成为了当前的主流方法.文献[14]从无通信模块控制策略的角度出发,提出了初级下垂控制策略以实现网络的稳定运行.尽管传统的下垂控制器能够较好地实现电力网络的电压调定,但由于线路阻抗差异而致使各个分布式电源间难以实现电流均衡,从而导致可再生能源的利用率降低[15].鉴于此,相关学者提出了内嵌快速通信模块的二级集中控制或主从控制策略以实现各个能源主体间电流均衡和电压恢复[16].然而该类控制策略存在单点故障容忍度低和模型误差敏感等缺陷而难以适用于未来的强分布式电力系统当中[17-18].

针对上述缺陷,相关学者提出了分布式分层控制框架,其中分布式二级协同控制技术被设计以实现电流均衡和电压恢复.其主要可以分为电压-电流曲线幅值调节,电压-电流曲线斜率调节和电压-电流曲线幅值-斜率混合调节三类方法.首先文献[19]提出了电流调节控制器和电压调节控制器以实现电流均衡和电压恢复.进而文献[20-21]提出了分布式电压-电流曲线幅值-斜率混合调节协同控制策略以实现电流均衡和电压恢复.同时即插即用或电压-电流双闭环零级控制策略被嵌入到分层控制框架内以提高系统的可靠性[22-23].而后,针对集群分布式电源的混联系统,文献[24]提出了异构多智能体协同控制策略以实现电流均衡.相似地,文献[25]提出了内嵌电压-电流双闭环的分布式二级控制策略以确保电流均衡和电压恢复.然而上述内容都将不同动态特性的分布式电源简化为理想的直流电压源,其完全忽略了风能和光能的不同电能变换器特性.同时,对电气工程师而言,精准的系统模型是难以获取的.针对系统状态方程模型未知的控制问题,自适应动态规划控制策略提供了很好的选择[26].同时,自适应动态规划策略已经被广泛地应用于实际系统,如智能家居系统和储能系统的能量调度等[27-29].

由于每个能源主体按照自身容量比例输出电流被认为可以有效提高可再生能源的利用率和系统的稳定性/弹性,基于此,本文提出了一种基于广义风光拓扑同胚系统的分布式自适应动态规划控制策略以确保电流均衡和电压恢复.本文的主要特点和优点如下:

1)构建了包含风光实时互补特性的广义风光拓扑同胚系统模型.该模型能够有效简化后续初级和二级控制器设计难度和提供模型基础;

2)将电流均衡和电压恢复问题转化为最优控制问题.基于此,每个能源主体的目标函数被转化为获取最优控制器和最小电压/电流控制偏差;

3)提出了基于贝尔曼准则的自适应动态规划控制策略以实现电流均衡和电压恢复,助力可再生能源的高比例消纳和系统稳定性.同时提出的自适应动态规划策略的收敛性和稳定性被有效证明.

1 电能变换器广义拓扑同胚模型

本部分将构建电能变换器的广义拓扑同胚模型.首先,典型的含风能和光能的微电网系统拓扑结构如图1 所示.其中Wi表征第i个风力发电装置,N表征风力发电装置的数量;Sj表征第j个光伏发电装置,M表征光伏发电装置的数量.风力发电装置和直流母线间的电能变换器为如图2 所示的三相整流器,而光伏发电装置和直流母线间的电能变换器为如图3 所示的升压变换器,显然风机电能变换器的状态方程不同于光伏电能变换器的状态方程.因此,通过严格的数学推导而构建风机/光伏的统一广义电能变换器状态方程显得十分必要.基于此,本文将风机电能变换器转换为等效的光伏电能变换器.

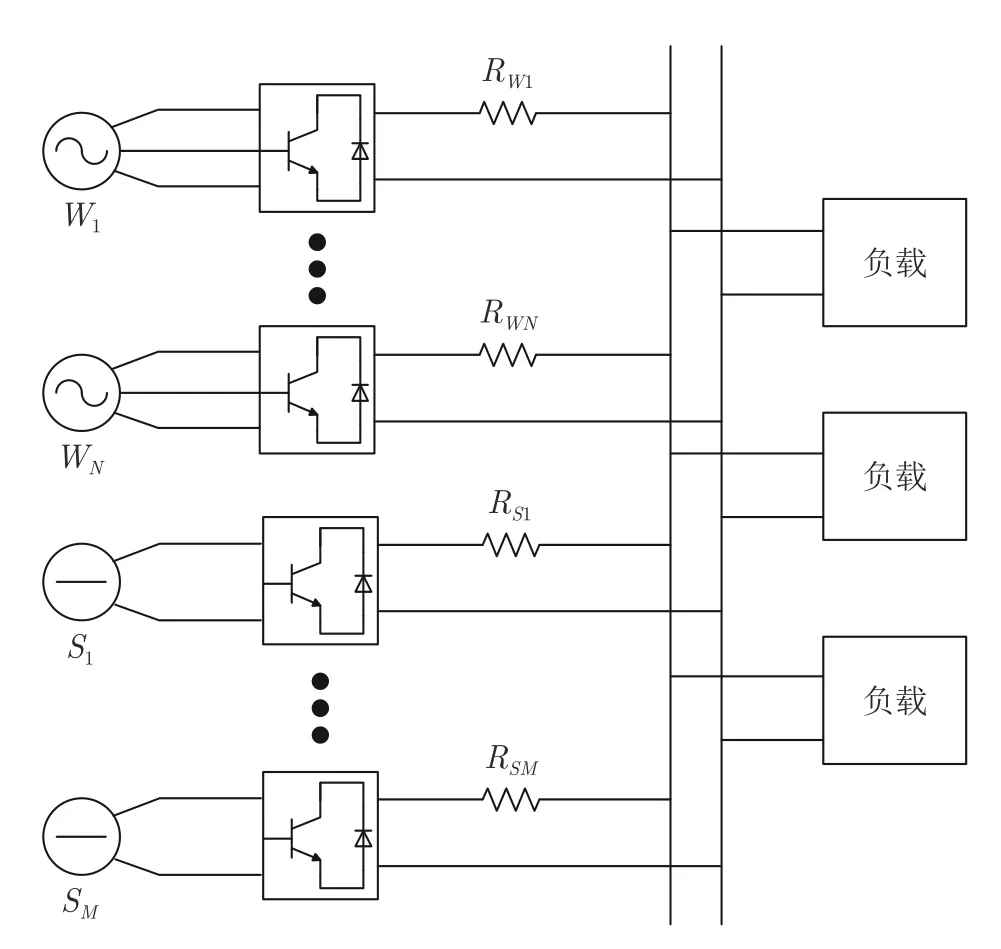
图1 微电网系统拓扑图Fig.1 The typical circuit of the microgrid system

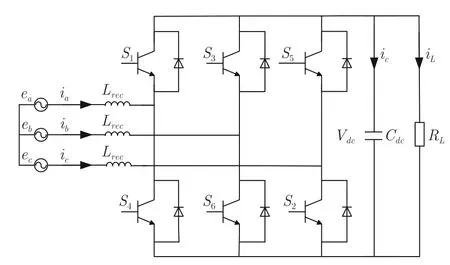
图2 风力发电装置和直流母线间的电能变换器Fig.2 The interface converter between wind energy generator and DC bus

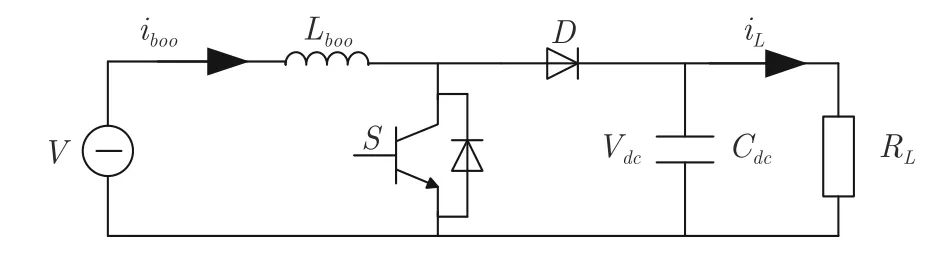
图3 光伏发电装置和直流母线间的电能变换器Fig.3 The interface converter between solar energy generator and DC bus

首先,风机整流型电能变换器的详尽控制器可以通过文献[30]获得,其中风机整流型电能变换器在d-q坐标系下控制.根据基尔霍夫电压/电流定律,每个风机电能变换器的输入输出变量间的状态方程如下所示[30]:

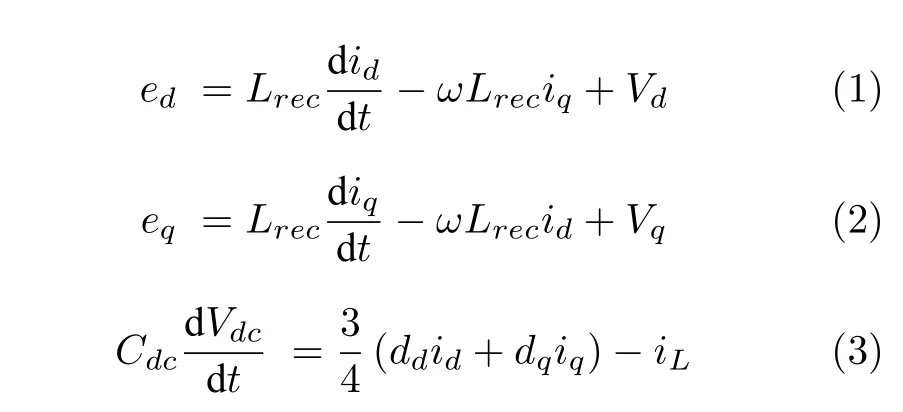
进而风机电能变换器在d-q坐标系下的输入电压Vd和Vq可以重写为如下形式:

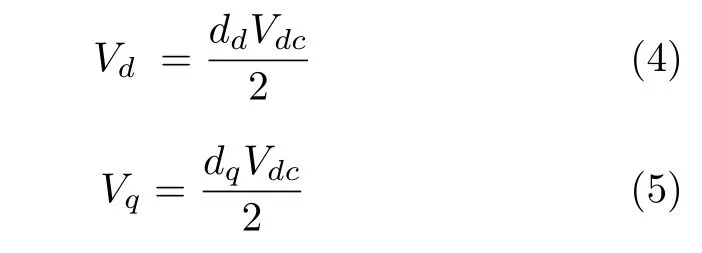
基于式(1)～ (3),电能变换器两侧的功率方程如下所示:

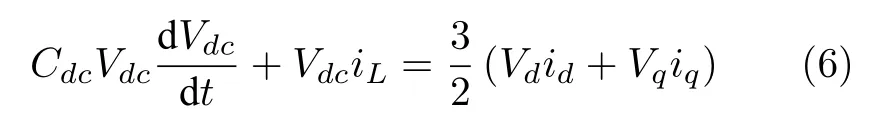
通过式(1)和(2)可知,电压和电流在d-q轴是耦合的,其中耦合项分别为ωLreciq和ωLrecid.进而,风机电能变换器在d-q坐标系下的输入电压Vd和Vq可表达为

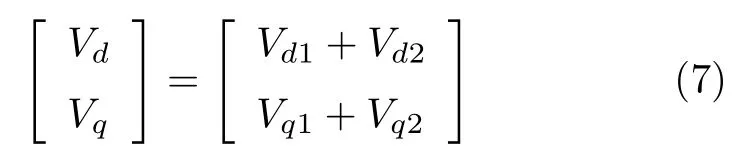
其中,Vd1和Vq1表征耦合部分

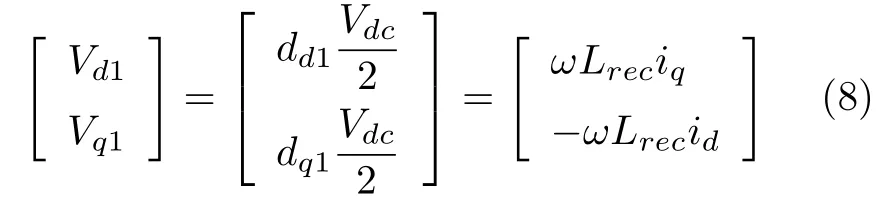
其中,dd1=2ωLreciq/Vdc和dq1=-2ωLrecid/Vdc.因此,式(1)和(2)可以重写为如下:

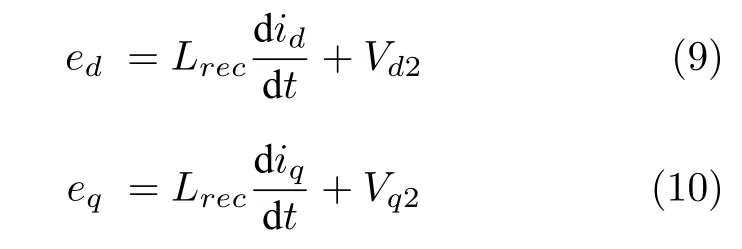
将式(7)和(8)嵌入式(6)

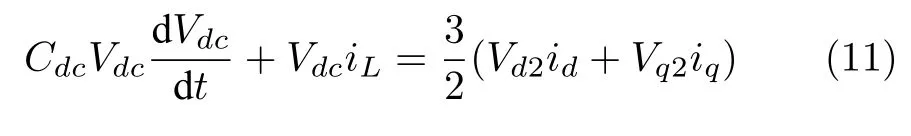
当系统稳定时,eq=0和Vq2=0[18],等式(11)可以简化为

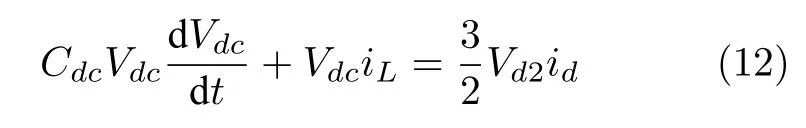
由于q轴电流对d轴的动态特性影响较低而可以忽略[31],因此,电能变换器的系统模型如下所示

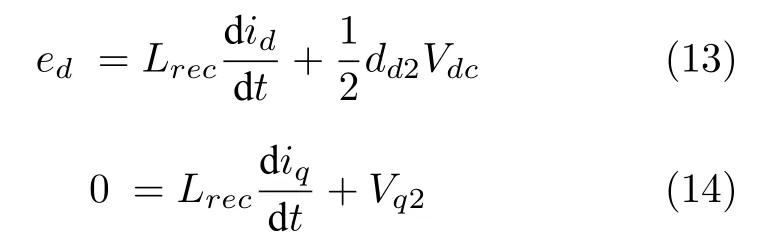
已知,传统的升压变换器的状态方程如下所示:

通过观察传统升压变换器,一个中间变量被引入到风机电能变换器状态方程中,即d=1-dd2,其中d表征等效的占空比,基于式(9)、(10)、(12)、(15)、(16)可知,风机电能变换器的状态方程如下所示:

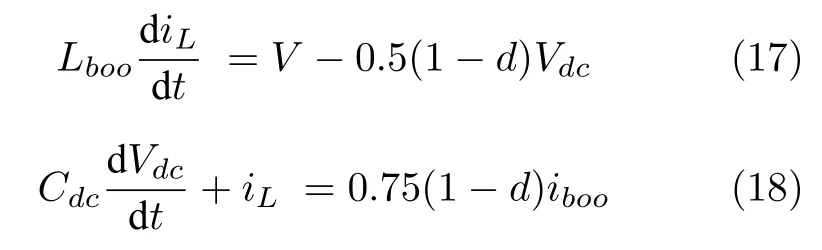
式(17)和(18)说明风机电能变换器的拓扑可以从图2 等效为图4.基于此,风机电能变换器和光伏电能变换器存在拓扑同胚特性,其致使风机电能变换器等效为广义风光拓扑同胚系统.其中,风机电能变换器等效部分的控制器如图5 所示.因此,风机电能变换器可以等效为光伏升压电能变换器.进而含多风机和光伏的微电网系统可以等效为图6所示.可再生能源和直流母线通过广义升压变换器连接.

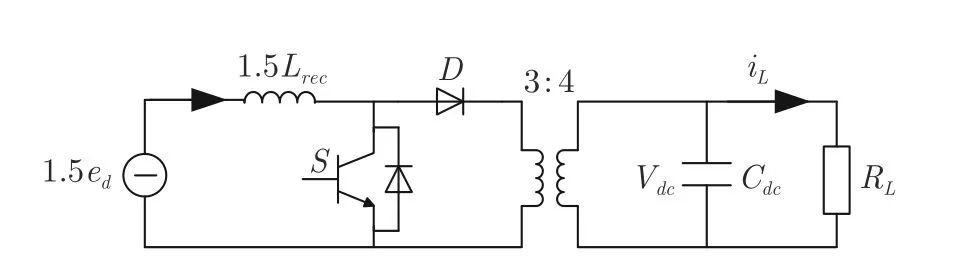
图4 风力发电装置与直流母线的等效电能变换器Fig.4 The equivalent interface converter between wind energy generator and DC bus

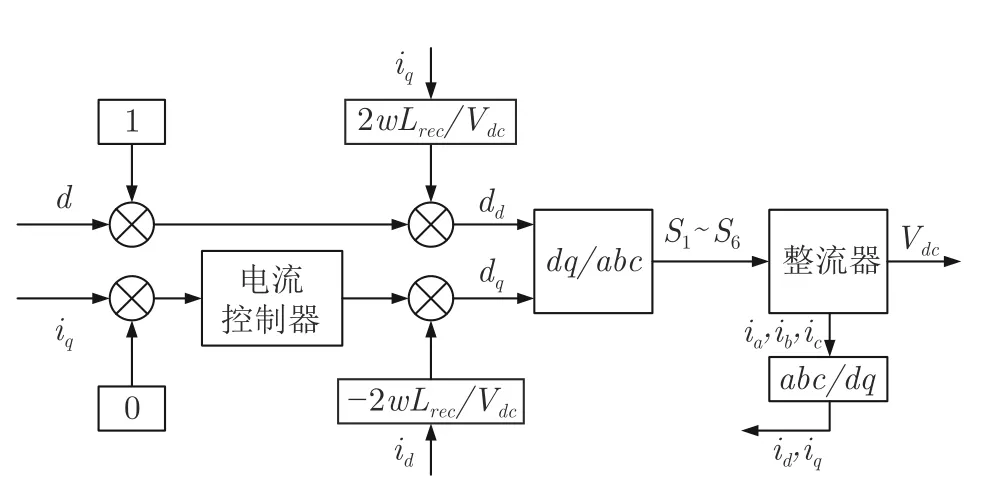
图5 风力发电装置等效拓扑同胚电能变换器控制框图Fig.5 Control block diagram for realizing the equivalent topological homeomorphism system of the wind energy interface converter

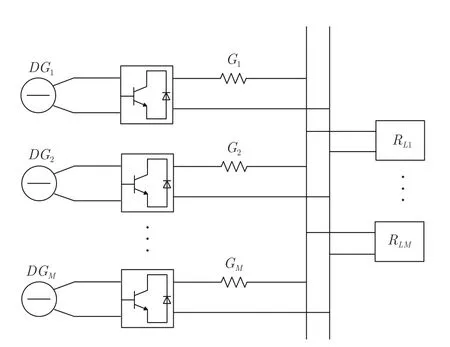
图6 基于广义升压变换器的微电网系统Fig.6 The typical circuit of the microgrid system based on generalized boost converter

注 1.本节建立电能变换器模型是为了有效降低后续控制器设计的难度,基于数学推导可知风机电能变换器和光伏电能变换器存在相似的状态方程,从而可以将原本不同类型电能变换器设计不同控制策略的问题简化为设计一套统一控制策略的问题,从而大幅度降低了后续两级式控制器设计的难度,即降低了初级电压-电流双闭环控制器参数选取的难度和二级自适应动态规划控制器神经网络训练的难度.同时相关的统一建模结果可以为其他先进控制策略提供模型基础.

2 电流均衡和电压恢复

对于图6 所示的含多风机-光伏型可再生能源的微电网系统,定义US={1,2,···,N}和UL={1,2,···,M}.分布式电源通过广义升压变换器连接至直流母线,其电压为VDC.第i个广义升压变换器的输出电压和电流为Vi和ii,i∈US.通信网络模型被描述为一个带有节点US,边H∈US×US和邻居连接矩阵A=(aij)N×N的拓扑图Ω=(US,H,A) .其 中aij＞0 当且仅 当DGi可以从DGj获取信息,反之则,aij=0 .如果i/=j,拓扑图Ω 拉普拉斯矩阵L=(lij)N×N定义为lij=-aij.否则,lij=.定义 Ψi为包含邻居节点i的集合.毫无疑问,如果两个节点间存在通路,则信息流可以被定义为连接.本文的主要目标是实现电流均衡和电压恢复,其实现的充要条件如下所示

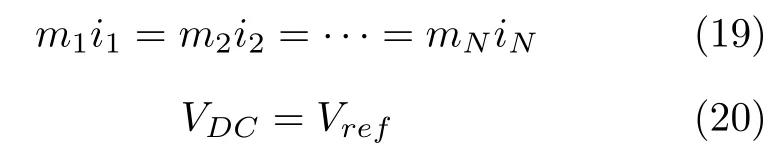
其中mi反比例于该可再生能源的实时额定电流.为了实现上述电流均衡和电压恢复的目标,分层控制策略被广泛应用[32].在此控制策略中,每个分布式电源DGi存在一个本地控制器,其包含内环电压/电流双闭环控制器或即插即用控制器,初级控制器和二级控制器.其中内环电压电流双闭环或即插即用控制器聚焦于广义升压变换器的电压稳定输出以确保广义升压变换器的输出电压可以很好地跟踪电压额定值Vref.在本文中,V/f控制器被应用于初级控制器当中,而二级控制器直接为内环电压/电流双闭环控制器提供电压额定值Vref[33].分布式二级控制被嵌入用来提供辅助补偿项ui,以实现电流均衡和电压恢复.具体的控制器如下所示:

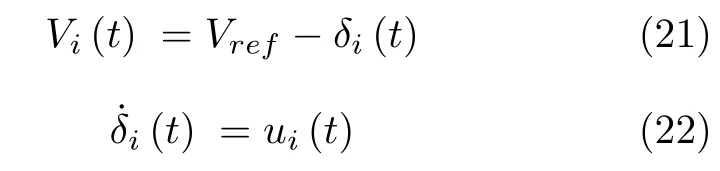
分布式迭代学习策略被应用于二级控制器,对于每个分布式二级控制器,控制模块被当作为智能体.基于此,定义t1,t2,···表征为一个内含时间间隔h的离散序列,其中h表征为h=tk+1-tk.因此式(21)和(22)可以被重新写为:

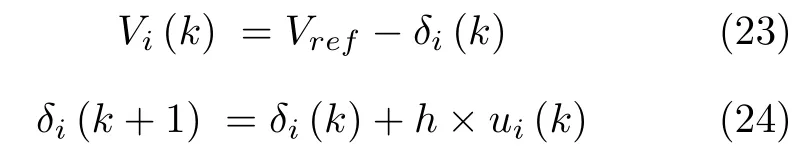
如图6 所示,此微电网系统的功率流可以表征如下:

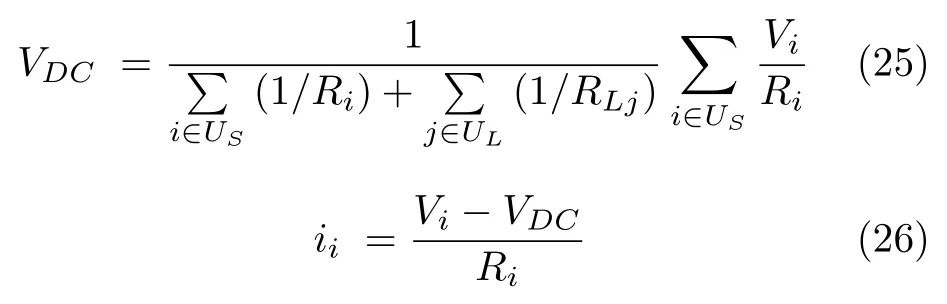
为了实现电流均衡和电压恢复,第i个分布式电源的电流分担偏差和电压恢复偏差分别被定义为EIi(k)和Ev(k) .其可以表征如下:

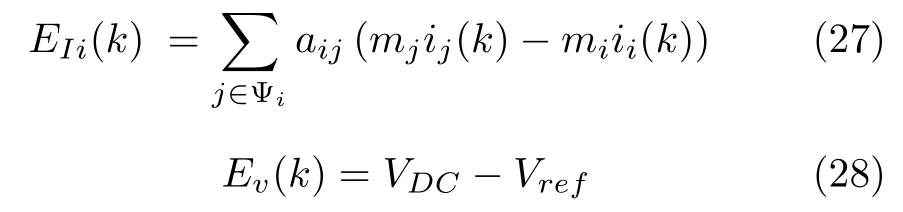
以复合的形式重新撰写,分布式电源的电流分担偏差 可以表征为EI(k)=-LMi(k),其 中M=diag{mi,m2,···,mN}.因此,LM的零空间表征为span{m1,m2,···,mN}当且仅当 Ω 是连接的.基于此,EI(k)=0 等价于对于∀i,j ∈US满足m1i1=m2i2=···=mNiN.毫无疑问,电流均衡和电压恢复可以被实现当且仅当EI(k)=0和EV(k)=0 .基于式(23)～ (28),电流分担偏差和电压恢复偏差的动态可以表征为:

其中,α∈(0,1] .基于此,性能指标函数的动态与性能因子依赖于控制器动作.首先,纳什均衡技术的定义被引入,定义u-i={uj|j ∈US,j/=i}作为除第i个智能体以外的智能体控制器动作.基于此,期望的电流均衡和电压恢复控制器ui(k) 应该被提供以确保N个智能体达到纳什均衡,为了更好地说明相关情况,两个定义被提供如下:

定义 1.如果控制动作ui(k) 可以保证式(29)和(30)稳定且Pi是有限的,则控制动作ui(k) 是最优控制动作.

定义 2.对于含有N个最优控制决策元组(())的N个主体的动态博弈系统应该存在一个纳什均衡解,如果对于所有的i ∈N

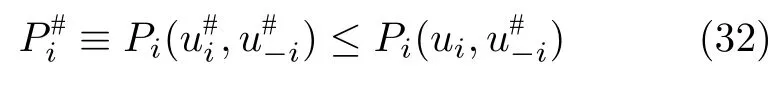
其中N个元组被定义为N个主体的纳什均衡结果.

根据上述的定义,期望的电流均衡和电压恢复控制动作ui(k) 不仅可以保证电流均衡和电压恢复,还可以保证微电网系统达到纳什均衡解.

3 基于贝尔曼准则的自适应动态规划技术

在本节中,最佳的控制器ui(k) 利用基于贝尔曼准则的自适应动态规划技术获得.首先,贝尔曼函数定义如下:对于某控制动作ui(k),∀i ∈US,其值函数为

式(38)所提供的控制动作可以确保微电网系统达到纳什均衡/渐近稳定,同时实现电流均衡和电压恢复,具体原因如定理1 所示:

定理1.选取最优值函数满足式(34),控制器可以同时满足下述两个条件:1)电流均衡和电压恢复可以得到满足;2)微电网系统能够达到纳什均衡,即系统渐近稳定.

证明.定义每个分布式电源的李雅普诺夫方程为:

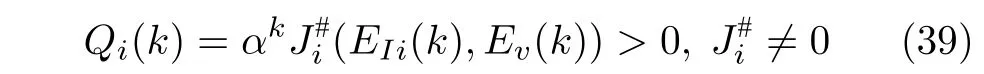
然而,式(36)是一个HJB 方程,其难以获取解析解.而基于贝尔曼准则的自适应动态规划技术可以有效获取该HJB 方程的数值解[34].基于此,本文选用基于贝尔曼准则的自适应动态规划技术获得最佳控制器.

根据文献[6,26-28]和[34],自适应动态规划可以被分为以下四步:

4 执行网-评价网神经网络

本文采用执行网-评价网的结构实现值迭代策略以实现精准的电流分担和电压恢复协同控制.如图7 所示,为了能够迭代逼近最优解和,利用神经网络来得到控制动作ui(k)和值函数Ji(k) .具体实现结构及方式如下.

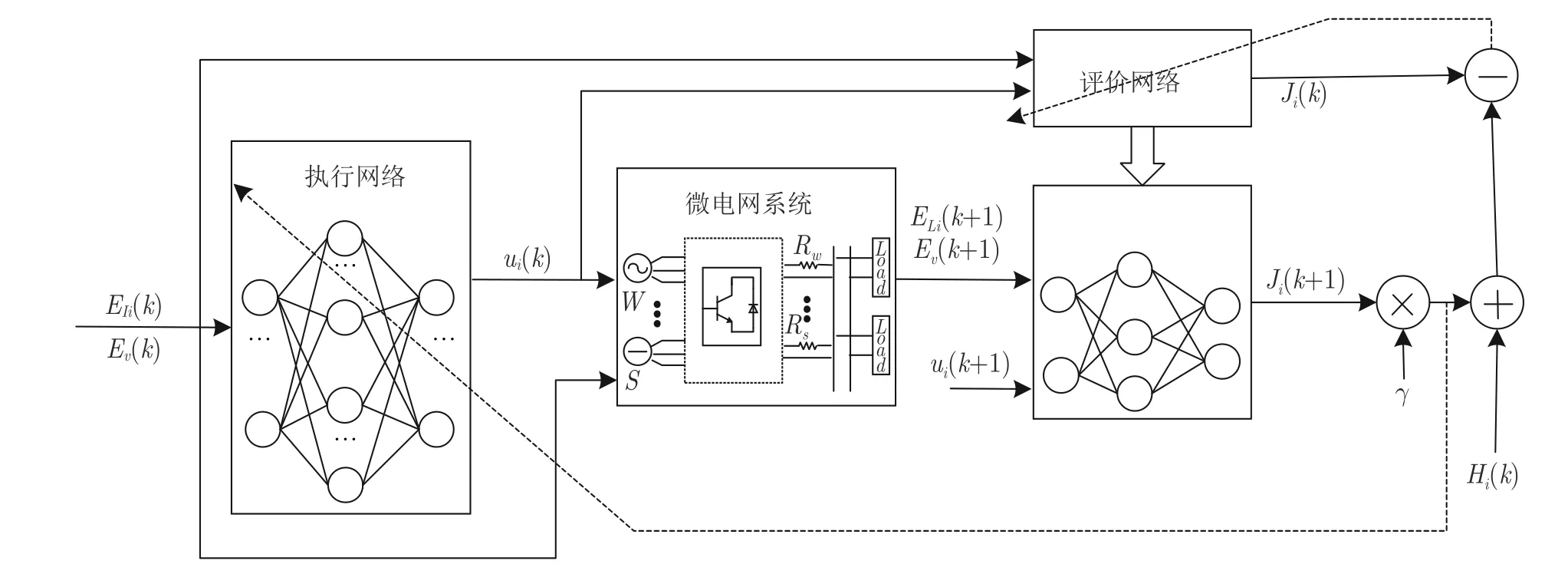
图7 自适应动态规划结构Fig.7 The adaptive dynamic programming structure

4.1 评价网络

评价网络由三层BP 神经网络得到值函数Ji(k),其输入由维向量xi(k)=[EIi(k),EV(k)]T和维向量ui(k) 构成.设隐含层有Nc个神经元,输入层到隐含层的权重参数为,隐含层到输出层的权重参数为,于是评价网络的输出为

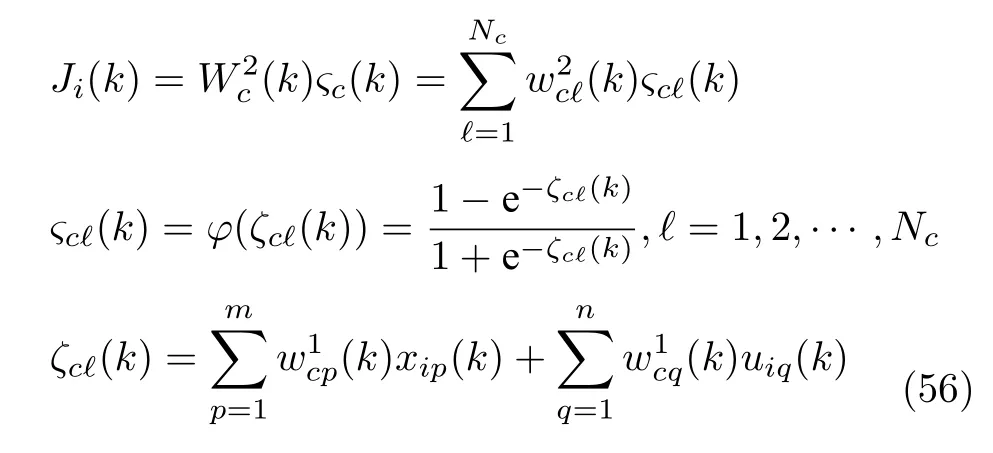
4.2 执行网络

与评价网络一致,执行网络结构同样由三层BP 神经网络构成,其输入和输出分别为xi(k)和ui(k) .设其隐含层由Na个神经元构成,并且输入层到隐含层的权重参数为,隐含层到输出层的权重参数为,则执行网络的输出方程表达为

注 2.本文所提出的相关建模方法和控制器设计方法可以推广至混联可再生能源系统中.即风/光异构的分布式电源可以利用本文第1 节的内容进行统一建模,进而利用现有文献[35]获得混联系统的功率流动方程以替换本文的式(25)和(26).后续的相关控制器的设计和稳定性/收敛性的证明不变,这也体现了本文方法的通用性.本文模型未知部分在于系统状态方程未知,其中包括由于隐私保护等原因造成的初级和零级控制器具体参数未知.值得注意的是,本文第一部分仅将风机电能变换器转换为等效的光伏电能变换器,从而可以将原本不同类型电能变换器设计不同控制策略的问题简化为设计一套统一控制策略的问题,从而大幅度降低了后续两级式控制器设计的难度.然而本文并未建立包含初级和零级控制器的精准状态方程,而是通过输入/输出数据训练神经网络得到基于自适应动态规划策略的微电网二级控制器.

5 仿真分析

在本部分,本文提出的自适应动态规划控制策略将利用Matlab/Simulink 测试系统验证,本测试系统包含两个风力发电装置和两个光伏发电装置,负载总耗能为192 W,直流母线电压参考值为48 V.每个分布式电源通过广义升压变换器接入直流母线.详细的控制参数如下所示:分布式电源与直流母线间的线路阻抗分别为R1=0.15 Ω,R2=0.2 Ω,R3=0.25 Ω和R4=0.3 Ω .全部广义升压变换器的电感和电容分别为 300 μH和1 500 μH.全部广义升压变换器的输入电压为12 V.全部广义升压变换器的内环电压/电流双闭环PI 参数分别为 (1.2+120)s和(0.8+10)s .对于二级控制器,采样时长为h=0.01 s ;折扣因子为α=0.97,学习率lc和la为0.05,隐含层神经元个数Nc=Na=5 ;正值权重a=b=1和c=0.15 .

5.1 电流均衡/电压恢复效果验证

为了更好地验证提出的自适应动态规划控制策略对于电流均衡和电压恢复效果的有效性,此测试系统的时间序列选取为 [0,9] s .其中,在初始时刻,提出的自适应动态规划控制策略未被采纳,同时四个分布式电源的额定电流比为1:1:1:1,在t=1 s 时刻,提出的自适应动态规划控制策略嵌入至二级控制器当中.进而在t=5 s 时刻,由于气象因素改变,风力发电装置的实时额定电流增加而光伏发电装置的实时额定电流降低,两者的实时额定电流比为3:2.基于此,自适应动态规划控制策略对于电流均衡和电压恢复效果的有效性可以得到验证当且仅当在t=[1,5] s 时,广义升压变换器的输出电流比为1:1:1:1,而在t=[5,9] s 时,广义升压变换器的输出电流比为3:3:2:2.同时在t=[1,9]s 内,直流母线电压稳定在48 V.如图8 所示,广义升压变换器的实际输出电流比为1:1:1:1,而在t=[5,9]s 时,而广义升压变换器的实际输出电流比为3:3:2:2.因此电流精准分担任务可以被很好地实现,每个广义升压变换器的实际输出电压如图9 所示.同时,直流母线的实时电压如图10 所示,由此可知,在t=[1,9]s内,直流母线的实时电压持续稳定在48 V.此过程中系统的值函数和控制输入随着迭代次数的收敛曲线分别如图11和12 所示,其可以在2 s 之内收敛至0.综上所述,本文提出的自适应动态规划控制策略具有良好的性能.

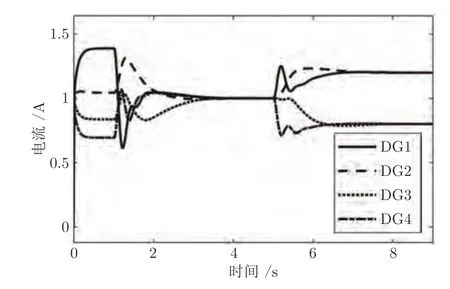
图8 微电网系统实时电流Fig.8 Real-time current of distributed generators in the microgrid system

图9 微电网系统分布式电源实时电压Fig.9 Real-time voltage of distributed generators in the microgrid system

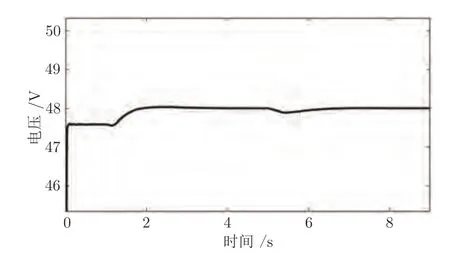
图10 微电网系统直流母线实时电压Fig.10 Real-time voltage of DC bus in the microgrid system

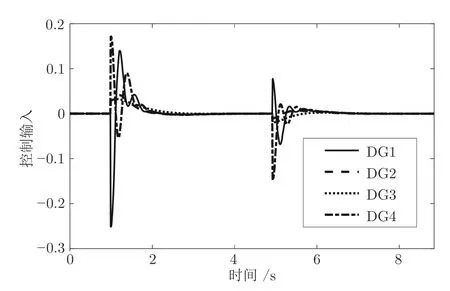
图11 控制输入曲线Fig.11 Control input curves

5.2 仿真对比效果验证

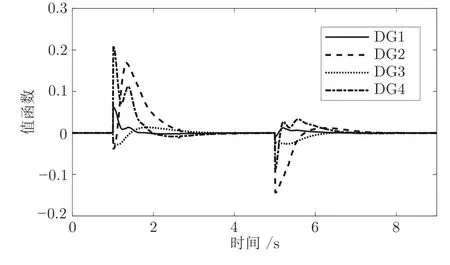
图12 值函数曲线Fig.12 Value function curve

本文的核心创新在于风/光协同调度的微电网多关注分钟级的调度或优化问题而非风/光波动下秒级的实时电流按容量比例精准分担,简称电流均衡,而精准电流均衡有助于可再生能源的高比例消纳.为了实现含风/光等拓扑异构的可再生能源系统的电流均衡和电压恢复策略,本文提出了自适应动态规划策略.不可否认,在传统理想直流源假设下,电流均衡和电压恢复已经被广泛地研究,其中二级控制器采用多智能体的方法已经成为主流,如文献[16,18,24-25,32].基于此,本文从微电网的实际电流均衡效果出发,与采用多智能体控制方法的文献进行对比.本文选取与文献[24]中的基于多异构智能体的H-无穷控制策略相对比.选取4 个分布式电源的额定电流比为1:1:1:1.实际的电流控制效果如图13和14 所示,其中图13 表征基于文献[24]的微电网系统实时电流均衡情况和图14 表征基于本文提出的电流均衡/电压恢复控制策略的微电网系统实时电流均衡情况.虽然基于文献[24]的控制方法和基于本文提出的电流均衡/电压恢复控制方法都可以实现精准的电流均衡,然而基于文献[24]的控制方法的电流的最大超调量和反应时间都不如本文提出的控制算法.基于此,本文所提出的电流均衡/电压恢复控制策略具备更好的控制性能.

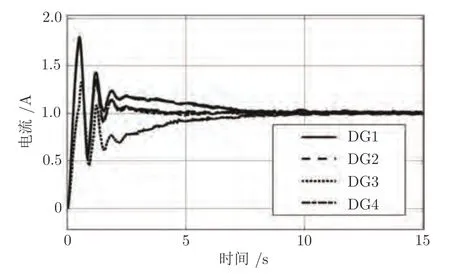
图13 基于文献[24]的微电网系统实时电流Fig.13 Real-time current of distributed generators in the microgrid system based on reference [24]

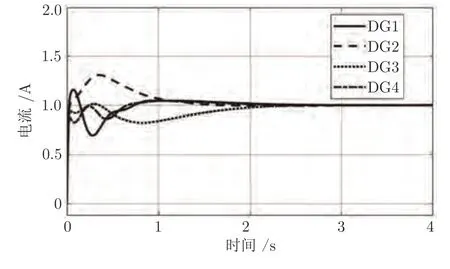
图14 基于本文方法的微电网系统实时电流Fig.14 Real-time current of distributed generators in the microgrid system based on this paper

5.3 结论

随着低碳经济越来越受到各国政府的广泛关注,风能和光能已经成为实现该目标的两大核心手段.虽然同时含风能和光能的微电网系统已经得到了广泛的研究,但其秒级实时电流按容量比例精准分担和电压实时恢复尚未实现.基于此,本文提出了微电网系统中基于自适应动态规划的电流均衡和电压恢复控制策略.相较于现有文献,本文存在以下三个主要优势:1)本文完成了内嵌风光实时互补特性的广义风光拓扑同胚系统模型的构建.其能够有效简化后续控制器设计难度和提供模型基础;2)电流均衡和电压恢复问题已经被转化为最优控制问题.基于此,每个能源主体的目标函数已经被转化为获取最优控制器和最小电压/电流控制偏差;3)基于贝尔曼准则的自适应动态规划控制策略已经被提出,其能够有效确保电流均衡和电压恢复,从而提高了可再生能源的利用率和系统稳定性.与此同时提出的自适应动态规划策略的收敛性已经被证明.最后仿真结果验证了所提自适应动态规划控制策略的有效性.