基于混合变分自编码器回归模型的软测量建模方法

崔琳琳 沈冰冰 葛志强

在实际工业生产过程中,需要对一些关键的质量变量进行实时测量,如产品浓度、过程气体含量、催化剂活性和熔体指数等,这对实现有效的过程控制和提高产品质量具有重要意义[1-5].然而,由于极端的测量环境、昂贵的仪器成本、大的分析测量延迟等因素,关键质量变量的物理测量难以实现[6-8].因此,软测量技术应运而生.软测量是一种虚拟传感器技术,通过构建数学模型,以一组容易测量的相关过程变量为输入,以过程关键质量变量为输出,来快速准确地估计这些难以直接测量的质量变量[9-11].一般来说,软测量方法可大致分为两种,模型驱动的软测量和数据驱动的软测量[12-13].与前者相比,数据驱动的软测量方法不需要精准的机理模型和大量的过程专家知识,更加具有灵活性和实用性.此外,随着分布式控制系统(Distributed control systems,DCSs)在现代工业过程中的广泛使用,收集到的数据也日益增多,为数据驱动建模方法提供了丰富的数据保证[14].因此,数据驱动的软测量方法受到了越来越多的关注.经典的基于数据驱动的软测量建模方法有主成分回归分析(Principal component regression,PCR)[15]、偏最小二乘法(Partial least squares,PLS)[16]、支持向量机(Support vector machine,SVM)[17]和人工神经网络(Artificial neuralnetwork techniques,ANN)[18]等.

近年来,深度学习作为一种新兴技术,在图像处理、计算机视觉、自然语言处理等应用领域都取得了很大的进展.与传统的浅层方法相比,深度学习方法具有更深的网络结构,它能够通过多层非线性映射,从数据中提取更深层的抽象特征,具有强大的数据建模能力.因此,面对越来越复杂的大规模现代工业过程,深度学习具有不可替代的优势,已经被应用到了软测量领域当中[19].例如,Yao和Ge 提出了一种基于分层极限学习机的半监督深度学习软测量模型[20].Yuan 等开发出一种质量相关自动编码器,用于提取深层次的输出相关特征[21].Zhang和Ge 基于门控循环单元和编码解码网络,设计了一种深度可迁移动态特征提取器,并应用于软测量[22].Zheng 等将集成策略、深度信念网络和核学习集成到软测量框架中,建立了集成深度核回归模型,并扩展到半监督形式[23].然而,由于过程的随机扰动等原因,几乎所有的过程数据都会受到随机噪声的污染,从本质上来说,过程变量都属于随机变量[14,24-25].最近,Kingma和Welling 提出了变分自编码器[26],一种深度生成模型,它结合了深度学习和贝叶斯变分推断.作为一种以深层神经网络为结构的概率框架模型,VAE 既具有深度学习的非线性特征提取能力,又能像概率模型那样对过程不确定性和数据噪声进行建模.基于这些优点,VAE已经被引入到工业过程中,并逐渐被用于过程监测和软测量建模等应用场景[27-31].

尽管目前VAE 在软测量应用中取得了一些进展,但是传统的VAE 通常假设其潜在变量分布服从高斯分布,因此模型学习到的特征表示只能是单峰形式,难以充分发挥潜在空间编码的能力和灵活性.这在很大程度上限制了VAE 对复杂特性过程数据的描述,如工业领域广泛存在的多模态数据,VAE 的建模性能很难得到有效的保障.在实际工业过程中,由于原料比例、产品需求、制造策略等因素的变化,经常会发生操作条件的转变,即工况发生变化,从而使过程数据呈现典型的多模态特性[32-34].近年来,学者们提出了一些VAE 变体模型,通过使用复杂的先验等手段来促进编码的灵活性,但他们的目标大多是进行无监督聚类[35-37].到目前为止,还没有VAE 在多模态工业过程软测量应用中的相关研究报导.基于以上讨论,本文结合高斯混合模型的思想,基于VAE 框架提出一种混合变分自编码器回归(MVAER)模型,用于解决多模态过程的质量预测问题.该方法采用高斯混合模型来描述VAE 的潜在空间变量分布,分别对应工业过程中的多个模态.通过非线性映射将复杂多模态数据映射到潜在空间,学习各模态下的潜在变量,获取原始数据的有效特征表示.同时,建立潜在特征表示与关键质量变量之间的回归模型,实现软测量应用.通过一个数值算例和一个实际工业案例,验证了所提方法的有效性和可行性.

本文的其余部分组织如下.在第1 节中,简要回顾了VAE 模型.在第2 节中,介绍了所提出的MVAER 模型的主要思想和详细的推导过程,并介绍了基于MVAER 的软测量建模与应用方法.在第3 节中,通过两个案例对MVAER 进行了性能评估.最后,在第4 节中得出本论文的结论.

1 VAE 概述

VAE 是一种无监督的深度生成模型,结合了深度学习和贝叶斯概率推断的观点.它假设数据x是由某个具有不可观测的连续随机隐变量z的随机过程产生的.观测数据的边际似然可以写为:

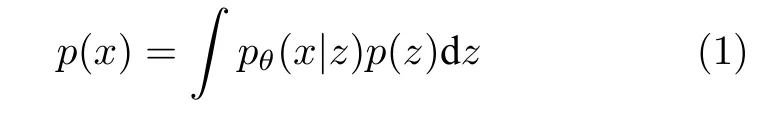
其中,pθ(x|z) 是生成模型,可以被描述为多元高斯分布,p(z) 是先验,通常被简单地设置为标准高斯分布 N (0,1) .

根据贝叶斯定理,可以得到隐变量z的后验分布为.然而,由于生成模型的参数θ和隐变量都是未知的,这里隐变量的积分和后验概率都是难以处理的.因此,VAE 根据变分推断的思想,引入一个额外的变分分布qφ(z|x) 作为推断模型,来近似难解的真实后验.与生成模型相似,推断模型qφ(z|x) 也可以描述为多元高斯分布.

VAE 的优化目标是最大化边际似然函数的证据下界.

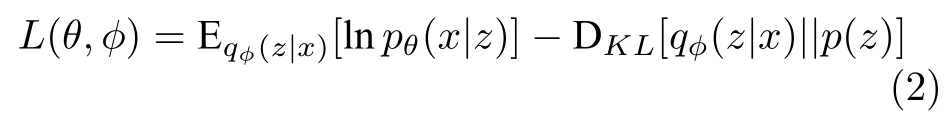
其中,等号右边的第一项是给定pθ(x|z) 时,lnpθ(x|z)的期望,用来保证重建数据与真实数据之间的匹配程度;第二项是一个Kullback-Leibler (KL)散度项,可以被看作是一种正则化,指导近似后验分布尽可能地接近先验分布.

VAE 的模型结构如图1 所示.可以看到,在VAE 中,推断模型qφ(z|x) 被参数化为一个参数为φ的神经网络,称为概率编码器.它将输入数据映射到低维潜在空间,得到其隐变量表示z,这可以看作是对输入数据的特征提取;pθ(x|z) 被参数化为另一个参数为θ的神经网络,称为概率解码器,它从潜在空间中重建原始数据.通过最小化负变分证据下界,同时优化模型的参数φ和θ.更多详细内容可以参考文献[26,38-39].

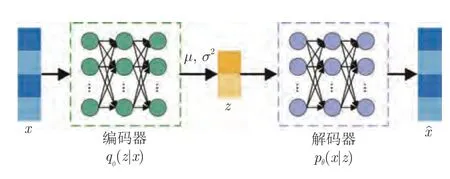
图1 VAE 模型结构图Fig.1 Model structure of VAE

2 基于混合变分自编码器回归模型的软测量方法

在实际应用中,传统的基于VAE 的软测量方法难以对工业中广泛存在的多模态数据进行有效的特征提取.为了解决这一问题,本节将提出一种混合变分自编码器回归模型,并将其应用于软测量模型的构建.总体而言,该方法结合了VAE 框架和高斯混合模型,并将特征提取和回归建模融为一体,使其对复杂多模态过程的关键质量指标数据具有更好的预测性能.

2.1 混合变分自编码器回归模型

混合变分自编码器回归模型本质上是建立在VAE 框架上,同样可以通过生成模型和推断模型来描述.

模型假设输入数据x由随机连续潜在变量z生成,z在潜在空间中服从高斯混合分布.为了建立关键质量变量,即输出变量y的回归模型,假设y也由潜在变量z生成,那么生成过程可以描述为:

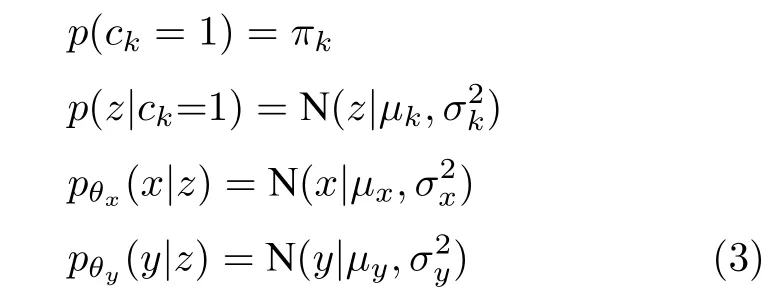
根据上述生成过程,生成模型可以用联合概率分布表示并被分解为:

数据样本点的边缘概率p(x,y) 的 l og 似然函数可以推导为:

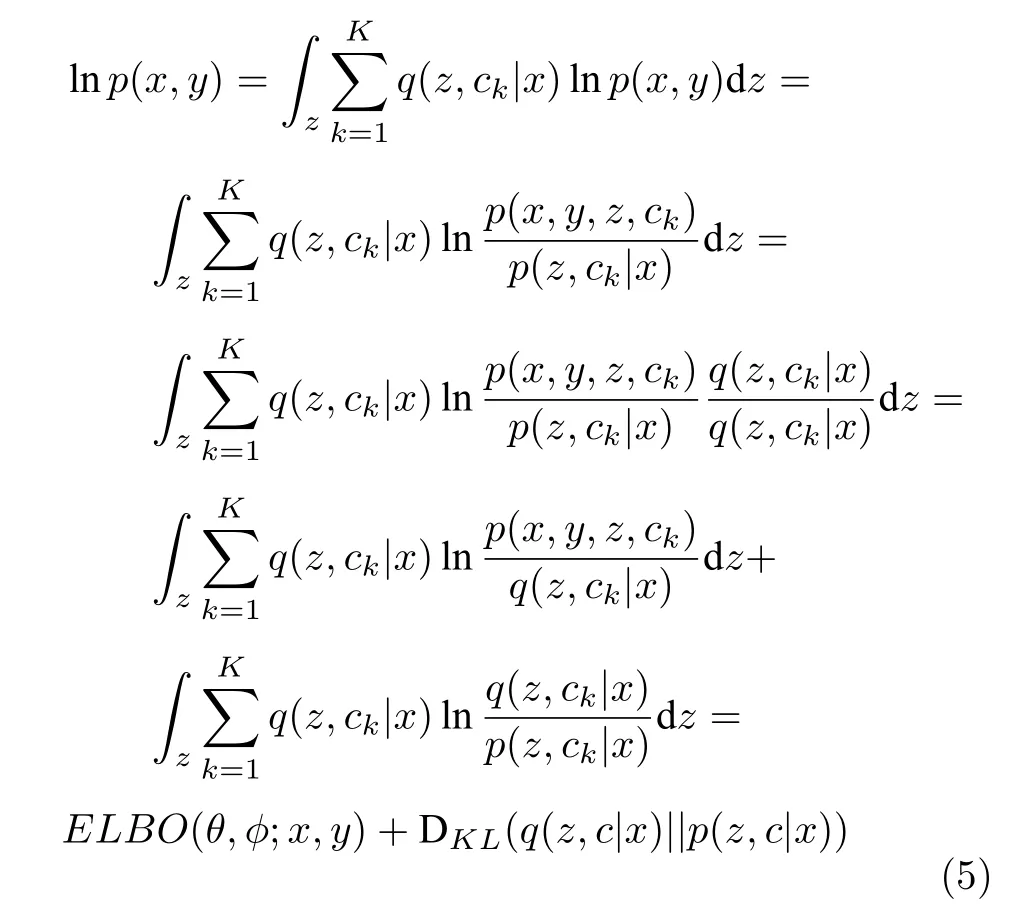
其中,ELBO(θ,φ;x,y) 是边缘概率似然函数的证据下界;qφ(z,c|x) 是推断模型,作为一个额外引入的变分后验,用来逼近难以计算的真实复杂后验p(z,c|x),可以被分解为:

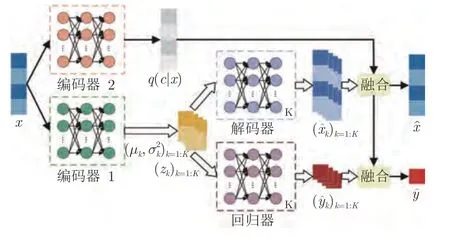
图2 混合变分自编码器回归模型结构图Fig.2 Model structure of the MVAER model

结合式(4)～ (6),模型的ELBO 可以重写为:

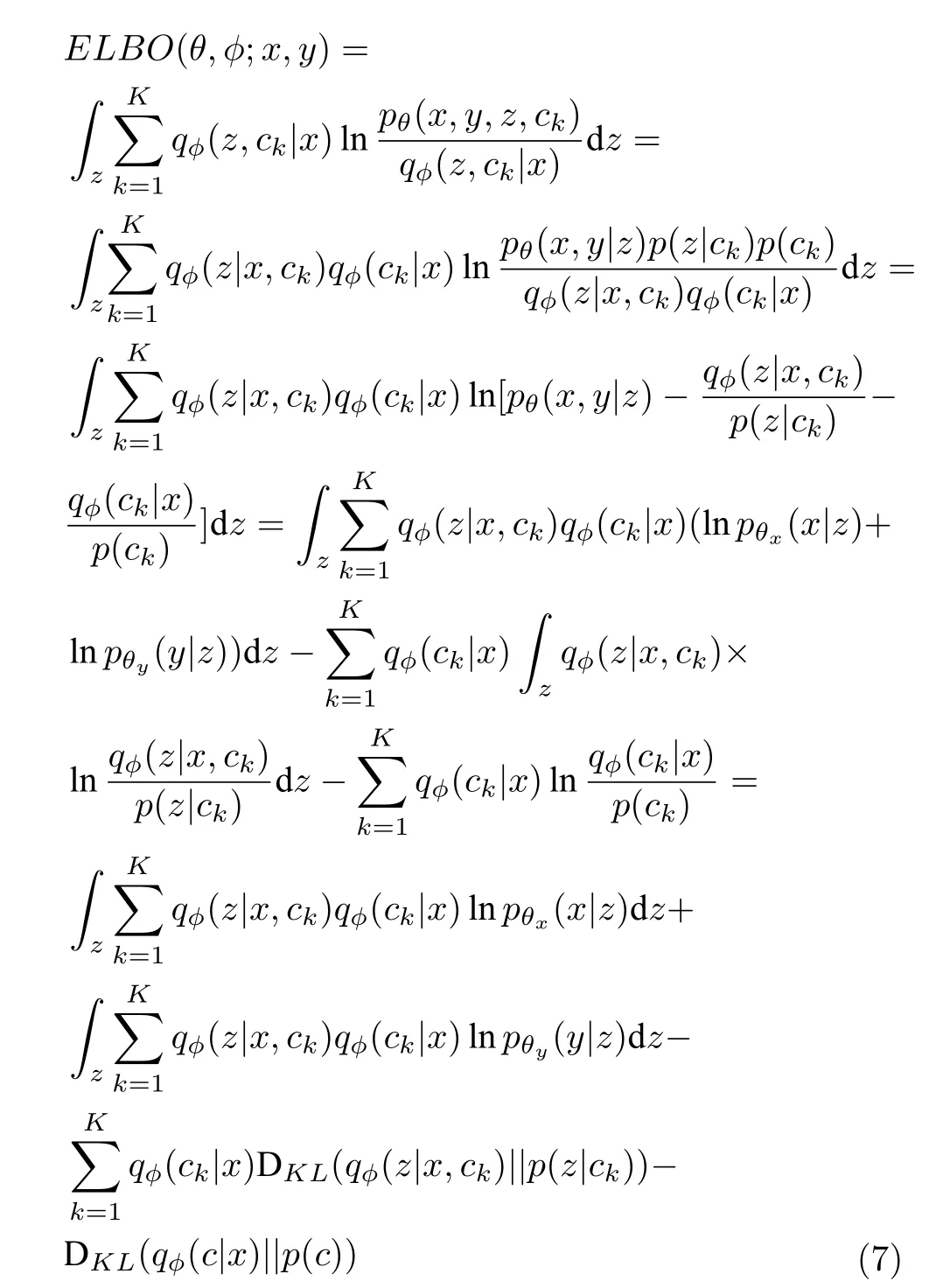
与VAE 相似,为了计算参数φ和θ,需要最大化上述的证据下界ELBO(θ,φ;x,y),这相当于最大化边缘概率似然函数.

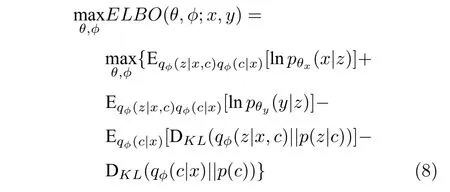
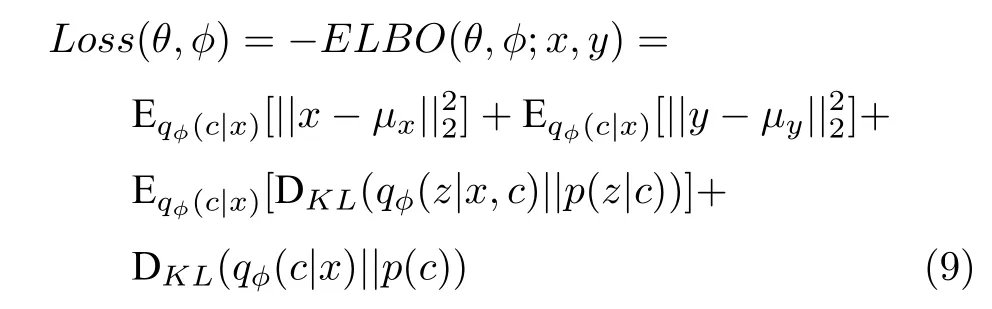
其中,μx通过模型解码器得到,μy通过模型回归器得到;表示数据在每个模式下的潜在特征所服从的高斯分布,其均值和方差通过模型编码器得到;qφ(c|x) 表示数据属于每个模式的可能性,通过带有Softmax 层的编码器计算得到.基于最小化损失函数的优化目标,可以通过随机梯度下降等优化算法,对模型参数φ和θ进行更新优化.

损失函数中的前两项是输入数据的重构误差和输出数据的预测误差项,能够鼓励模型很好地重构输入数据和预测输出数据;后两项是有关连续潜变量z和离散潜变量c的KL 散度项,有助于将原始数据中的变化传播到潜在空间中的隐变量中去,并使后验和先验之间更好地匹配.模型期望潜在空间中的离散隐变量c能够表示与原始混合分布中相对应的数据集群;潜在空间中的连续隐变量z能够表示每个集群内的数据变化.

2.2 基于MVAER 模型的在线软测量方法

在上一小节中,详细推导了MVAER 模型.当该模型用于工业过程在线软测量时,就是对当前样本,表示为xnew,提供相应的质量变量预测.

假设模型中p(y|z)=N(μy,k,I),其中z～q(z|xnew,ck),k=1,2,···,K,那么当前数据样本的质量变量预测值计算为:

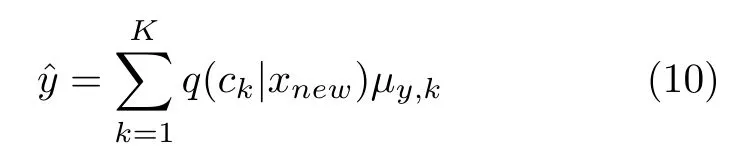
其中,q(ck|x) 表示当前数据样本属于第k个混合成分的可能性,可以通过模型中的编码器得到,计算公式如式(11)所示,公式中表示该编码器除最后Softmax 层之外的部分所代表的函数,则代表该部分的网络参数;μy,k表示当前样本质量变量y服从的高斯分布的均值,将其视为y的预测值,可以使用样本的潜在特征zk为输入,通过模型中的回归器得到,计算公式如式(12) 所示,公式中f(·;θy) 表示回归器所代表的函数,θy则代表回归器的参数.取所有混合成分下的预测值的加权和作为质量变量的最终预测值.

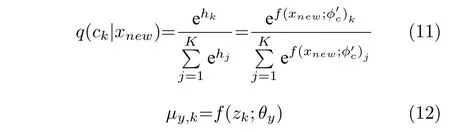
接下来,我们详细介绍基于MVAER 模型的实际工业过程软测量应用过程.该过程主要包括两部分,离线建模和在线预测.

在离线建模阶段,首先要根据理论分析和操作经验选择模型的输入变量,并采集数据(包括输入变量和质量变量).对收集到的数据进行标准化处理,然后训练MVAER 模型.当模型训练完成后,保存模型参数用于在线质量预测.在线预测时,对于新采集的待预测样本,需要对其进行与离线建模时相同的数据预处理,然后将其送入训练好的模型中,得到质量变量的预测结果.所提出的基于MVAER 模型的软测量建模算法总结如算法1 所示,并将整个过程直观地体现在如图3 所示的流程图中.

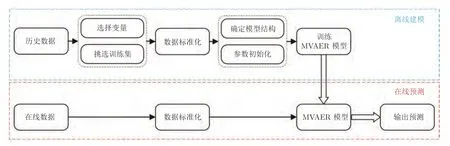
图3 基于MVAER 的软测量建模流程图Fig.3 Flowchart for soft sensor modeling based on the MVAER model

为了直观地评价模型的性能,本文使用均方根误差(Root mean squared error,RMSE)和R2系数两个指标来量化模型的预测效果.RMSE和R2定义如下:

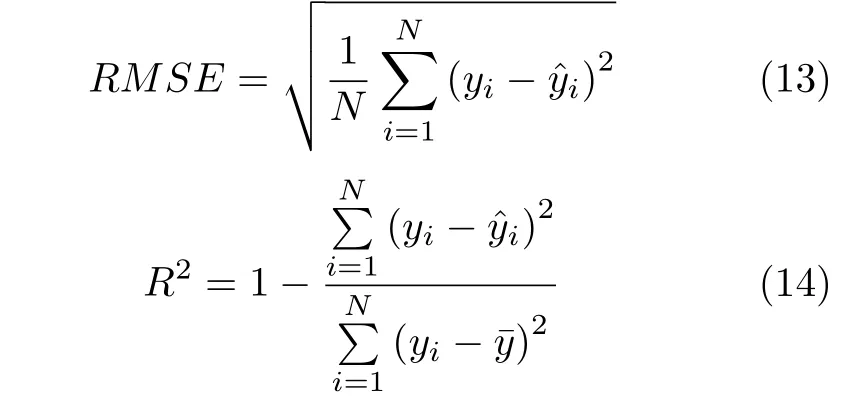
其中,N是样本个数,yi是第i个样本的实际输出值,是第i个样本的预测输出值,是所有样本实际输出值的平均值.RMSE 代表预测误差,R2表示实际值和预测值之间的平方相关关系.通常,RMSE越小,R2越接近于1,模型的预测性能越好.

3 案例分析

3.1 数值例子

本节设置了一个具有三种运行模式的数值算例,各个高斯组分和关系的具体情况如表1 所示.每个模式下输入和输出之间的关系都是非线性的.为了构建模型,生成500 个样本作为训练集用于模型训练,生成500 个样本作为测试集用于模型性能测试.图4 中分别显示了X和Y的数据分布,可以直观地看出该算例具有多模态行为.

表1 数值算例的配置Table 1 Configuration of the numerical example

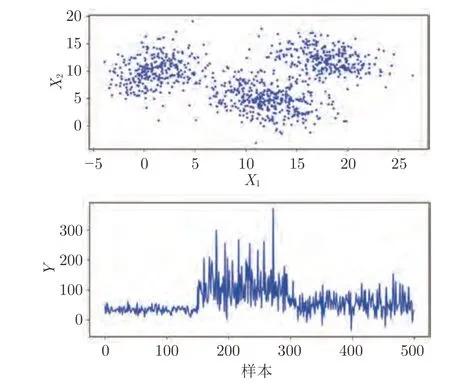
图4 数值算例的数据模式Fig.4 Data pattern of the numerical example

为了验证MVAER 算法的有效性,将其与偏最小二乘(Partial least squares,PLS)、高斯混合回归(Gaussian mixture regression,GMR)、自编码器(Auto-encoder,AE)、变分自编码器(Variational auto-encoder,VAE)方法进行比较.其中,PLS是一种传统回归模型,GMR 是一种典型的多模式建模方法,AE 是常用的深度学习建模方法,VAE则是所提出的MVAER 模型的基础框架.

在MVAER 算法中,将编码器和译码器设置为具有单层隐藏层,隐藏层的神经单元个数为6;潜在变量的维度设为2;为了方便,回归网络设为一个全连接层,即在提取的特征和输出之间建立一个线性关系;组分个数设为3,这是已知的.GMR 的组分个数设为3.每个模型在测试集上的数值评价指标在表2 中列出.

表2 PLS、GMR、AE、VAE和MVAER模型的性能评价指标Table 2 Performance evaluation indices of PLS,GMR,AE,VAE and MVAER models

从中可以发现,MVAER 模型的性能明显优于其他模型.PLS、GMR、AE、VAE和MVAER 的详细预测值如图5 所示,散点图如图6 所示.

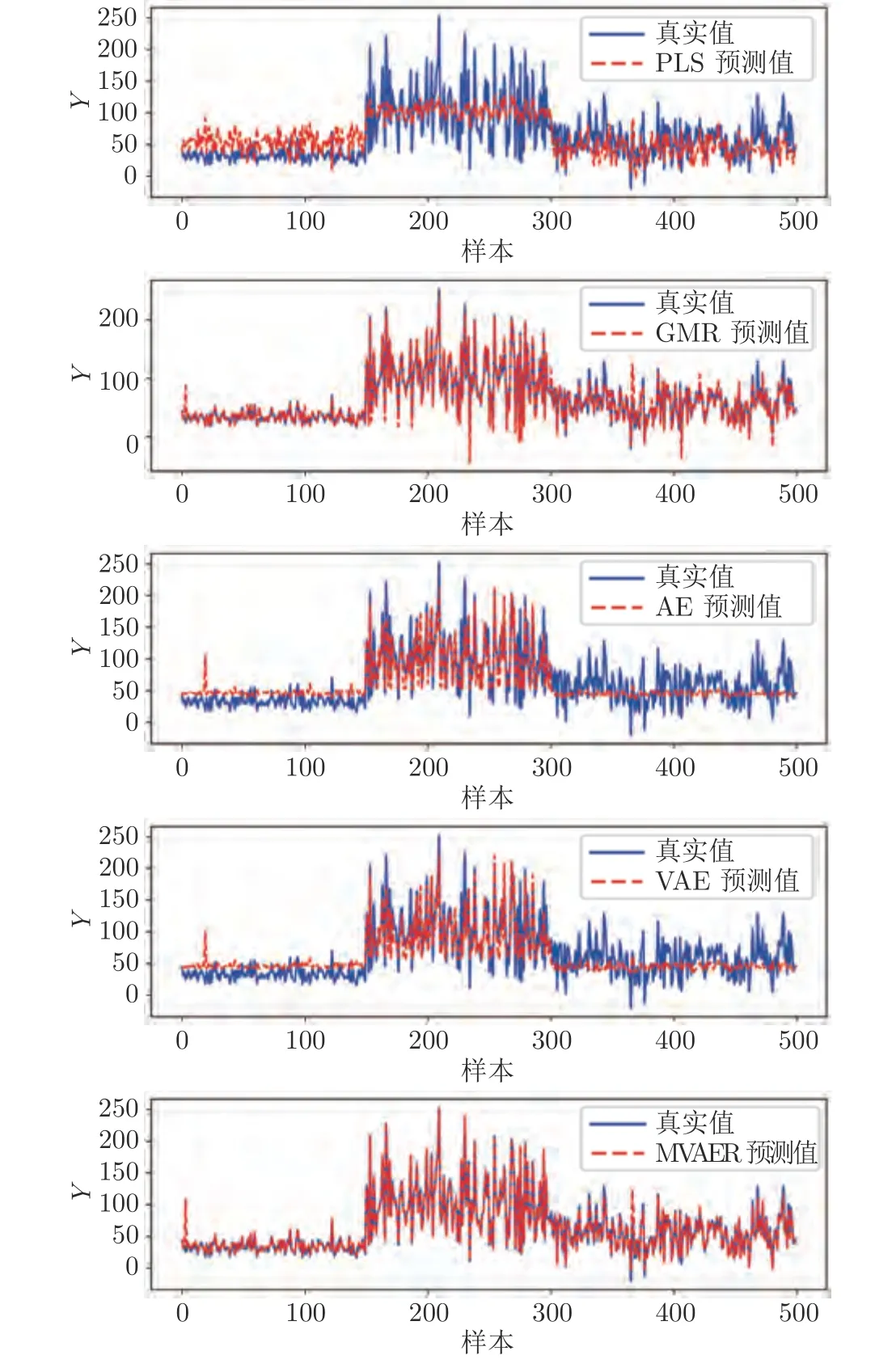
图5 PLS、GMR、AE、VAE和MVAER模型的预测结果图Fig.5 Predicted results of PLS,GMR,AE,VAE and MVAER models

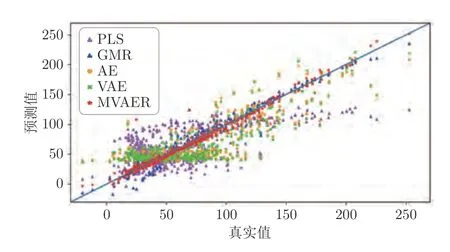
图6 预测结果散点图Fig.6 The predicted scatter points of different models

从预测曲线中可以直观地看出,PLS 在每个模态下都不能很好对输出值进行预测.相比之下,AE和VAE 模型对于该过程的回归预测效果有所改善,对第二模态样本有较好的预测效果.然而,AE和VAE 模型对第一模态和第三模态样本具有较差的预测能力,从图中可以看出在这两个模态下它们的预测结果趋于直线,这表明模型没有学习到相关的数据特性和耦合关系.GMR和MVAER 对所有模式下的数据样本都有良好的拟合能力,但与GMR相比,MVAER 的预测曲线更加贴合真实曲线,具有更高的预测精度.从散点图中,也能得到相似的结论.散点图结果表明,PLS 等模型的预测结果分布较为分散,存在较大的预测偏差,而MVAER 模型的预测结果更加集中和靠近主对角线,这意味着它的预测效果最好.以上比较和分析表明,PLS 作为线性模型,不能有效提取数据中的非线性和多模态特性,因此不能很好地处理具有复杂特性的过程,而 AE和VAE 模型虽然可以处理非线性关系,但无法同时对多个模态下的耦合关系进行建模.GMR和MVAER 模型则可以较好地适应多模态过程,并且当输入输出之间非线性相关时,MVAER 的性能优于GMR.

3.2 工业例子

该工业案例取自于合成氨过程中的制氢装置,氢气是合成氨气的重要原料之一.根据工艺设计,氢气生产过程中的关键反应在一段转化炉中进行,主要是通过脱碳反应将脱硫天然气转化为氢气.过程的工艺流程图如图7[28]所示.根据反应机理,温度对氢气的含量和纯度有很大的影响,而炉内温度主要取决于稠密燃烧器的燃烧条件.燃烧条件则是通过调节炉内氧气含量来控制的.因此,控制一段炉顶部氧气浓度在规定的范围内是十分重要的.在实际生产过程中,氧气含量通常由昂贵的质谱仪测量得到.为了降低生产成本,有必要构建一种软传感器在线估计氧气含量.

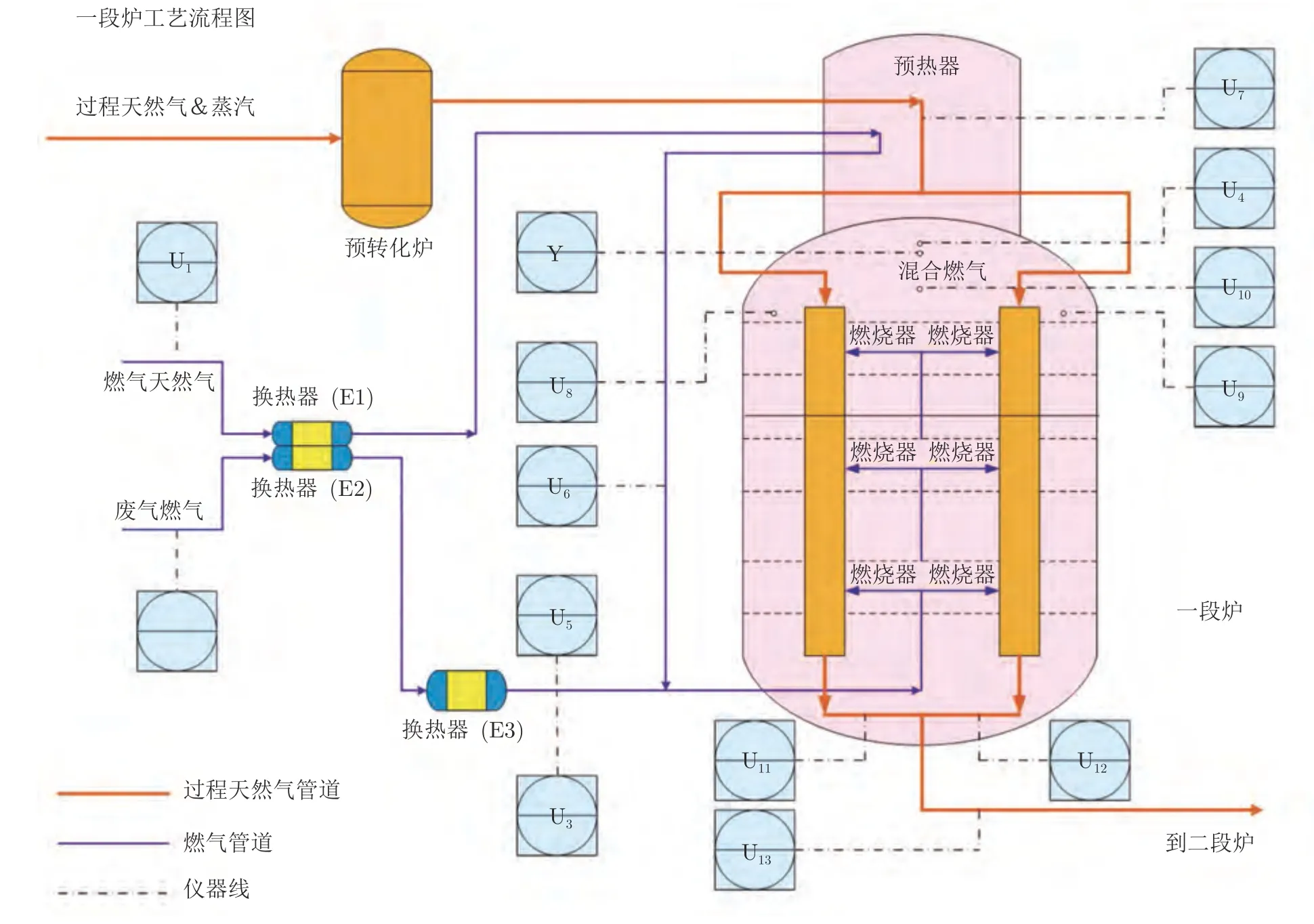
图7 一段炉工艺流程图Fig.7 Flowchart of the primary reformer

选择13 个过程变量作为软测量模型的输入变量,包括温度、流量和压力,它们易于测量且和氧气含量变化有关.这13 个过程变量的详细说明列于表3.收集5 000 个样本用于构建软测量模型,其中2 500 个样本作为训练集,其余样本作为测试集.为了展示MVAER 的有效性,构建PLS、GMR和VAE模型进行性能比较.通过试错方法,将MVAER 的组分个数K设置为4,编码器的隐藏层神经单元个数设置为32,隐变量的维度设为10,解码器的结构与编码器对称,回归器与上述数值算例中的一样,是一层全连接层.GMR 的组分个数设置为9.VAE 模型的结构参数与MVAER 中对应的参数保持一致.

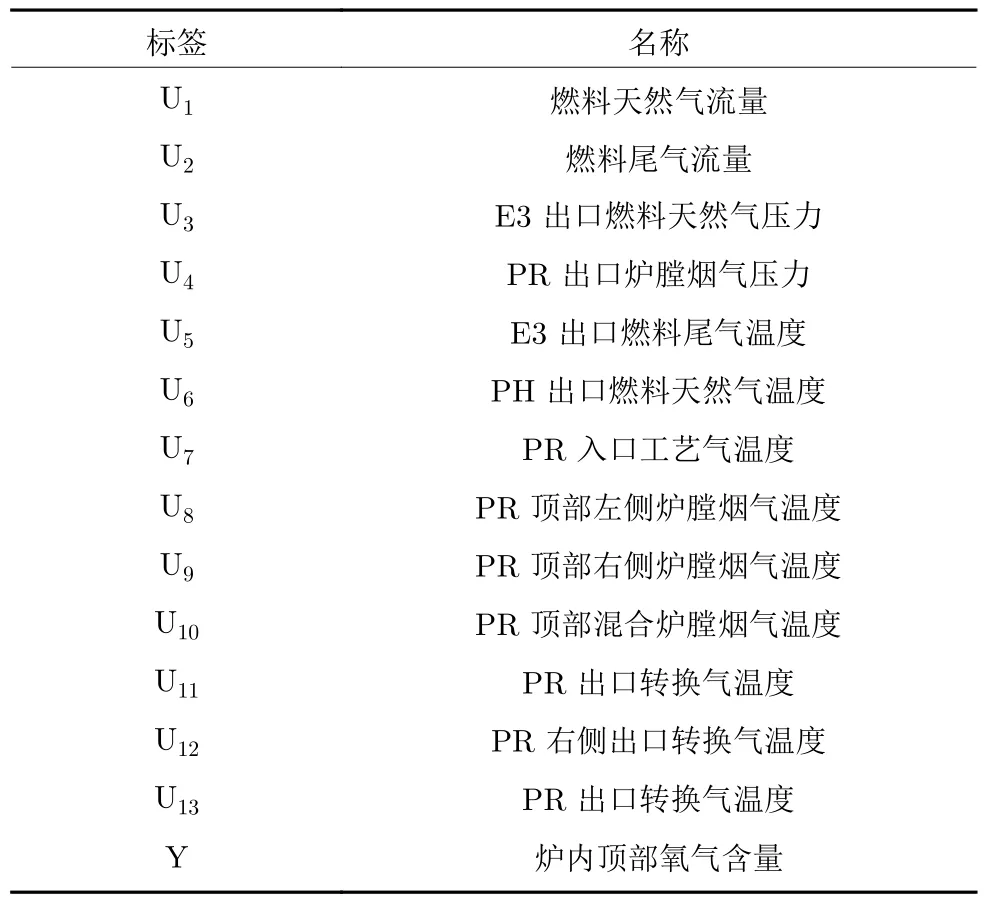
表3 一段炉过程变量描述Table 3 The description of the process instruments in the primary reformer

各种方法的性能评价指标,RMSE和R2,列于表4.通过比较这些结果可以发现,多模态建模方法优于非多模态方法,非线性方法优于线性方法.其中,MVAER 模型的预测性能最好.

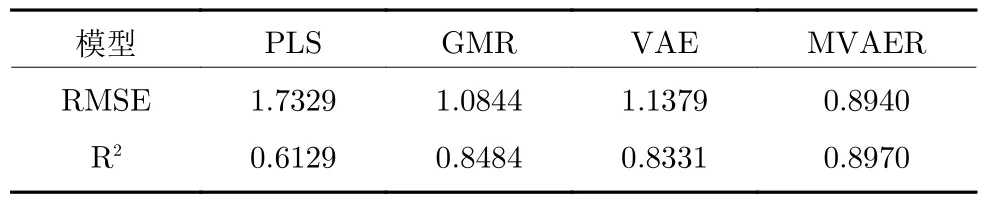
表4 PLS、GMR、VAE和MVAER模型的性能评价指标Table 4 Performance evaluation indices of PLS,GMR,VAE and MVAER models

PLS、GMR、VAE和MVAER 对氧气浓度的预测结果如图8 所示.直观上,从图中可以看出,PLS 模型的预测结果比较平稳,不能很好地追踪氧气浓度的变化.其余三种方法的预测效果都优于PLS 模型.其中,VAE 虽然大体上能捕捉氧气浓度的变化趋势,但其预测波动较大,预测曲线上有较多的毛刺;相比之下,GMR 模型能较好地对氧气浓度进行预测,但是其预测曲线存在较多的尖峰现象.与VAE和GMR 相比,MVAER 模型的预测效果则有了明显改善.MVAER 模型的预测曲线毛刺、尖峰现象更少,与真实值曲线吻合度较高,这意味着我们的模型有更强的拟合能力和更高的预测精度.几种模型的预测误差和预测散点图分别如图9和图10 所示,从中也能得到相似的结论.具体来说,图9 中显示MVAER 模型的预测误差小于其他几种方法,大多处于-2和+2 之间.图10 中显示,MVAER 模型的预测结果分布更加集中,并且最为接近主对角线,这些结果都反映出MVAER 模型具有较好的预测性能.

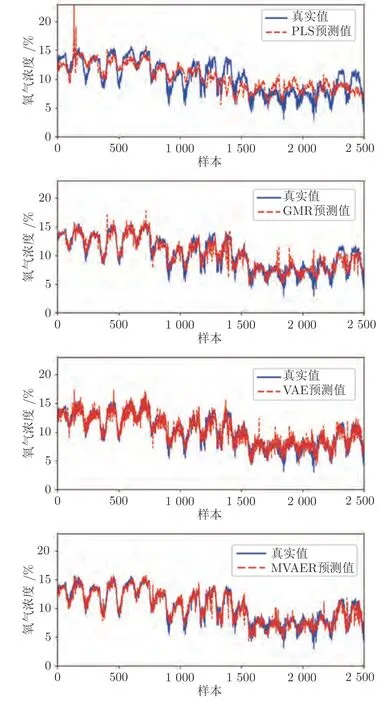
图8 PLS、GMR、VAE和MVAER 模型的预测结果图Fig.8 Predicted results of PLS,GMR,VAE and MVAER models

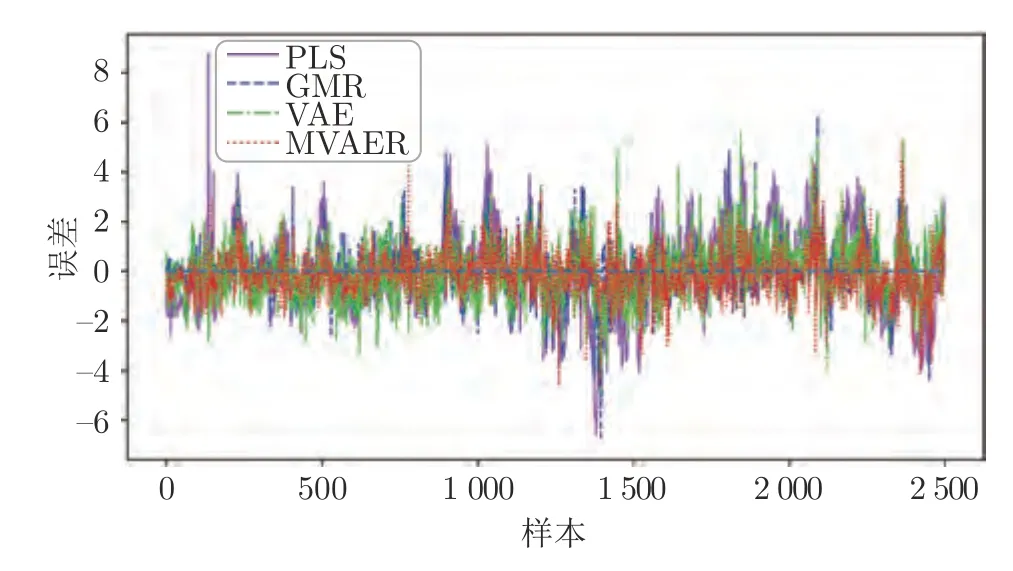
图9 预测误差图Fig.9 The prediction errors of different models

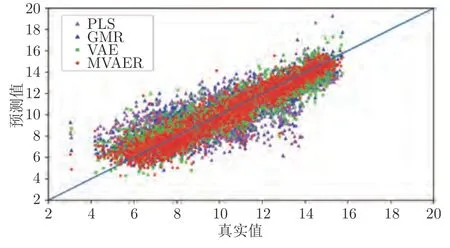
图10 预测结果散点图Fig.10 The predicted scatter points of different models

总体而言,以上两个实例的比较和分析表明,面对复杂多模态过程,本文所提出的MVAER 模型在捕获数据多模态特性和非线性等方面表现出较强的能力,能够有效地对关键质量变量进行预测.

4 结论

本文提出了一种新的混合变分自编码器回归模型,并将其用于复杂多模态工业过程的产品质量软测量.通过结合高斯混合模型的思想,该方法打破了传统VAE 中潜在空间单峰分布的限制,能够有效地提取复杂多模态数据的潜在特征,并利用潜在特征对产品质量变量进行回归建模.此外,该方法由于其混合概率框架,在不同模态下将会自动进行质量预测.在两个案例中,包括一个数值例子和一个合成氨生产过程一段炉实际工业过程,与其他几种方法相比,基于混合变分自编码器回归模型的软传感器预测性能最好,验证了所提方法的有效性和可行性.最后,考虑到过程数据中有标签数据稀少的实际情况,后续研究工作可以结合半监督学习,将所提方法扩展为半监督软测量方法.