带有资源冲突的Seru 在线并行调度算法

江煜舟 李冬妮 靳洪博 殷 勇

随着大规模定制发展的趋势,传统的生产系统,如流水线(Flow line)、丰田生产系统(Toyota production system,TPS)、作业车间(Job shop)、单元制造系统(Cellular manufacturing system,CMS)等,难以适应对动态不确定市场的快速响应需求,赛如生产系统(Seruproduction system,SPS)应运而生[1-3].

Yin 等[4]的研究展示了传统生产系统转化为SPS的重要性,Liu 等[5-6]的研究也表明SPS 具有传统生产系统难以企及的先进性和发展前景[7].自二十世纪九十年代起,SPS 已经逐渐被亚洲的众多电子企业采用,如三星、佳能、LG、索尼、松下、富士通、NEC、富士康等[8-10].

Seru代指SPS 下的最小生产单元,脱胎自基于精益(Lean)思想[11]的装配流水线,一个Seru通常是生产一种或多种产品的装配单元,包含若干设备和工人.

一个SPS 至少包含一个Seru.SPS 中的每一个Seru都能够频繁地在短时间内被重构,这给SPS 带来了极大的灵活性.可以快速频繁地建立、改变、拆除和转化,以响应频繁波动的市场需求[9-10].

SPS 运作管理的基本原则为面向 “组织”的准时生产原则(Just-in-time organisation system,JIT-OS),是TPS 传统的面向 “物料”的准时生产原则(Just-in-time material system,JIT-MS)的延伸.JIT-MS 指在合适的时间地点投入合适的物料,强调的是物料.而JIT-OS 强调的是组织,对应到SPS,即在合适的时间地点构建合适的Seru.这让SPS 可以通过调整生产组织结构快速获得相应的生产能力,为重构的实施提供了有效的载体和途径[1].

SPS 的运作可以被划分为Seru构建与Seru调度两个部分,Seru构建指如何依据订单任务对人员进行分配与组合,Seru调度指如何在有限的空间下安排各个Seru的构建顺序及时间,目前相关研究大都侧重于Seru构建.如Liu 等提出的解决工人分配问题的三段式启发模型[12]、Yu 等提出的以产品流通时间和总劳动时间为目标的一种非支配排序遗传算法[13]、Yu 等结合局部搜索算法提出的第二代非支配排序遗传算法[14]、吴旭辉等联合Seru构建与订单分配提出的一种协同进化算法[7]、贾凌云等[15]与田云娜等[16]对跨单元调度问题的研究等.

目前对Seru调度这一方面的研究相对较少,难以充分体现SPS 调整结构的动态性,但要想充分发挥出SPS 的灵活性,快速响应 “小批量,多品种”市场的动态变化,在提高Seru构建效率之外,还需要考虑结构上的变化,即Seru调度.如何在有限的位置上安排Seru的构建顺序及时间也是SPS 运作管理基本原则JIT-OS 的一项重要内容.

据此,本文对Seru在线并行调度问题展开了研究,该问题具体是指,将随时间动态构建的n个Seru安排到有限的m个位置上,以总加权完工时间最小为目标,在线决策各Seru的构建顺序及时间.同时,考虑到具体的生产环境,为了增强算法的实用性,本文还将对带有资源冲突的Seru在线并行调度问题进行讨论.

本文接下来的内容安排如下:第1 节,给出具体的问题模型;第2 节,给出AD-SWPT 算法优化后得到的具有良好常数竞争比的在线算法;第3 节,给出带有资源冲突的Seru在线并行调度算法,并计算特殊实例下算法的竞争比;第4 节,设计相关实验,展示实验结果,分析实验数据;第5 节为结论部分.

1 问题描述与分析

本文所研究的带有资源冲突的Seru在线并行调度问题是指,如何在有限个Seru的可用位置上在线安排多个带有资源冲突的Seru,以提高生产效率,具体描述如下:

有一系列的订单任务随着时间发布,每一个订单任务对应一个Seru,Seru间可能存在资源冲突,在无优先级的情况下,将它们安排到m个Seru的可用位置上进行处理,存在资源冲突的两个Seru不能同时被处理,每一个Seru都对应一个订单任务发布时间rj,一个处理时间pj和一个权重wj,所有关于Seru的信息在订单任务发布前都是未知的.同样,Seru的总数量也无法提前得知.

在线算法的优劣通常用它的竞争比ρ来评价(对任意实例,算法的目标函数值都不大于ρ倍的最优离线目标值).

问题的基本假设如下:

1)车间中有m个Seru的可用位置,共有n个订单任务会发布(m与n均为正整数);

2)所有发布的订单任务都可以被完成,不考虑由工人技术或车间规模限制而导致的拒单;

3)一个订单任务只能在一个Seru中完成,不考虑拆分;

4)一个Seru的可用位置同一时间段最多安排一个Seru;

5)一旦Seru构建完成,被安排到某一空的可用位置上,在结束任务前Seru的位置不会发生改变,任务进程不会被打断;

6)不考虑由工具损坏或自然灾害等不可控因素导致的生产中断;

7)车间24 小时运转不停工.

问题描述所需的符号变量如下:

t表示当前时间;

m表示Seru的可用位置数目;

j为Seru的序号索引 (j=1,2,3,···) ;

k为车间内Seru可用位置的序号索引 (k=1,2,3,···) ;

rj表示Seru对应的订单任务发布时间(rj≥0);

pj表示Seru的处理时间(pj＞0);

wj表示Seru的权重(wj≥0);

Sj表示Seru的构建时间(Sj≥rj);

Cj表示Seru的完工时间(Cj=Sj+pj).

决策变量:

目标量总加权完工时间的表示为:

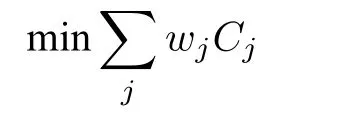
根据实际生产中的问题特性和约束,本文的约束条件描述如下:

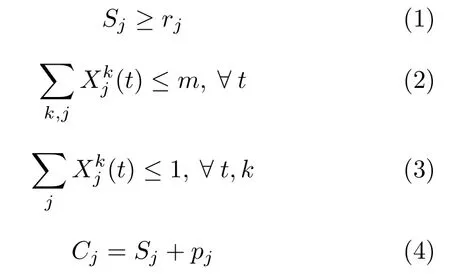
其中,式(1)表示订单任务发布之前,一切信息未知,无法构建相应Seru;式(2)表示任意时刻工厂内最多容纳m个Seru运作;式(3)表示任意时刻同一位置上最多容纳一个Seru运作;式(4) 表示Seru一旦构建,将会持续运作至完成订单任务,中途不会被打断.

目前尚无专门针对有资源冲突的Seru在线并行调度问题的相关研究,考虑类似的并行机调度问题构建.Seru的空间位置对应到并行机,将Seru安排在相应的位置上.并行机调度问题的跨领域应用在控制系统的故障诊断中也有体现[17-18].

对并行机调度问题,Anderson和Potts 率先提出了单机器下竞争比为2 的最优确定性在线算法,最小加权处理时间(Shortest weighted processing time,SWPT)算法[19].多机器下,Hall 等设计了一个竞争比为(4+ε)的算法[20],其中ε为任意小的正数.Megow和Schulz 将竞争比改进为3.28[21].Correa和Wagner 又提出了竞争比为2.618 的无优先级α调度(Non-preemptiveαscheduling,NAS)算法[22].Sitters 设计了 O NLINE(ε) 算法[23],并证明其竞争比不大于在并行机数量较少时该算法远优于NAS 算法,但在并行机数量增大时NAS 算法的竞争比趋近1.79,优于 O NLINE(ε) 算法.随机化被允许时,可以得到更好的算法,这里不再赘述[22,24-25].

通过推广Megow和Schulz 设计的单机器下的算法[21],Tao 提出一个以总加权完工时间最小为目标的并行机在线调度算法,即平均延迟最短加权处理时间(Average delayed shortest weighted processing time,AD-SWPT) 算法,算法竞争比为(2.5-1/(2m))[26].对AD-SWPT 进行改进,Tao 等提出一个竞争比为4m) 的算法[27],是目前文献中以总加权完工时间最小为目标的并行机在线调度算法中竞争比最小的一个.但无论是AD-SWPT 算法还是其改进算法,所得到的竞争比都不是一个常数,后者还极为复杂.

先基于AD-SWPT 算法及其改进算法得到一个竞争比为常数的算法,有利于将原本针对于并行机调度问题的算法应用于SPS,以及在无资源冲突的Seru在线并行调度算法上添加冲突机制后对算法性能展开数学上的理论分析.

非常数的竞争比会让对带有资源冲突的Seru在线并行调度算法竞争比的计算变得更加复杂,甚至难以推进.同时,一个具有常数竞争比的算法也能为本领域及并行机调度等相关领域的后续研究提供更加便捷与直观的参照.

因此,本文针对Seru在线并行调度问题,首先考虑无资源冲突的情况,对AD-SWPT 算法竞争比不为常数的局限性,设计α

AD-SWPT 算法,采用实例归约的方法来计算竞争比,得到一个具有良好常数竞争比的算法,再在αAD-SWPT 算法的基础上,针对带有资源冲突的Seru在线并行调度问题,将问题转化为计算具有特殊结构实例的竞争比,可以得到某些特殊情况下的优化算法.

2 α AD-SWPT 在线算法

2.1 AD-SWPT 算法简介

AD-SWPT 算法.对并行机的在线调度问题,一旦出现空机器和一些可以被安排的任务时,在所有已生成但未安排的任务中,选择处理时间与权重比值pj/wj(后文中用加权处理时间来代指这个比值)最小的一个.当出现相等的情况时,选择处理时间较小的.记被选择的任务为Ji,计算时刻t所有机器上正在运作的任务的剩余处理时间总和.这个值根据表1 中的符号可以被写作.那么如果

表1 基本符号说明Table 1 Basic symbolic explanation

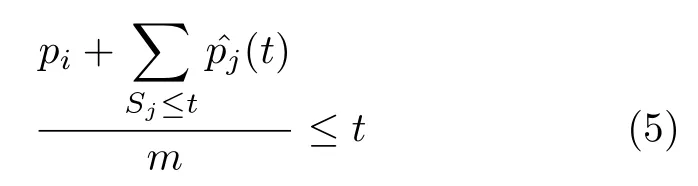
就在t时刻将Ji安排在空机器上;否则,等下一个时刻重复以上整个过程.

对一般情况下AD-SWPT 算法的竞争比,有:

定理1[26].对以总加权完工时间为目标量的无优先级并行机在线调度问题,AD-SWPT 算法的竞争比区间为 [2,2.5-1/(2m)].

定理1 的证明采用了实例归约,该思想在对两个半在线单调度问题的分析中被首次提出[28-29].在证明中发现,AD-SWPT 算法可以被进一步优化.

2.2 α AD-SWPT 算法简介

AD-SWPT 算法的竞争比(2.5-1/(2m))不为常数,而其优化算法的竞争比4m),虽然在数值上略有减小,却更为复杂.于是,本文在AD-SWPT 算法的基础上,设计了一种竞争比为常数的调度算法.记为αAD-SWPT (α-average delayed shortest weighted processing time)算法.

在式(5)右侧添加调节参数α(当α=1 时,优化算法退化为AD-SWPT 算法,m→∞时,新发布的任务无需等待可立即被安排,可以认为α＞1[27]),将t变为αt,同时将并行机的调度问题,对应到Seru的调度问题上,如图1 所示.AD-SWPT 算法变化如下:

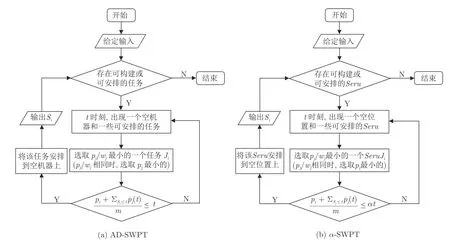
图1 AD-SWPT 与 α AD-SWPT 算法流程图Fig.1 The flow charts of AD-SWPT and α AD-SWPT

α AD-SWPT 算法.一旦出现空位置和一些可以被构建的Seru时,在所有对应订单任务已发布但未构建的Seru中选择加权处理时间pj/wj最小的一个.当出现相等的情况时,选择处理时间较小的.记被选择的Seru为Ji,计算时刻t所有位置上正在处理的Seru的剩余处理时间总和.这个值根据表1 中的符号可以被写作.那么如果

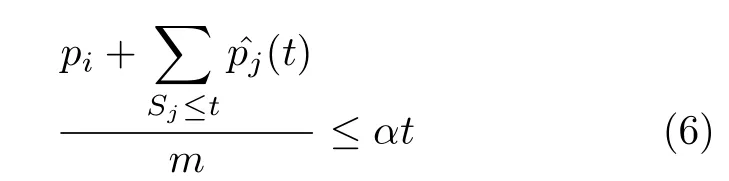
就在t时刻将Ji安排在空位置上;否则,等下一个时刻重复以上整个过程.

2.3 α AD-SWPT 算法竞争比的计算

尽管竞争比是指在所有可能的实例中所能达到的最坏性能比,但穷举搜索是不可能的,因为集合所包含的实例数目是无穷的.

性能比与竞争比的概念类似,在接下来的证明过程中,为了不至于造成误解,将非一般实例集合下的竞争比称为性能比.

αAD-SWPT 算法竞争比的计算方法与ADSWPT 算法同源[26],同样采用实例归约.

实例归约的思路是在实例空间中找出最坏的情况,证明部分实例的竞争比不小于其他实例,从而缩小搜索空间,在更小的集合内对算法的性能比进行分析.这些更小集合里的实例拥有的特殊性质,可以使对性能比计算的分析更加深入.

本文中,最坏的情况可能从两类实例集中得到.可以推测,这两类实例性能比的表达式中含有调节参数α.

2.3.1 相关定义与性质

αAD-SWPT 算法中由于存在延迟机制,所以在一些位置上会出现空余的时间段.

为了方便叙述,参考AD-SWPT 算法竞争比计算中的定义[26]:

称一个位置在时刻t为 “闲置”,如果这个位置在时间段 (t-ε,t+ε) 闲置;称一个位置在时刻t为 “运作”,如果这个位置在时间段 (t-ε,t+ε) 不闲置,其中ε为无穷小的正数.

称时刻t是一个位置的 “运作起点”(记为SPoint),如果这个位置在时间段 (t-ε,t) 闲置,在时间段 (t,t+ε) 不闲置;称时刻t是 一个位置的“运作终点”(记为EPoint),如果这个位置在时间段(t-ε,t) 不闲置,在时间段 (t,t+ε) 闲置.

根据Tao 在论文中的描述,可以证明,最坏情况下的实例在αAD-SWPT 算法下产生的调度方案中,所有位置最早的SPoint和最晚的EPoint 之间,不存在时刻t,满足所有位置都在时刻t闲置[26].

记满足上述性质的实例为I1.

σ(I1) 中的Seru按照构建时间排列,记作J1,J2,···,Jn.以队列内Seru的加权处理时间非减为原则,可将Seru分割为若干个子队列,每个子队列最后一个Seru的加权处理时间大于下一个子队列第一个Seru的加权处理时间,如图2 所示.

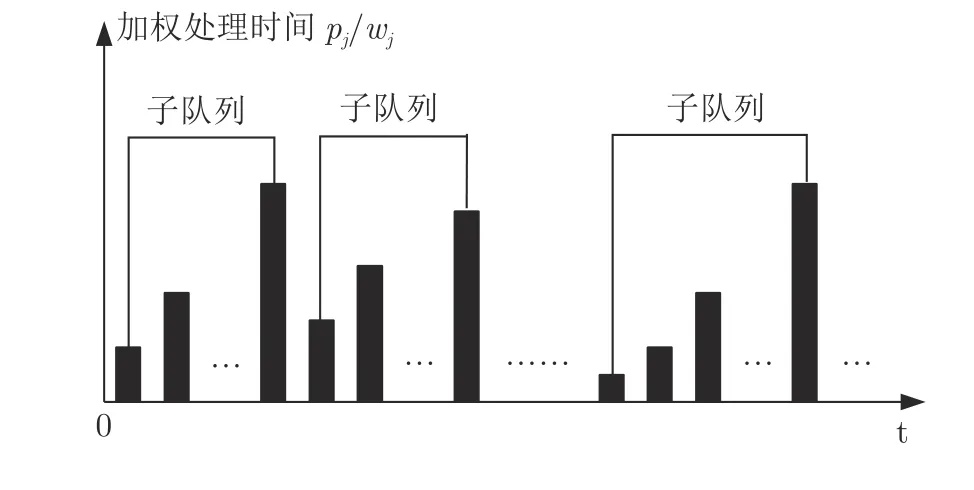
图2 按照 α AD-SWPT 安排方案的构建时间示意图Fig.2 Processing sub-queues in terms of starting time in the α AD-SWPT schedule

2.3.2 实例归约

首先引入一个重要引理[28],这个引理会在接下来的分析中被反复使用.

引理1.f(x)和g(x) 是定义在区间 [u,v] 上的两个正值函数,且f(x) 为凸函 数,g(x) 为凹函 数.f(x)/g(x) 的最大值在区间端点处取到,即:

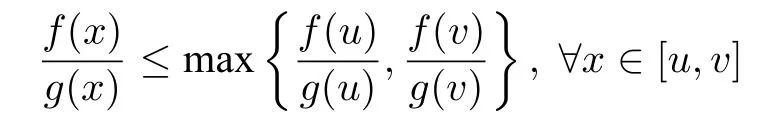
证 明.∀x ∈[u,v],∃a∈[0,1],s.t.x=au+(1-a)v.又f(x) 为凸函数,g(x) 为凹函数,那么有:

f(x)≤af(u)+(1-a)f(v)

g(x)≥ag(u)+(1-a)g(v)

又f(x)和g(x) 是定义在区间[u,v] 上的两个正值函数,那么有:

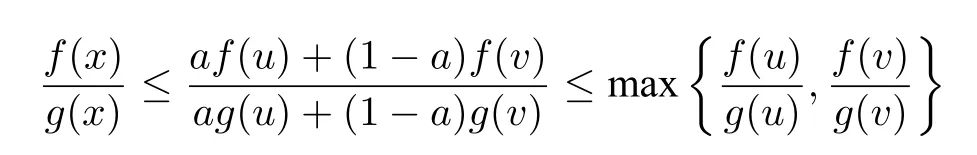
可以证明,在区间的某个端点开放时引理也成立,此时f(x)/g(x) 的上确界存在于相对应的端点处.□

按照Tao 的处理方式,将I1在性能比不减的情况下,化归为两类特殊实例,它们在αAD-SWPT 算法下生成的安排方案具有更多简单特殊的子队列结构.

第一类,实例中的Seru拥有相同的加权处理时间,记作I2;第二类,实例中部分Seru的权重趋近于无穷大,记作I3.

记为一个过渡实例,它在αAD-SWPT 算法下生成的安排方案满足最后一个子队列中所有Seru具有相同的加权处理时间.

直接引用Tao 在论文中给出的定理,有:

表2 无冲突时的特殊实例符号说明Table 2 Symbolic explanation of four special instances without conflicts

引理2[26].对任意实例I1,都能通过修改I1中Seru的权重来找到一个过渡实例,使得:

引理3[26].对任意实例,都能通过修改中Seru的权重来构建一个实例I2或I3,使得:

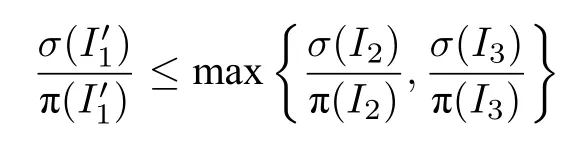
2.3.3 竞争比的计算

引理4.在αAD-SWPT 算法下,对于特殊实例I2,有:

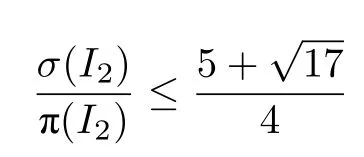
证明.参考Tao 在计算AD-SWPT 算法下竞争比时的推理过程[26],在不影响性能比大小的情况下,对I2中所有的Seru进行标准化.

记σ(I2) 中最后一个SPoint 为rL,在rL之后,每一个位置上Seru都被连续安排,不存在有位置空闲的时间段.下面分为两种情况讨论:

1) 在σ(I2) 中不存在对应订单任务先于rL发布,但于rL或之后构建的Seru.将σ(I2) 中于rL或之后构建的Seru,按照构建时间的顺序排列,记为J1,J2,···,Jn,剩余Seru构成的过渡实例记为.

2)在σ(I2) 中存在至少一个Seru,对应订单任务于rL之前发布,但于rL或之后构建,记为Jk.

将σ(I2) 中于rL或之后完成的Seru,按照构建时间的顺序排列,记为J1,J2,···,Jn,剩余Seru构成的过渡实例记为.

将{J1,J2,···,Jn}分为如下两个集合:

引理5.在αAD-SWPT 算法下,对于特殊实例I3,有:

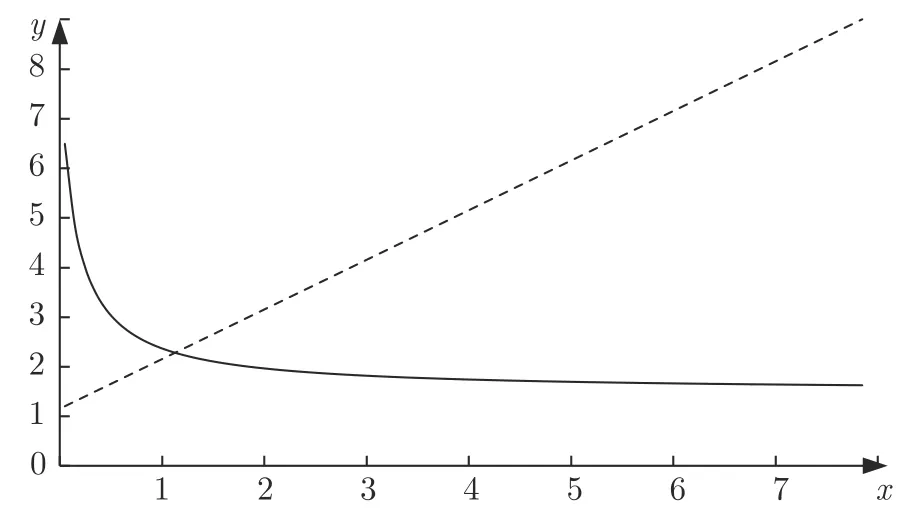
图3 f (α) 与 g (α) 的图像Fig.3 Graphs of f (α) and g(α)

证明.参考Tao 在计算AD-SWPT 算法下竞争比时的推理过程[26],将σ(I3) 中最后一个子队列中所有Seru的集合记为Q∞,将Q∞中最早发布的订单任务的发布时间记为rf,将σ(I3) 中最后一个SPoint 记为rL.下面分为三种情况讨论:

1)rL≤rf.

将Q∞中的Seru按照构建时间的顺序排列,记为J1,J2,···,Jn.记.可以得到σ(I3) 的一个上界以及 π (I3) 的一个下界:

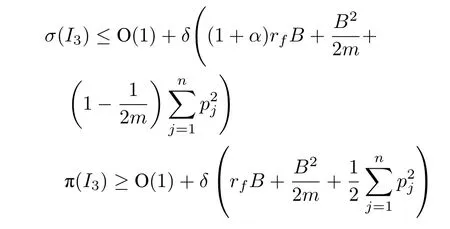
其中 O (1) 表示一个有限的数值.

当δ→+∞时,显然有:

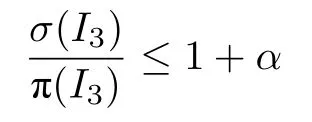
2)rL＞rf,且σ(I3) 中所有于rL时刻运作的Seru全部属于Q∞.剔除I3中的某些Seru,可以得到rL不是最后一个SPoint 的过渡实例,进而有:

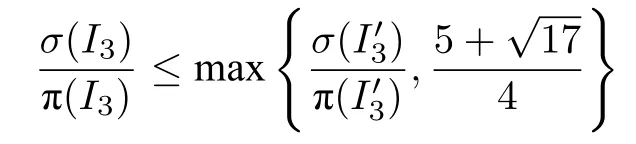
3)rL＞rf,且σ(I3) 中 于rL时 刻运作的Seru中至少存在一个不属于Q∞.下面再分为两种情况讨论:

a) 在σ(I3) 中,Q∞中不存在对应订单任务于rL之前发布,但构建于rL或之后的Seru.这种情况下,所有对应订单任务于rL或之后发布的Seru也于rL或之后构建.从I3中剔除这些Seru之后可以得到一个过渡实例.

b) 在σ(I3) 中,Q∞中至少存在一个对应订单任务于rL之前发布,且构建于rL或之后的Seru.

将σ(I3) 中,于rL时刻运作,但不属于Q∞的Seru组成的集合记为Q′.根据αAD-SWPT 算法,这些Seru一定于rf之前构建.

将Q∞中于rL之后完成的Seru分为如下两个集合:

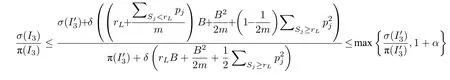
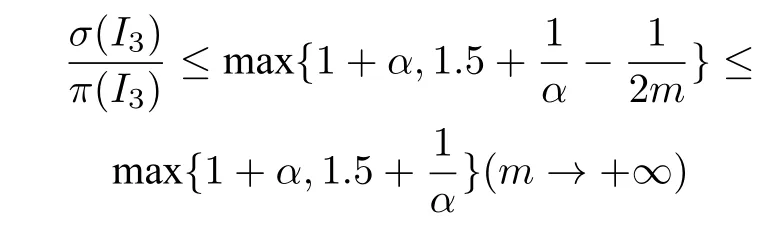
同引理4 的证明,可以得到:

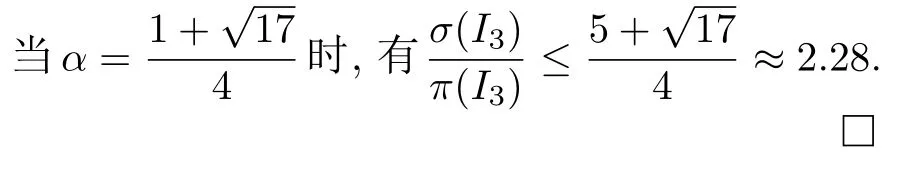
从而有如下定理:

引理2.对无资源冲突的Seru在线并行调度问题,αAD-SWPT 算法的最优竞争比在α=(1+时取得,为

图4 给出了AD-SWPT 算法、AD-SWPT 的改进算法以及αAD-SWPT 算法的竞争比对比图,可以看出与AD-SWPT 算法比较,虽然Seru的可用位置数目m=1,2 时,αAD-SWPT 算法竞争比偏大,但是到m＞2 时,AD-SWPT 算法的竞争比不断增大,竞争比恒为常数的αAD-SWPT 算法的性能明显更优.

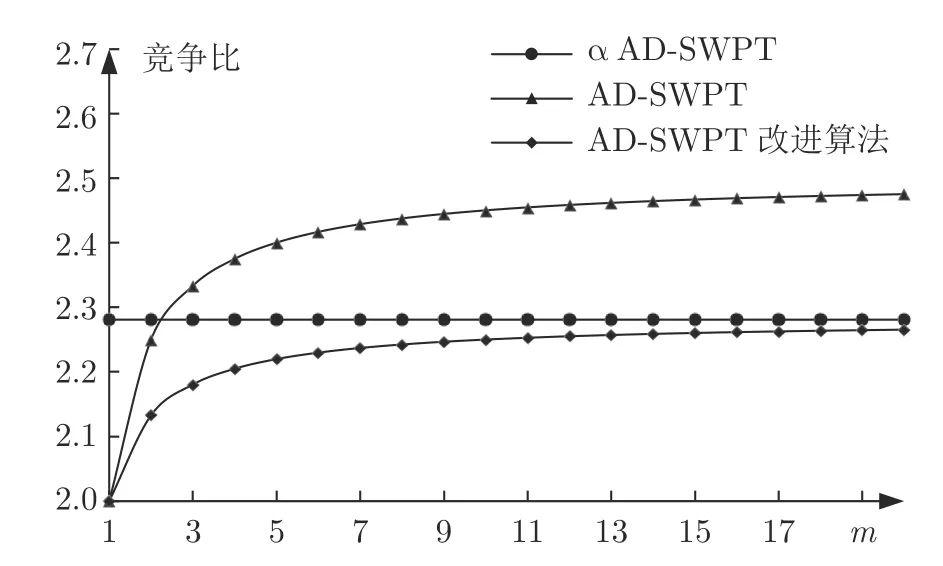
图4 三个算法的竞争比Fig.4 Graphs of each algorithm＇ competitive ratio

而αAD-SWPT 算法的竞争比虽略大于A DSWPT 的改进算法,不具有竞争比上的绝对优势,但随着m的增大,二者之间的细微差距在不断缩小,直至可以忽略不计.对此,后文会通过计算机模拟实验在有资源冲突的情况下进行验证.

3 存在资源冲突时的特殊情况

3.1 特殊情况的介绍

若有两个Seru由于人力资源或物力资源上的冲突,不能同时被安排,就称这两个Seru是具有资源冲突的.记本文所设计的带有资源冲突情况下的调度算法为αAD-I (α-average delayed shortest weighted processing time-improved)算法.

α AD-I 算法.一旦出现空位置和一些可以被安排的Seru时,在所有对应订单任务已发布但未构建的Seru中选择加权处理时间pj/wj最小的一个.当出现相等的情况时,选择处理时间较小的.记被选择的Seru为Ji,计算时刻t所有位置上正在处理的Seru的剩余处理时间总和.这个值根据表1中的符号可以被写作.那么如果

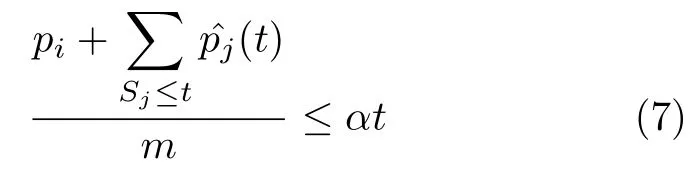
并且Ji与正在运作的Seru间无资源冲突,就在t时刻将Ji安排在空位置上;否则,等下一个时刻重复以上整个过程.

沿用实例归约的方法,对有资源冲突的Seru在线并行调度问题展开讨论,对具有特殊结构的实例进行竞争比的计算.

将αAD-I 算法构建的Seru中具有资源冲突的Seru记为冲突集合F.若存在这样的实例,F中先构建的Seru Jv与后构建的Seru Jk完工时间的比值满足pv/pk≤(1+1/m)/2,则记这样的实例为I*.

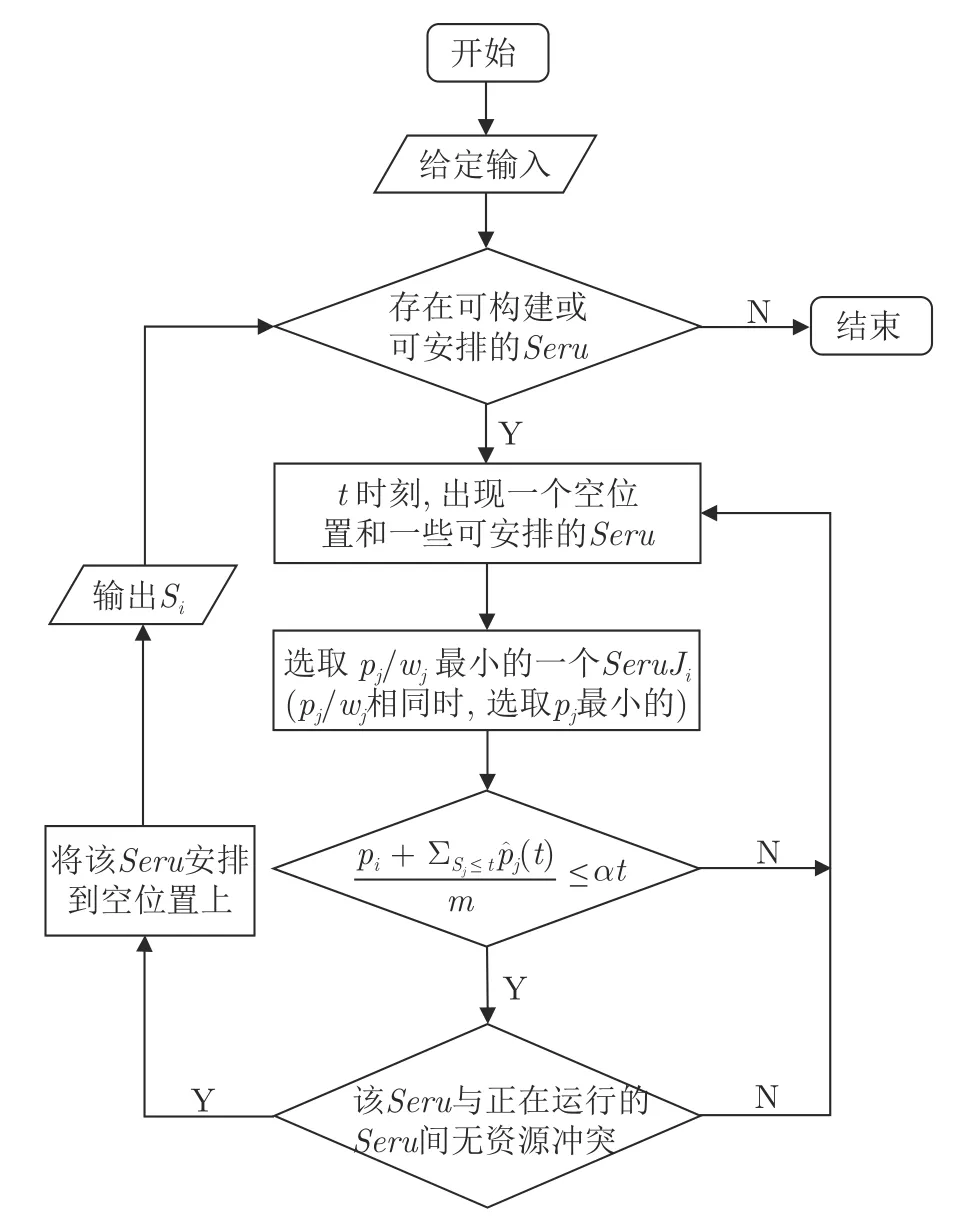
图5 α AD-I 算法流程图Fig.5 The flow chart of α AD-I

3.2 α AD-I 算法竞争比的计算

显然,对于I*,第2.3.2 节和第2.3.3 节中的分析都是适用的.那么有如下引理:

引理6.对任意实例I*,都可以通过将I*中部分Seru提出,以及修改权重来构建出一个实例或,使得:

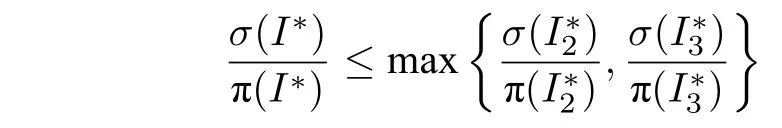
引理7.在αAD-I 算法下,对于特殊实例,有:

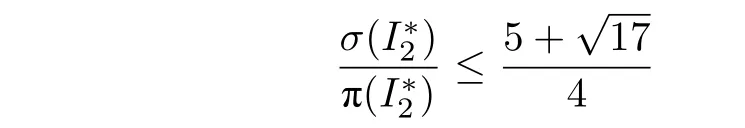
证明.σ() 中,同引理4 的证明,在不影响性能比大小的情况下,对中所有的Seru进行标准化,考虑σ(I2) 中最后的一个SPoint,记为rL.也就是说,在rL之后,每一个位置上Seru都被连续安排,不存在有位置空闲的时间段.

引理4 的证明分为了两种情况讨论,显然,情况1)下的证明不会发生改变.

而对情况2),对于对应订单任务在rL之前发布,但构建于rL或之后的所有Seru,若存在一个Seru使得式(6)不成立,证明过程不会发生改变;若对其中的任意Seru,式(6)均成立,根据αAD-I算法,有:

在该类子情况下,存在一个Seru,记为Jk,对应订单任务于rL之前发布,但构建于rL或之后,Jk∈F.将F中于rL时刻运作的Seru记为Jv,则pv/pk≤(1+1/m)/2 .

将于rL或之后构建的Seru,按构建时间顺序排列,记为J1,J2,···,Jn.

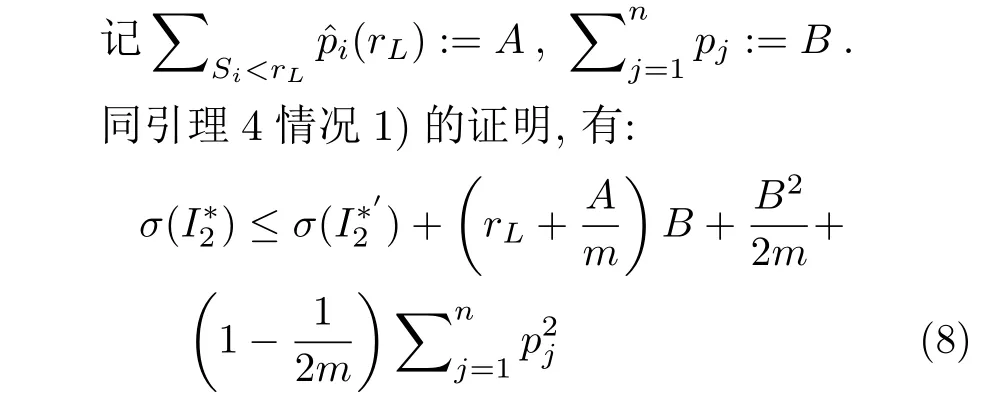
将{J1,J2,···,Jn}{Jk}视作一 个单独的实例,且将其中所有Seru的对应的订单任务发布时间放缩到rL.同引理4 情况1)的证明,可以给出π() 的一个下界:

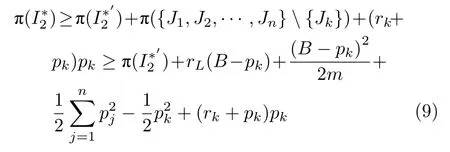
又rk＞rL-pv,因为加权处理时间相同时会选择处理时间较小的Seru来安排,那么根据式(7)、式(8),有不等式如本页下方所示.

再结合 (pk+A)/(αm)≤rL,以 及pv/pk≤(1+1/m)/2 .最终有:

引理8.在αAD-I 算法下,对于特殊实例,有:

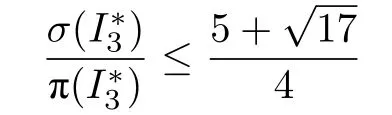
证明.σ() 中,最后一个子队列所有Seru的权重趋近于无穷,同引理5 的证明,将σ() 中最后一个子队列中所有Seru的集合记为Q∞,将Q∞中所有Seru间最早的订单任务发布时间记为rf,将σ() 中最后一个SPoint 记为rL.

引理8 的证明分为了三种情况讨论:

1)rL≤rf,证明同引理5 情况1).可得:

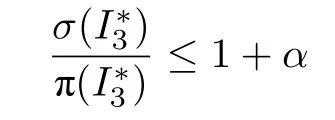
2)rL＞rf,且σ() 中于rL时刻运作的Seru全部属于Q∞,证明同引理7,从剔除掉一部分Seru后可得到rL不为最后一个SPoint 的过度实例.可得:

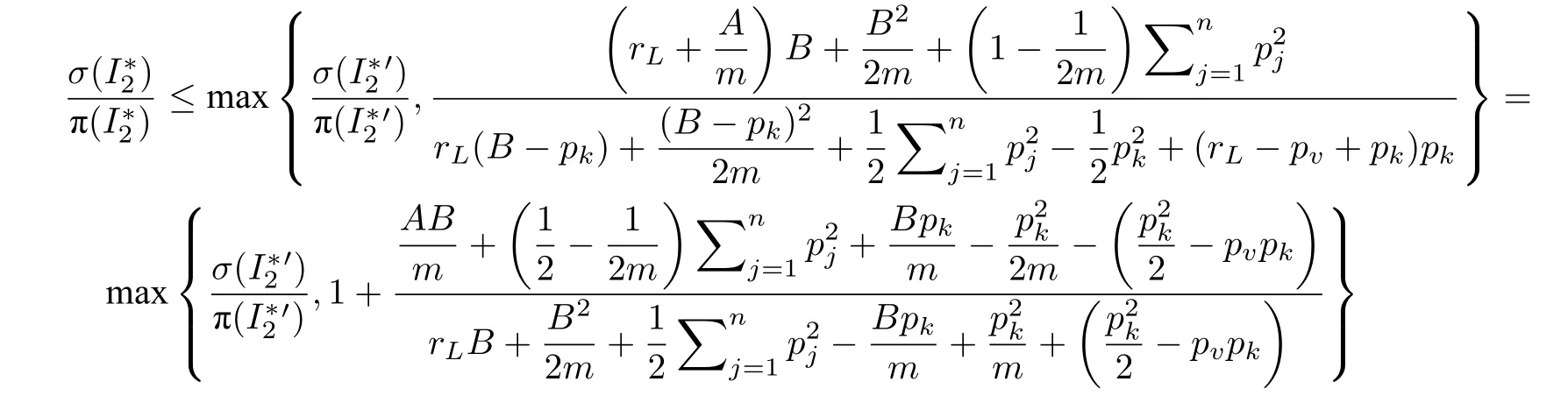
表3 有冲突时的特殊实例符号说明Table 3 Symbolic explanation of four special instances with conflicts

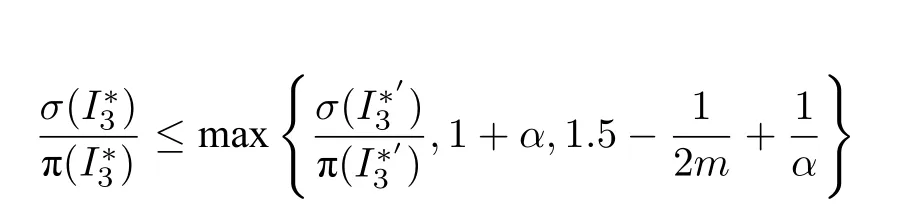
3)rL＞rf,且σ(I3) 中于rL时刻运作的Seru中至少存在一个不属于Q∞,再分为两种情况:

a) 在σ(I3) 中,Q∞中不存在对应订单任务于rL之前发布,但构建于rL或之后的Seru.且所有于rL或之后构建的Seru所对应的订单任务也于rL或之后发布,从I3中剔除这些Seru得到过渡实例,证明同引理5 情况3) a).可得:

4 实验与分析

4.1 特殊实例 I* 下 α AD-I 算法的性能检测

本节对特殊实例I*下αAD-I 算法的性能进行检测,在NAS 算法[22]以及 O NLINE(ε) 算法[23]中加入与αAD-I 算法相同的冲突处理机制,通过计算机实验比较I*下三个算法的性能.

参考Savelsbergh 等[30]以及Gu[31]在论文中采用的方法构建测试用例.对于不属于冲突集合F的Seru,订单任务发布时间按照参数为λ的泊松分布随机生成,λ为单位时间内平均发布的订单任务个数.对应低、平均、高三种不同的负载,将λ分别取为0.5、1.0和3.0;Seru的处理时间和权重从[1,100]中随机生成.

对于属于冲突集合F的Seru,订单任务发布时间和权重从[1,100]中随机生成,处理时间按照I*的定义生成,先构建Seru与后构建Seru完工时间的比值不大于 (1+1/m)/2 .

再考虑位置数目m,不属于F的Seru数目n1,以及属于F的Seru数目n2之间的不同组合.

取m∈{2,5,10,20,50},

n1∈{m,2m,4m,50,100,200},

n2∈{2,3,4,5},

λ ∈{0.5,1.0,3.0},

且n1≥n2,则共有312 种不同的组合,每一种负载下有104 种组合.

按照上述规则,每组随机生成1 000 个测试用例,定义Seru的处理时间除以m后单机器下最优算法SWPT[19]的目标值为模拟最优解,计算αADI 算法、添加冲突处理机制后的NAS 以及 ONLINE(ε)算法下的目标值与相应模拟最优解的比值,称其平均值为模拟竞争比.

结果如图6 所示,纵坐标为模拟竞争比,横坐标是不同的组合,按m、n1、n2的主次排序依据升序排列.

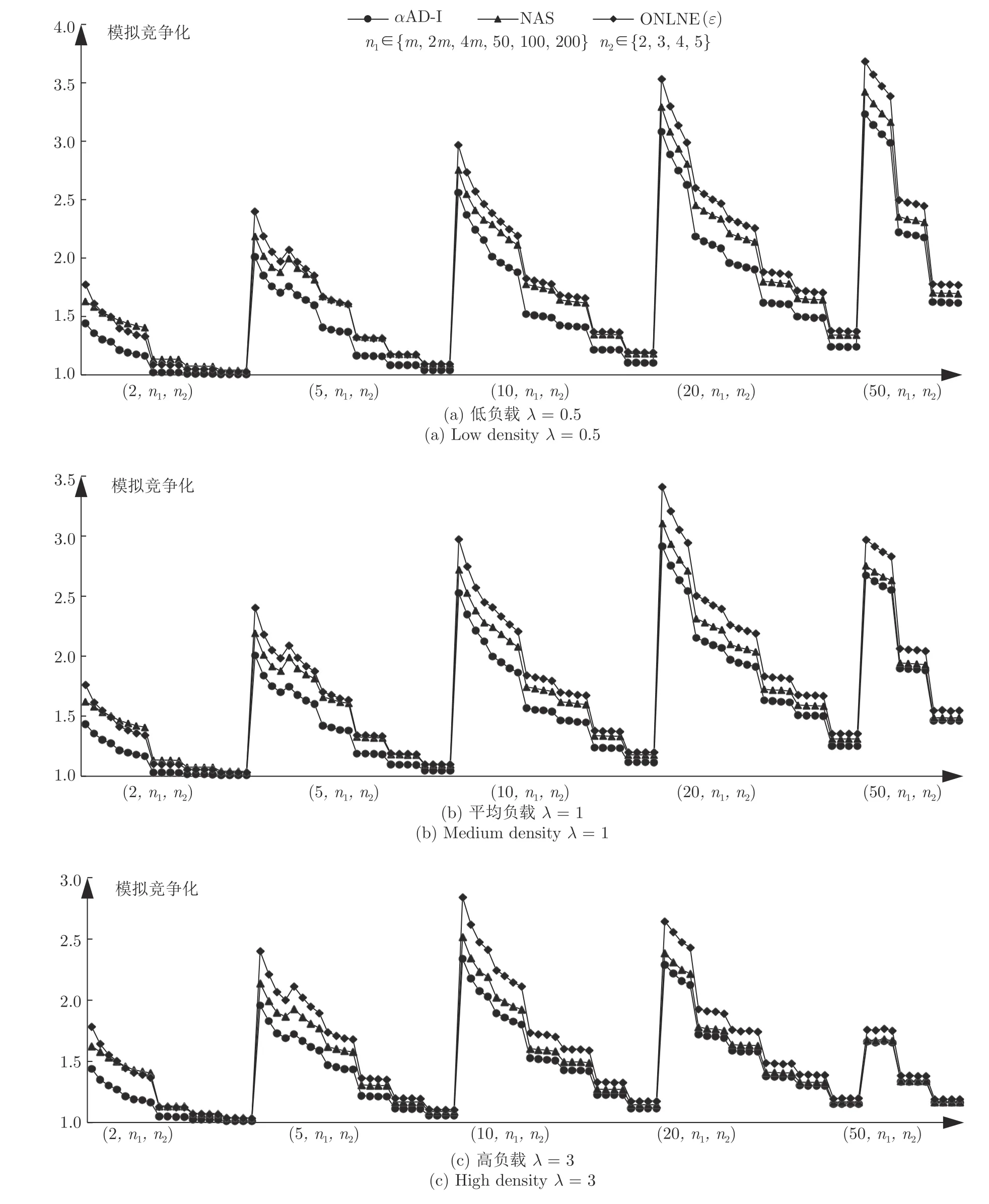
图6 α AD-I 算法在特殊实例 I* 下的实验结果Fig.6 The experimental results of α AD-I in I*

从图6 中可以看出,对不同的负载,均有特殊实例I*下αAD-I 算法的性能明显优于添加冲突机制后的NAS 算法以及 O NLINE(ε) 算法.且在m相同时,模拟竞争比随着n1、n2的增大而减小,算法性能与n1、n2呈正相关.

除此之外,横向对比,相同负载及相同n1、n2下,m增大到一定程度时,再继续增大,模拟竞争比不增反减,算法性能反而提高;纵向对比,相同m、n1、n2下,负载增大,模拟竞争比减小,算法性能提高.实验结果说明在特殊实例I*下,算法对大规模定制的市场环境具有良好的适应性,能够体现SPS的灵活性.

4.2 一般实例下 α AD-I 算法的性能检测

本节对一般实例下αAD-I 算法的性能进行检测,同样与添加冲突机制后的NAS 算法以及 ONLINE(ε)算法进行比较.

测试用例的生成与上小节类似,唯一的区别在于,对属于冲突集合F的Seru,处理时间从[1,100]中随机生成.同样对312 种不同的组合分别随机生成1 000 个测试用例,计算不同算法在每种组合下的模拟竞争比.

从图7 中可以看出,在一般实例下αAD-I 算法的性能也优于添加冲突机制后的NAS 算法以及ONLINE(ε) 算法.且具有和特殊实例I*下相似的实验结果.m相同时,算法性能与n1、n2呈正相关.横向对比,m增大到一定程度再继续增大,算法性能反而提高;纵向对比,负载增大,算法性能提高.实验结果同样说明在市场需求大幅度波动的情况下,算法具有良好的适应性,能够体现SPS 的灵活性.

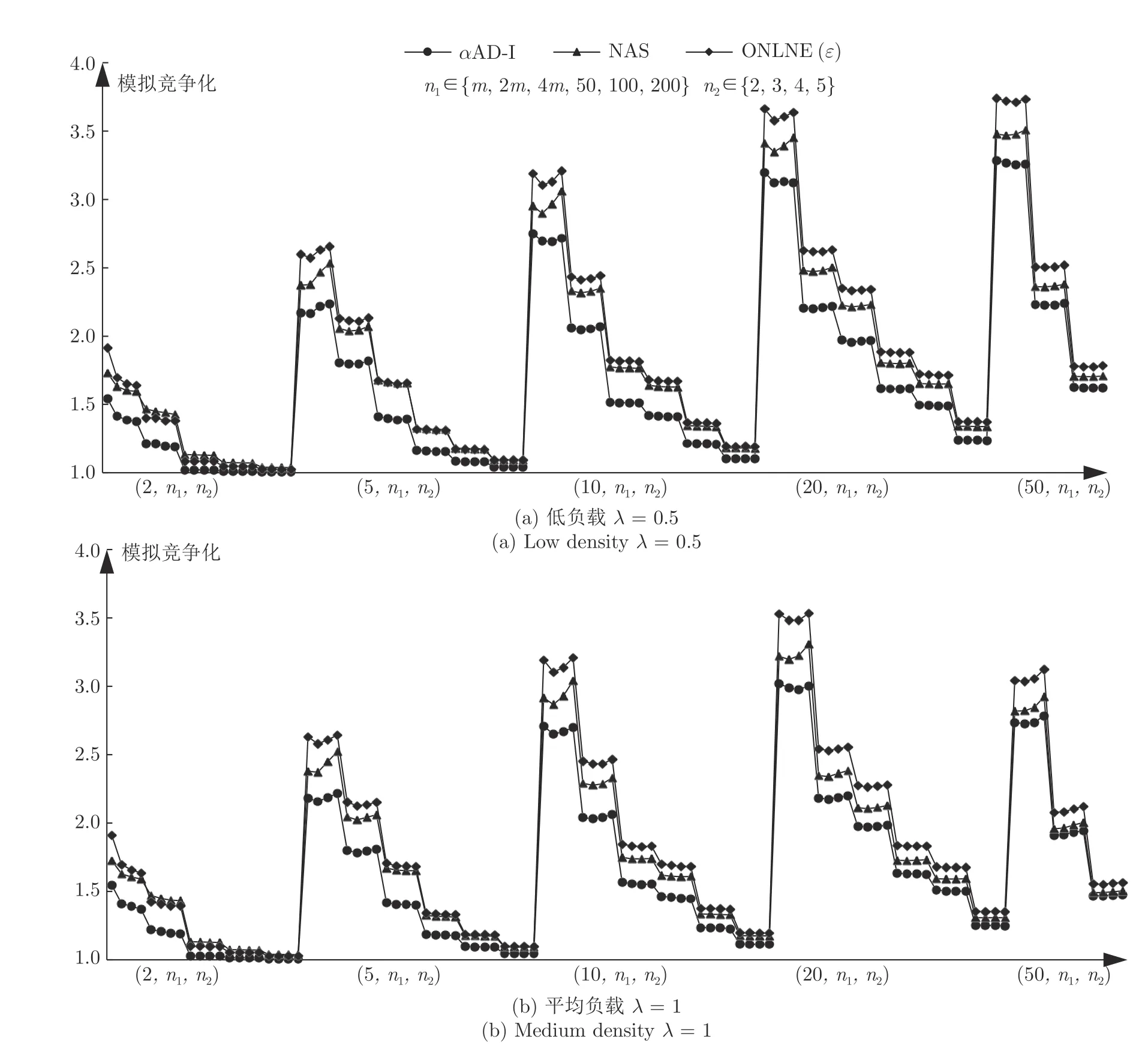
图7 α AD-I 算法在一般实例下的实验结果Fig.7 The experimental results of α AD-I in general instances

4.3 特殊实例 I* 与一般实例下的实验结果对比

在分别对特殊实例I*以及一般实例下αAD-I算法的性能进行检测后,再将两种情况进行对比.

图8 中展示了特殊实例I*与一般实例下αADI 算法模拟竞争比的对比,可以看出,相同负载下,在Seru的可用位置数目m相同时,随着n1、n2的增大,一般实例下的模拟竞争比与特殊实例I*之间的差距不断缩小直至可以忽略.且随着负载的增大,这种趋势的进程在不断加快.实验结果从一定程度上验证了,在大规模定制的市场环境中,一般实例下的αAD-I 算法同特殊实例I*下一样具有良好的性能.

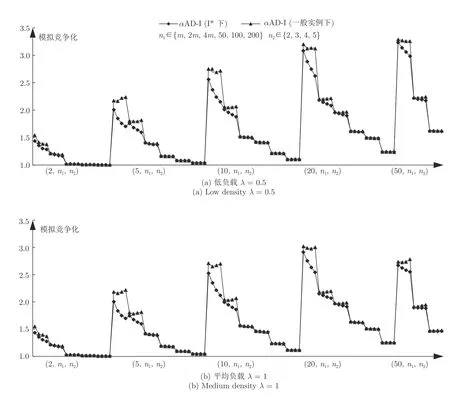
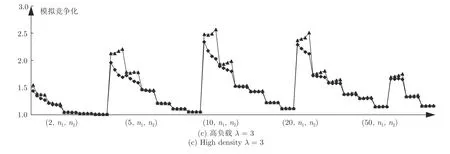
图8 α AD-I 算法在I*与一般实例下实验结果对比Fig.8 The comparision between α AD-I in I* and α AD-I in general instances

4.4 一般实例下 α AD-I 算法与AD-SWPT 改进算法的实验结果对比

根据第2.3.3 节的讨论,可知具有常数竞争比的αAD-SWPT 算法对比AD-SWPT 的改进算法不具有竞争比数值上的绝对优势,但是随着m的增大,二者竞争比间本就细微的差距在不断减小,因此在大规模定制的市场环境下这种微乎其微的差距可以忽略不计.

本节在一般实例下,对基于αAD-SWPT 算法的αAD-I 算法与添加冲突机制后的AD-SWPT 的改进算法进行计算机模拟实验,测试用例的生成同第4.2 节.

从图9 中可以看出,相同负载下,在m相同时,随着n1与n2的增大,αAD-I 算法的模拟竞争比较之添加冲突机制后的AD-SWPT 的改进算法,呈现从略大于到最后几乎相等的趋势,中间甚至有αAD-I 算法更加优越的情况出现.且随着负载和m的增大,这种趋势的进程在不断加快.λ=1,m=50 时,以及λ=3,m=20,50 时,两个算法的模拟竞争比曲线几乎完全重合.

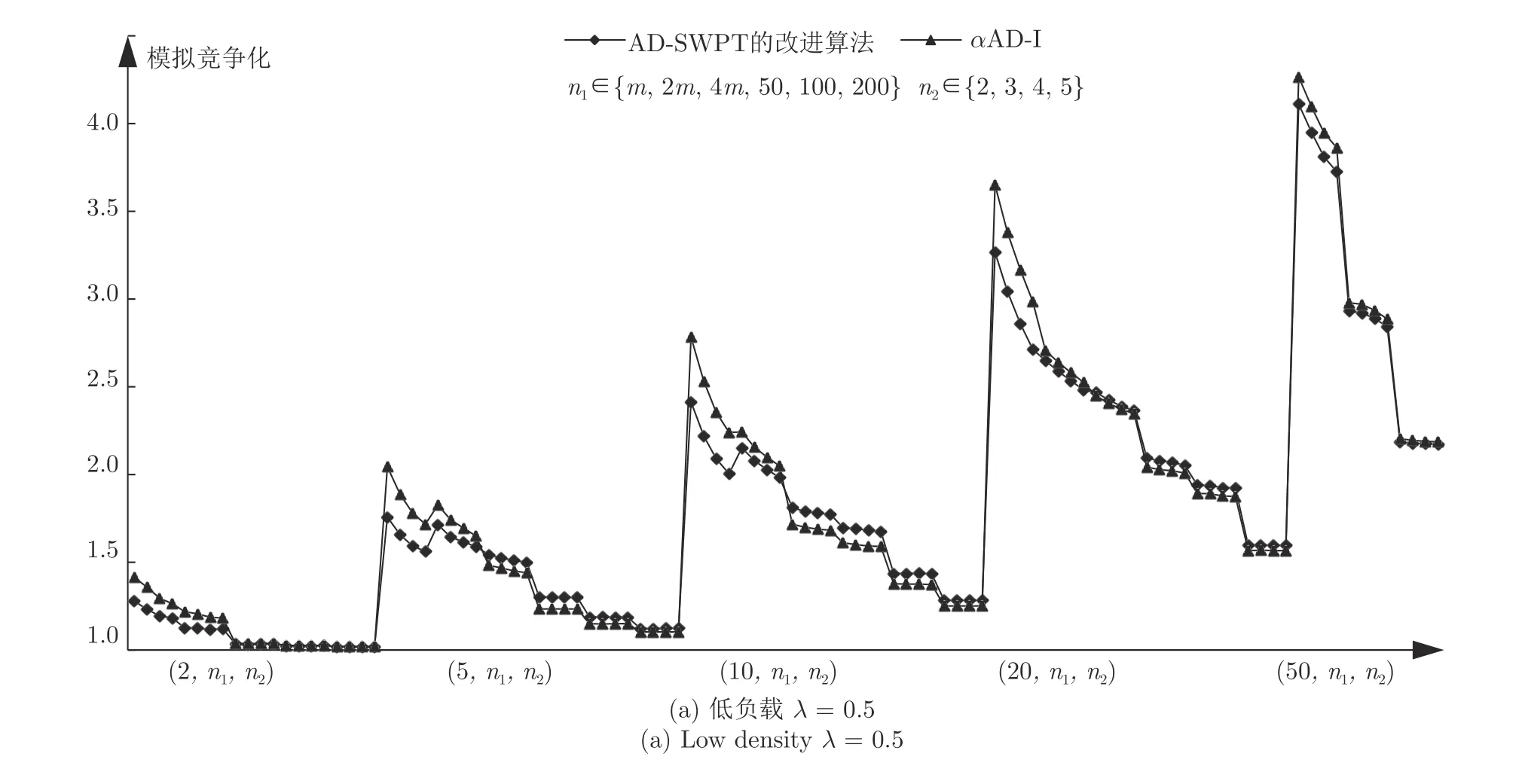
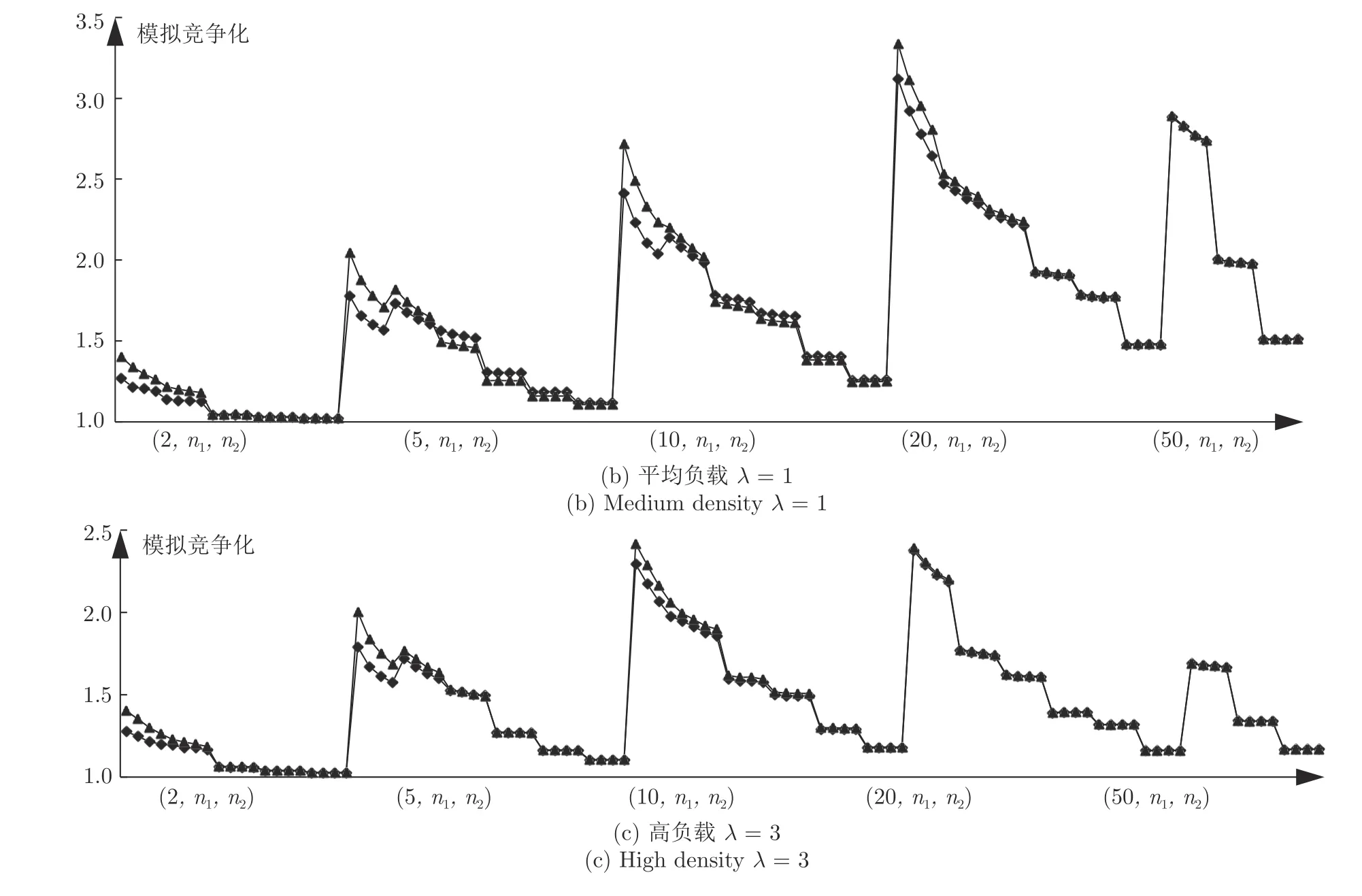
图9 α AD-I 算法与AD-SWPT 改进算法在一般实例下的实验结果对比Fig.9 The comparision between α AD-I and improved AD-SWPT in general instances

实验结果表明,在大规模定制的市场环境下可以忽略αAD-SWPT 算法在竞争比数值上的细微差距.为了推进算法竞争比的计算,在添加冲突机制时,选用具有常数竞争比的αAD-SWPT 算法是合理的.

5 结论

本文针对带有资源冲突的Seru在线并行调度问题,以总加权完工时间最小为目标,决策Seru的构建顺序及时间.先基于并行机在线调度问题的AD-SWPT 算法,针对无资源冲突的情况,采用实例归约的方法,引入调节参数α,得到竞争比为常数的αAD-SWPT 算法.

再针对有资源冲突的情况,基于αAD-SWPT算法添加冲突处理机制,得到带有资源冲突的Seru在线并行调度算法,即αAD-I 算法.沿用实例归约的方法,在特殊实例I*下可证明其竞争比同αADSWPT 算法,也为常数.

最后通过计算机模拟实验对αAD-I 算法的性能进行检测,对比添加冲突机制后的NAS 算法与ONLINE(ε) 算法,αAD-I 算法在特殊实例I*与一般实例下均具有更好的性能.且在市场需求大幅度波动的情况下,算法具有良好的适应性,能够发挥SPS 灵活的特点.且有,在大规模定制的市场环境中,一般实例与特殊实例I*下的αAD-I 算法均具有良好的性能.