胶辊式砻谷冲击振动隔离器力学特性研究

杨亚军，廖 敏，张 强，刘 鹏，向智宗

（1.西华大学 现代农业装备研究院，成都 610039； 2.四川省农业机械鉴定站，成都 610031）

随着国民生活质量的提高，鲜米机在国民生活中发挥越来越重要的作用，对其机械结构、技术指标提出了更加严格的要求。胶辊作为鲜米机的核心砻谷脱壳部件，也是鲜米机主要的振动来源[1]，砻谷过程中胶辊和谷粒之间的冲击振动会通过轴传递到机架，导致机架及其他部件发生振动，降低了鲜米机的可靠性、加工质量。为了减弱机械振动传递，常采用振动隔离装置对振动源本身进行控制[2]，通过弹性元件组成的隔离系统把振动源与机架的刚性连接变成弹性连接，提供一定缓冲力以减弱或阻断冲击振动的能量向机架传递，使系统在受到冲击力后的自由振动迅速衰减并趋于稳定，最终达到减振的目的[3]。

国内外学者在隔振器技术领域开展长期研究。针对半主动控制的磁流变阻尼器的隔振抗冲击技术进行了大量研究[4]，如汽车减振[5－7]、地震防护的设计[8－9]；应用于航空航天减振抗冲[10]。单树军等设计出一种可控阻尼的磁流体阻尼器[11]。张春辉等提出一种预紧式准零刚度隔离器[12]。高鹏等设计出一种纵、横向刚度一致的八连并联的隔离器[13]。目前隔离器结构适应于一定角度范围内的冲击隔离，而砻谷时的冲击振动特点为周向、高频率，还没有针对隔离鲜米机砻谷时产生冲击振动的隔离器或隔离系统，也没有对应冲击隔离技术的研究。

本文提出一种辊内六连杆隔离系统，该隔离系统由6 个预紧式隔离器对压并联构成，建立隔离系统的静力学模型，研究隔离系统的力学特性，给出了隔离系统刚度、平衡位置保持力的表达式，利用近似解析法建立运动学模型，采用傅里叶变换以及杜哈曼积分法求出了系统的响应表达式；分析了该隔离系统的力学特性，为设计该隔离系统提供理论支持。

1 隔离系统静力学分析

1.1 隔离系统关键机构

胶辊砻谷时产生的冲击为高频率、各向的瞬态冲击，而目前的半主动、主动的隔离系统需要一定的反应时间[14]，因此考虑被动式的隔离系统，隔离系统需要具有隔离各向冲击的能力，利用多连杆机构具有各向抗冲能力和变结构特性，提出一种辊内六连杆隔离系统，如图1所示，整个隔离系统分为内圈和外圈，六个隔离器对压并联组成弹性系统，弹性系统连接系统内圈与外圈，隔离器两两同首异尾地铰接安装在胶辊毂圈和轴盘之间，每个隔离器的首端安装在轴盘上，尾部铰接安装在胶辊毂圈上，使6个隔离器在初始位置3个铰接点形成正三角形。

图1 辊内六连杆隔离系统结构示意图

1.2 隔离系统静力学分析

1.2.1 铰点-轴心方向静力学分析

当胶辊所受冲击过铰点-轴心方向时，以隔离系统的轴心为原点，以轴心与铰点水平连线向右为正方向建立坐标系，隔离系统受到冲击力水平向右，则辊内六连杆隔离系统静态受力如图2所示。设铰点在受冲击时水平方向偏移x，隔离器在胶辊毂圈上均布的3个铰点到轴心的距离为R，初始位置时每个隔离器的两端铰接点的距离为L，每个隔离器中弹簧的预压缩量为E，每个弹簧的刚度为k，阻尼系数为c。

如图2所示，在进行静力学分析时，隔离器1 和6、2 和5、3 和4 的变形量一致，因此把隔离器1、6 合为I段，隔离器2、5合为Ⅱ段，隔离器3、4合为Ⅲ段，整个弹性系统由I、Ⅱ、Ⅲ并联组成，因此分别对I、Ⅱ、Ⅲ三段进行受力分析，再把三段的受力情况进行叠加，即可得到冲击过铰点-轴心方向时的整个隔离系统的受力情况。

图2 冲击在铰点-轴心方向时隔离系统静态受力简图

为了得到隔离器本身参数对隔离系统的特性影响，分段对隔离系统中的隔离器进行数学建模。

（1）对I段：

对于隔离器1、6铰点-轴心方向（所受冲击方向）的夹角θ1为：

当胶辊在水平正方向偏移x时，隔离器1、6的变形量△L1为：

则隔离器1、6产生水平方向弹力的合力F1为：

把隔离系统的等效刚度用微分刚度来表示，即公式（3）对x求导，得到隔离器1、6 在水平方向的等效刚度K1为：

（2）对Ⅱ段：

对于隔离器2、5铰点-轴心方向（所受冲击方向）的夹角θ2为：

当胶辊在水平正方向偏移x时，隔离器2、5的变形量△L2为：

则隔离器2、5产生水平方向弹力的合力F2为：

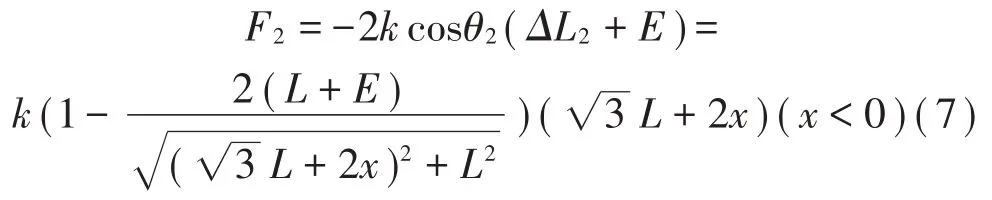
从公式（7）中得出I段隔离器1、6 的弹力与Ⅱ段隔离器2、5 的弹力在水平方向分力相反。公式（7）对x求导，得到隔离器2、5 在水平方向的等效刚度K2为：

当设于隔离器中的弹簧被拉伸时，弹簧提供阻尼力给铰接在底座的隔离杆，当弹簧被压缩时，隔离杆受弹簧提供的弹力；由图1中的坐标系方向可知，当冲击力为x正向时，隔离器1、6 中的弹簧受到压缩，为隔离系统提供弹力；当冲击力为x负向时，隔离器2、5中的弹簧受到压缩，为隔离系统提供弹力；当冲击力为水平方向时，隔离器3、4都被拉伸，不提供弹力给隔离系统，因此冲击力过铰点-轴心方向时隔离系统静态偏移的合力和等效刚度分别为：

令：偏移比xc=x/L，预压缩比e=E/L，无量纲合力Fc=F/(Lk)，无量纲总刚度Kc=K/k，由式（9）、式（10）得到式（11）、式（12）：

由于F=kLFc，其中k和L都为常数项，因此Fc的变化可以表示隔离系统静态偏移合力F的变化，利用MATLAB对式（11）绘制不同的e值下Fc随xc变化的特性曲线，得到隔离系统合力-偏移比的特性曲线图，如图3所示，得出曲线为关于原点中心对称且成跳跃型曲线，说明xc和e相同时，得到的隔离系统合力大小相同；随着e增大，隔离系统的合力越大，隔离系统在初始位置越稳定，因此可以通过调节弹簧的预压缩量，隔离系统得到不同的初值压力；在e相同时，曲线的切线斜率近似水平，即x大小对隔离系统合力影响不大，影响隔离系统的稳定性主要是e。

图3 隔离系统无量纲合力-偏移比的特性曲线图

由于K=kKc，弹簧刚度k为常数，因此隔离系统的K变化可以由Kc的变化来代表，通过对式（12）绘制不同e下隔离系统Kc随xc的变化曲线，如图4所示，在相同xc情况下，随着e变小，隔离系统Kc增大。

由图4可得xc对系统刚度影响较大，但实际胶辊的偏移量x远小于隔离器的两端铰接点的距离L，因此把xc缩小两个数量级，得到隔离系统在实际偏移量下无量纲刚度变化曲线，如图5所示。

图4 隔离系统无量纲刚度-偏移比的特性曲线

由图5中可得，每条曲线近似直线，说明在实际xc的情况下，xc对隔离系统的刚度影响很小；随着e的变化，隔离系统的刚度变化较大，进一步说明影响隔离系统的稳定性主要因素是e。

图5 隔离系统无量纲刚度-实际偏移比的特性曲线

1.2.2 胶辊圆周静力学分析

辊内六连杆隔离系统中的隔离器为正三角布局，因此只要讨论任意相邻两铰点-轴心60°夹角内胶辊受力情况。冲击力在非铰点-轴心方向时隔离系统的受力如图6所示，轴心-铰点的连线为水平方向，其冲击力与过轴心的水平线夹角为β（0°≤β＜60°），由于轴盘是固定的，因此只有系统外圈的铰点才发生偏移，且只有隔离器的弹簧受到压缩时才提供弹力，因此在F作用下，只有隔离器1、3、6中的弹簧受到压缩提供弹力。

图6 冲击力在非铰点-轴心方向时隔离系统的受力简图

由图6分析可知隔离系统在0°≤β＜60°的区间内圆周法向上的保持力的合力为：

由式（13）可得隔离系统在水平铰点-轴心方向上（β=0°）的保持力为：

采用非铰点-轴心方向与水平铰点-轴心保持力的比值来体现非铰点-轴心方向保持力的特性，则比值为：

对式（15）绘制不同夹角β情况下保持力比值g的变化曲线，如图7所示，保持力在0°≤β<60°范围内关于β=30°直线对称，在β=30°时取得最大值为2 3 /3，在β=0°、60°时取得最小值为1，表示保持力在铰点-轴心方向最小；通过上述分析结果，绘制出隔离系统在整个圆周上保持力比值g的变化曲线，如图8所示。

图7 保持力比值的变化趋势图

图8 隔离系统周向保持力比值变化图

隔离系统的保持力最小值出现在铰点-轴心方向，而保持力在非铰点-轴心较大，且保持力关于原点中心对称，因此只需保证铰点-轴心方向的保持力大小，则整个隔离系统的稳定性就可以得到保证，由式（9）至式（12）得到隔离系统在初始平衡位置（偏移量x=0）铰点-轴心的保持力与总刚度为：

2 隔离器动力学分析

2.1 隔离器动力学方程建立

由1.2.1可知预压缩比e是影响隔离系统稳定性的主要原因，且无量纲刚度特性曲线近似直线，因此把隔离系统的刚度视为初始平衡位置刚度K=(3-e)k/2。设隔离系统等效总阻尼系数为C，每个隔离器的阻尼系数均为c，胶辊偏移量为x，胶辊偏移速度为，胶辊偏移加速度为，则总阻尼力Fd为：

把偏移比xc=x/L代入公式（18）化解后得到：

由1.2.1可知，实际偏移比xc远小于1，则隔离系统等效总阻尼系数C可化简为：

对隔离系统采用近似解析法求解，设：胶辊质量为M，F′(t)表示激励力克服等效保持力F0后的系统等效激励力，则隔离系统的简化运动微分方程为：

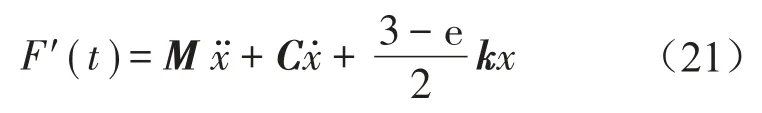
2.2 求解脉冲激励力

对式（21）中F′(t)求其对应的傅里叶系数，得出F′(t)的傅里叶展开式，用F′(t)的傅里叶函数合成单向周期脉冲激励力F(t)，则式（21）对应的傅里叶系数展开式表达式为：

式中：j-1,2,3,…,n。

当激励力没有克服保持力F0时，由式（22）得到单向周期脉冲激励力F(t)为：

对式（23）绘制F(t)关于时间t的曲线，添加基本参数：A=340 N，ωp=209 rad/s，tp=0.002 s，Tp=0.03s，如图9所示。

图9 单向周期脉冲激励力-时间变化曲线

2.3 位移响应

采用杜哈曼积分对非周期内的任意时间的脉冲进行求解，每次脉冲大小为I，F(t) 为连续的脉冲激励函数，初时刻时，隔离系统受到时间为dτ的单次脉冲作用，则冲量I=F(t) ∙dτ作用于质量M的弹性系统，质量M产生初速度0；根据振动理论，当带阻尼弹簧的线性系统在弱阻尼情况下初始偏移量x0为0，可得到单次脉冲激励；根据在扰力F(t) 由τ=0到τ=t的连续作用下，隔离系统的总响应为τ=t时刻之前的所有单次脉冲激励叠加，则隔离总响应为：

根据胶辊的尺寸以及设计的隔离器模型参数，设定：弹簧刚度k=15 N/mm，阻力系数c=0.088 N/(mm∙s-1)，胶辊质量M=5 kg，F(τ)=F(t)；得到胶辊在周期脉冲作用于辊内六连杆隔离系统时的位移响应曲线，如图10所示。

图10 位移响应曲线图

由图可知，隔离系统响应快速趋于稳定，响应的脉冲频率与脉冲激励力频率一致，位移响应在平衡位置（x=0）跳动，且偏移量x在（-0.09 mm～0.29 mm）之间，最大偏移量为0.29 mm。

3 结语

（1）随着预压缩比e逐渐增大，系统的无量纲合力-偏移比的特性曲线图中的零点阶跃量越大，表明随着隔离器中的弹簧预压缩量的增加，整个隔离系统更加稳定，则隔离系统在平衡位置的初值压力可以通过选择不同的弹簧的预压缩量进行调节。

（2）在实际偏移比xc很小的情况下，隔离系统在平衡位置的稳定性主要影响因素是预压缩比e，隔离系统在平衡位置的无量纲刚度随预压缩比e越大而减小。因此可以通过选择不同的预压缩比e使隔离系统的刚度在实际行程范围内随偏移比xc变化而变化，当有较大的异物进入到砻谷区时，可以有效地保护隔离系统、传动系统。

（3）隔离系统圆周上的保持力关于原点中心对称，保持力的最小值出现在铰点-轴心方向，因此只需要保证铰点-轴心方向的保持力大小，则整个隔离系统的初值压力、稳定性都可以得到保证。

（4）隔离系统的响应频率与脉冲激励频率一致，隔离系统的偏移量x在（-0.09 mm～0.29 mm）之间，最大偏移量为0.29 mm。