基于CFD和风洞试验的钢桁梁悬索桥颤振稳定性分析
2022-03-09蓝先林周礼平徐向东朱承前
蓝先林,周礼平,廖 斌,何 淼,徐向东,朱承前
(1.贵州省交通规划勘察设计研究院股份有限公司,贵阳550081;2.中铁武汉勘察设计研究院有限公司,武汉430074)
随着“交通强国”等战略的提出,我国西南地区桥梁建设得到迅猛发展。悬索桥是一种刚度小且主要由主缆受力的柔性体系桥梁,常用于山区峡谷沟壑地区。这类地区风环境复杂,风产生的颤振对悬索桥的破坏将是毁灭性的[1]。因此,十分有必要对复杂山区的悬索桥颤振稳定性进行专题研究。
桥梁颤振问题是一种发散问题,桥梁结构是否发生颤振,主要与主梁断面形式、悬索桥关键频率和风环境有关[2]。国内外学者主要用风洞试验[3]和CFD(Computational fluid dynamics)数值模拟[4]两种方法对桥梁振动控制[5-7]进行研究。徐洪涛等[8]基于某千米级大跨度钢桁梁悬索桥主梁节段模型试验,得到了与桥梁颤振稳定性有关的三分力系数和8个颤振导数,并从理论和经验两方面评价了该钢桁梁悬索桥的颤振稳定性能。董佳慧等[9]基于稳定板、导流板、风嘴等气动优化措施,结合节段模型试验,研究了某悬索桥的颤振稳定性。熊龙等[10]先后利用CFD 数值模拟和风洞试验,研究了某钢桁梁悬索桥颤振性能和气动优化措施。Thai 等[11]、Wang 等[12]和Zhu 等[13]等研究了多塔悬索桥颤振性能,詹昊等[14]、Boberg 等[15]和Bakis 等[16]等基于流固耦合和气动导数计算了悬索桥的颤振临界风速。上述学者仅探究了平原和海峡地区悬索桥的颤振稳定性问题,而对复杂山区的钢桁梁悬索桥颤振问题研究较少。
基于上述研究,以山区某钢桁梁悬索桥为研究背景,结合CFD 数值模拟和风洞试验,从气动导数和流固耦合两方面探究复杂山区风环境作用下钢桁梁悬索桥颤振稳定性问题,可为同类桥梁抗风设计提供参考。
1 基本参数确定
1.1 工程背景
以贵州省某超大跨度钢桁梁双塔悬索桥为研究背景,探究复杂山区超大跨钢桁梁悬索桥颤振稳定性研究。该桥主跨为1 100 m,主缆边跨分别为302 m、123 m。加劲梁采用板桁结合加劲梁,加劲梁标准断面宽为B=27.0 m,桁架高为H=7.2 m。主缆采用抗拉强度为1 860 MPa 的高强度镀锌铝合金钢丝,共173股,每股由91根直径为5.30 mm的钢丝组成。桥塔采用混凝土桥塔,主塔塔高分别为135 m、139 m。
1.2 风参数的确定
根据设计资料可知,本桥距贵阳市大约60 km~80 km,参考贵阳市基本风速来确定本桥桥位基本风速。据文献[17]可知,在平坦开阔条件下,贵阳市10 m高度、100年重现期、10分钟平均时距年最大风速(即桥位基本风速)为:
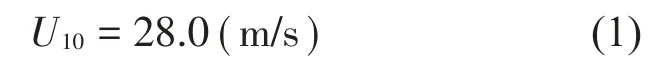
本桥桥位处于峡谷地区,对应的地表类别为D类地表,风剖面指数α0=0.30。桥梁设计基本风速为:

式中:kc表示基本风速地表类别转换系数,对于D类地表取0.564。
桥面基准高度为:

式中:Zh表示桥面距水面的高度。
加劲梁跨中基准高度为162.95 m,则对应加劲梁设计基准风速可按下式计算:

式中:kf为抗风风险系数,取为1.02。
成桥状态-5°~+5°风攻角下桥梁颤振稳定性按下式检验:

式中:Uf表示颤振临界风速;Ud表示桥面高度设计基准风速;γf为颤振稳定性分项系数,采用风洞试验方法获取颤振临界风速时取1.15,采用CFD 方法获取颤振临界风速时取1.25;γt为风速脉动修正系数,该悬索桥桥主跨为1 100 m,桥位地表为D 类地表,故对应的风速脉动修正系数取γt=1.32;γα为攻角效应分项系数,当风攻角α为0°、±3°时取1.0,当风攻角α为±5°时,取0.7。
据式(5)可得到该桥风洞试验和数值模拟的成桥态桥梁颤振检验风速如表1所示。
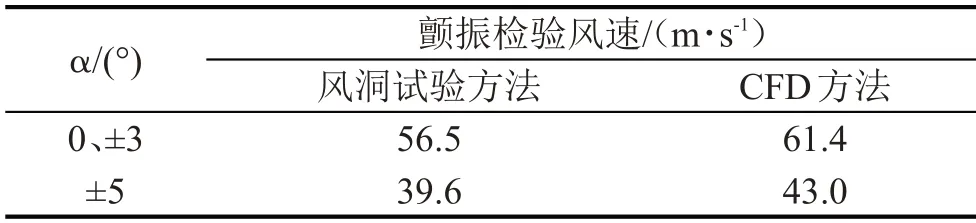
表1 成桥状态桥梁颤振检验风速
1.3 动力特性参数
基于软件ANSYS建立全桥有限元模型,并结合实际支座布置情况设置模型约束条件,其约束情况如表2所示。

表2 约束情况
板桁结合加劲梁主桁杆件采用空间梁单元(BEAM189)模拟,桥面板采用空间壳单元(SHELL63)模拟,主缆、吊杆、中央扣均采用空间杆单 元(LINK10)模拟,桥塔采用空间梁单元(BEAM189)模拟,其有限元模型如图1所示。

图1 有限元模型
采用Block Lanczos 法计算结构动力特性,得到与抗风性能研究有关的关键频率和振型如表3所示。

表3 关键频率和振型
2 数值模拟
2.1 颤振临界风速计算
根据CFD 识别的气动导数对成桥状态结构振型形状相似的扭弯振型组合进行二维颤振临界风速分析,得到颤振临界结果,并将结果与流固耦合计算结果对比,进而确定颤振临界风速。
(1)主梁断面气动导数计算
气动导数是表征桥梁主梁断面气动自激力的重要气动参数,其与结构断面运动状态线性组合表示气动力的线性部分。根据Scanlan 自激力气动力模型可知,主梁断面气动自激力表达式为:

式中:ρ为空气密度;K为折算频率,K=2πfB/U;H*i、A*i为薄平板断面的气动导数,i为1~4;h和B分别为截面高度和宽度。
采用分状态单自由度强迫振动的方式计算薄平板断面在不同振幅的气动自激力,其中风攻角α 分别为0°、±3°与±5°,风速U分别为2 m/s、4 m/s、6 m/s、8 m/s与10 m/s,扭转运动振幅取为2.0°,竖向运动振幅分别取为3.0 cm,振动频率f均为2.0 Hz。CFD计算模型仍采用静三分力计算的网格,并设置动网格区域。
根据桥梁加劲梁断面气动自激力时程,采用最小二乘法识别薄平板断面气动导数。限于篇幅,此处仅给出不同风攻角下的桥梁加劲梁断面的气动导数A*1和A*2随折算风速的变化曲线如图2所示。

图2 气动导数随折算风速的变化曲线
根据CFD 识别的气动导数对成桥状态结构振型形状相似的扭弯振型组合进行二维颤振临界风速分析,得到颤振临界结果如表4所示。

表4 气动导数计算的颤振临界风速/(m∙s-1)
(2)流固耦合数值计算
流固耦合是采用CFD 进行桥梁断面的自由振动计算,可直接得到桥梁断面的颤振位移响应。几何缩尺比为λL=1:50,风速比为λV=1:5,动力参数选取扭转频率较低的正对称振型组合。
选取0°、+3°与+5°风攻角进行流固耦合计算,得到不同风速下时程响应曲线,如图3所示。由图3可知,0°风攻角下,实桥风速U为55.0 m/s时,振幅剧烈发散;+3°风攻角下,实桥风速U为45.0 m/s时,振幅剧烈发散;实桥风速U为35.0 m/s 时,振幅剧烈发散。

图3 位移时程曲线
(3)颤振临界风速对比
根据CFD 识别的气动导数对成桥状态结构振型形状相似的扭弯振型组合进行二维颤振临界风速分析,得到颤振临界风速结果,并将结果与流固耦合计算结果对比,流固耦合计算结果见表5。

表5 流固耦合计算的颤振临界风速/(m∙s-1)
由表4和表5可知,风攻角为0°与+3°时,流固耦合计算结果与气动导数计算的颤振临界风速较为一致;风攻角为+5°时,流固耦合计算结果与气动导数计算的颤振临界风速差异较大,气动导数计算的颤振临界风速结果大于流固耦合结果。
2.2 主梁断面颤振性能优化
根据2.1节计算结果可知,原始加劲梁断面颤振稳定性不满足规范要求,需要进行气动优化。研究表明,设置中央稳定板对提高桁架加劲梁悬索桥的颤振临界风速有明显作用,故采用中央稳定板方案对该桥进行气动优化,具体主梁断面气动性能CFD数值模拟优化所采用的气动措施汇总如表6所示。

表6 气动措施优化方案
其中H1和H2分别为上、下稳定板高度,分别使用气动导数和流固耦合两种方法对表6中所有方案进行计算。颤振临界风速近似值计算结果如表7所示。

表7 不同方案下颤振临界风速/(m∙s-1)
通过5 种优化方案的综合比较可知,方案1(H1=1.2 m 的上稳定板)与方案5(H1=1.4 m 的上稳定板)效果总体较好,表明上稳定板效果优于下稳定板。考虑到桁架加劲梁为典型的三维结构,二维CFD数值模拟方法计算结果仅供参考,后续桥梁颤振稳定性将通过主梁节段模型风洞试验来进行进一步检验,并将重点针对上稳定板方案进行研究。
3 风洞试验
3.1 节段模型
第2节从数值模拟的角度探究了复杂山区大跨度钢桁梁颤振稳定性,该桥处于复杂的山区风环境下,且跨度达到千米级,有必要通过风洞试验对其颤振稳定性进行研究。
3.2 节段模型试验参数
加劲梁节段模型试验参数如表8所示。由表8可以看出,加劲梁节段模型尺寸、质量、质量惯性矩及频率均与设计值误差较小,弹性悬挂系统竖向振动阻尼比为ξh=0.44%,扭转振动阻尼比为ξa=0.42%,均小于规范值(0.5%)。
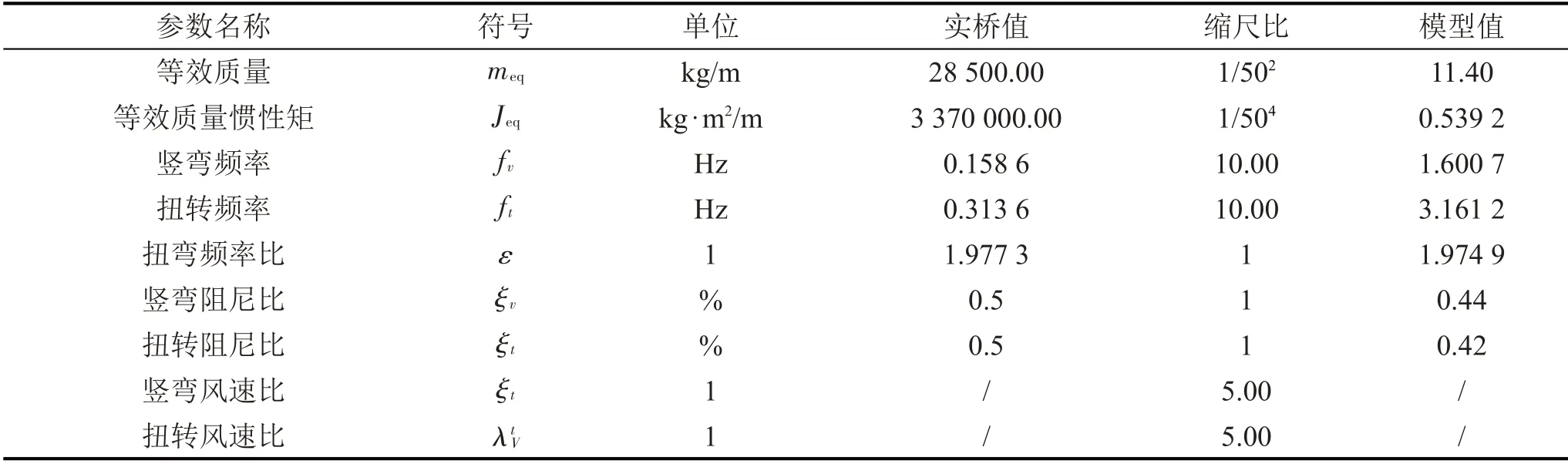
表8 加劲梁节段模型测振试验参数

图4 加劲梁节段模型
3.3 试验工况
首先针对原始断面加劲梁节段模型,进行风攻角为0o、±3o和±5o时加劲梁节段模型测振试验。其次,为提高颤振稳定性,采用1.2 m 上中央稳定板气动优化方案,进行风攻角为0o、±3o和±5o时加劲梁节段模型测振试验。所有试验工况均在均匀流场下进行,针对原始断面和1.2 m上中央稳定板优化后的断面均进行0o、±3o和±5o风攻角的风洞试验,共计10个试验工况。
3.4 颤振稳定性试验结果
限于篇幅,此处仅给出竖向振动和扭转振动位移响应,如图5所示。
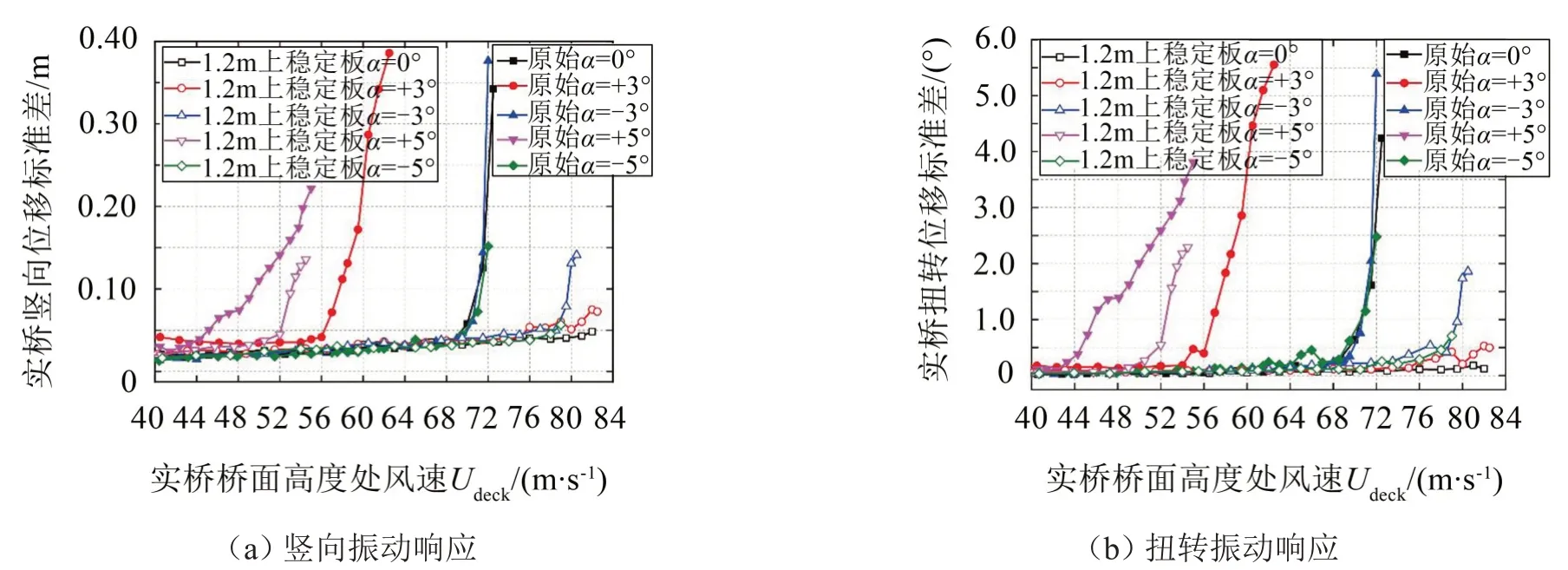
图5 颤振位移响应
成桥状态加劲梁颤振临界风速如图6所示。分析图6可知,原始断面0°风攻角下颤振临界风速为68.5 m/s;在0°、-3°与±5°风攻角下,颤振临界风速大于颤振检验风速,在+3°风攻角颤振临界风速小于颤振检验风速,颤振稳定性不满足规范要求;采用1.2 m上中央稳定板优化后,颤振临界风速显著提高,0°风攻角下颤振临界风速为82.0 m/s;0°、±3°与±5°风攻角下,颤振临界风速均大于颤振检验风速,颤振稳定性满足规范要求。
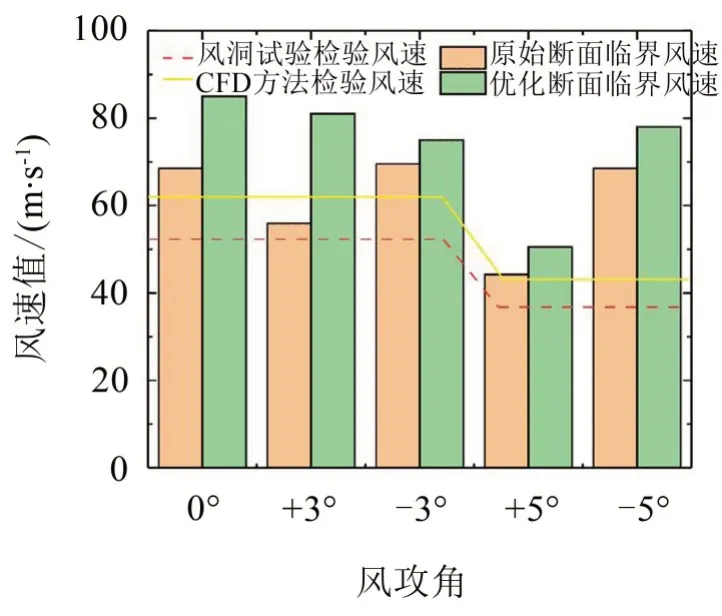
图6 临界颤振风速
4 数值仿真与风洞试验对比
在数值仿真和风洞试验下的原始断面和采用1.2 m 上中央稳定板气动优化方案的颤振临界风速见表9,分析表9可知。

表9 数值仿真与风洞试验结果对比
(1)数值模拟和风洞试验得到的原始断面颤振临界风速均要小于优化断面颤振临界风速;
(2)数值模拟得到的颤振临界风速要小于风洞试验得到的颤振临界风速。有可能是因为数值模拟在利用气动导数和流固耦合方法识别颤振临界风速时具有一定的人为主观性,为避免该类问题的发生,应编制相关颤振临界风速识别程序,这也是后续要研究的工作。
5 结语
基于CFD 数值模拟和风洞试验探究了复杂山区超大跨钢桁梁悬索桥颤振稳定性,主要结论如下:
(1)桥位基本风速U10=28.0 m/s,桥位处地表类别为D 类,对应的地表粗糙度系数为α0=0.30;对应的成桥状态加劲梁设计基准风速Ud=37.20 m/s。
(2)风攻角为0°、+3°与+5°时,原始断面颤振临界风速小于颤振检验风速,不满足规范要求。
(3)设置上中央稳定板可以明显提高颤振临界风速,0°风攻角颤振临界风速大于70.0 m/s,大于颤振检验风速;风攻角为+3°与+5°时,1.2 m 上稳定板的颤振临界风速分别为52.3 m/s 与37.3 m/s,1.4 m上稳定板颤振临界风速分别为56.0 m/s与47.0 m/s。
(4)风洞试验结果表明:主梁原断面在0°、-3°与±5°风攻角下,颤振临界风速大于颤振检验风速;在+3°风攻角颤振临界风速小于颤振检验风速,不满足规范要求;增设H1=1.2 m上中央稳定板后,各试验攻角下主桥结构颤振临界风速均大于该桥颤振检验风速,颤振稳定性满足规范要求。
