基于深度学习的微电网优化调度辅助决策方法
2022-03-08陈卫东吴宁黄彦璐马溪原郭晓斌林冬
陈卫东,吴宁,黄彦璐,马溪原,郭晓斌,林冬
(1. 广西电网有限责任公司电力科学研究院,南宁530013;2. 南方电网数字电网研究院,广州510663)
0 引言
微电网技术作为一种提高分布式电源消纳、多能源互补利用、以及提高供电可靠性的关键解决方案,已在南方电网范围内加快推广,在解决无电岛、偏远山区供电等方面应用潜力巨大,是南方电网公司“能源价值链整合商”转型的重要组成部分[1 - 2]。
微电网的优化调度是保证微电网安全、可靠、经济运行的重要手段,是微电网相关研究的热点问题[3 - 4]。传统的微电网优化调度通常基于最优化的理论和方法,首先对微电网内部各元件进行建模,然后对模型进行简化和处理,最后研究相应的求解算法对模型进行求解。模型的目标函数一般为运行成本最小,也有相关研究综合考虑经济、环境以及社会效益建立多目标优化模型[5 - 6];常用的模型建模方法包括混合整数规划[7 - 8]、动态规划[9]、模型预测控制[10]、分布式优化[11]、李雅普诺夫优化[12]等;常用的模型求解算法包括遗传算法[13]、粒子群算法[14]、主动进化算法[15]、拉格朗日松弛法[16]等。近年来,随着风机、光伏等可再生能源的高比例接入,微电网的运行不确定性显著加大,如何应对不确定性因素成为微电网优化调度的难点问题。此类问题常用的解决办法是将不确定性问题转换成确定性问题进行建模求解,主要包括基于场景的随机优化[17 - 18]、机会约束优化[19]、鲁棒优化[20 - 21]等,但这些方法均存在一定的局限性,如随机优化计算量较大、鲁棒优化过于保守等,而且微电网系统运行不确定因素较为复杂时,其概率建模较为困难。
目前,微电网正逐步演变为具有开放性、不确定性和复杂性的新型系统,强间歇性可再生能源高比例接入、高渗透率电力电子装备、多能源耦合等新模式对微电网的物理特性及运行控制产生重要影响,上述传统模型驱动的建模求解方法已难以满足需求,主要体现在:
1)微电网各元件的精细化建模较为困难,简化模型难以描述元件实际运行的物理特性,导致优化结果可能是次优的;
2)所建立的模型一般是非线性非凸的,其本身求解是典型的非确定性多项式难题(non-deterministic polynomial hard,NP-hard),求解效率较低;
3)模型的建立需要依据拓扑结构和运行方式完成,对拓扑结构的变化以及新型电力设备接入的适应性不强;
4)基于“离线计算、在线匹配”的预案式控制难以适应复杂多变的系统工况。
5)不能充分利用所积累的历史决策数据信息。
此外,南方电网公司正在向“能源价值链整合商”转型,将有可能运维数以万计的微电网,传统的基于人工值守的调度模式将难以适应这种新形态和新业态的出现。人工智能是新一轮科技革命和产业变革的重要驱动力量,研究其在系统调度运行的应用有助于突破传统解决方案的局限性。目前,深度学习等机器学习算法在系统优化调度中的应用主要集中在负荷预测方面,直接应用在系统调度决策的相关研究较少[22 - 25]。文献[26]基于长短期记忆网络,构建了面向机组组合问题的深度学习模型,通过历史数据的训练建立系统负荷与调度决策之间的映射关系,并以此进行机组组合决策,但所构建的网络结构较为简单,且缺乏对模型输出结果的处理,导致调度决策很可能不满足运行过程中复杂的约束关系。
面向人工智能在微电网自动运行调控领域的需求,针对传统模型驱动、预案式控制、人工值守调度模式和方法的缺陷,本文提出基于深度学习的微电网自动运行调控模型和方法,该方法基于深度双向长短期记忆网络(bidirectional long-short term memory, Bi-LSTM),通过历史运行数据的训练,直接构建微电网系统运行场景与调度决策结果之间的映射关系,并提出模型输出结果的处理原则,可实现微电网功率的快速平衡与经济优化,该方法可以作为物理优化模型方法的辅助决策方法,解决了传统微电网运行优化调控模型求解效率低、难以适应复杂多变运行工况等难点问题,提升了微电网调度运行的智能化程度。
1 微电网日前优化调度典型数学规划模型
1.1 目标函数
微电网日前优化调度的目标是一天内系统的总运行成本最低。系统的总运行成本包括微型燃气轮机等可控分布式发电机组的燃料成本和启动成本、储能电池的充放电成本以及微电网与大电网之间的购售电成本,具体可表示为:
(1)
(2)
式中:T为调度周期;N为可控机组的数量;CFuel,i,t和CSU,i,t分别为可控机组i在时段t的燃料成本和启动成本;CES,t为储能电池在时段t的充放电成本;CGrid,t为微电网与大电网在时段t的购售电成本;ai、bi、ci为可控机组i的燃料成本系数;SUi为可控机组i的启动成本;KES为储能电池的单位充放电成本;pt为电网在时段t的电价;PG,i,t为可控机组i在时段t的出力;Pcha,t和Pdis,t分别为储能电池在时段t的充电功率和放电功率;PGrid,t为微电网与大电网在时段t的交换功率,其中,PGrid,t>0表示微电网从大电网买电,反之为微电网向大电网卖电;non,i,t和nsu,i,t分别为指示机组运行和启动状态的二进制变量,non,i,t=1表示可控机组i在时段t处于运行状态,反之non,i,t=0;nsu,i,t=1为可控机组i在时段t启动,反之nsu,i,t=0。ηcha、ηdis分别为储能电池的充电效率和放电效率。
1.2 约束条件
微电网日前优化调度模型的约束条件包括系统功率平衡约束、可控机组运行约束、储能电池运行约束、微电网与大电网间联络线的功率约束等等,具体可表示如下。
1.2.1 系统功率平衡约束
微电网优化调度必须保证系统功率实时平衡,如式(3)所示。
(3)
式中:PLoad,t为系统在时段t的负荷;PWT,t和PPV,t分别为风机和光伏在时段t的预测出力。等式右侧为系统的净负荷,表征微电网的运行工况,等式左侧变量为微电网日前优化调度的决策变量。
1.2.2 可控机组运行约束
可控机组运行约束包括可控机组的出力约束、爬坡约束、最小运行时间和停运时间约束以及机组的状态指示变量约束等,如式(4)—(12)所示。
PG,i,min·non,i,t≤PG,i,t≤PG,i,max, ∀i,t
(4)
-Pi,RD≤PG,i,t-PG,i,t-1≤Pi,RU, ∀i,t
(5)
nsu,i,t-nsd,i,t=non,i,t-non,i,t-1, ∀i,t
(6)
nsu,i,t+nsd,i,t≤1, ∀i,t
(7)
UTi=min{T,(Ton,i-Ion,i)·non,i,0}
(8)
DTi=min{T,(Toff,i-Ioff,i)·(1-non,i,0)}
(9)
non,i,t=non,i,0,t≤UTi+DTi,∀i
(10)
(11)
(12)
式中:PG,i,min和PG,i,max分别为可控机组i的最小出力和最大出力;Pi,RD和Pi,RU分别为可控机组i的最大下调出力和最大上调出力;nsd,i,t为指示机组停运状态的二进制变量,nsd,i,t=1表示可控机组i在时段t停运,反之nsd,i,t=0;UTi为0时刻初始状态为运行状态时的持续时间,DTi为0时刻初始状态为停机状态时的持续时间;Ton,i和Toff,i分别为可控机组i的最小运行时间和最小停运时间;Ion,i和Ioff,i分别为可控机组i的初始运行时间和初始停运时间;non,i,0为可控机组i在0时刻的运行状态。
1.2.3 储能电池运行约束
储能电池运行约束包括储能电池的充放电状态约束、充放电功率约束、储能电池容量约束、调度周期内储能平衡约束等等,如式(13)—(18)所示。
ncha,t+ndis,t≤1, ∀t
(13)
0≤Pcha,t≤Pcha,max·ncha,t, ∀t
(14)
0≤Pdis,t≤Pdis,max·ndis,t, ∀t
(15)
EES,t=EES,t-1+Pcha,t·ηcha-Pdis,t/ηdis, ∀t
(16)
Ec·socmin≤EES,t≤Ec·socmax, ∀t
(17)
(18)
式中:ncha,t和ndis,t为指示储能电池充放电状态的二进制变量,ncha,t=1表示储能电池在时段t充电,反之non,i,t=0;ndis,t=1表示储能电池在时段t放电,反之nsu,i,t=0;Pcha,max和Pdis,max分别为储能变流器的最大充放电功率;EES,t为储能电池在时段t的容量;Ec为储能电池的最大容量;socmax和socmin分别为储能电池的最大、最小荷电状态。
1.2.4 联络线功率约束
-PGrid,max≤PGrid,t≤PGrid,max, ∀t
(19)
式中PGrid,max为微电网与大电网联络线允许交换的最大功率。
上述模型是一个混合整数非线性规划模型,求解效率相对较低。为了提高模型的求解效率,需要对微电网内各元件的精细化数学模型进行简化处理,使得模型的求解精度下降,进而导致所优化出来的结果可能是次优的,甚至是不可行的。此外,模型驱动的微电网调度决策方法忽视了历史调度决策结果对未来调度决策结果的指导意义,模型和算法一旦确定,针对任一场景的微电网优化调度问题,其求解精度和计算效率都不会改变。
2 微电网日前优化调度的深度学习模型
针对模型驱动的微电网优化调度模型的技术难点与缺陷,本文提出一种基于深度Bi-LSTM的微电网日前优化调度辅助决策方法,该方法通过海量历史数据的训练,直接构建微电网运行场景与决策结果之间的映射关系,可实现微电网日前功率的快速平衡与辅助决策。
2.1 Bi-LSTM神经网络的基本结构单元
长短期记忆网络LSTM由瑞士人工智能科学家Jürgen Schmidhuber在1997年提出[27],是一种特殊的循环神经网络,广泛应用于序列预测、自然语言处理等任务中。
LSTM通过新增记忆单元,同时引入输入门、遗忘门和输出门等门控单元控制信息的遗忘与刷新,可有效解决循环神经网络在长序列训练过程中出现的梯度弥散和梯度爆炸问题,适用于处理时间序列较长的数据信息,其基本结构单元如图1所示。

图1 LSTM的基本结构单元
LSTM基本结构单元的前向传播过程如式(20)—(25)所示。
gf=σ(Wf[ht-1,xt]+bf)
(20)
gi=σ(Wi[ht-1,xt]+bi)
(21)
go=σ(Wo[ht-1,xt]+bo)
(22)
(23)
(24)
yt=ht=go∘ tanh(ct)
(25)

由LSTM的基本结构单元可见,在每个时间戳t,LSTM只能提取当前输入和过去时间序列的特征信息,忽略了未来时间序列的特征信息。而Bi-LSTM在隐层同一时间戳同时包含一个正向LSTM和一个反向LSTM,并且二者都连接着一个输出层,这样的结构提供给输出层输入序列每一个时间戳完整的过去和未来的上下文特征信息,在丰富模型表达能力的同时,并没有增加对数据量的要求。Bi-LSTM的基本结构单元如图2所示。

图2 Bi-LSTM的基本结构单元
微电网系统负荷预测数据以及调度决策信息是典型的具有时间先后顺序的序列数据,且微电网日前优化调度周期较长,采用擅长处理较长时间序列数据的LSTM进行输入输出映射关系的学习较为合适。此外,微电网日前优化调度决策需要满足可控机组爬坡约束(5)、最小运行和停运时间约束(11)—(12)、储能电池容量与充放电功率关系约束(16)等时间耦合约束,使得微电网当前时段的调度决策结果受过去和未来时段风机出力、光伏出力以及负荷的运行工况的影响。因此,选择Bi-LSTM神经网络构建微电网日前优化调度的深度学习模型更能有效提取微电网运行工况的特征信息,进而可以更准确地描述微电网运行场景与调度决策结果之间的映射关系。
2.2 基于深度Bi-LSTM神经网络的微电网日前优化调度辅助决策方法
基于深度Bi-LSTM神经网络的微电网日前优化调度模型通过海量历史数据的训练,构建微电网运行场景与调度决策结果之间的映射关系,进而针对风电、光伏、负荷任一场景的日前预测数据即可直接映射出相应的调度决策结果,具体网络模型和详细的决策流程如图3所示。

图3 网络模型和决策流程示意图
由图3可见,微电网日前优化调度的深度学习模型由双层Bi-LSTM神经网络构成,其中,第1层Bi-LSTM的输出作为第2层Bi-LSTM神经网络的输入;整体模型的输入为日前24时段的系统净负荷,可由日前24时段风机、光伏以及负荷的预测数据得出;整体模型的输出为日前24时段的调度决策结果,具体包括每台可控机组各时段的出力大小、储能电池各时段的充放电功率以及微电网与大电网联络线的交换功率。
在进行网络训练之前,需要将训练样本数据进行归一化处理。具体地,系统净负荷数据以及可控机组出力数据归一化到[0,1]之间,储能电池的充放电功率以及微电网与大电网联络线的交换功率归一化到[-1,1]之间,如式(26)—(31)所示。
Pnet,t=PLoad,t-PWT,t-PPV,t
(26)
Pes,t=Pdis,t-Pcha,t
(27)
(28)
(29)
(30)
(31)
式中:Pnet,t为系统在时段t的净负荷;Pes,t为储能电池在时段t的充放电功率,Pes,t>0表示放电,反之表示充电;Pnet,t0、PG,i,t0、Pes,t0、PGrid,t0分别为系统净负荷、可控机组出力、储能充放电功率以及微电网与大电网联络线交换功率的归一化值。
本文采用Adam优化算法[28]来进行双层Bi-LSTM神经网络的训练,选取均方误差(mean squared error, MSE)作为损失函数,MSE的表达式以及Adam算法的权重更新公式如式(32)—(35)所示。
(32)
(33)
(34)
(35)

值得注意的是,基于深度学习的微电网日前优化调度辅助决策方法不研究优化调度的内在机理,所输出的调度决策结果很可能不满足微电网系统功率平衡约束以及各元件的运行约束等,因此,需要对网络输出的结果进行相应处理,具体的处理原则如下。
1)若模型输出的可控机组出力小于0.5倍最小技术出力,则认为可控机组出力为0;若模型输出的可控机组出力在0.5倍最小技术出力与最小技术出力之间,则认为可控机组出力为最小技术出力;
2)若模型输出的可控机组出力、储能充放电功率以及联络线交换功率数值超过上限,则输出值取为上限;
3)若模型输出的可控机组相邻两个时段的出力不满足机组上下爬坡约束,则可控机组下一时段的出力等于上一时段的出力加上(减去)最大上调(下调)出力;
4)若模型输出的可控机组各时段运行状态不满足最小运行和停运时间约束,则未满足最小运行(停运)时间的时段,可控机组出力为最小技术出力(0);
5)若模型输出的储能电池各时段运行容量不满足容量约束,则不满足容量约束的时段根据最大(小)荷电状态确定储能的充(放)电功率;
6)储能电池调度周期最后一个时段的充放电功率数值取决于调度周期其他所有时段充放电功率的总和,以满足调度周期内储能平衡约束;
7)微电网与大电网联络线各时段的交换功率取决于当前时段系统净负荷、可控机组出力以及储能充放电功率,以满足系统功率平衡约束。
应按照原则的先后顺序依次对网络的输出结果进行处理:先处理不等式约束,后处理等式约束;先处理元件约束,后处理系统约束。
此外,由图3可见,本文微电网日前优化调度深度学习模型的训练是随着时间推移持续进行的,通过历史输入数据与输出数据的积累可以实现对深度学习模型的持续修正,进而可以有效计及历史调度决策结果对未来调度决策的指导意义,不断提高微电网日前优化调度的求解精度与效率。因此,本文基于深度学习的微电网日前优化调度方法可以很好地作为模型驱动方法的辅助与备用。
3 算例分析
3.1 算例参数设置及测试系统描述
为了验证本文所提方法的有效性,选取一个典型的并网型微电网系统进行仿真测试,并将测试结果与基于混合整数规划的模型驱动的调度决策结果进行对比分析。该并网型微电网系统包含1台风力发电机组、1台光伏发电机组、储能电池系统以及4台微型燃气轮机发电机组。其中,风机和光伏的装机容量均为800 kW,储能电池容量为3 600 kWh,初始电池容量为1 500 kWh,变流器最大充放电功率为500 kW,最大、最小荷电状态分别为0.95和0.15,充放电效率设为0.95,单位充放电成本为0.08 元/kWh,4台微型燃气轮机发电机组的技术成本参数如表1所示,该系统与大电网联络线交换的最大功率为1 000 kW,日前交易的分时电价如图4所示。

表1 微型燃气轮机技术成本参数

图4 日前分时交易电价
本文基于Python 3.7的Tensorflow 2.0 深度学习框架完成基于深度Bi-LSTM神经网络的微电网日前优化调度模型的构建、训练与评估。网络离线训练所需的输入数据为风机、光伏和负荷的日前预测数据,来源于欧洲开放的电力系统数据平台OPSD[29],输出标签数据为基于混合整数规划的模型驱动的调度决策结果,包括日前24时段的4台微型燃气轮机机组的出力、储能充放电功率以及与电网交换的功率。选取500个训练样本进行深度Bi-LSTM神经网络的训练和测试,其中前450个训练样本作为训练集,后50个训练样本作为测试集,如图5所示。为减少神经网络参数的数量,第1层Bi-LSTM的输入为微电网系统的净负荷,张量形状为(24,1),第1层Bi-LSTM的输出与第2层Bi-LSTM的输入相同,张量形状为(24,64),第2层Bi-LSTM的输出为调度决策结果,张量形状为(24,6),所建立的深度Bi-LSTM神经网络需要训练的总参数数量为37 200个,离线训练的学习率设为0.01。
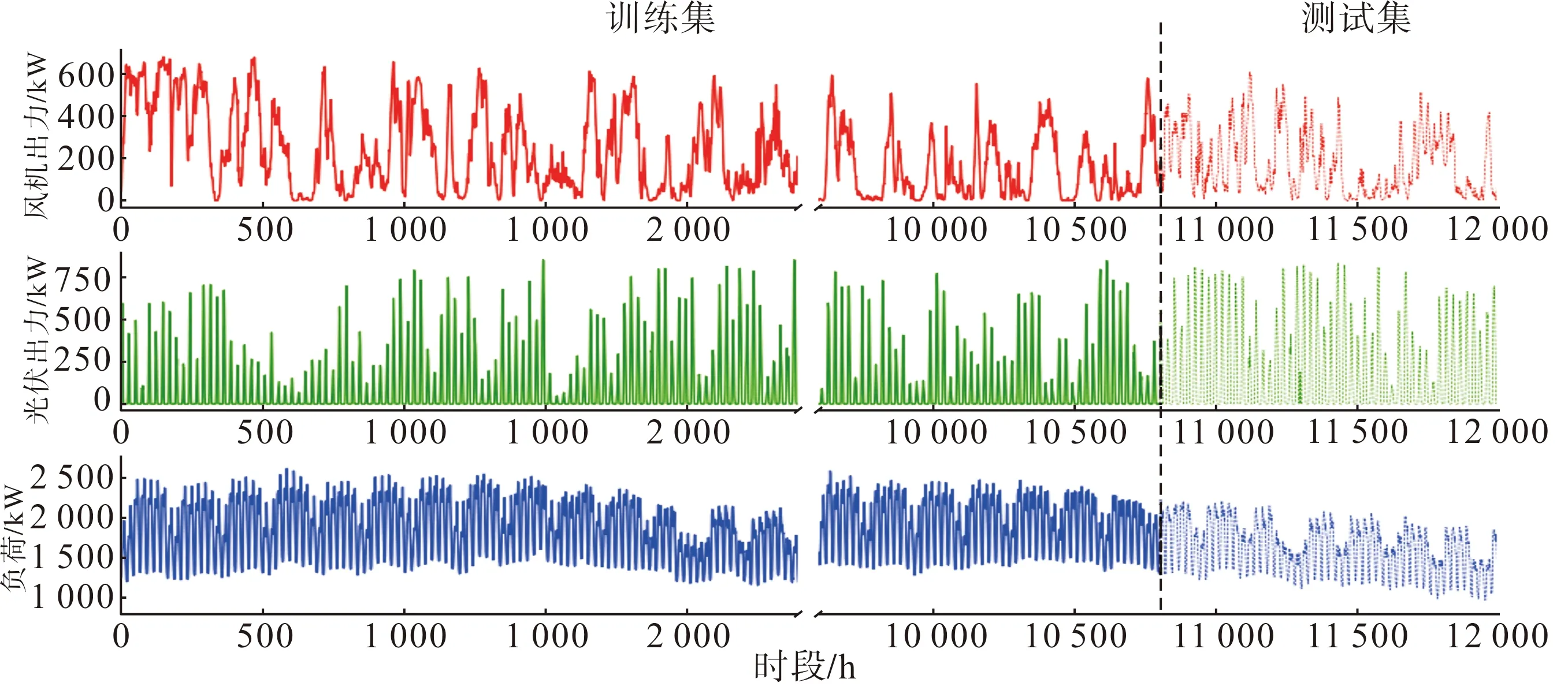
图5 训练集与测试集数据
微电网日前优化调度的混合整数规划模型使用GAMS 24.4调用CPLEX 12.0求解器进行求解,算法相对间隙设为1%,上述仿真测试均在处理器为Intel Core i5- 1035G4 CPU @ 1.10 GHz, 1 498 MHz,内存为16 GB的环境下进行。
3.2 算法有效性分析
首先,将上述训练集再次切分为训练集和验证集,选取前400个样本作为训练集用于训练深度学习模型参数,后50个样本作为验证集用于在训练过程中选择合适的模型超参数,并判断模型是否过拟合。其中,回合大小(Epoch)为500、批量大小(Batch)为10的深度Bi-LSTM模型的训练过程如图6所示。

图6 网络模型的训练过程
由图5可见,在训练了500个回合之后,模型接近于收敛,训练误差低于0.005,训练准确率达到了0.8,此时验证误差为0.01,验证准确率为0.83,训练误差和验证误差都很低,训练准确率和验证准确率接近,说明所训练好的网络模型并没有出现欠拟合或者过拟合的现象。另外,在训练200个回合之后,验证误差基本不再下降,验证准确率不再上升,可以认为此时模型达到了最佳状态,可提前终止网络模型的训练。
利用训练好的网络模型结合测试集中50个场景的风机、光伏以及负荷的预测数据进行微电网日前优化调度决策,并采用本文第2节中网络输出结果的处理方法对调度优化结果进行修正,即可得出测试集50个场景的基于深度学习的微电网优化调度决策结果。其中,前2个场景的微电网优化调度决策结果如图7所示。
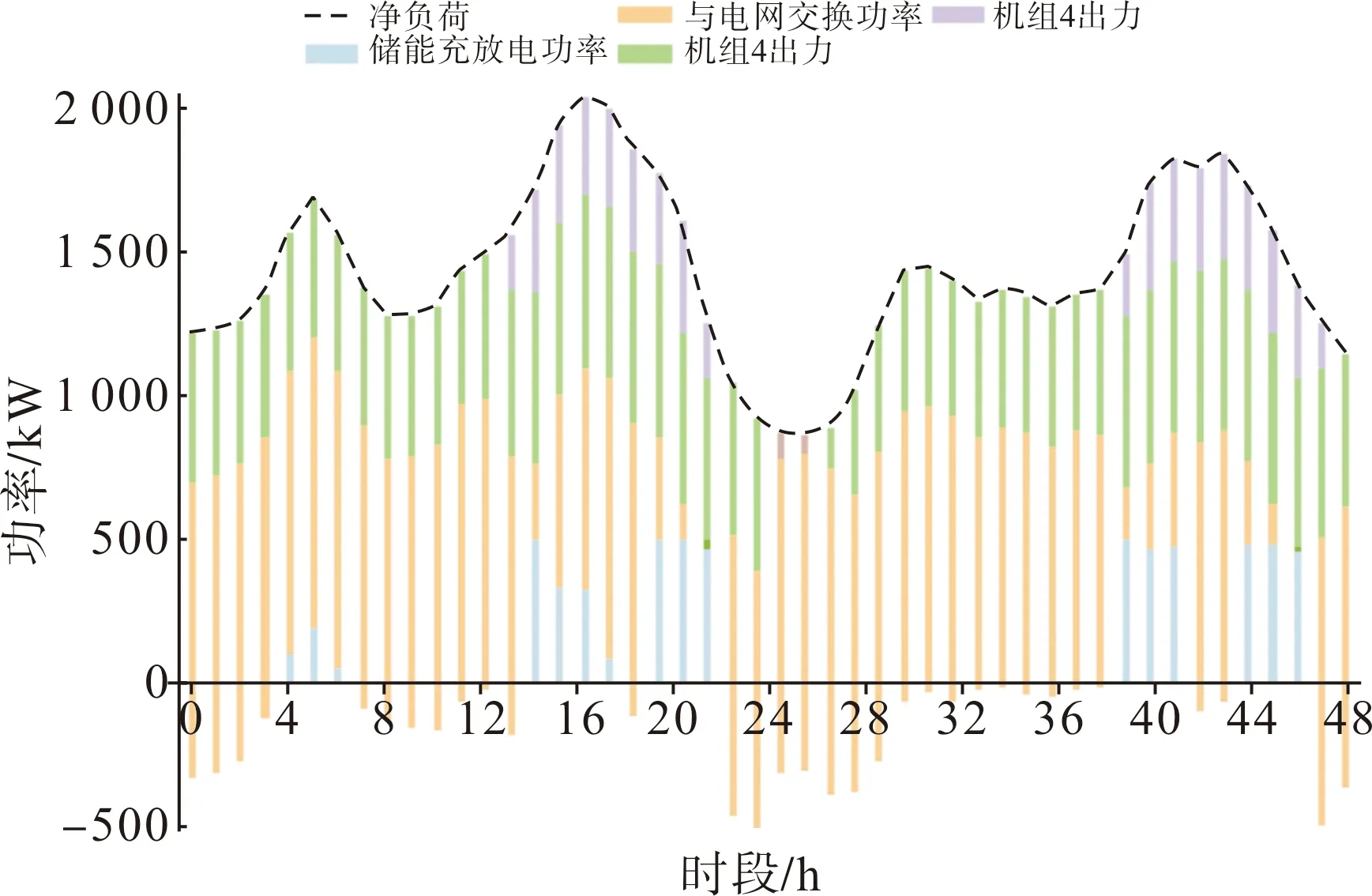
图7 基于深度学习的微电网日前优化调度决策结果
由图7可见,基于深度学习的微电网日前优化调度模型可直接根据风机、光伏、负荷的日前预测数据映射出微电网的日前优化调度结果,其决策时间十分短,可实现微电网系统功率的快速平衡。另外,采用本文方法得出的调度决策结果较为合理,具体表现在:1)储能电池在系统净负荷低谷时充电,在系统净负荷高峰时放电;2)在电网峰时电价时段(时段21和时段46),微电网向大电网售电;3)运行成本最低、启动成本最高的机组4在大部分时段保持运行状态,不频繁启动,运行成本和启动成本相对较低的机组2在系统净负荷高峰时启动以维持微电网系统的功率平衡。
为了进一步验证本文方法的有效性和准确性,将基于本文方法与基于混合整数规划模型以及基于深度置信网络[25]得出的调度决策结果进行对比,测试集前10个场景的计算决策时间和系统总运行成本的对比结果分别如表2和图8所示。
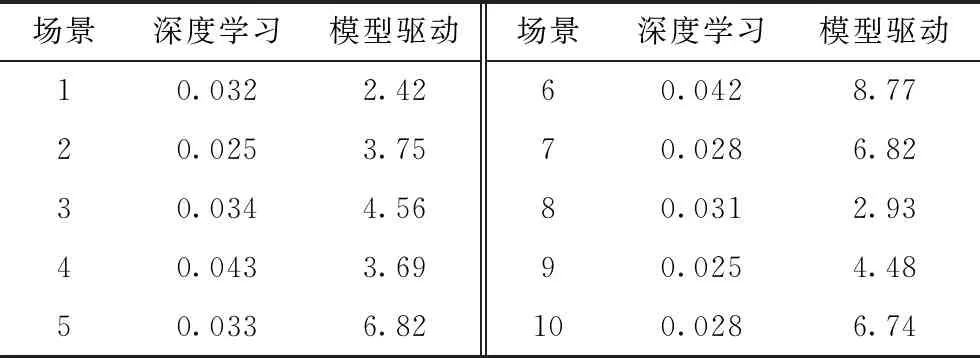
表2 3种方法计算时间的对比结果

图8 3种方法系统总运行成本的对比结果
由表2可见,深度学习方法的计算求解时间远低于模型驱动方法,且深度学习方法的计算结果是通过输入输出的映射关系得到的,不会随着模型复杂度的增大导致计算求解时间大幅上升。此外,由图8可见,由于在日前优化调度中,本文将模型驱动算法的计算结果作为训练目标样本进行深度Bi-LSTM神经网络的训练,使得本文方法得出的系统总运行成本略高于模型驱动方法优化出的系统总运行成本,但结果十分接近,平均误差仅为1.42%,而基于深度置信网络方法得出的系统总运行成本平均误差为4.84%,可以验证本文方法的有效性和准确性。
3.3 算法结果对比分析
首先分析不同的训练样本容量对于基于深度学习的微电网优化调度决策结果的影响,分别对比训练样本容量为50、100、150、200、250、300、350、400时深度学习模型和混合整数规划模型在测试集的性能表现,测试集前10个场景的总运行成本以及测试准确率的对比结果如图9所示。

图9 不同训练样本容量的对比结果
由图9可见,基于混合整数规划模型驱动的调度决策结果与训练样本的容量无关,即历史决策结果对未来决策结果没有指导意义,一旦模型和算法确定,其计算效率和求解精度均不会改变。而深度学习模型的决策精度会随着训练样本容量的增加而提高,在训练样本容量为50时,深度学习模型计算出的总运行成本为243 540.23元,与最优运行成本的相对误差为3.35%,测试准确率为0.754 2;而当训练样本容量增加到400时,深度学习模型计算出的总运行成本为235 798.89元,与最优运行成本的相对误差仅为0.07%,测试准确率提高至0.868 3。因此,深度学习模型可以计及历史决策结果对未来决策结果的影响,在历史数据不断积累的过程中不断对模型进行修正训练,进而不断提高模型的决策精度。
图10对比了采用7种不同的神经网络结构和类型训练100个回合的训练过程。可见,单层单向LSTM训练的收敛过程较慢,双层单向LSTM和3层单向LSTM训练过程的波动性较大,较不稳定,而相比于单向LSTM,采用双向LSTM训练的收敛过程更快,同时也更稳定,双层双向LSTM与3层双向LSTM的训练效果类似,根据奥卡姆剃刀原理,选用双层双向LSTM构建基于深度学习的微电网日前优化调度模型最为合适。

图10 不同网络结构和类型的对比结果
最后,分析不确定性对该微电网系统实时在线优化调度决策结果的影响,不确定性的来源为系统内风机、光伏以及负荷的日前预测误差。图11对比了不同的预测误差下分别采用本文算法和采用模型驱动算法进行调度决策平均运行成本。其中,本文算法在离线阶段训练好深度神经网络并直接应用于在线决策;模型驱动算法在离线阶段得到系统的预调度结果,实时的不平衡量通过考虑各元件的上下调裕度和成本进行再调度从而消除。由图11可见,随着预测误差的增大,即不确定性的增大,本文算法的优势逐渐增大,当预测误差达到20%时,本文算法相对于模型驱动的算法平均运行成本下降了6.2%。这是由于本文算法基于大量的样本进行训练,训练样本的分布能够自适应不确定性的变化;而模型驱动的算法由于难以对复杂的不确定性进行建模从而导致实时再调度成本的增加,证明了本文算法应对不确定性的效果更好。
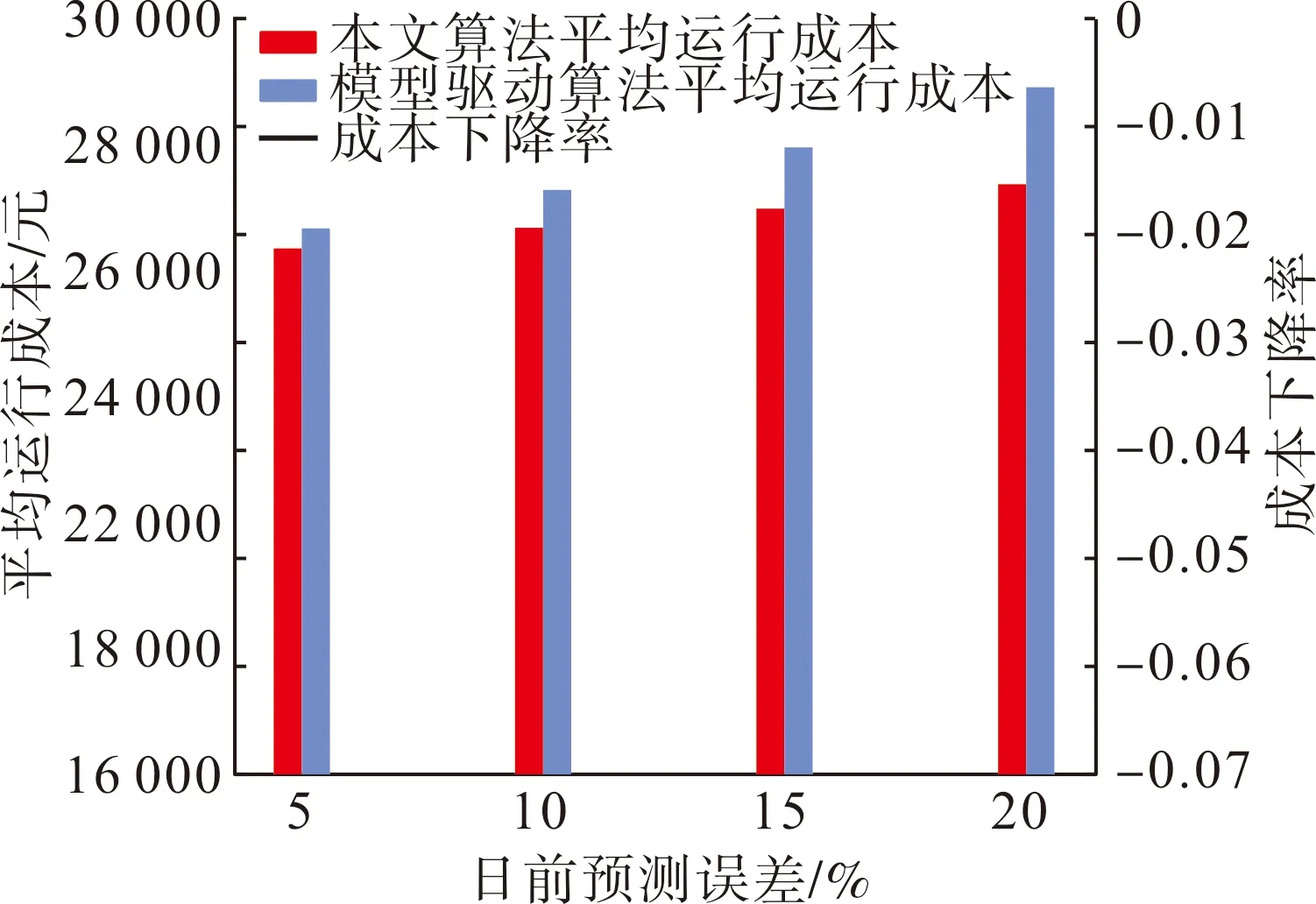
图11 不同预测误差下两种算法平均运行成本的对比结果
4 结论
针对模型驱动的微电网优化调度方法的局限性,本文提出了一种基于深度学习的数据驱动的微电网日前优化调度模型和辅助决策方法,通过算例分析,可得出以下结论。
1)基于深度Bi-LSTM神经网络构建了微电网日前优化调度的深度学习模型,可以直接学习微电网运行场景与调度决策之间的映射关系,实现微电网日前功率的快速平衡与辅助决策;
2)提出了深度学习模型输出结果的处理原则,可以有效解决调度决策结果可能不满足系统硬性运行约束条件的问题;
3)基于深度学习的微电网日期优化调度模型可以充分利用历史调度决策信息,通过历史数据的积累,对模型持续地进行修正和训练,进而不断提高模型的求解精度。
