基于解析Preisach模型的非晶合金磁滞特性模拟

余蓓，李晓露

(上海电力大学电气工程学院，上海200090)

0 引言

非晶合金凭借其低矫顽力、高磁导率、低损耗等优点，近年来已被广泛应用于高频变压器等高频电力设备中[1 - 2]。在非晶合金的应用中，其固有的磁滞特性会对变压器的励磁电流、能量损耗等产生重要影响[3 - 4]，因而如何准确、高效模拟非晶合金的磁滞特性具有重要意义。

目前，国内外学者对非晶合金的磁滞特性研究主要通过实验测量的方式，而鲜有设计相关理论和模型对其进行准确模拟。例如，文献[5]为了探究非晶合金的损耗机理，通过实验直接测量了大量磁滞回线，进而对其形状、矫顽力、剩磁等特性进行分析。文献[6]直接在实测非晶合金磁滞特性曲线的基础上，进行数值分解，从而提出了一种双曲模型模拟非晶合金磁畴壁移动、磁畴旋转等磁化过程。现有已被提出模拟磁性材料磁滞特性的磁滞模型有Jile-Atherton(J-A)[7 - 9]、Preisach[10 - 13]模型等。其中，J-A模型是一种基于磁性材料内在能量守恒的物理模型，由于其在推导过程中存在多处近似处理，导致其模拟精度较低。Preisach模型是一种基于宏观磁滞现象的数学模型，求解精度较高，但参数辨识需要大量实验数据，且实现过程较为复杂、耗时。由于非晶合金的磁滞回线相较于电工钢片更加细窄、损耗更低，因此本文选择对精度较高的Preisach模型进行改进。

为了解决Preisach模型数值求解较为耗时、复杂等问题，有学者对经典Preisach磁滞模型进行了改进。例如，Vecchia R D提出了Everett函数的概念，可有效避免经典Preisach磁滞模型双重积分的计算[14]。在此基础上，Dlala E利用极限磁滞回线实验数据构造了一阶回转曲线，提出了基于该一阶回转曲线数据辨识Everett函数的方法，从而避免了使用过多实验数据[15]，但是该模型的计算效率较低。Mayergoyz在经典Preisach磁滞模型基础上加入了可逆磁化分量，从而提高了模型的模拟精度，但其分布函数的辨识依赖于一阶回转曲线和二阶回转曲线的测量，同时求解过程中涉及求导等计算，容易产生误差[10]。另外，有学者利用Cauchy-Lorentz、Gaussian、Lognormal、Hyperbolic tangent等解析函数来近似分布函数，这种方法虽然减小了分布函数辨识的复杂度，但模拟精度相对而言较低[16 - 19]。

为了能够快速准确模拟非晶合金磁滞特性以及计算其损耗，首先，根据非晶合金极限磁滞回线实测值计算Preisach分布函数、分析分布函数基本特征，从而选择合适的解析函数对分布函数进行辨识，并对其积分得到闭合形式的Everett函数表达式，从而确定非晶合金不可逆磁化分量，这样避免了Preisach模型分布函数辨识复杂、计算耗时的问题；而后，考虑可逆磁化分量对非晶合金磁滞特性的影响，引入双曲正切函数来表征非晶合金可逆磁化分量；最终，通过线性叠加的方式建立了一种新的适用于非晶合金磁滞特性准确、快速模拟的解析Preisach模型。实验及仿真结果证明了本文所提Preisach模型的准确性以及有效性。

1 经典Preisach模型

经典Preisach磁滞模型将磁性材料的磁滞回线表示成无数个矩形磁滞算子的叠加。单个矩形磁滞算子如图1所示的矩形回线，其中β和α分别代表磁滞算子正、负向翻转的临界值，同时每个磁滞算子的磁化状态γ仅有“+1”和“-1”两个值。当外加磁场强度H作为输入且小于α时，γ=-1；当外加磁场强度H大于β时，γ=+1。将每一个磁滞算子的磁滞特性叠加后，便得到了磁性材料的磁滞特性：

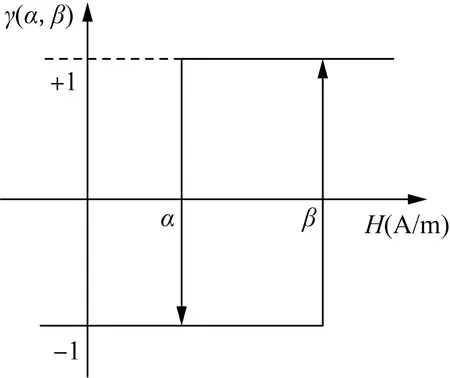
图1 单元磁滞算子

B(t)=∬Tμ(α,β)γ(α,β,H(t))dαdβ

(1)

式中：μ(α，β)为Preisach模型的分布函数，表示Preisach平面内磁滞算子的分布密度；T为三角形积分区域。磁场强度H作为输入，磁通密度B为输出。图2中分布函数μ(α，β)的积分域被阶梯线L分为两个区域S+和S-，S+内磁滞算子磁化状态γ取值为+1，S-内磁滞算子磁化状态γ取值为-1。阶梯线L上的转折点对应外加磁场强度H(t)的历史极值，当H(t)增大时，阶梯线水平上移，S+区域增大；当H(t)减小时，阶梯线垂直左移，S-区域增大。因此，式(1)可写成以下形式。

B(t)=∬S+μ(α,β)dαdβ-∬S-μ(α,β)dαdβ

(2)

为了避免经典Preisach模型中的双重积分计算引入Everett函数，其定义是在Preisach平面内对分布函数μ(α，β)进行积分，表达式如下。

E(x,y)=∬Tμ(α,β)dαdβ

(3)

式中：T为以α=β为斜边的等腰直角三角形对应的积分区域，(x，y)表示的是该等腰三角形顶点坐标，如图2中阴影区域。

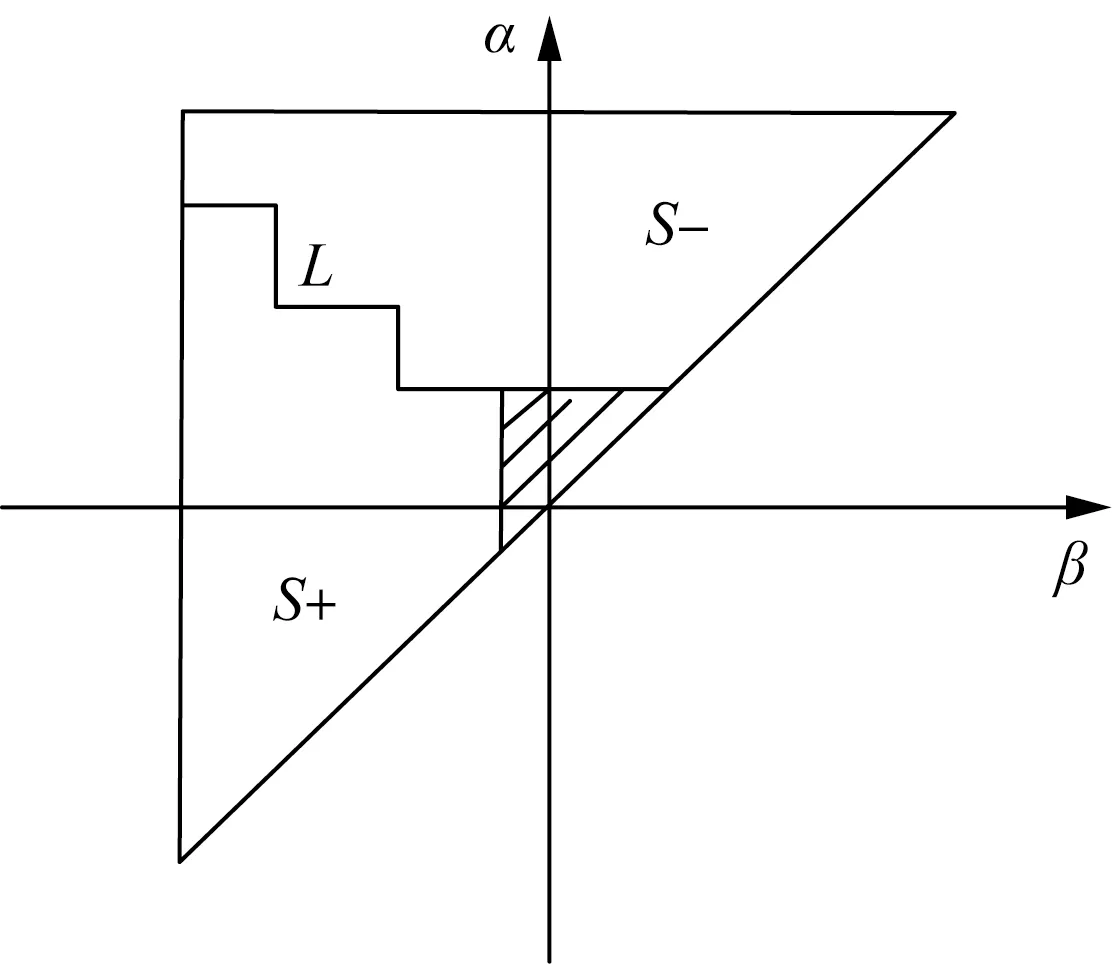
图2 Preisach模型分布函数积分域

2 解析Preisach模型

本文在经典Preisach模型的基础上，加入可逆磁化分量，如式(4)所示。其中，等号右边的第一项表示不可逆磁化分量，第二项表示可逆磁化分量，k(α)为可逆磁化分量的分布函数。

(4)

由式(2)可知，磁通密度B(t)求解的关键在于分布函数的确定。现阶段，针对分布函数的辨识大多利用一阶回转曲线或者同心磁滞回线。其中，一阶回转曲线可以通过数值方法或者实验数据生成，前者计算过程复杂且计算速度慢，后者需要大量的实验数据且测量精度无法保证；同心磁滞回线实验数据虽然测量精度比较准确，但是涉及数值积分时会放大误差。因此，本文提出利用解析函数对式(4)中的分布函数进行辨识，并基于式(3)推导出解析形式的闭合Everett函数表达式，从而计算出非晶合金磁感应强度B(t)。

首先，假设图1中的磁滞算子上升支与下降支不相关，则不可逆磁化分量分布函数μ(α，β)可近似为两个单值函数的乘积，表达式如下：

μ(α,β)=μ(α)×μ(-β)=f(α)×f(-β)

(5)

利用所选非晶合金样品实验测量的极限磁滞回线数据，基于二阶偏微分法得到离散分布函数的数值和形状，如图3所示。根据所得不可逆磁化分量分布函数的数值和形状，辨识得到式(5)中单值函数f(z)，如式(6)所示，对应的拟合结果如图4所示。

图3 Preisach模型分布函数离散值

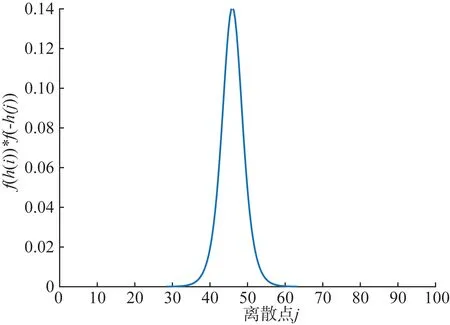
图4 Preisach分布函数拟合结果

(6)

通过调整参数a、b、c的值提高函数f(z)与非晶合金分布函数μ(α，β)的拟合精度。为使函数f(z)形式更简洁紧凑，令B=1/c，C=eb/c，A=a×C，得到第二个表达式。解析形式的分布函数表达式如下。

μ(α,β)=f(α)×f(-β)

(7)

对上述解析形式的分布函数进行双重积分，计算得到Everett函数表达式如式(8)所示。

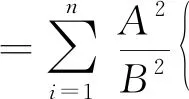
(8)

其中，L表达式为：

(9)

这种解析形式的Everett函数表达式仅包含基本的代数运算，具有运算简单、计算速度快、便于数值仿真等优点。

当外加磁场强度H(t)从负的最值-HM开始增大到正的最值HM，形成磁滞回线的上升支，此时不可逆磁化分量磁通密度Bu可通过Everett函数表示为：

Bu=-BM+2E(H,-HM)

(10)

式中BM为饱和磁通密度。

同理，当外加磁场强度H(t)从正的最值HM开始减小到负的最值-HM，形成磁滞回线的下降支，此时磁通密度Bd可表示为：

Bd=BM-2E(HM,H)

(11)

由于非晶合金的磁滞回线更加细窄，因此，通过添加更多参数变量提高非晶合金不可逆磁化分量的模拟精度，即以多项和形式表示Everett函数，n为参数变量个数，如式(12)—(13)所示。

E(x,y)=

(12)

(13)

通过上述的Everett函数表达式和式(10)—(11)，即可求得磁滞回线上任一点的不可逆磁化分量磁通密度值。首先计算磁通密度最值BM，结果如下。

BM=E(HM,-HM)=

(14)

(15)

磁滞回线上升支某一点的不可逆磁化分量磁通密度表达式为：

Bu=-BM+

(16)

(17)

磁滞回线下降支某一点的不可逆磁化分量磁通密度表达式为：

Bd=BM-

(18)

(19)

对于式(4)中的可逆磁化分量分布函数k(α)，研究表明，可逆磁化分量计算方法主要有对测量得到的B-H曲线回转点处的斜率(可逆磁导率)进行积分，以及利用含参函数来近似模拟可逆磁化曲线两种。

本文根据Mayergoyz提出的移动Preisach模型拟合的可逆磁化分量特性以及文献[20]中可逆磁化分量计算方法，利用双曲正切函数来近似计算可逆磁化分量，表达式如式(20)所示。这样不仅考虑了磁场强度输入值H(t)对可逆磁化分量的影响，而且仅需要对参数进行提取，计算过程进一步简化。

(20)

式中k1、k2、k3分别为与可逆磁化分量相关的待提取变量。

综上所述，将式(16)—(17)或式(18)—(19)与式(20)代入式(4)中对应项，便可得到适应于非晶合金磁滞特性模拟的解析Preisach模型。

3 实验验证与仿真分析

3.1 实验平台

为了验证所提磁滞模型的精度，本文选用BROCKHAUS软磁材料磁特性测量系统测量非晶合金磁环样品在不同磁感应强度下的磁滞回线。该测量系统专用于软磁材料的磁性能测量，可根据测量需求选择不同的测量线圈单元。由于该测量系统采用全数字化的数据采集系统，可实现磁场强度H与磁感应强度B的并行存储，因此保证了H和B同步测量，避免因相位差而产生的测量误差。同时，该测量系统还采用自适应负反馈算法，自动调节激励电源的输出电压，从而保证了磁滞回线等磁特性数据测量的准确性。因此，该测量系统的测量方法及结果符合国际电工委员会标准“IEC 60404- 2”。利用实测的原边电流和副边空载电压，计算磁场强度H(t)和磁感应强度B(t)，如式(21)—(22)所示。

(21)

(22)

式中：N为线圈匝数；i为初级线圈励磁电流；u为次级线圈电压；lm为等效磁路长度；S为非晶合金磁环等效截面积。

本文采用牌号为1K101的铁基非晶合金磁环[21]，参数为：内径90 mm，外径100 mm，高20 mm，质量180.45 g。测量该非晶合金磁环直流条件下不同磁密时的磁滞回线，结果如图5所示。实验测量结果发现，该非晶合金磁环饱和磁密约为1.0 T，此时对应的磁场强度在17 A/m左右。

图5 1K101非晶合金实验测量磁滞回线

3.2 解析模型参数辨识

由于解析Preisach模型涉及较多参数变量，因此关键是找到合适的参数提取算法。本文基于对现有参数提取算法[9,22 - 23]的研究，采用单目标多变量二进制遗传算法对Preisach模型参数进行辨识。对于多变量优化问题，遗传算法将各个变量的二进制码串联在一起形成码链，迭代优化后，再进行解码，提高参数提取的准确性。遗传算法目标函数如式(23)，Bcal、Bmea分别为仿真值与实验测量值。遗传算法提取解析Preisach模型参数的过程如图6所示。

图6 解析Preisach模型参数辨识流程图

通过将实验数据与仿真结果比较，选取n=3，既可以保证解析Preisach模型的准确性又可以防止参数过多造成计算量过大，由此得到的参数辨识结果如表1所示。

表1 n=3时，非晶合金解析模型辨识参数

(23)

3.3 磁滞特性模拟与仿真

为了验证本文所提解析Preisach模型的准确性，将表1中参数值分别代入非晶合金不可逆磁化分量和可逆磁化分量表达式中，利用MATLAB对1K101铁基非晶合金磁环静态磁滞特性进行仿真，将拟合结果与实验测量数据以及经典Preisach模型仿真结果进行对比，结果如图7所示(Bp表示磁滞回线峰值磁密)。

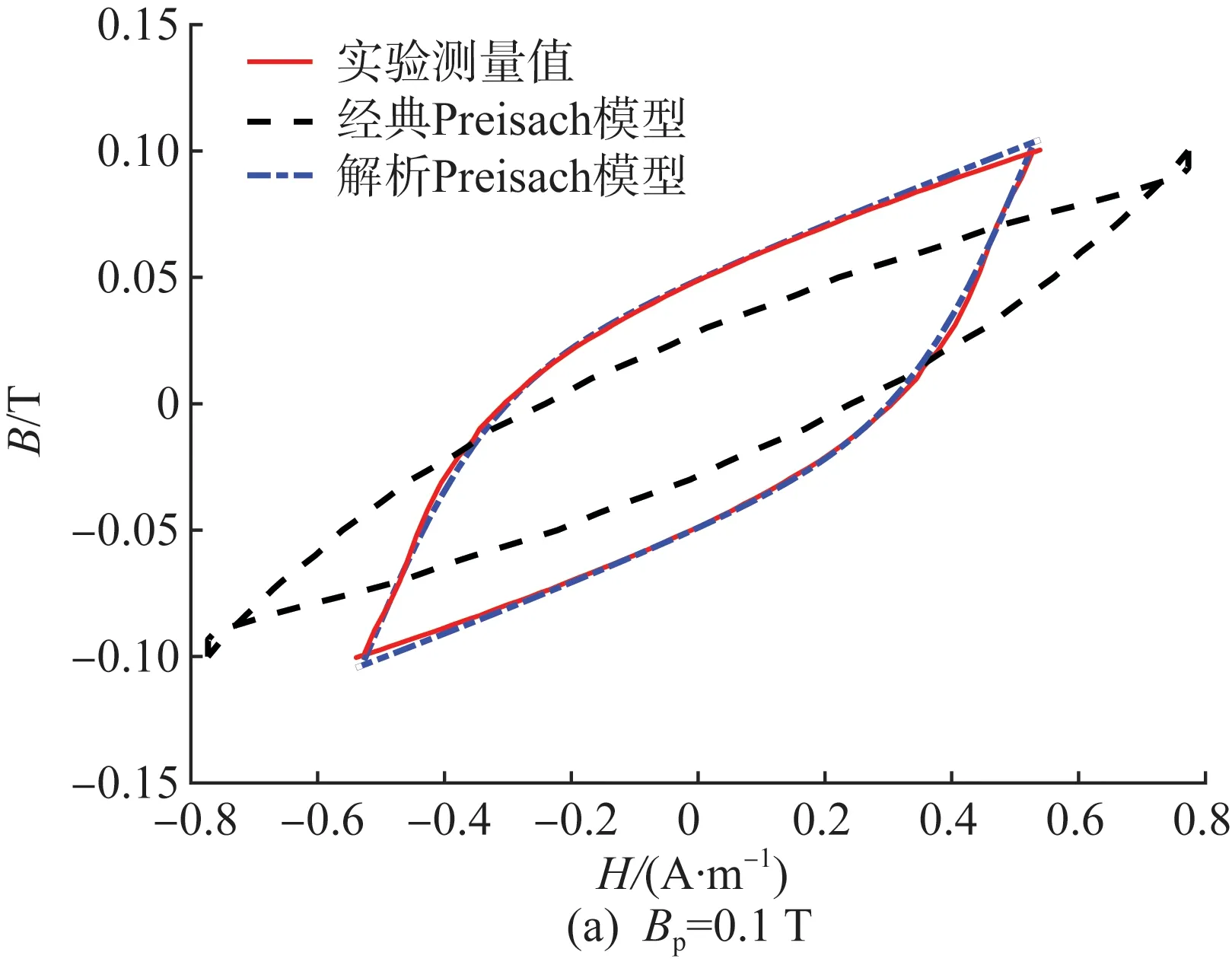
图7 不同磁密下的仿真结果

从以上结果可以看出，无论在低磁密时还是饱和磁密附近，相对于经典Preisach模型，本文所提解析Preisach模型拟合效果都更好，精度更高。同时，解析Preisach模型由于仅涉及简单的数值计算，因此计算速度相比于经典Preisach模型大大提升。

表2 损耗计算结果

从损耗对比结果可以看出，解析Preisach模型计算误差均控制在10%以内，证明了该模型的计算精度较高。考虑到该解析模型便于数值仿真、准确性高且计算速度快，因此满足实际工程要求。

4 结论

为了可以准确快速地模拟非晶合金磁滞特性以及计算其损耗，本文提出了一种解析Preisach模型，得到以下结论。

1)本文首先根据非晶合金极限磁滞回线实测值计算Preisach分布函数离散值以及分析分布函数基本特征，利用特定的解析函数对分布函数进行辨识，并对其积分得到闭合形式的Everett函数表达式，从而确定非晶合金不可逆磁化分量；而后，根据Mayergoyz提出的移动Preisach模型拟合的可逆磁化分量特性，考虑到可逆磁化分量对非晶合金磁滞特性的影响，利用双曲正切函数计算非晶合金可逆磁化分量；最后，通过线性叠加的方式建立了解析Preisach模型。

2)基于构建的解析Preisach模型对1K101铁基非晶合金磁环在不同磁密下的磁滞回线进行模拟，发现仿真结果与实验测量磁滞回线差距较小，且损耗计算误差均控制在10%内。验证了该磁滞模型不仅可准确地模拟非晶合金磁滞特性、计算损耗，而且在分布函数辨识、数值实现、计算精度等方面都有较大提升，满足实际工程中对非晶合金磁滞特性模拟的要求。