间接地下滴灌土壤水分运移规律研究

曹 睿，贾生海，赵 霞，白有帅，许春娟，王艳萍

(1.甘肃农业大学水利水电工程学院，甘肃 兰州 730070；2.民勤县给排水管理站，甘肃 民勤 733300)

滴灌节水增产效果是当今世界上学者普遍认同的，也是当前农业及林果业节水灌溉使用较多的一种灌溉方式[1- 4]。随着生产规模的扩大，滴灌时的地表棵间蒸发直接影响作物根系对水分的吸收利用。间接地下滴灌技术是在滴灌基础上发展起来的新型节水灌溉技术，由地表滴灌系统和布设在滴头下方的导水介质2部分组成，其优点在于能把作物需要的水分快速导入根部附近。1997年Meshkat等提出的砂管灌是间接地下滴灌技术的起源，Meshkat等通过室内实验发现砂管灌可以明显降低土壤地表蒸发[5]。2004年Yanni等以果树为研究对象进行灌溉试验研究，研究方法与Meshkat使用的相似，得出灌溉结束的14d内，同一灌水量下垂直砂覆盖灌比常规滴灌的灌水效果显著[6]。国内学者开展间接地下滴灌技术较晚，安巧霞等研究间接地下滴灌在不同流量下的变化规律，发现湿润体形状近似椭圆体，同一灌水时间下，滴头流量越大，湿润体体积越大；同一灌水量下，滴头流量越大，湿润体体积越小[7]。李道西等通过室内实验，研究了灌水要素(灌水量和滴头流量)对土壤水分运动的影响情况，发现同一灌水量下，滴头流量增大，保水性差的砂土垂直方向湿润锋的运移明显，而保水性较好的轻壤土水平方向上的运移更加明显[8]。吴继强等研究了大孔隙对土壤水分入渗特性的影响，发现大孔隙的连通性对土壤水分的优先入渗起主要作用[9]。目前针对不同粒径导水材料对土壤湿润体情况的研究较少。鉴于此，本文通过对不同砂管粒径下的土壤水分运移规律研究分析，结合灌水结束24h后的土壤含水率情况，以期获得更好的数据为田间实验提供依据。

1 材料与方法

1.1 试验场地与装置

室内试验场地为甘肃农业大学工科楼土工实验室，试验在自制的有机玻璃箱中进行(图1)，规格尺寸为120cm×55cm×75cm(长×宽×高)的长方体无盖土箱。滴灌水源装置为马氏瓶，保证试验所需的稳定恒压水源，通过引水管连接恒通量水管进行室内实验[10]。

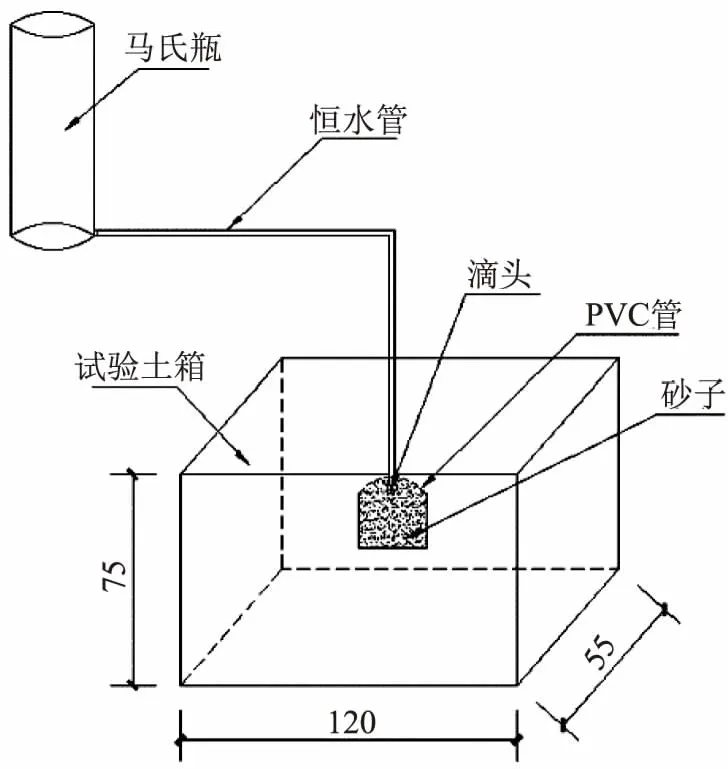
图1 试验装置图(单位：cm)

1.2 试验设计

试验所用土样取自民勤县勤锋林业试验站枣树基地，取回后风干，过2mm筛，分析实验所用土壤粒径得出试验土样为容重1.5g/cm3的沙壤土。将土样按每层5cm厚夯入土箱中，导水装置为砂管，制作时采用直径为10cm的PVC管的一半作为边界，扣到土箱边，土样装满土箱后将砂子装入PVC管，装填石英砂完毕后抽出PVC管形成砂管，砂管深度为20cm。试验过程中使用秒表计时，按拟定时间间隔(3、10、30、60、120、180min)，用黑色记号笔在土箱上描绘出湿润锋位置，并且用钢尺测量各个时刻水平湿润锋和垂直湿润锋的运移距离[11]。滴灌过程中以时间控制灌水量，当灌水时长达到3h时停止灌水。试验砂采用3个粒径，分别为1～2mm、2～3mm、3～5mm。处理情况见表1。土壤含水率使用烘箱烘干法测定，灌水结束24h后取土，取土时采用直径1cm的土钻，在导水装置外围沿水平方向每隔5cm设置一取样点，每个点处垂直向下每隔5cm取样，共计取样80个。

表1 试验方案

1.3 数据分析

采用Origin2018、Excel 2010、SURFER15.0软件进行统计分析。

2 结果与分析

2.1 土壤中湿润锋的运移

2.1.1湿润锋的运移形状

为了清晰准确的观察湿润体的形状，将实测的湿润锋运移曲线表现在二维坐标系中[12- 13]。本试验中3个处理的灌水时间和灌水量相同，因此对湿润锋形状的影响基本相似，故选择其中1个处理绘图并进行分析，如图2所示即为T2处理所对应的湿润锋运移曲线。观察图2可以发现，T2处理下湿润锋的形状近似表现为椭球体，这是由于均质土壤各向同性的特点，所以呈现出左右基本对称的现象。水平方向及垂直方向上的湿润锋随着灌水时间的增加而逐渐增大。灌水初期，水平方向湿润锋的运移距离大于垂直方向。随着灌水时间的增加，在y方向上，湿润锋垂直向下的运移距离要大于垂直向上的运移距离[14]。灌水结束后，4个方向中运移距离最大的是水平方向，运移距离最小的是垂直向上方向，这是垂直向上方向上水自身的重力与土壤吸力共同作用的结果。灌水结束的24h中湿润锋运移较灌水时明显减缓，运移距离较小，24h后垂直向下方向的总运移距离大于水平方向[15]。

图2 土壤湿润锋的运移

2.1.2湿润锋运移距离随时间变化情况

如图3—4所示是湿润锋运移距离随时间变化的情况。开始灌水时，土壤中含水率较低，土壤入渗能力大，入渗速度快。随着灌水的增加，土壤中水分不断积累，土壤中含水率提高，入渗能力较灌水初期减弱，入渗速度减缓。入渗初期，水平方向的入渗速度快，入渗距离比垂直向下的入渗距离大，这是由于灌水初期，土壤水受到的土壤的持水作用大于重力产生的作用，即土壤基质的吸附力和毛管力产生的势能大于重力产生的势能。随着入渗的进行，湿润锋在水平方向的运移距离依然大于垂直向下方向上的运移距离[16]，这是土壤容重与流速共同影响的结果，本文所用土壤属于质地比较粗的沙壤土，容重越大，土壤非饱和导水能力越大，湿润锋在水平方向上的运移就会越快；此外流速也是影响因素之一，当流速大于土壤入渗能力时，竖直向下方向的入渗变慢，地表积水会引起水平运移距离的增大。

由图3可以看出，土壤容重、初始含水率、灌水量相同，导水装置所用材料中粒径为2～3mm的砂子产生的水平运移距离大于砂子粒径为1～2mm和3～5mm的运移距离。图4中各个处理下的运移距离差异不明显，灌水结束后入渗距离最大的是T2处理，即导水装置砂子粒径为2～3mm。这是由于粒径小的砂子渗透系数小，入渗慢，运移距离小，而粒径较大的砂子，初始入渗较快，但会在砂管底层与土壤的交界处出现积水，向下的入渗距离较T2处理小。对水平入渗距离(x)、竖向入渗距离(y)与灌水时间(t)进行拟合，见表2。由表2可以看出湿润锋水平、竖向入渗距离与灌水时间均存在着显著的二次函数关系，决定系数(R2)均大于0.97。因此当土壤基本性质已知，流量固定的情况下，可以通过灌水时间来确定湿润锋各个方向运移的距离，从而达到精准灌溉的目的。

图3 湿润锋水平入渗距离变化过程

图4 湿润锋竖向入渗距离变化过程

2.2 灌溉停止后湿润体的变化规律

灌水结束后，地表积水慢慢消失，土壤入渗过程接近结束，但由于湿润体内部及湿润体与周围土壤之间存在着水势梯度，土壤水分的运移并没有结束，即土壤水分进入再分布阶段，湿润体会继续扩散，在水平方向和竖直方向上均有所增加，土壤水的再分布过程是非饱和状态下的土壤水分运动，最后会趋于平稳[17]。滴灌结束后24h湿润体尺寸的变化见表3。

表3 滴灌停止后湿润体尺寸的变化

分析表3中数据可得：灌水结束的24h内，湿润体运移距离变化较明显。水平方向上的平均相对变化值为21.9%，垂直方向上的平均相对变化值为29.8%，比水平方向上的扩散变化大7.9%。产生这一现象的原因是土壤水分的再分布过程中，在垂直方向受土壤基质(固体)的毛管力和吸附力与重力共同作用，而在水平方向上仅受土壤基质的吸附力和毛管力作用[18]，所以再分布过程垂直方向上的运移速率比水平方向的大，这也是湿润体呈半椭球状的原因之一。

2.3 土壤含水率的分布规律

如图5所示为不同处理灌水24h后土壤含水率的变化情况。由于导水材料粒径不同，3种处理的含水率分布有明显的差异。间接地下滴灌下水分从导水材料底部及边界向周围入渗，随着入渗的进行砂管底部及边界的水分接近饱和，水分就会向更深处入渗。灌水结束24h后，在水平方向上，距离滴头越近，含水率越高，距离滴头越远，含水率越低；在垂直方向上，含水率自上而下先增大后减小。

表2 湿润锋运移距离的拟合方程参数

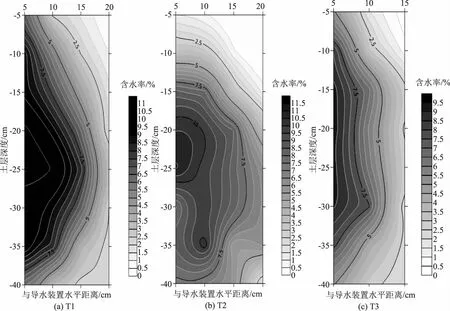
图5 灌水结束24h后土壤含水率变化的影响

从图5可以看出，在导水材料粒径为1～2mm的条件下，土壤最大含水率出现在图5(a)中坐标(5，-25)处，即砂管底部以下5m处，最大含水率为10.89%；在导水材料粒径为2～3mm的条件下，土壤最大含水率出现在图5(b)中坐标(5，-25)处，和T1处理一致，最大含水率为11.07%；在导水材料粒径为3～5mm的条件下，土壤最大含水率出现在图5(c)中坐标(5，-20)处，即砂管的底部，最大含水率为9.31%[19]。

结果表明，3种不同粒径导水材料中，土壤整体含水率最大的为T2处理，即砂子粒径为2～3mm的处理。

3 结论

(1)不同粒径下湿润锋运移形状基本呈椭球体状，水平及垂直方向上湿润锋随着灌水时间的增加而增大。灌水结束24h后，水平方向上滴头处含水率最大，距离滴头越远含水率越小；垂直方向上含水率先增大后减小，最大含水率均出现在地表以下20～25cm中。

(2)砂子粒径为1～2mm时，出现地表积水，在干旱地区推广会增大蒸发；砂子粒径为3～5mm时，砂砾空隙太大，入渗不均匀，通气管内气性太大，增大蒸发；砂子粒径为2～3mm时，入渗达到了作物主要根系层，蒸发小，含水率高，因此选择2～3mm的砂子，以更好地指导河西地区的实际生产。