基于影响矩阵的斜拉桥成桥索力优化方法分析

阴文蔚

（中铁第五勘察设计院集团有限公司，北京 102600）

1 引言

斜拉桥具有造型优美、结构简洁、跨越能力强、造价经济等特点，近年来在桥梁工程中得到越来越广泛的应用和发展。斜拉桥是由主梁、主塔和斜拉索组成的组合体系结构，拉索的存在使得斜拉桥成为“牵一索而动全桥”的高次超静定结构。由于索力是可以调整的，不同的索力对应斜拉桥结构不同的受力状态，故可以通过优化求解找到一组索力，使得斜拉桥的各项受力指标得到设计者期望的合理值，上述求解过程即为斜拉桥的索力优化。

2 斜拉桥索力优化方法

斜拉桥常用的索力优化方法主要有3 种，即指定受力状态的索力优化、索力的无约束优化和索力的有约束优化。

斜拉桥索力优化的指定受力状态法主要包括刚性支承连续梁法和零位移法。刚性支承连续梁法就是将索梁交接点视为刚性连接，按常规梁求出这些刚性支承的反力，再根据斜拉索的竖向分力与刚性支点反力相等确定索内力，该内力即为优化后的索力。零位移法以索梁交点处位移为零为优化目标，求解结构在荷载作用下成桥状态对应的索力，该过程即为基于零位移法的斜拉桥成桥索力优化。

斜拉桥索力的无约束优化法主要包括弯曲能量最小法和弯矩最小法。弯曲能量最小法是以结构的弯曲应变能最小作为优化目标，对梁、塔等的轴向、弯曲刚度作相应调整后求解荷载作用下结构的效应，得到一组优化索力，将优化问题转变为结构的一次分析问题。弯矩最小法是以结构弯矩平方和最小为优化目标，求解荷载作用下斜拉索的索力，其缺点是无法考虑构件截面特性对优化结果的影响。

斜拉桥索力的有约束优化法主要包括用索量最小法和最大偏差最小法[1]。用索量最小法是以斜拉索的用量最小作为优化目标，用设计者所关心的控制截面的内力、位移等效应的合理取值作为约束条件进行优化求解。最大偏差最小法以可行域中参量与期望值的最大偏差达到最小作为优化目标，作为一个隐式约束优化问题最后可归结为一个线性规划问题[2]。

综上，指定受力状态法力学概念明确，程序实现较为简单并均可归结为求解一组线性方程组，但该方法基于梁的受力状态建立数学模型，未考虑塔的影响，也无法对塔的受力状态做出评判。无约束的弯曲能量最小法和弯矩最小法的优点在于对判断成桥状态是否合理给出了一个既明确又便于数学表达的目标函数，但其缺点是缺乏必要的限制、约束条件而导致最终不能得到理想的结果。有约束优化的用索量最小法其难点在于选择合理的约束条件，约束条件选择的优劣直接决定了优化结果的合理性。

对于一个承载结构来说，合理的受力状态下其内力、应力、位移等效应值应当在由结构体系和材料性能确定的合理的取值范围内，故合理的受力状态并非由单一的指标确定的，所以用某个单一的性能指标进行优化是很难获得合理的成桥索力的。基于此，文献[2]的作者提出了基于影响矩阵的索力优化法。

3 基于影响矩阵的索力优化法

影响矩阵法是以斜拉桥索、梁、塔的控制截面的内力、位移等多种效应值作为优化目标，利用影响矩阵进行多目标优化，求解得到成桥状态下满足上述优化目标的一组索力，该方法克服了上述优化法目标单一的缺点，实现多目标下优化结果的统一。

3.1 基本定义

受调向量：斜拉桥索、梁、塔控制截面上m 个相互独立的元素所组成的列向量[3]。该列向量的元素可以是截面内力、应力或位移。这些元素在优化过程中接受调整，最终达到设计师期望的目标状态。受调向量记为：

式中，bi为第i 个独立的受调元素。

施调向量：为使受调向量相应发生变化而定义的可实施调整的l 个独立元素所组成的列向量(l≤m)，记为：

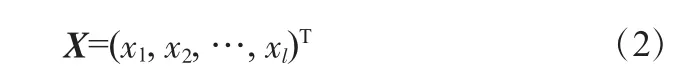
式中，xi为第i 个独立的施调元素。

施调元素一般为杆件内力。

影响向量：施调向量中第j 个元素xj发生单位变化时引起受调向量B 相应的变化向量，记为：

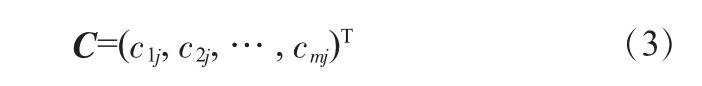
式中，c1j,c2j,…,cmj分别为第j 个施调元素xj发生单位变化时相应m 个受调元素对应发生的变化量。

影响矩阵：l 个施调向量分别发生单位变化，引起的l 个影响向量依次排列形成的矩阵，记为：

在影响矩阵[C]中，其元素可取为内力、应力或位移，影响矩阵是这些力学元素混合组成的矩阵，根据线性叠加原理，影响矩阵[C]、受调向量B 与施调向量X 之间建立如下关系：

3.2 基本思想

基于影响矩阵的斜拉桥索力优化法取拉索的索力作为施调向量，取墩、梁、塔的截面内力、应力或位移作为受调向量。索力优化结果其实质就是当受调向量达到目标值时基于影响矩阵所确定的施调向量的取值，故受调向量目标值的确定是求解合理成桥索力的关键[4]。前文已述，一个受力状态的合理应当是在荷载作用下结构的内力、应力、位移等效应值的合理。对于一个优化问题来说就是受调向量目标值的合理，因此，优化问题的关键就是如何在数目繁多的效应指标中找到一组数值作为优化目标。为避免优化目标选择的盲目性，提高优化效率，该目标约束应具备如下几个条件：

1）优化目标是该结构受力工况下荷载效应的真实存在，这是优化成功的前提条件；

2）约束指标的选取及其取值应有利于求解，即求解过程迭代次数少；

3）施调向量的个数应不大于受调向量的个数，这是确保数学模型有解的必要条件。

前文已述，无约束的弯曲能量最小法其优点在于可以推导出一个既便于数学表达又符合设计师要求习惯的目标函数，故可以通过该方法快速获得惯性截面的一组最小弯矩值，再以此弯矩为优化目标利用基于影响矩阵的多约束优化法进行索力优化。索力优化完成后查看各效应值的变化情况，根据首次优化结果并结合优化的侧重点调整目标后再次优化，直至得到理想的结果。

4 实例分析

4.1 工程背景

某独塔中央索面预应力混凝土斜拉桥，采用墩塔梁固结体系，跨径组合为2×98 m，桥面宽度为35.3 m。主梁采用单箱5 室箱梁，斜拉索锚固区主梁高3.4 m，主塔总高为71.4 m，结构总体布置如图1 所示。

图1 桥型总体布置图(单位：cm)

全桥共13 对、26 根拉索，结合本桥斜拉索沿顺桥向对称的特点，将模型中关于主塔中心线对称的索合并为一组，故归并后模型共13 组索，从边墩向主塔方向编号依次为S1～S13。

4.2 优化过程分析

如前文所述，首次优化可采用成桥状态下斜拉索锚固点主梁的弯矩值作为优化目标，该弯矩值可采用无约束的弯曲最小能量法计算得到。利用该方法求解弯矩时梁和塔的弯曲刚度不变，抗拉、压刚度调整为无穷大[5]（一般通过放大塔、梁、索截面面积104～106倍实现），计算所得弯矩即为首次优化目标弯矩。按照上述方法修改、放大截面面积，经计算，本桥拉索锚固点主梁弯矩值如表1 所示。

从表1 弯矩计算结果可以看出，受无索区的影响，两侧边索锚固点主梁弯矩较大，除此之外，成桥状态下拉索锚固点主梁的弯矩值在-2 500～-3 500 kN 范围内，以此范围弯矩值为优化目标进行首次优化。经计算，优化结果如图2～图3 所示。

表1 拉索锚固处主梁弯矩汇总表

图2 第1 次优化斜拉索索力图

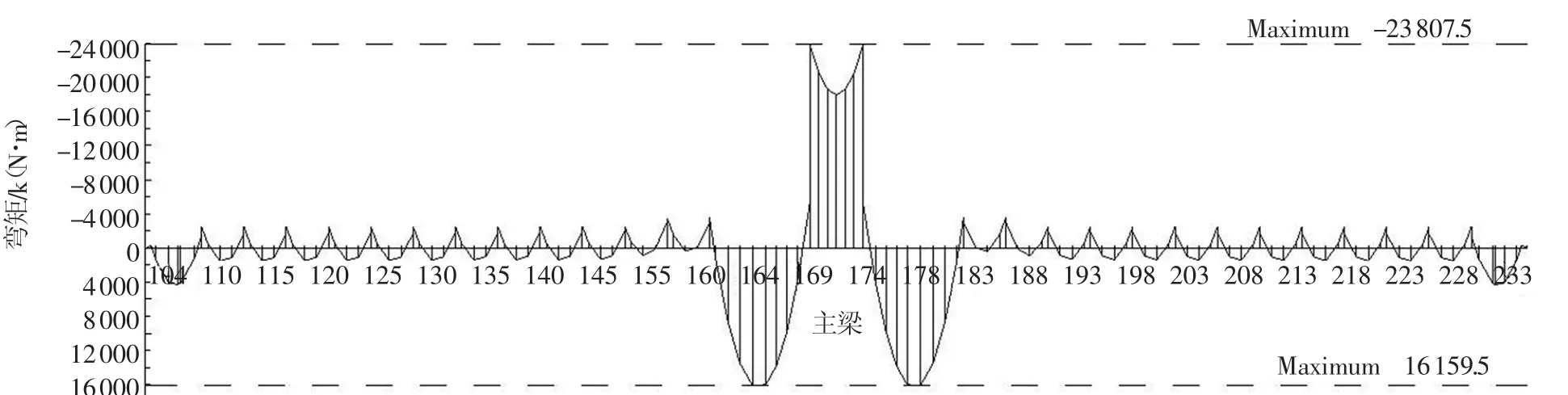
图3 第1 次优化后主梁弯矩图

从图2 中可以看出索力分布符合长索索力大、短索索力小的分布原则，S1 和S13 号索受无索区及墩、塔约束的影响出现较大突变，故该位置采用弯矩作为优化的目标显然是不合理的，修改索力突变拉索的优化目标为其索力期望值进行二次优化，优化结果如图4～图6 所示。

图4 第2 次优化后斜拉索索力图

图5 第2 次优化后主梁弯矩图

图6 第2 次优化后主梁竖向位移图

从图4～图6 中可以看出，经过二次优化后索力分布较为均衡，主梁受力均匀且承受较小的弯矩，主梁最大位移为5 mm，各项受力指标均较为合理，是一个理想的优化方案。

5 结语

本文优化方法概念明确、计算简便，可快速确定斜拉桥成桥索力，有效避免了索力优化的盲目性。经实例验证采用本文方法优化后斜拉桥索力分布、结构受力及变形等结果均较为理想，具有较高的工程应用价值。

需要说明的是，上述优化的成桥状态只是一个初步、大致合理的成桥状态，在此基础上还要考虑活载引起的弯矩可行域及预应力的影响后继续优化，方能确定最终的合理成桥状态。由于该步骤需要结合工程实际情况及优化的侧重点来确定，在此本文不做进一步的阐述。