基于FTA-BN的地铁车站施工风险评价研究

郑逸雪

(中国矿业大学(北京)，北京 100083)

0 引言

随着城市化进程的加快，城镇人口急剧增长，地面交通的客运量已经无法满足人们的出行需求。为了缓解地面交通压力，地铁得到快速发展。如何最大限度地保证地铁车站施工安全，避免人员伤亡、经济损失和工期延误，是该领域重要的关注点。

学者们对地铁车站施工风险评价展开了诸多研究。夏润禾等[1]采用前因-行为-结果分析法对地铁车站施工人员不安全行为的形成及影响因素进行分析，构建地铁车站不安全行为风险管理模型。郭健等[2]运用模糊综合评价法进行风险评估，得出地铁车站深基坑施工风险等级。郭循杰等[3]采用综合评价法、模糊层次分析法和定性分析法分别对合肥地铁车站施工进行风险评估。蒋频等[4]通过矩阵线性变换的原理构建主成分分析数学模型，计算风险类别综合得分，并通过得分高低反映风险大小。潘海泽等[5]将突变级数法应用在地铁车站基坑施工风险分析中，得出基坑施工风险发生概率。

地铁车站施工风险评价的相关研究以定性分析为主，定量分析不够深入，且无法准确分析不确定性因素。贝叶斯网络模型是一种不确定性的因果推理模型，在处理不确定性问题上有一定的优势，在医疗诊断领域[6-7]、生命科学领域[8-9]、工业和工程控制领域[10-11]得到了广泛的应用。本文考虑到贝叶斯网络能进行双向推理和较好地解决不确定性问题，提出一种基于事故树分析法(FTA)和贝叶斯网络(BN)的地铁车站施工风险评价模型。结合实例，通过事故树向贝叶斯网络转化降低BN模型构建的难度，运用BN模型进行地铁车站施工风险推理，预测地铁车站施工风险发生的概率，并诊断出造成地铁车站施工风险发生概率最大的致险因素。

1 FTA-BN模型构建

1.1 事故树分析法

事故树分析法是一种演绎推理法，通过事故树进行深入分析，综合判断导致事故发生的直接原因和间接原因[12]。一个完整的事故树包括顶事件、中间事件和基本事件，事件之间的逻辑关系由“与”门、“或”门连接。基本事件和顶事件只有两种状态，即事件发生或不发生。

1.2 贝叶斯网络理论

贝叶斯网络是基于概率论和图论的推理模型，是由多个节点组成的有向无环图，节点间的逻辑关系用有向箭头表示，适用于对不确定性概率事件进行推理分析。

1.3 事故树向贝叶斯网络映射

运用事故树分析法能够深刻地把握系统内各个事件之间的逻辑关系，并通过计算得出顶事件的发生概率，但不能进行多态分析，所有事件只有发生与不发生两种状态，而事实上许多事件都存在着多种状态。贝叶斯网络能够进行多态性分析，且推理计算比事故树简易，具有更广泛的适用性，但在模型构建上存在一定的难度，因此通过将事故树向贝叶斯网络映射，降低贝叶斯网络建模的难度。事故树向贝叶斯网络映射的基本步骤如下：

(1)事故树中的事件对应贝叶斯网络的节点，相同事件归为一个节点。

(2)事故树中事件间的逻辑门对应贝叶斯网络节点间的有向边。

(3)由事故树中的逻辑门规则确定贝叶斯网络的条件概率表。

(4)事故树中的基本事件发生概率与贝叶斯网络根节点的先验概率一一对应。

事故树向贝叶斯网络映射过程如图1所示。

2 工程应用

2.1 工程概况

某地铁车站工程为地下两层分离岛式车站，采用“洞桩法”逆筑施工，每侧为单跨拱形断面，车站右线主体长度397.5m，左线主体长度350.64m。

2.2 地铁车站施工风险因素分析与事故树建模

通过大量文献研究，结合实际工程概况，得出造成地铁车站施工风险的直接原因包括施工环境风险、施工技术风险、施工人员及管理风险、施工机械设备风险、勘察设计风险，并对这些风险进行深入分析得到地铁车站施工风险事故树，如图2所示，各编号的含义见表1。

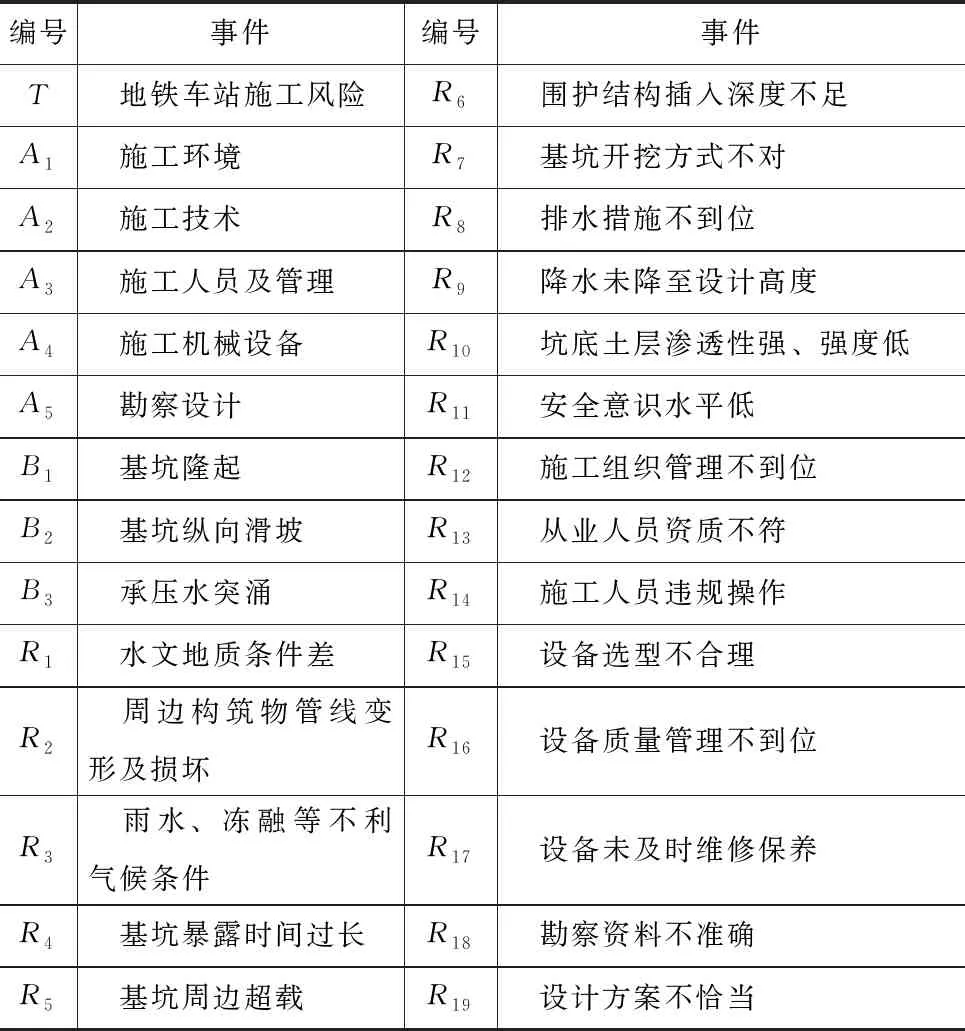
表1 地铁车站施工风险事故树各编号的含义

2.3 地铁车站施工风险FTA-BN模型构建

由构建的地铁车站施工风险事故树，可以得到地铁车站施工风险贝叶斯网络结构，如图3所示。

结合实际工程概况，通过查阅相关文献资料及专家打分的方法确定地铁车站施工风险事故树模型中基本事件发生概率。依据事故树向贝叶斯网络映射的原理，得到地铁车站施工风险贝叶斯网络模型的先验概率。地铁车站施工风险因素的先验概率见表2。

表2 地铁车站施工风险因素的先验概率

根据事故树的逻辑门规则可以得出贝叶斯网络所有非根节点的条件概率表，由于篇幅有限不一一列出。以A1节点为例，其对应的条件概率见表3。R1、R2、R3节点状态为发生时表示为Y，节点状态为不发生时表示为N。

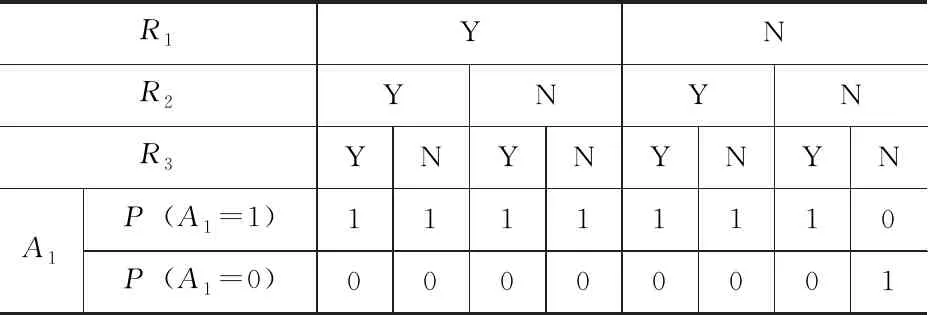
表3 贝叶斯网络A1节点条件概率表

2.4 基于正向推理的风险预测

基于上述构建的FTA-BN模型进行正向推理，可以预测地铁车站施工风险发生的概率。在贝叶斯网络中输入根节点的先验概率和非根节点的条件概率，概率就会随着贝叶斯网络从根节点传递到叶节点，从而得出叶节点的发生概率。通过正向推理可以得出地铁车站施工风险发生的概率P(T=Y)=32.2%。

为了更准确地表述地铁车站施工风险概率大小，假设概率为P，将概率划分为5个等级，分别对应5个概率区间[13]，见表4。根据表4可知，地铁车站施工风险概率等级为Ⅳ级，项目整体风险水平低。

表4 风险概率等级对应的概率区间

2.5 基于反向推理的风险诊断

在施工过程中，观察到地铁车站施工风险出现时，可以通过将贝叶斯网络中叶节点的状态设置为“发生”，即叶节点状态为P(T=Y)=1，进行反向诊断推理，得出各个风险因素的后验概率，见表5。在风险诊断过程中，后验概率可以作为风险因素重要度的判断依据，通常选取后验概率较大的风险因素作为致险因素进行重点防控。

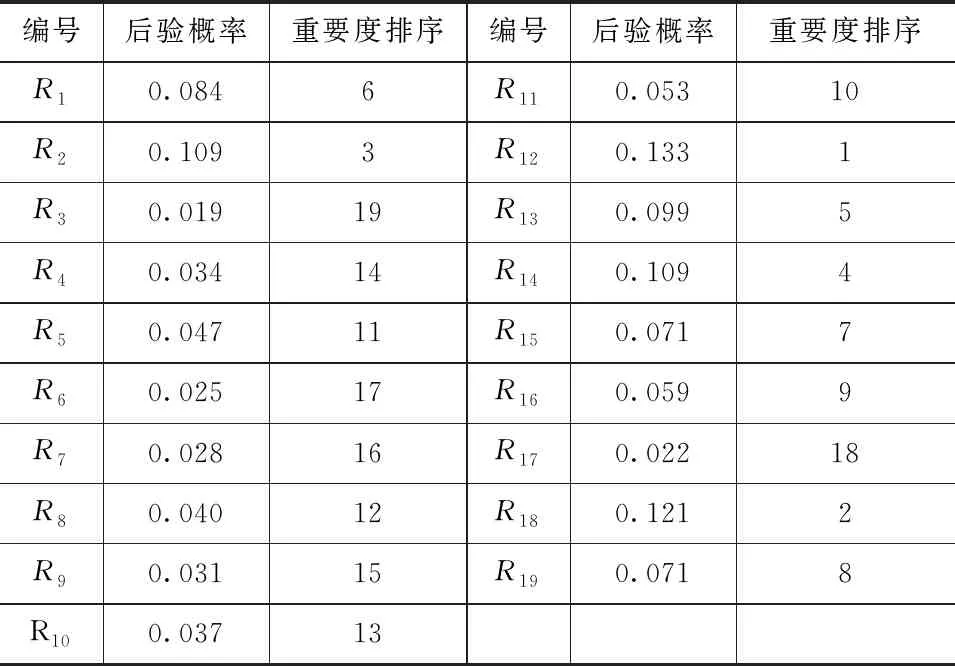
表5 风险因素的后验概率及重要度排序

若在施工过程中发现地铁车站施工风险发生，根据表5的后验概率和重要度排序可知，R12(施工组织管理不到位)的后验概率(P(R12=Y)=13.3%)最大、重要度排序最靠前，是导致地铁车站施工风险发生概率最大的因素，因此优先对该风险因素进行排查。若排查后发现R12(施工组织管理不到位)发生，则该节点状态确认为P(R12=Y)=1，应立即采取应对措施，防止情况进一步恶化。在R12这一风险因素得到有效控制后，应再次判断该项目是否处于风险状态，若地铁车站施工风险仍然发生，说明还存在其他造成地铁车站施工风险发生的因素，应重新对该项目进行诊断推理。即在风险事件发生(P(T=Y)=1)和存在施工组织管理不到位(P(R12=Y)=1)的情况下，反向推理计算其他节点的后验概率，如图4所示。从图4可以看出，此时R18(勘察资料不准确)的后验概率最大，为3.9%，则后续应重点排查R18风险因素。根据R18的排查结果，在贝叶斯网络中更新节点状态，再次进行诊断推理，按照这个流程对风险因素逐一进行排查，直到地铁车站施工风险得到控制为止。

通过诊断推理可以得出，R12(施工组织管理不到位)、R18(勘察资料不准确)、R2(周边构筑物管线变形及损坏)、R14(施工人员违规操作)为导致地铁车站施工风险发生概率最大的致险因素。因此，在施工过程中要针对这些风险因素及时采取相应的措施，避免造成更大的损失。在施工人员及管理方面，要制订完善的施工安全管理方案，落实施工组织管理的控制和监督工作；营造良好的安全生产氛围，对违规行为进行检查、评比、公布，对违规者采取处罚措施。在勘察设计方面，要加大勘察经费和人员的投入力度，保证勘察资料的准确性，提高勘察调研质量。在施工环境方面，要合理布置沉降监测点，对构筑物和管线沉降进行实时监测与分析。

3 结语

地铁车站项目施工过程受复杂地质环境、工程环境和高密度人员作业的影响，风险因素众多、不确定性大，而贝叶斯网络在解决不确定性上有很大的优势，适用于地铁车站施工风险评估。本文将FTA-BN模型引入地铁车站施工风险评估领域，运用事故树降低贝叶斯网络的建模难度，建立地铁车站施工风险FTA-BN模型，并结合实际工程案例，得出以下结论：

(1)运用贝叶斯网络进行正向推理，可以预测地铁车站施工风险发生的概率，有助于施工方直观了解项目的整体风险水平，从而预防风险事件的发生。

(2)运用贝叶斯网络进行反向推理，可以诊断出地铁车站施工风险发生的致险因素，以便及时采取应对措施，避免造成更大的损失。

(3)该地铁车站项目施工风险发生的概率为32.2%，项目整体风险水平低。施工组织管理不到位、勘察资料不准确、周边构筑物管线变形及损坏、施工人员违规操作是地铁车站施工风险发生的致险因素。因此，在施工过程中要将这些风险因素作为地铁车站施工风险管理的重点。