三种群竞争系统最小波速的线性决定性
2022-03-08王飏李红亮
王飏,李红亮
(山西大学 数学科学学院,山西 太原 030006)
0 引言
本文我们将考虑一类如下的三种群反应扩散竞争系统

其中u(x,t),v(x,t),w(x,t)分别是三个不同种群的密度,di,ri(i=1,2,3)分别代表各个种群的扩散系数和出生率,bij代表种群间的竞争强度,(i,j)=(1,2),(3,2),(2,1),(2,3)。事实上,这个系统描述了种群v分别与种群u,w竞争,而种群u和w之间不存在任何关系。
在本文中,我们假设bij满足
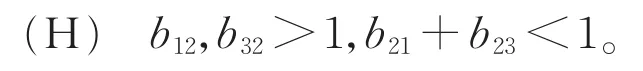
此时,系统在集合 {(u,v,w)|0≤u,v,w≤1}中只有五个边界平衡点:(0,1,0),(1,0,1),(0,0,0),(1,0,0),(0,0,1),正如Guo等人在文献[1]中所述,条件(H)表示种群u,w的竞争能力都比v弱。因此,我们考虑系统(1)连接平衡点(1,0,1)和(0,1,0)的行波解,这个行波解描述了种群v入侵种群u和w的过程。为了证明该行波解的最小波速的线性决定性,我们首先作变换u*=1-u,v*=v,w*=1-w(为了简便,省略了“∗”),那么(1)转化为如下合作系统,
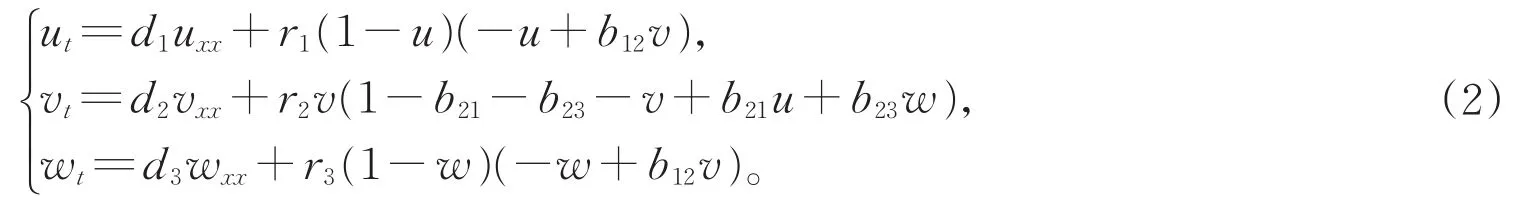
其次,我们介绍系统(2)连接(0,0,0)和(1,1,1)的行波解,即系统(1)连接(1,0,1)和(0,1,0)的行波解。事实上,如果向量值函数
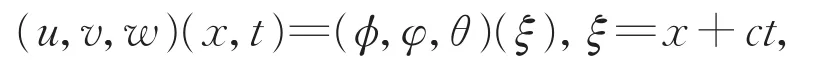
满足如下的常微分方程
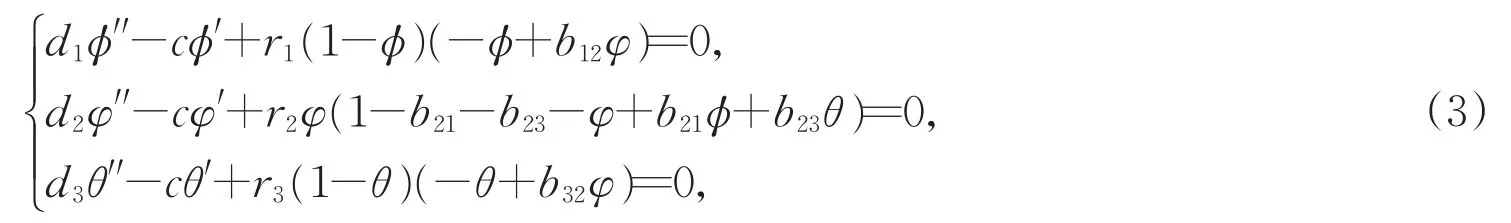
及边界条件
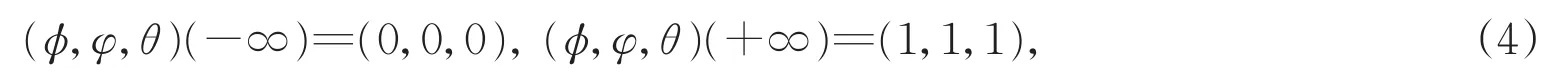
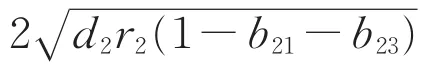
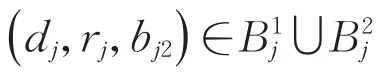
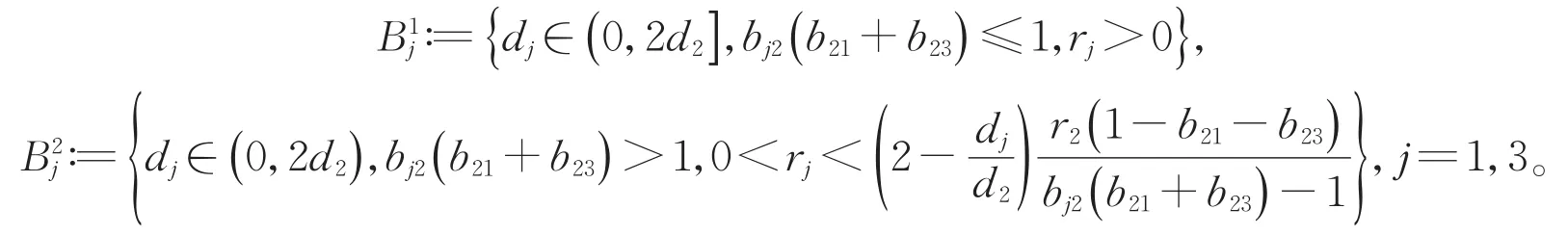
另外,Chang[11]利用单调动力系统理论和上下解方法给出了系统(2)波前解的存在性和指数稳定性。受文献[3]的启发,本文将利用上下解方法给出系统(2)最小波速的线性决定的充分条件,这个结果扩展了使得最小波速是线性决定的参数的取值范围。最后,在本文中,我们介绍R3中的序,即对于向量=(u1,u2,u3)和=(v1,v2,v3),如果 ui≤vi,i=1,2,3,那么如果并且至少有一个ui≠vi,i=1,2,3,那么
1 预备工作
这节我们将会给出系统(3)上下解的定义并介绍一些已知的结果。首先,我们给出系统(3)上下解的定义,为了方便,令
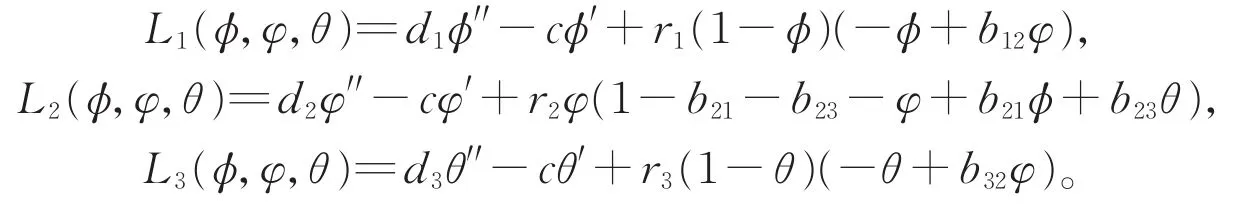
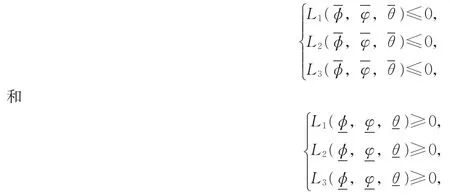
其次,由文献[3-4],我们归纳出下述引理。
2 线性决定的一般判别法则
在前一节的基础之上,本节,我们通过上下解方法建立系统(2)最小波速线性决定的一般判别法则。首先,我们介绍一个非自治系统解的存在性结果。
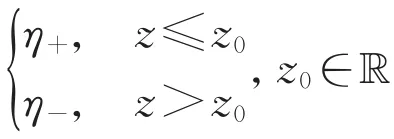
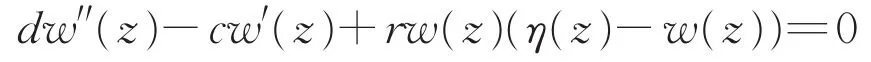
存在一个单调的解w(z)满足w(-∞)=η+,w(+∞)=0。
根据引理2,与文献[3]类似,我们可以进一步证明下述引理。
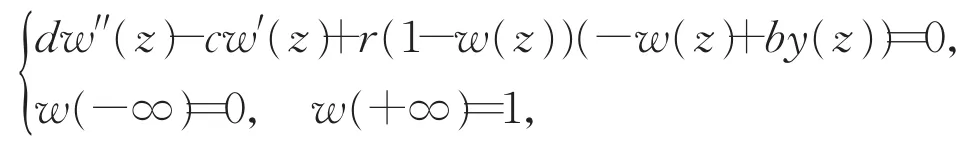
其中k为正常数,b>1。
其次,为了构造系统(3)的上下解,我们对(3)的第二个方程线性化得到如下的特征多项式
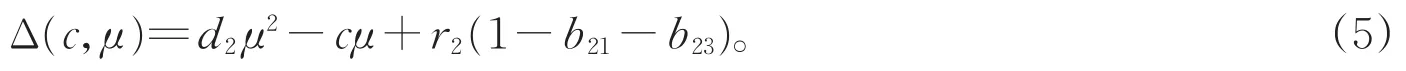
易证c>c0时Δ(c,μ)=0有两个正实根
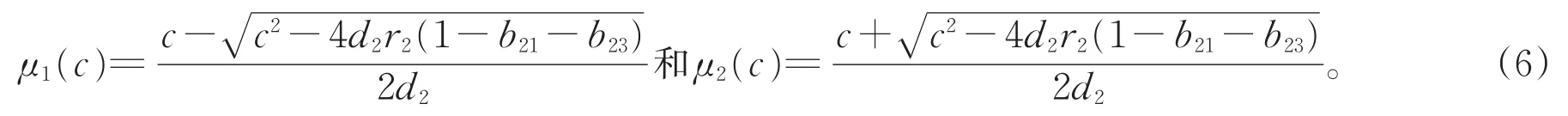
而当c=c0时,Δ(c,μ)=0有一个重根。在之后的证明中我们令c=c0+ε1,其中ε1>0充分小。我们接下来通过下述引理给出系统(3)的下解。
引理4 假设(H)成立。令
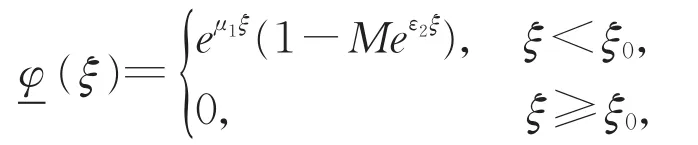
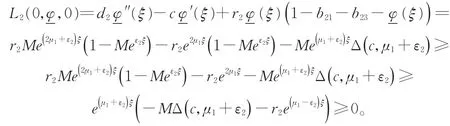
由文献[3]知,为了得到最小波速是线性决定的一般法则,我们需要构造合适的上解。令
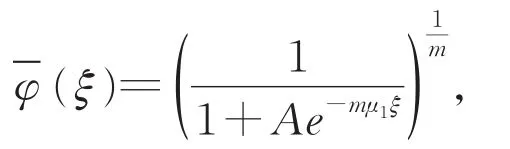
定理1 假设(H)成立。如果
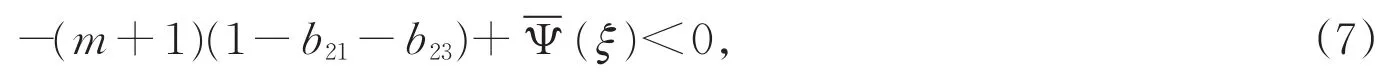
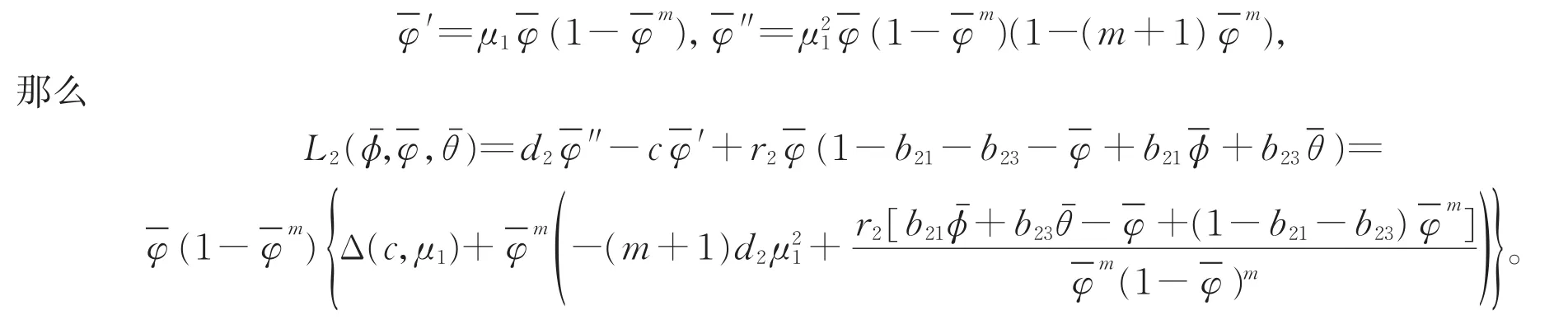
当ε1→0时,

3 精确的线性决定的充分条件
在本节,我们将在下面的定理中构造合适的上下解进一步给出精确的线性决定的充分条件。
定理2 假设(H)成立。如果
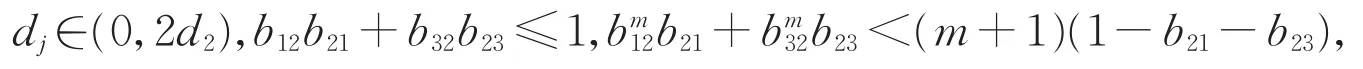
那么系统(2)的最小波速是线性决定的。
证明 令
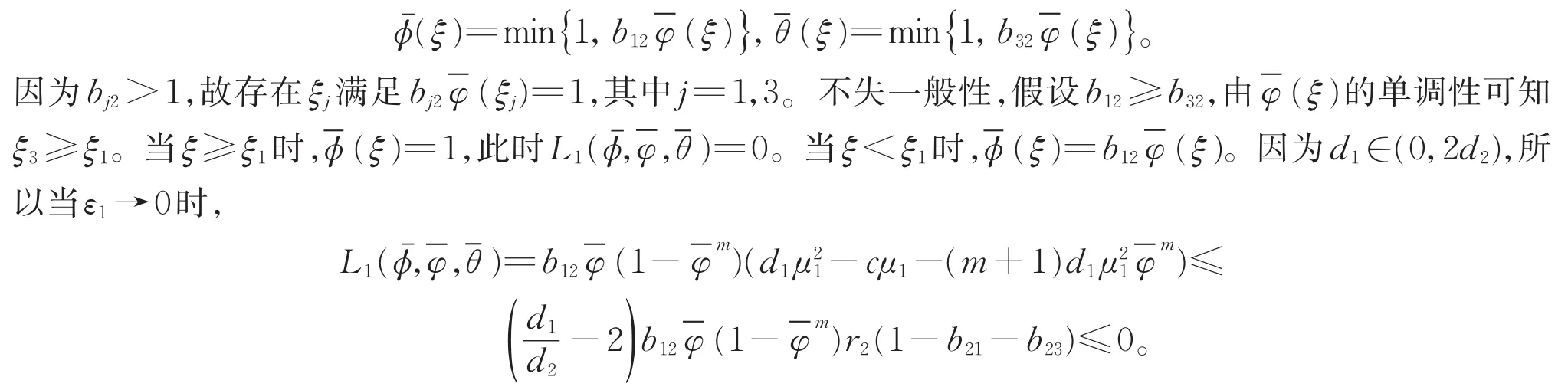
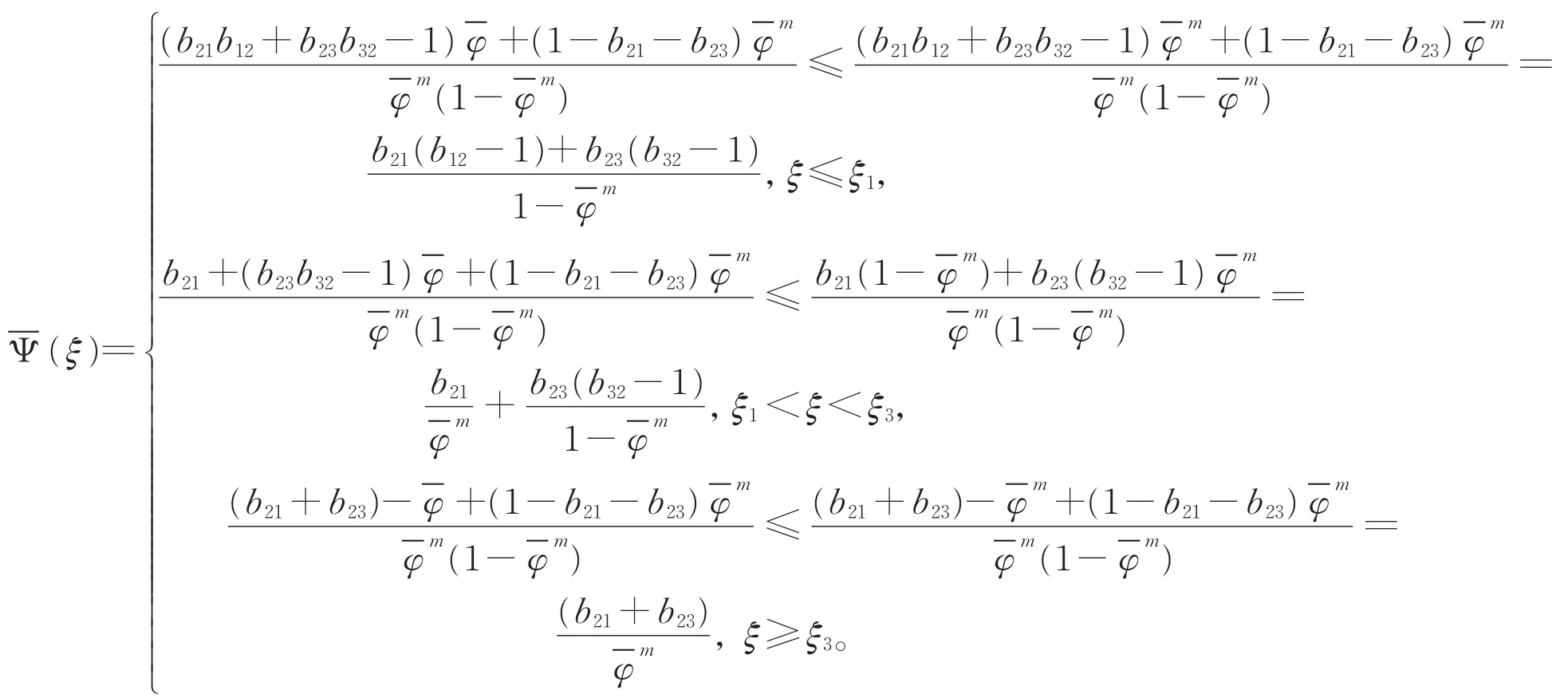
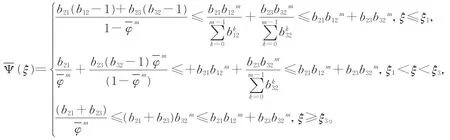
由条件可知-(m+1)(1-b21-b23)+(ξ)<0,定理得证。