基于图像表面形状指数的图像纹理特征提取

申 柯，陈 熙，张云飞

（贵州师范大学大数据与计算机科学学院，贵阳 550025）

0 引言

在计算机视觉中，我们一般通过分析图像纹理来获取相关的信息。像人的皮肤表面、材料表面、各种织物等都有其独特的纹理特征［1］。这些纹理特征已被广泛应用于生物特征识别［2］、医学图像分析［3］、遥感和视觉检测［4］等。纹理研究工作已经持续了几十年，但它对于我们来说仍然是一个难题，许多研究者通过不断的实验寻找更有效的纹理特征描述方法。

LBP［5］最初被提出用于纹理分析，它在计算复杂度和识别率方面表现出独特的优势。后来，在Ojala 等［5］的工作基础上，大量LBP 的变体被提出。Tan 等［6］基于LBP 提出了局部三值模式（local ternary pattern，LTP）用于人脸识别，该算法引入一个阈值函数，将原始LBP 扩展成三值编码。Hadizadeh［7］引入了Gabor滤波器，开发出了局部Gabor小波二元模式，实验验证它可以同时抵抗噪声和旋转的影响。近年来，随着深度学习的发展，人们提出了基于CNN 的纹理识别方法，但是需要大型的数据库才能够凸显其优势［8］。

上面提及的LBP 算法以及其改进算法在纹理识别方面取得了巨大的成功，但是仍然存在一些未解决的问题：①应对噪声影响，识别率过低的问题；②其旋转不变模式是离散的，不是连续的；③在准确性和效率之间进行权衡仍然是一个棘手的问题。因此，本文对这几个尚未解决的问题提出了相应的方案。

本文提出了一种新的混合特征的提取方案来改善这些缺陷，该方案通过引入添加了形状指数的LBP 描述符对局部凹凸模式方法进行补充。基于形状指数的LBP 描述符是一种高效的连续旋转不变描述符，形状指数由图像表面主曲率构造，它可以提取得到图像表面宏观和微观结构纹理信息，既保留了原始LBP 简单有效的特点，又引入了连续旋转不变性和高分辨率特性。所以，我们提出了一种更加鲁棒的SILCCP 的混合特征提取模式，通过融合图像表面纹理的结构信息和凹凸性两方面的特征对纹理进行分析，改善传统的特征提取方法。通过必要的理论分析以及大量的纹理识别实验研究，证明了我们提出的方法拥有良好的性能。

1 相关工作

1.1 LBP算法描述

LBP 是一种用来提取局部纹理特征的纹理描述符。原始的LBP 是一个强大的纹理描述符，它通过用中心值对每个像素的3×3 邻域进行阈值化来编码每个像素。对于一个3 × 3 局部区域，核函数的定义LBP算子如式（1）所示:

其中P为所涉及的邻域像素个数，R为中心像素gc周围的邻域半径，gP为其邻域像素的灰度值，S(x)为阈值函数，对S(x)的结果进行加权，得到一串二进制数。

随着采样点数量的增加，二值模式的数量将急剧增加，导致数据太多，直方图太稀疏，无法很好地反映图像特征。为了提高统计性能，提出了一种统一模式来降低LBP 算子模式类型的维数。表示为，如式（3）所示:

其中，U(LBPP,R)用于计算LBPP,R中“0/1”或“1/0”的转换。上标riu2 反映了使用不大于2 的U(LBPP,R)个值的旋转不变量的统一模式，所有其他情况都归因于P+1 个统一的二进制模式。均匀LBP 通过将2^P指数模式转换为P（P-1）+2个模式来减少内存占用，通过降低特征维数来减少高频噪声的影响。

1.2 LCCP算法描述

LCCP 及其扩展是一种性能优良的灰度和旋转不变的局部纹理描述子。Chen 等［9］提出了LCCP 以及LCCP 的相关扩展，并且实验证明了LCCP 以及其扩展在纹理识别上的独特优势，尤其是对光照的鲁棒性更强。图1 显示的是通过双线性插值的方式构造出新的采样点，得到了8个方向的凹凸信息构造8位LCCP模式。

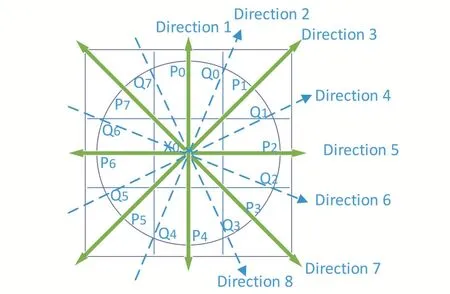
图1 插值后的LCCP信息

在图1 中，中心像素点X0的8 位LCCP 模式以式（5）表示：

1.3 主曲率

在微分几何中，主曲率作为分析局部纹理强度的基本属性，在描述目标图像的空间纹理结构时具有诸多优点。对于三维空间中可微曲面上任意一点P0点处的法向量是唯一的。在60点处有无穷多个包含法向量n的法平面。此外，有一对法平面可以使它们与曲面的交点在所有曲率中达到最大值或最小值。最小曲率表示P0点处弯曲程度最小的曲线，其曲率用λ1表示。垂直于最小曲率平面的曲率为最大曲率，用λ2表示，这两个曲率统称为主曲率。因此，主曲率能够准确地反映纹理图像的宏观和微观结构信息，而且无论图像以任何方向旋转任意角度，主曲率都能保持恒定，非常适合作为纹理分类的补充信息。图2为主曲率在局部图像表面的示意图。

图2 图像表面主曲率表示

2 相关方法

2.1 形状指数的构造方法

在微分几何中，主曲率可以由二阶微分运算得到，所以，我们通过计算Hessian 矩阵的特征值来求取图像的主曲率，从而构建形状指数。给定一个灰度图像I(x,y)，构建形状指数的过程如下所示：

步骤一：计算图像I(x,y)的二阶高斯导数Gxx，Gxy，Gyx，Gyy。

其中，

计算标准差σ的高斯算子如式（6）所示：

步骤二：构建标准差为σ的Hessian矩阵

其中，*为卷积操作。

步骤三：根据矩阵特征值的乘积等于这个矩阵的行列式(detH)，与矩阵特征值的和等于矩阵的迹(trH)列两个等式可以解出两个特征值λ1与λ2。

通过引入(λ-λ1)(λ-λ2)=0，可以简化特征值的求解运算，可以得到：

将式（7）代入式（8）中，即可得到最大和最小的两个特征值λmax和λmin。

步骤四：结合λmax和λmin构建形状指数，在二维图像上进行检测。得到形状指数的定义式如式（10）所示：

2.2 相似性度量

在纹理分类阶段，我们使用直方图交叉距离对得到的测试样本直方图和训练样本直方图进行相似性度量，直方图交叉距离可以快速地处理大量的数据，适用于灰度直方图之间的距离匹配。假设训练集图像I和测试集图P两幅图像特征分别为，然后计算识别成功率。其中直方图交叉距离公式如式（11）所示：

其中，Y表示融合子图像数量，Z表示所生成融合特征向量的长度。

2.3 算法流程

图3为本文的算法基本流程。首先对原始图像进行了分块处理。在后续实验中，需要分别对分块数为1 × 1、1 × 2、2 × 2、2 × 4、4 × 4的图片提取其小块的直方图进行计算，最后连接所有分块的直方图信息进行匹配，得到最优分块的识别性能。使用形状指数标记图像表面特征强度，对局部统一LBP的性能进行强化，使其获得连续旋转不变性。将强化的LBP 与噪声鲁棒的LCCP进行算法融合，提取图像纹理特征信息。提取特征直方图。将强化的LBP 特征直方图与LCCP 特征直方图进行融合，得到最终的特征向量。

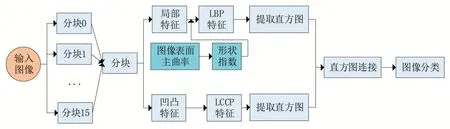
图3 算法流程图

3 实验结果与分析

在本小节中，我们对提出方法的性能进行多维度的分析，并与大量先进的纹理分类方法进行了全面的比较评估，验证了所提出方法在纹理识别上的优越性。为了验证SI-LCCP 描述符的优势，在四个具有挑战性的纹理数据库：CUReT 纹理数据库、ORL 人脸数据库、Extend Yale B 人脸数据集以及香港理工大学Poly U 掌纹图像数据集上进行了图像分块与分类实验，与现阶段最先进的算法进行比较，验证了算法在应对旋转不变性方面具有独特优势。为了验证算法应对噪声的有效性，还对噪声环境下的图像进行实验。

3.1 数据集及实验设置

ORL 人脸数据集是由英国剑桥的Olivetti 研究实验室创建的。包含400 张图像，其中包括40 个人，每人10 张在不同的时间、不同的光照、不同的面部表情和面部细节环境下采集的，是人脸识别常用的数据集之一。图4（a）是该数据集中截取的图片样本。图4（b）截取的是Yale大学创建的Extend Yale B 人脸数据集，该数据集包括38个人，每人64张，共2432张在不同光照、不同表情和不同姿态下的人脸图像，是一个非常有挑战性的光照变化的数据集。图4（c）是从香港理工大学Poly U 掌纹图像数据集中截取的图像，数据库包含7752 幅BMP 图像格式的灰度图像，对应386个人不同的掌纹。该数据集中所有原始掌纹图像的分辨率为384 × 284 像素。我们选取其中100 个人，每人6 张掌纹图像进行实验验证。

CUReT 纹理数据集是一个具有挑战性的纹理识别数据集，它包含61 个类，每个类中包含205幅不同视角、尺度与光照下拍摄的图片，有较大的类内差异。我们随机选择其中48 幅图像进行实验，选取N张图像作为训练数据，剩余作为测试数据。图4（d）是数据集中选取的部分图像样本。

图4 预处理样本图像

3.2 不同分块下的实验性能

图像分块对于实验识别效果有着很大的关系，分块过少可能会导致提取特征过少，而分块过多可能导致噪声的影响扩大。实验中，我们在每个数据集中随机选取样本数的一半作为训练数据，剩余数据作为测试数据进行实验验证，为了保证随机选取数据的有效性，我们每轮重复进行10 次实验求取其平均值。从表1 的数据结果可以看出：ORL 数据集上在2 × 2 分块时达到最佳的识别效果，分块越多，其识别率会越低，在Extend Yale B 数据集上我们可以看出分块越多，其提取的特征越细，识别效果越好。在Poly U 数据集上，在4 × 4 分块的时候识别效果达到最佳。

表1 不同分块下的平均识别率与标准偏差 单位：%

3.3 旋转不变性验证

CUReT 数据集包含了不同角度旋转的图像，存在显著的视点、光照和旋转的变化，并且具有较大的类内差异，我们可以使用它来验证融合形状指数的算法在克服旋转不变性等方面的独特优势。为了得到更可靠的实验结果，在CUReT 数据集上所有的实验均进行了10 次并且最终结果以平均识别率为准。同时证明本方法的有效性，在表2中与最新的研究成果以及非常经典的方法进行了综合比较。

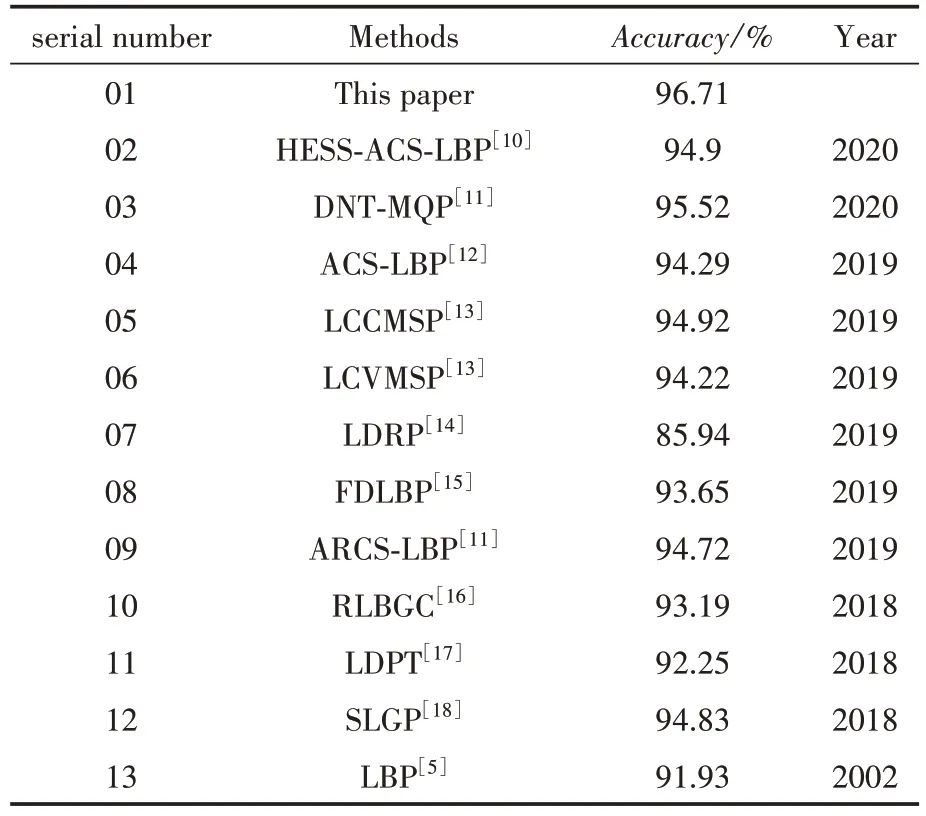
表2 不同方法在CUReT数据集上的结果

通过与现阶段先进方法的比较，本文算法在极具挑战性的CUReT 数据集上取得了很好的效果，虽然数据集包含了许多旋转、光照、视点等图像，提出的方法都能有效面对。由此可见，本方法在一些变化比较小的数据集上也能提供稳定的性能。

3.4 不同噪声环境下的性能

为了评估本文算法在噪声环境下的性能，我们给Extend Yale B 中的数据添加了不同种类的噪声进行实验验证，并与经典的同类型算法以及融合形状指数之前的算法进行比较，并且将噪声鲁棒性很好的CS-LDP［19］加入到此次实验。通过人为给图像添加噪声可以使得原本较高的识别率下降，因此，通过在添加噪声环境下依旧能够保持相对较高的识别率来说明该算法对噪声具有鲁棒性。

这一部分在Extend Yale B 数据集中进行实验。实验中在随机选取的训练样本上使用函数imnoise（Train_im，‘salt &pepper’，0.2）来添加椒盐噪声和使用imnoise（Train_im，‘poisson’）添加泊松噪声。每类图像随机选取n个样本作为训练集，剩余（64 -n）个样本则作为测试数据（不进行添加噪声）进行实验。重复10 次实验计算其平均识别率，实验结果记录在表3中。

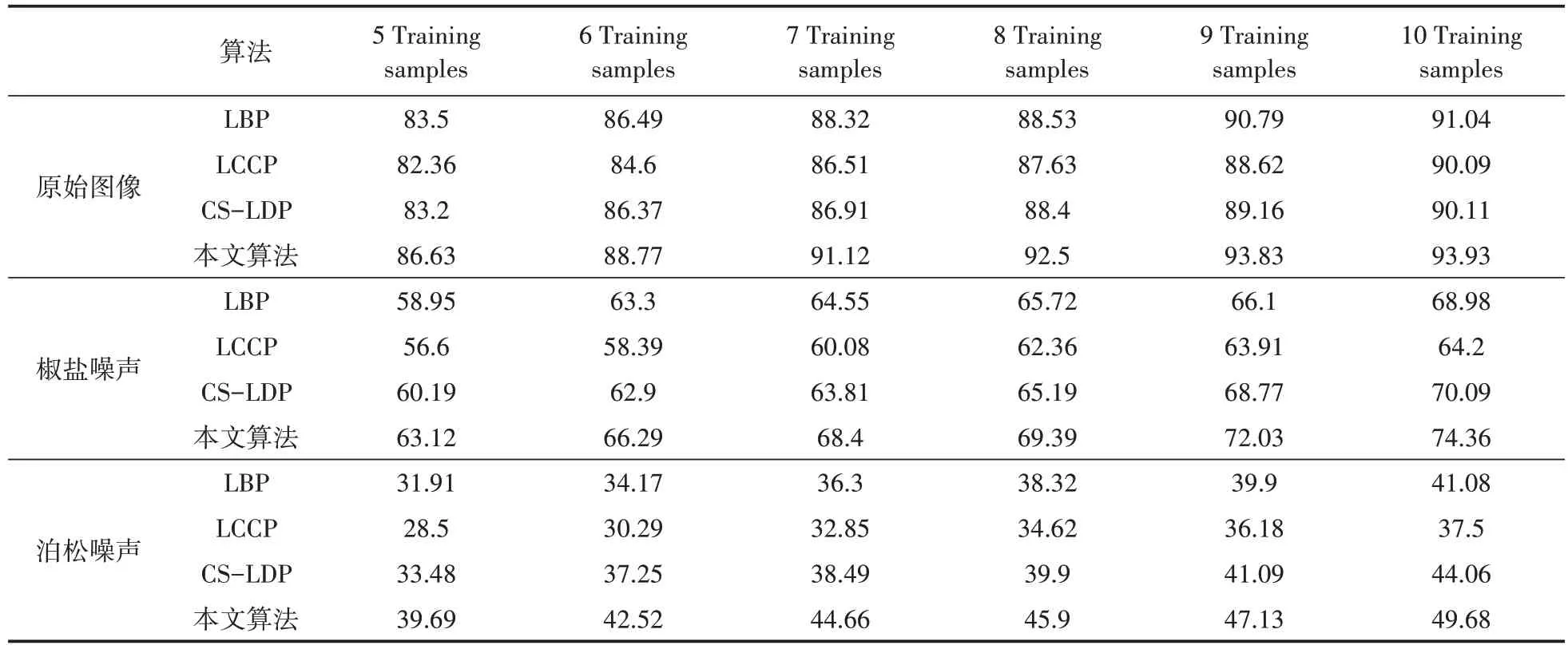
表3 在Extend Yale B数据集中图像加入噪声情况下各算法的平均识别率 单位：%

4 结语

本文利用图像表面形状指数连续旋转不变的特性，提出了一种有效的特征描述算子用于纹理分类。形状指数基于主曲率构造，主曲率能够准确地反映纹理图像的宏观和微观结构信息，无论图像以任何方向旋转任意角度，主曲率都能保持恒定。通过跟多种方法比较，结果证明了形状指数的该特性有效改善了原来局部算法的旋转不变性。并且将另一种局部凹凸模式LCCP 算法进行了融合，使得提取的纹理信息包含了图像表面凹凸信息，在应对噪声方面获得了更好的效果。我们分别添加两种不同噪声进行测试，本文算法对添加两种噪声的数据均获得了更高的识别性能，证明了其应对噪声的鲁棒性。在未来，希望能够更深地挖掘图像形状指数的其他信息，希望其能够对纹理识别与分类的研究提供新的思路。