GOCE引力梯度内部校准方法

潘娟霞，邹贤才,2

1. 武汉大学测绘学院，湖北 武汉 430079； 2. 武汉大学地球空间环境与大地测量教育部重点实验室，湖北 武汉 430079

重力测量卫星GOCE(gravity field and steady-state ocean circulation explorer)是由欧空局(European Space Agency，ESA)研制和发射的低轨重力探测卫星，其科学目标是在100 km的空间分辨率内(即恢复200阶次以上的全球重力场模型)以2 cm的精度测定全球大地水准面及10-5m/s2的精度测定重力异常。相比CHAMP(challenging minisatellite payload)和GRACE(gravity recovery and climate experiment)卫星，GOCE关键载荷是一台高精度的引力梯度仪，由6个加速度计对称安置在3个正交轴上，3对加速度计基线长约50 cm，卫星质心与梯度仪质心重合，从而利用加速度计差分观测值直接测定引力位的二阶梯度张量，并以加速度计共模观测值获得作用于卫星的非保守力[1]。GOCE还有精确的高低卫星跟踪数据及无阻尼控制，联合引力梯度数据及高低卫星跟踪数据解算重力场是其独特优势。

GOCE引力梯度仪受到测量误差、外界观测条件等因素影响，导致观测值出现系统偏差、比例误差及有色噪声等，因此，反演重力场前针对GOCE观测数据的校准至关重要。安装结构不同导致GRACE卫星的加速度计校准方式不再适用于GOCE。国内外诸多学者针对GOCE数据的使用及校准做了大量研究，通常根据是否引入参考重力场模型等外部辅助数据将GOCE的校准分为内部校准及外部校准，校准模型通常包括比例因子、偏差因子。文献[2—3]提出用恒星敏感器测量数据及先验重力场估计比例因子，该模型还校准了梯度仪坐标系(gradiometer reference frame，GRF)与恒星敏感器坐标系(star sensor reference frame，SSRF)间未配准的问题。文献[4]提出了将恒星敏感器联合梯度仪测量数据重建的卫星角速度用于校准模型中。文献[5—6]提出类似方法用恒星敏感器数据及加速度计测量值进行内部校准，并针对观测值时间相关性提出解决方案，该方法即为ESA官方采用方法。文献[7—8]根据精密轨道确定比例因子与偏差因子，利用恒星敏感器数据对校准后的引力梯度数据进行验证。文献[9—10]发现在校准模型中加入二次因子可以减弱地磁极周围强风的影响，于2018年引入外部重力场模型对GOCE数据重新处理。国内诸多研究包括对GOCE卫星数据的预处理研究、梯度数据确定地球重力场的理论方法研究[11-13]及基于加速度计数据的校准方法研究，文献[14—16]提出联合几何法精密轨道以动力法完成单加速度计校准及卫星非保守力确定，同时解算重力场模型和校准参数，从而降低参考重力场模型误差对校准结果的影响，并讨论了卫星无阻尼控制的补偿效果。文献[17]利用外部重力场及恒星敏感器数据初步验证对一定频段内校准的有效性。文献[18]讨论利用不同外部重力场模型校准及相同重力场模型不同阶次对校准结果的影响。

目前，国内针对GOCE数据的处理及使用以ESA内部校准后的数据为主，本文以ESA官方发布的方法为基础，实现GOCE数据的内部校准，主要目的是为完善GOCE梯度仪观测数据的校准处理，并为讨论内部校准、外部校准方法及动力法校准的联合、比较做初步准备。ESA发布的内部校准方法将误差因素模型化为3个加速度计对的逆校准矩阵，并将该矩阵作用于加速度计实现校准，本文在此基础上提出了顾及SSRF与GRF间的旋转矩阵的校准参数的改进模型，讨论这一变化对卫星引力梯度精度带来的改变。涉及的数据包括卫星搭载的梯度仪及恒星敏感器测量数据，利用加速度计共模观测值及差分观测值与恒星敏感器的姿态数据，根据卫星引力梯度测量原理建立校准模型，以获取校准后梯度仪坐标系下的引力梯度。除此以外，恢复重力场还涉及梯度仪坐标系与惯性系的高精度转换，因此本文提出了关于卫星姿态重建的讨论。

1 理论与方法

1.1 内部校准

GOCE卫星上搭载了几类重要载荷，本文重点关注用于确定中短波重力场的静电引力梯度仪(electrostatic gravity gradiometer，EGG)，以及提供卫星姿态的3个恒星敏感器。GOCE是第一颗采用无阻尼控制技术的卫星，沿轨方向大气阻力得到持续补偿。卫星实际运行过程中，存在诸多误差因素，为此GOCE设计了每两个月执行一次特定的持续1 d的振动，用于卫星的校准，该振动期间的数据称为shaking数据，其他时段称为nominal数据。图1为梯度仪坐标系中3对加速度计安置结构，实线代表超敏感轴，虚线代表非敏感轴[6]。

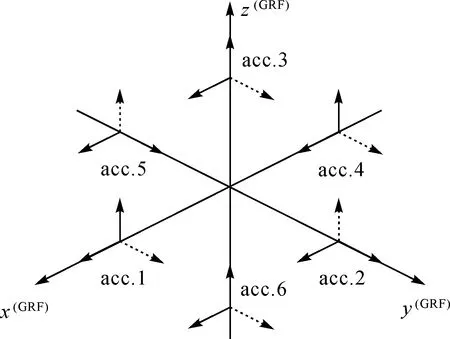
图1 梯度仪坐标系中3对加速度计安置结构Fig.1 Arrangement of the three pairs of accelerometers in the GRF

1.1.1 共模加速度与差分加速度

图2是梯度仪中3对加速度计的特殊结构，根据卫星引力梯度测量原理，第i个加速度计测得的加速度值为

(1)

梯度仪两类观测模式为差分模式加速度(differential mode acceleration，DM)与共模加速度(common mode acceleration，CM)[6]

(2)

(3)

ac,ij≈d

(4)

(5)

式(5)表达为矩阵形式

(6)

式中，Ad=(ad,14,ad,25,ad,36)，而矩阵L[6]

(7)

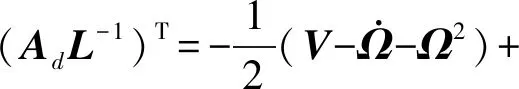
(8)

AdL-1+(AdL-1)T=-V+Ω2

(9)

1.1.2 校准模型

卫星实际运行过程中，通常考虑以下误差因素：①加速度计质心偏离标称位置；②加速度计各坐标轴未严格与梯度仪相应坐标轴对齐；③加速度计3轴不完全正交；④由于数据输出增益的不确定性，产生的加速度计比例因子[10]。将误差参数化为比例因子、偏差因子及二次项，其中二次项以物理振动的方式予以消除[19]，因此内部校准矩阵应包括比例因子与偏差因子。图3表示除非线性二次项以外的加速度计误差因素，每个加速度计包括6个角度校准参数、3个比例因子，6个加速度计共需要确定54个校准参数，定义校准矩阵[6]

(10)

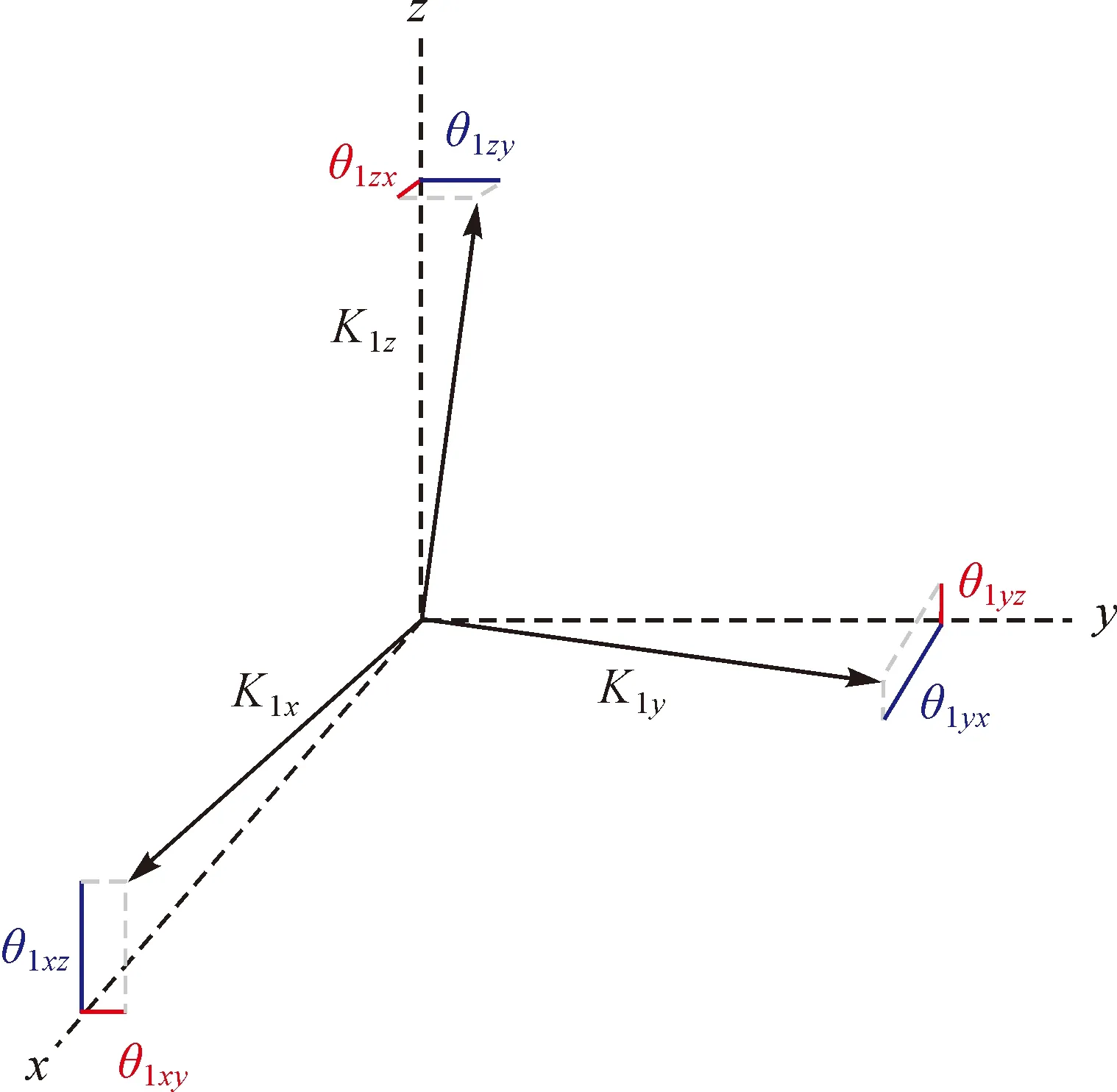
图2 单个加速度计的误差来源Fig.2 Error sources of a single accelerometer

(11)

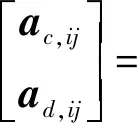
(12)

式(12)给出了测量值、真实值及逆校准矩阵间的关系。

式(4)表示由3对加速度计观测值给出的共模加速度CM即是卫星在3个方向所受到的非保守力，有以下6个独立条件

E{ac,ij-ac,kl}=0ij=14,25,36,ij≠kl

(13)

(14)

类似地，联合恒星敏感器角速度ΩS，式(9)可变换为

(15)

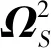
图3 0.05～0.1 Hz内离心加速度、差分加速度、引力梯度PSD1/2比较Fig.3 Comparison of PSD1/2 of centrifugal acceleration, differential acceleration and gravity gradients in the 0.05～0.1 Hz

(16)

根据式(13)、式(14)与式(16)，以ESA官方发布的卫星nominal时段的梯度仪测量数据EGG_NOM_L1b及恒星敏感器数据STR_VC2_1b与STR_VC3_1b作为输入数据以实现内部校准。

建立以上模型时，做了以下假定：①ESA给定的引力梯度仪基线长Lx、Ly、Lz是准确且为固定常数；②ESA给定的SSRF与GRF间的相对关系是准确且为常数矩阵；本文探索考虑这两个假定是否准确以及其对引力梯度精度的影响，在基础模型上加上新的参数重新建立模型。用微小旋转角rx、ry、rz描述恒星敏感器与梯度仪坐标系间旋转矩阵随时间的变化对角加速度的综合影响，用GRF′表示标称梯度仪坐标系，GRF表示存在偏差的坐标系，两坐标系中角加速度的关系表达为

(17)

(18)

(19)

写成分量形式为

(20)

由于式(17)在0.05～0.1 Hz频段内作了近似处理，且分母上省略了基线长Lx、Ly、Lz，导致基线长的估计少了完整约束，因此本文暂不讨论基线长随时间的变化，仍然认为其数值为常数。本文在ESA方法的基础上，利用式(13)、式(20)及式(16)完成内部校准。

1.1.3 协方差矩阵处理

本文采用2 d的数据估计一组校准参数，根据GOCE采样率及有色噪声的特点，难以实现矩阵的存储与求逆运算，参考文献[6,10]，利用对称的滑动平均去相关滤波，实现去相关处理的同时实现相应频段滤波，避免大型矩阵的求逆，式(21)为去相关滤波表达式

(21)

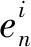
1.2 恒星敏感器的联合

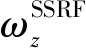
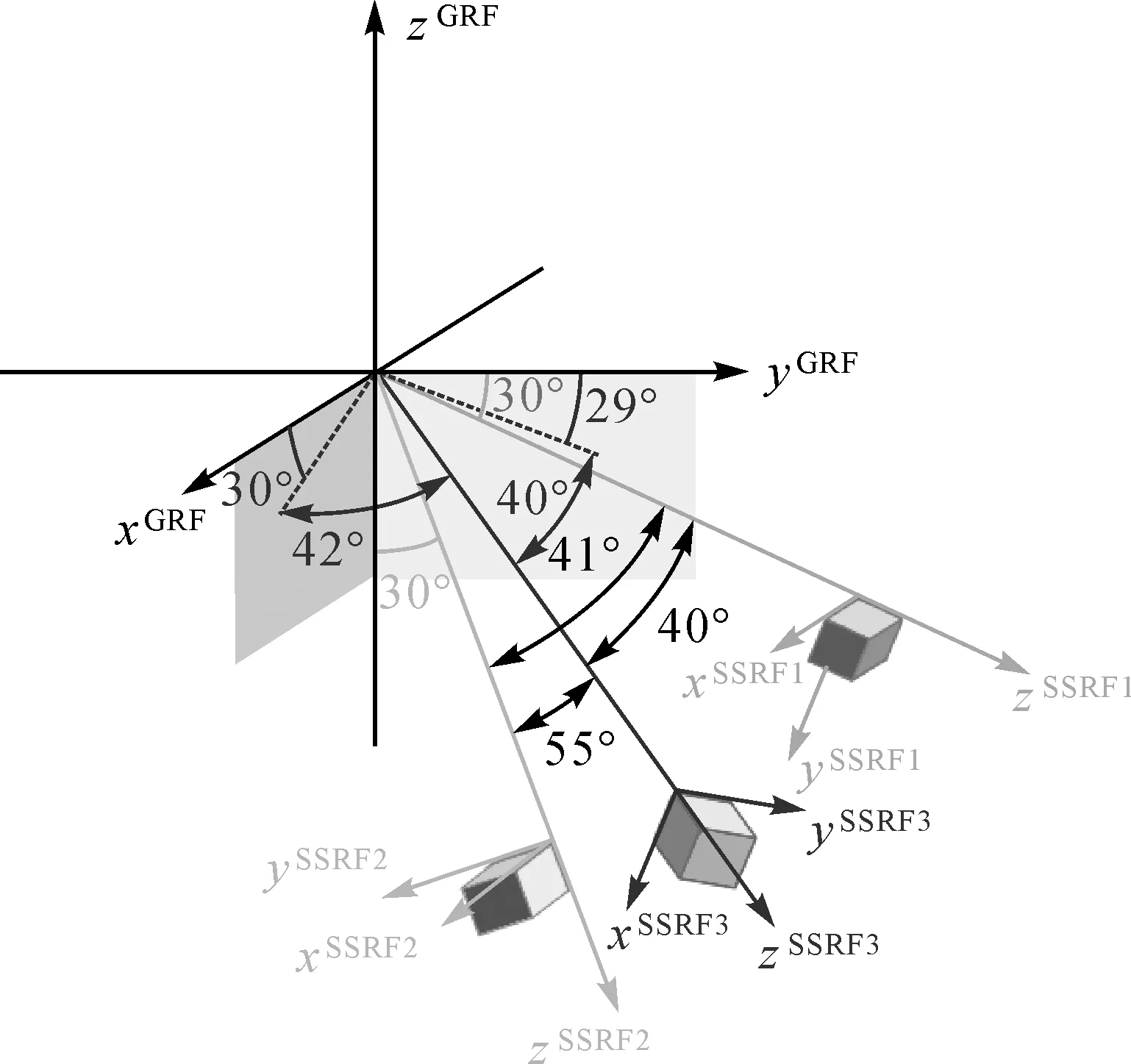
图4 梯度仪坐标系与3个星敏感器坐标系的相对关系[6]Fig.4 Relative orientation of the GRF and the SSRFs

1.3 角速度与姿态重建

角速度与姿态四元数的精度直接影响到引力梯度与地球重力场反演精度，对角速度及姿态的重建是必要的。恒星敏感器观测的四元数变换到角速度需经过数值微分的过程，导致高频段噪声被放大，加速度计观测值经积分导出的角速度及四元数则放大了低频噪声。文献[19]采用卡尔曼滤波实现角速度与姿态重建。文献[20]利用恒星敏感器角速度与梯度仪角速度建立频域内的权重模型，以维纳滤波重建角速度与姿态。文献[10]提出采用最小二乘拟合以重建姿态。卡尔曼滤波与最小二乘拟合均在时域内展开而未使用频域特点，且卡尔曼滤波的瞬态效应严重造成数据利用率不高，本文参考[20]利用维纳滤波在频域内联合两类数据的优点实现角速度及姿态重建。

维纳滤波的原理是根据两类观测值精度实现频域内的加权平均，频域内某频率的功率谱密度值(power spectral density,PSD)代表该处的精度

(22)

式中，HSTR(f)与HGRAD(f)分别代表敏感器与梯度仪的权重；PSTR(f)、PGRAD(f)分别表示频域内两类角速度的平方根功率谱密度，模型参考文献[20]。图5为两类角速度噪声PSD1/2，其中，G代表梯度仪，S代表恒星敏感器。

图5 两类角速度噪声PSD1/2Fig.5 PSD1/2 of two types of noise

角速度最终通过频域内乘积与傅里叶正反变换计算得到

(23)

(24)

式中，t代表观测时刻。

2 数据分析

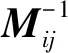
图6 部分参数序列Fig.6 Part parameters series of

图7 校准后引力梯度张量迹的PSD1/2Fig.7 PSD1/2 of calibrated gravity gradient trace

表1 加速度计对比例因子Tab.1 Scale factors of accelerometer pairs

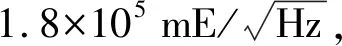
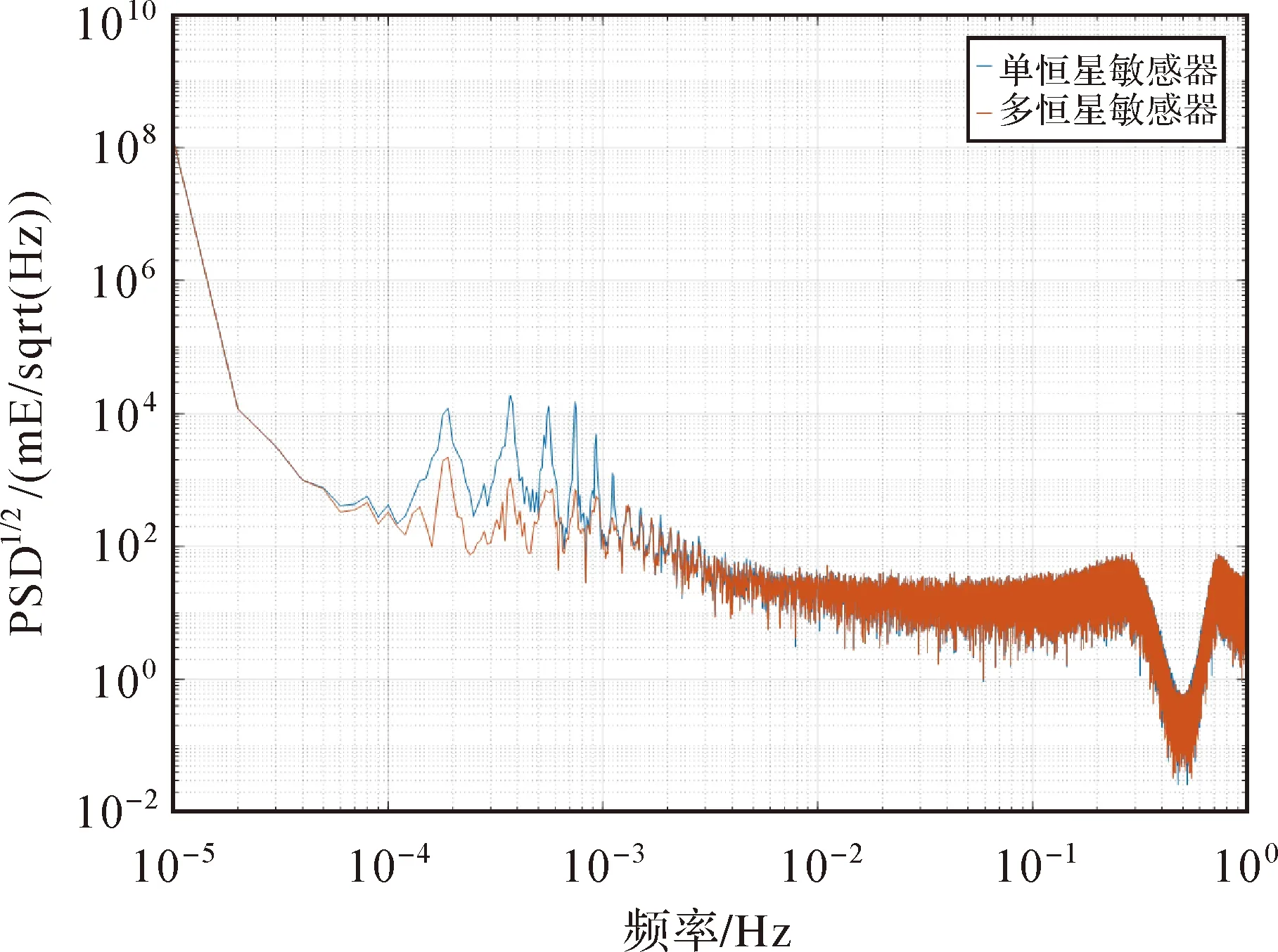
图8 恒星敏感器联合前后引力梯度张量迹的PSD1/2Fig.8 PSD1/2 of calibrated gravity gradient trace before and after combination of star sensors

图9 恒星敏感器联合前后对应引力梯度分量与模型参考值差值的PSD1/2Fig.9 PSD1/2 of differences of gravity gradients to EIGEN-5C model before and after combination of star sensors

在第1类ESA模型基础上，本文增加了SSRF与GRF之间旋转矩阵随时间变化的参数ΔR，这一变化将对角速度及姿态重建过程产生影响，引力梯度分量也将产生相应改变。这里给出新增参数ΔR的数据序列及线性拟合序列，图10中存在几个明显异常值，分析相应时间段内3个恒星敏感器工作状态，统计发现在异常值存在的时段内，仅有单个恒星敏感器数据可用的时刻数远大于其他时段相应值，这也体现了联合多个恒星敏感器的优势和必要性。rx、ry、rz数值绝对值在100″左右且该月数值呈现约3～30″的线性趋势，因而建立校准模型时该校准参数不应被忽略。

图10 参数ΔR序列Fig.10 Time series of ΔR

将ΔR作用到恒星敏感器角速度及四元数，再重建角速度与姿态以定量分析新增校准参数对引力梯度精度的影响。图11给出了加入参数ΔR前后引力梯度分量与参考模型引力梯度差值的平方根功率谱分析，表2为低于0.005 Hz频率的两类校准模型对应引力梯度分量与模型参考值差值的平方根功率谱统计结果，其中“方法1”表示与ESA模型一致，“方法2”代表新增ΔR的结果，4个引力梯度分量Vxx、Vxz、Vyy、Vzz对应的差值平方根功率谱均显示增加新的参数后引力梯度分量的精度有一定提升，其中分量Vxz精度提升最大，这是由于“方法2”中新增的参数改变了卫星的姿态，相对其他分量而言，Vxz分量对姿态的变化更敏感，从而其精度提升最大。由于新增参数主要影响到姿态四元数，而梯度张量迹不会随四元数改变[21-27]，这里未提供相应对比图。

图11 两类校准模型对应引力梯度分量与模型参考值差值的PSD1/2Fig.11 PSD1/2 of differences of gravity gradients to EIGEN-5C model for the two calibration models

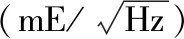
表2 两类引力梯度分量与模型参考值差值的PSD1/2统计Tab.2 PSD1/2 statistics of differences of gravity gradients to EIGEN-5C model for the two calibration models

3 结论与展望

本文从GOCE卫星引力梯度测量原理着手，利用L1b数据中nominal时段的引力梯度仪观测数据及恒星敏感器姿态数据对加速度计测量值做内部校准，以最小二乘联合多个恒星敏感器观测值以避免SSRF及GRF间转换导致的误差传播；为得到惯性坐标系下更为精确的引力梯度张量以恢复重力场，采用维纳滤波重建了卫星角速度及姿态四元数。在ESA校准方法的基础上，提出顾及SSRF与GRF间旋转矩阵校准参数的内部校准模型，结果表明该组校准参数的数值绝对值在100″左右，且在该月呈现约3～30″的线性趋势，同时解算逆校准矩阵及SSRF与GRF间旋转矩阵校准参数的内部校准模型可改进低于0.005 Hz频段内引力梯度各分量的精度，对于梯度分量Vxz改进最大，证实了这一校准参数存在的必要性，对GOCE自身数据处理及后续重力卫星数据处理带来一定的参考价值。

最后在本文的基础上提出关于GOCE数据处理可能的改进方向：①由于无外部数据的约束，内部校准方法不能避免GOCE自身系统偏差造成的影响，因此考虑比较外部校准方法及动力法以联合各方法的优势，可推动梯度数据处理问题的讨论；②关于基线长Lx、Ly、Lz及ΔR的确定及二次项K2的补偿，考虑引入先验重力场并联合恒星敏感器数据解算；③在对协方差矩阵进行对称滑动平均去相关滤波过程中，本文统一选择滤波器阶数等于轨道周期长度，但实际解算时该长度估计的功率谱并不是最优，针对去相关过程中功率谱分辨率及精度的折中选择值得深入讨论。