建筑物形状特征分析表达与自适应化简方法

晏雄锋，袁 拓，杨 敏，孔 博，刘鹏程

1. 同济大学测绘与地理信息学院，上海 200092； 2. 武汉大学资源与环境科学学院，湖北 武汉 430079； 3. 华中师范大学城市与环境科学学院，湖北 武汉 430079

化简是矢量建筑物数据处理的基础性操作之一，其目的在于移除建筑物边界上的凹凸细节特征，从而满足制图表达的要求。在制图综合领域形状化简是建筑物尺度变换的主要算子之一，广泛应用于多比例尺地形图缩编、三维城市建模、导航地图生成与更新等诸多应用[1]。此外，该变换操作也是影像数据提取矢量建筑物的后处理环节之一[2]。从遥感影像中提取的建筑物轮廓通常难以直接用于制图表达，存在弱直角和冗余点等问题，需要运用化简方法进行去噪和规则化处理。

建筑物化简过程不仅需要控制位置偏移，而且要尽量保持目标原有的形状、大小、方向及正交性特征。对此，学者们设计了不同类型的建筑物化简算法。第一类算法注重局部特征的探测与简化处理，包括短边剔除法[3-4]、凹凸特征探测与渐进式删除法[5-7]、邻近四点法[8]等，还引入最小二乘[9-11]、整数规划[12]等优化技术提升短边或者局部凹凸特征处理的合理性。第二类算法强调建筑物化简前后整体结构的保持，包括迭代法[13]和模板匹配法[14-15]，主要面向具有特殊形状的建筑物目标。此外，一些学者借助数学形态学[16-17]以及图像处理技术[18-19]设计建筑物化简方法。上述算法设计的角度或采用的策略不同，面向不同形状的建筑物具有各自的适应范围和局限性。由于同一区域建筑物在几何形态上往往存在多样性，单一算法难以合理地化简所有建筑物目标。

破解上述难题的思路之一是将不同算法集成形成组合式化简模型[20-22]，使得每个建筑物目标能够依据自身形状特点自适应匹配适宜的化简算法。文献[21]较早开展相关研究，通过几何特征分析识别规则形状和不规则形状的建筑物，分别采用矩形拟合、直角化处理、短边剔除等不同化简操作，能较好地保持局部结构模式，但缺乏整体结构上的分析视角。文献[22]提出一种基于评价策略的混合式化简方法，根据化简前后位置、方向、面积、形状等指标变化从多种算法产生的候选方案中挑选最佳化简结果。该方法以结果为导向能够相对平衡地考虑多种化简指标要求，但是缺乏对形状特征的深层次认知。为此，本文提出一种深度学习支持下的形状自适应建筑物化简方法。该方法建立在对建筑物形状的整体结构认知和表达上，主要包括两个步骤：①构建一种基于图结构的卷积自编码网络，提取隐含在边界节点分布上的形状特征，并将建筑物形状表达为一组特征向量，从而实现对建筑物的形状特征表达；②采用机器学习分类的方法，在有监督的学习训练下建立形状编码与不同化简算法之间的映射关系，从而实现依据输入建筑物的形状特征选择适宜化简算法的自适应机制。

1 图卷积学习支持下的建筑物形状特征表达

建筑物的形状特征表达是化简动作实施的基础，主要包括两个部分：建筑物图结构构建及特征提取与建筑物形状的自编码学习模型。

1.1 建筑物图结构构建及特征提取

图是一种表达对象及其关联关系的数据结构，定义为G=(V,E,W)，其中节点集合V={v1,v2,…,vn}表示对象，E为连接节点的边集合，W记录边的权值。每个图节点可包含p个描述特征，构成特征矩阵f∈Rn×p。对于建筑物多边形的图表达，可将边界节点作为图节点，边界直线段对应连接图节点的边[23]。考虑到建筑物边界序列中间隔很远的节点也可能位置接近而存在视觉联系，本文采用Delaunay三角网建立边界节点间的空间邻近关系，将建筑物多边形内部三角形边作为图的连接边，如图1所示。

图1 建筑物边界预处理与图结构表达Fig.1 Preprocessing and graph-based representation for building boundary

不同建筑物间的节点数量和密度可能存在差异，因此需要进行冗余点剔除和内插加密预处理，以保证边界节点分布均衡性以及数量一致性。冗余点剔除主要目的是去除分布密集且对建筑物形状结构贡献度低的节点，采用Douglas-Peucker(DP)算法完成。其中，DP算法设置的矢高阈值需十分保守(例如0.01～0.05 m，以保证不能丢失关键的形状特征点。加密处理采用弧段内均匀插值方法，使得内插后节点数量达到预设固定值，该值依据剔除冗余点后建筑物节点的数量分布以及模型中特征图数量和池化层数，本文设为64。

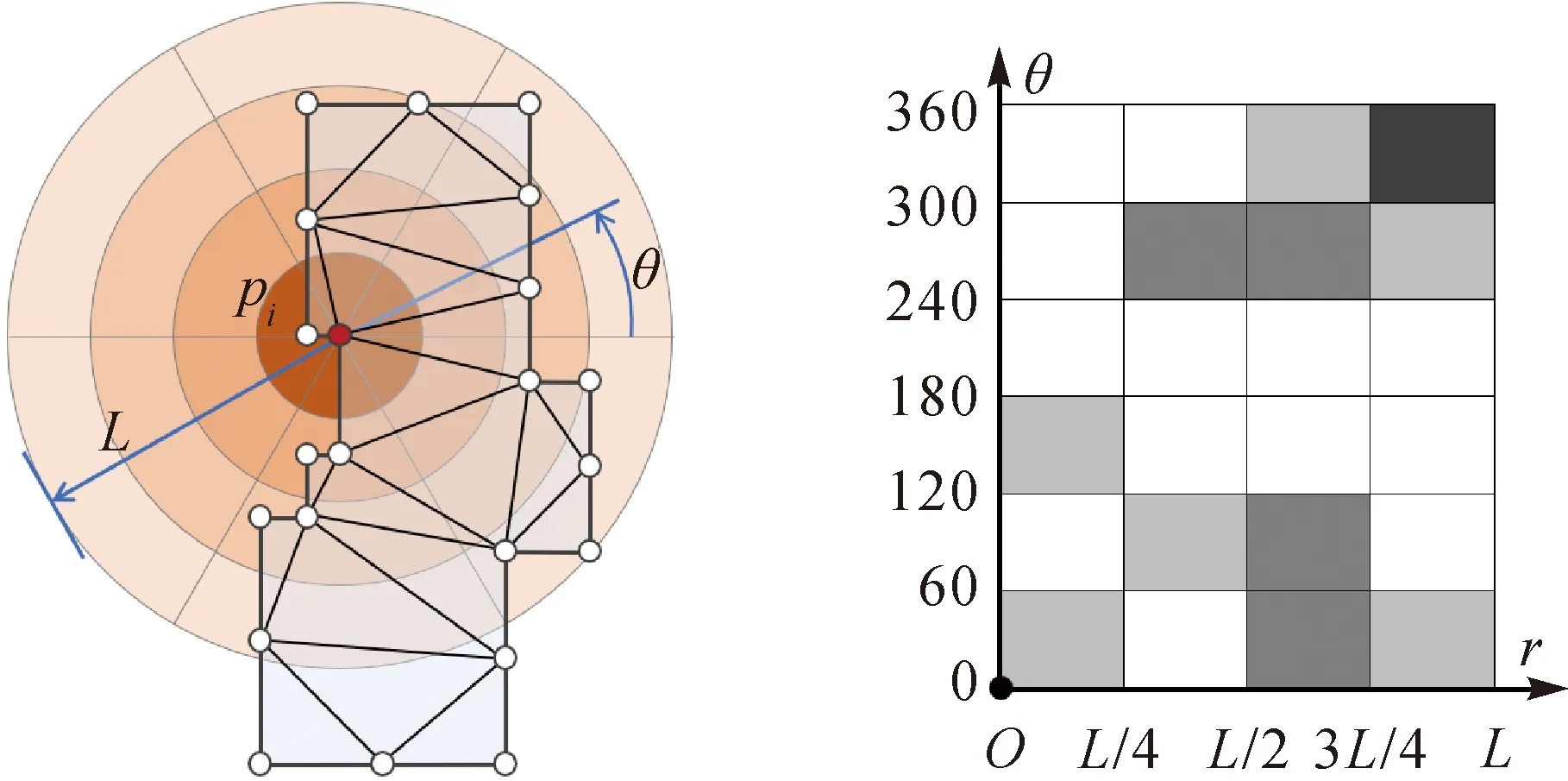
图2 建筑物边界节点的上下文特征提取Fig.2 Feature extraction of building boundary nodes using shape context descriptor

1.2 建筑物形状特征表达的图卷积自编码模型

本文参考U-net架构[24]，设计一种图的自编码学习模型分析上述构建的建筑物图结构，输入即邻接矩阵W64×64和节点特征f64×24。模型由编码器(encoder)和解码器(decoder)组成。其中，编码器包含一个卷积层和两个池化层，将输入的64×24维的建筑物形状特征编码为32维向量。解码器则由两个上采样层和一个卷积层构成，将32维编码向量恢复原始尺寸和特征维度。由于编码过程中压缩和提取特征减小了节点尺寸，可能会丢失空间位置信息。因此，解码过程中每次上采样操作后，将输出结果与编码时对应特征图进行连接增强运算。总体架构如图3所示。

图3 面向建筑物形状特征分析的自编码学习模型Fig.3 Graph-based autoencoding architecture for building shape representation

由于图上节点的邻域结构不固定，无法直接执行规范栅格上的卷积和池化等运算算子。本文介绍一种基于图傅里叶变换的卷积运算算子用于图上局部范围内用于特征提取，并在此基础上设计有效的池化和上采样运算。详细运算算子和损失函数介绍如下。

1.2.1 卷积运算

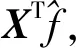
(XTg))。

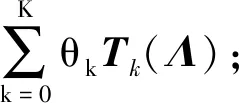
(1)

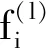
1.2.2 池化和上采样运算

图卷积本质上是利用拉普拉斯矩阵将图的节点特征矩阵fn×Fin映射到fn×Fout。该过程更新图的节点特征，但不会改变图的尺寸，因此不利于层次化特征的提取以及数据表征维度的改变。针对此，本文采用DIFFPOOL方法[26]，即学习一组可微分的分配矩阵S∈n×m，将n节点映射到m节点形成不同粒度的特征层输出，从而支撑池化和上采样层的设计。具体通过两次卷积运算实现，即：和其中,Convembed为了生成新的节点特征，Convpool为了获得到节点之间的分配矩阵，并通过Softmax函数归一化。基于此，(l+1)层图的邻接矩阵和节点特征矩阵分别更新为

(2)

(3)

在上述过程中，图节点的数量和特征维度得到了调整。当m小于n时，节点数量减少，理解为对节点进行了聚类以得到粗化输出，即图的池化运算，以获取不同粒度的特征。当m大于n时，节点数量增加，即图的上采样运算，以恢复图的尺寸。

1.2.3 损失函数

该模型通过非监督方式进行训练，训练目标为最小化输入和输出之间的差异。考虑到池化运算中分配矩阵优化的困难性，文献[26]在损失函数中加入两组约束，分别是每层邻接矩阵差异最小化以及分配矩阵逐行的熵最小化。其中，前者保障邻接矩阵中边的稳定性，后者保障每个节点的分配概率接近一位有效向量(one-hot vector)，以清晰地表达其与下一层输出之间的关系。最终损失函数定义为

(4)

2 形状自适应的建筑物化简算法选择模型

本文通过机器学习模型分析上述获取的建筑物编码，并从多个候选化简算法中选择最适合处理该建筑物的算法，该过程包括两部分：候选建筑物化简算法和利用机器学习的算法选择模型。

2.1 建筑物化简候选算法集

如前所述，目前已经提出了多种建筑物化简算法。理论上，越多的化简算法作为候选，越有利于为每个建筑物提供高质量的化简方案，但也会使得构建的选择模型越复杂。综合考虑，本文选择矩形拟合法[21]、模板匹配法[15]、邻近四点法[8]、迭代法[13]作为每个建筑物实施化简的候选算法。这4种算法的基本原理、适用范围及局限性总结见表1。一方面，这4种算法的设计原理互不相同，面对不同形状建筑物时优缺点互补性强；另一方面，它们都是基于矢量的化简方法并且采用简单参数实现，便于生成化简程度相近的输出结果。

表1 4种候选化简算法比较Tab.1 Comparison of four candidate building simplification algorithms

2.2 建筑物化简算法选择模型

本文目标在于建立形状自适应的化简算法选择模型，即依据建筑物的形状编码从候选算法集中选择最佳算法进行化简。该过程是一个多分类问题，输入为32维的建筑物形状编码，输出为4维向量，分别代表使用4种化简算法的适宜性。该问题可以利用监督式机器学习分类方法构建得到算法选择模型。构建模型时，首先利用一部分带标注的建筑物编码样本，即标注每一个建筑物最适合的化简算法，对分类器进行训练，获取分类知识；随后，逐个输入建筑物的形状编码，模型以概率形式表达预测其最适合的化简算法。该过程如图4所示。

图4 基于监督学习的建筑物化简算法选择模型Fig.4 Selection model of building simplification algorithms using a supervised learning

很多机器学习分类模型可以完成上述任务，例如人工神经网络(backpropagation neural network,BPNN)、支持向量机(support vector machine，SVM)、随机森林(random forest,RF)等。在利用这些学习模型构建用于建筑物化简算法选择的分类器时，不需要建立特殊的数据组织方式或运算技巧，采用通用模型即可。因此，基于不同学习模型构建分类器的原理和过程不再赘述。

3 试验分析

本文使用1∶1万比例尺建筑物数据进行试验分析。其中，训练建筑物数据选自住宅、商业、工业等不同城市功能区，总数为1000个。对建筑物预处理后，应用四种算法化简，并由人工标注出最佳算法。化简目标比例尺为1∶2.5万，参考制图规范将化简阈值定义为最短边长度不小于6 m；对于矩形拟合法和模板匹配法，如果其最短边长没有达到该阈值，则进行适当放大处理。在模板匹配法中，使用了人工建立的包含61个模板的建筑物库。试验使用两组数据集进行测试，数据集Ⅰ包含219个来自住宅区的建筑物，尺寸相对较小、形状比较规范；数据集Ⅱ包含222个来自商业区的建筑物，尺寸相对较大、形状较为复杂。测试集的处理过程和参数与训练集一致。

3.1 化简质量评价指标

为了定量评价化简结果，本文采用如下指标度量化简前后建筑物多边形的位置、面积方向和形状变化以及化简后正交特征。

(1) 位置变化指标。设原始建筑物边界节点p1,p2,…,pn,n表示节点数量。节点pi的位置变化定义为该点到化简后多边形边界的最近距离d(pi)。化简前后整体位置变化通过所有节点位移平均值来描述，计算为

(5)

(2) 方向变化指标。方向变化指标通过最小外接矩形长边的方向变化值来度量，计算为

(6)

式中，Ob和Oa分别表示化简前后最小外接矩形长边与X轴方向的夹角。

(3) 面积变化指标。面积变化通过化简前后建筑物多边形的面积差值来度量，计算为

(7)

式中，Ab和Aa分别表示化简前后的面积。

(4) 形状变化指标。建筑物形状通过边界上的点沿参考方向(如x轴)切角变化情况来描述，即转交函数[27]，表示方法为一维分段函数。形状变化则由化简前后建筑物多边形对应的转角函数组成的空间距离来表示，即

(8)

式中，fb(s)和fa(s)分别表示化简前后建筑物多边形的转角函数；θ代表建筑物多边形的旋转角度；t代表自起点沿多边形行进的弧长。如图5所示，形状变化即两组转交曲线所围成的区域范围大小。

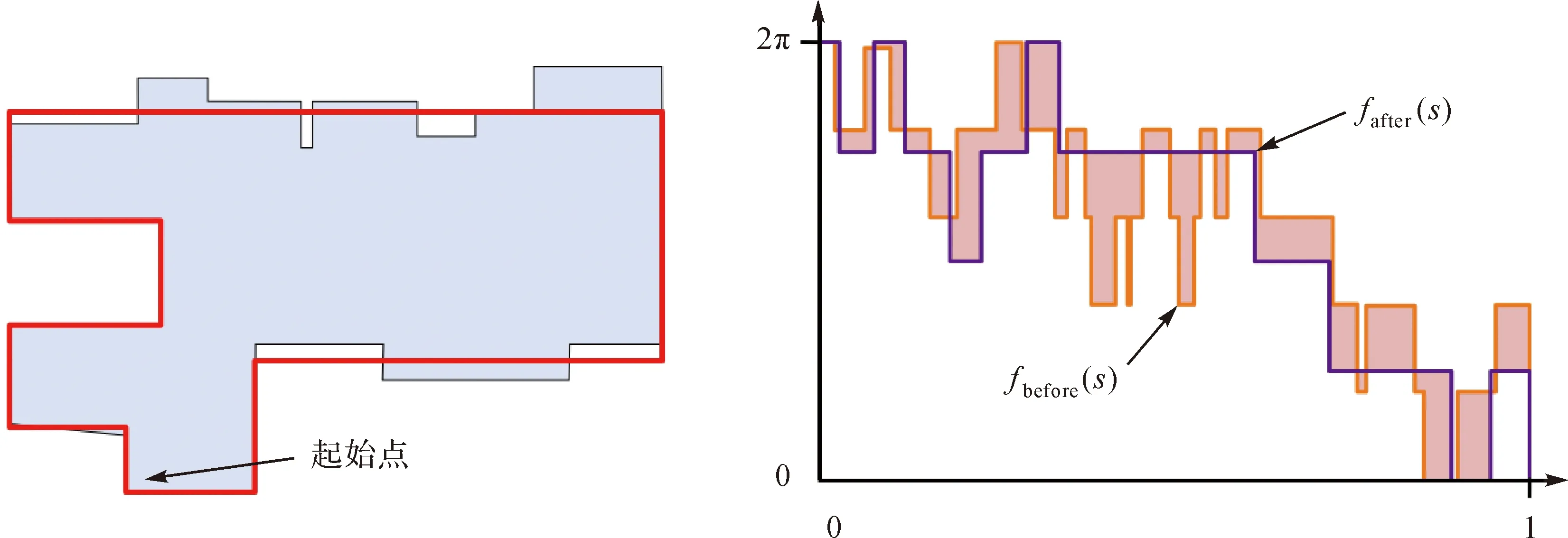
图5 化简前后建筑物形状变化度量Fig.5 Shape change measurement of the building polygons before and after simplification using turning function

(9)

式中，αi表示化简后建筑物多边形相邻两边形成的夹角；n为多边形节点数。

3.2 建筑物形状编码结果与分析

本文首先利用上述构建的图卷积自编码学习模型对试验数据集中的全部建筑物进行训练，获取形状编码库。模型采用Adam算法优化，学习率为0.2，迭代次数为200。为了清晰地展现编码效果，利用t-SNE算法[28]将全部建筑物编码降维至二维并在平面空间可视化，结果如图6所示。

可以看到，在编码空间中距离较近的建筑物，其形状在视觉上也较为接近；而距离较远的建筑物，其形状在视觉上也差异较大。例如，在图6上方区域的建筑物形状接近矩形状和圆状，较为相似；而右下方区域则集中分布为L型、U型、E型、锯齿扁平状建筑物。该结果表明本文提出的图卷积编码模型对形状特征具备较好的表征能力。后续即利用监督学习模型在该特征空间中进行非线性化分类，从而区分出不同形状特征所对应的最佳化简算法。

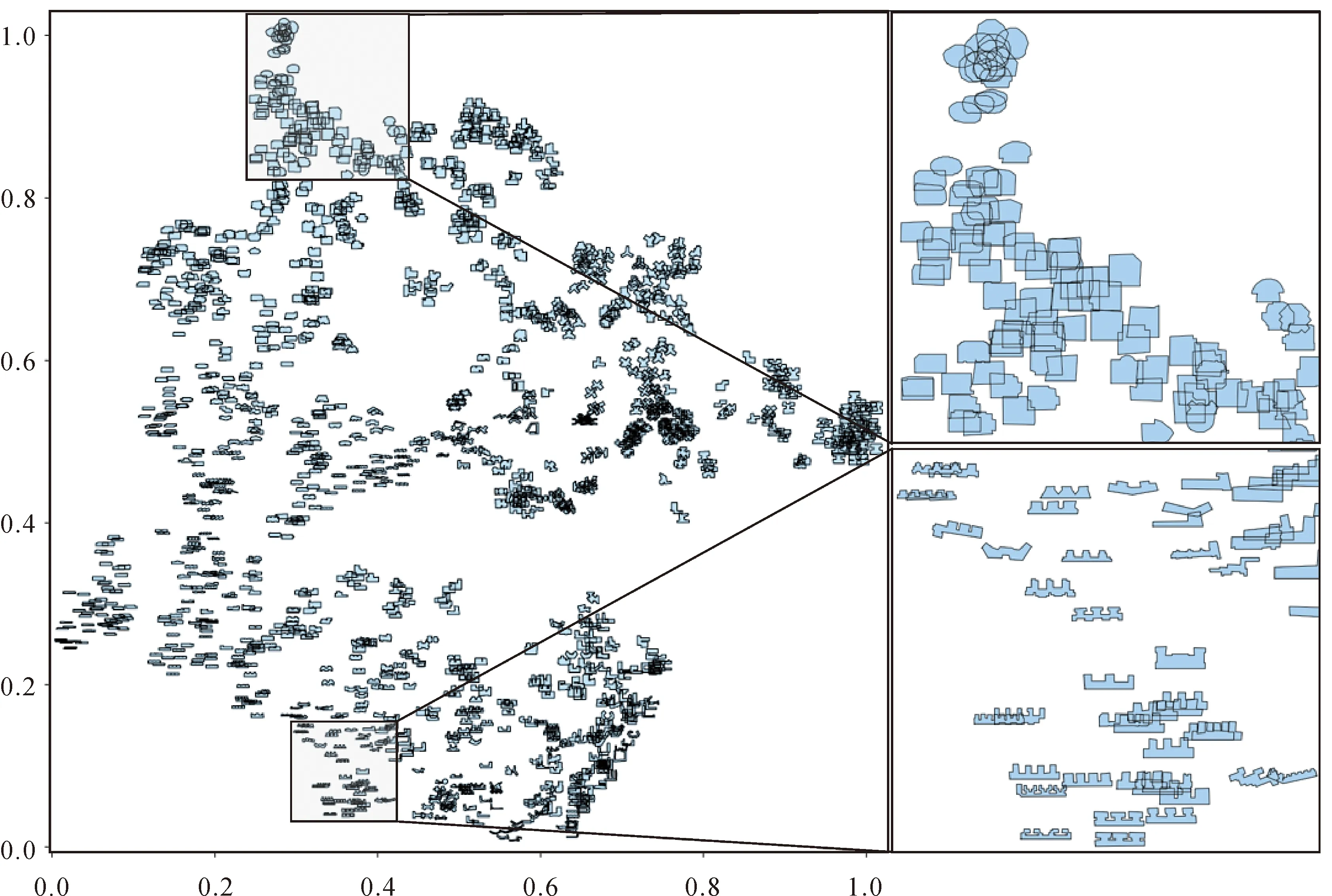
图6 形状特征表达的可视化Fig.6 Visualization of the shape representation using the proposed graph-based autoencoding architecture

3.3 分类结果与分析

本文使用BPNN、SVM、RF这3种机器学习方法构建化简算法选择模型。本文分别设置BPNN模型中隐含层神经元数量为4、8、12、20和30进行对比试验，训练次数都为100 000；RF模型中决策树数量设置为30、50和100进行对比；SVM模型则分别采用线性和高斯核函数以实现线性和非线性优化拟合的对比。表2为不同参数下3个模型在两组测试数据集上的分类准确率。

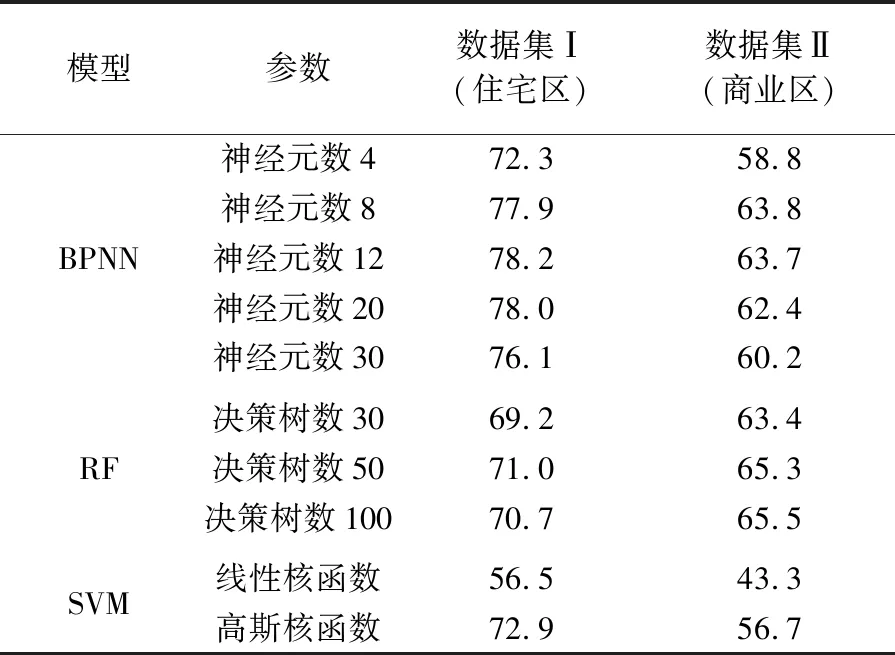
表2 不同机器学习方法支持下化简算法选择模型的分类精度Tab.2 Classification accuracies of the simplification algorithm selection using different machine learning models (%)

可以看到，BPNN模型在较少神经元时分类精度较低，随着神经元数据增加，精度有所提升且表现稳定；但神经元达到一定数量，精度略微下降，这可能与模型复杂程度以及训练数据量相关。综合两个数据集的结果，BPNN模型中神经元数量为12时表现较佳。RF模型在不同的决策树数量参数下分类精度变化并不大。但是对于SVM模型，采用线性核的分类精度远低于高斯非线性核。

对比3种模型，BPNN模型在数据集Ⅰ的最佳精度达到78.2%，相比SVM和RF模型有一定的优势，但是在数据集Ⅱ中的精度为63.7%，略逊于RF模型。RF模型在数据集Ⅰ精度低于BPNN及非线性SVM模型，但在数据集Ⅱ上精度达65%，优于其他模型。对比两组数据集，3种模型都是在数据集Ⅰ中的表现优于数据集Ⅱ。分析可能的原因是住宅区中建筑物面积一般较小、形态特征比较简单显著；并且局部范围内的建筑物往往呈现相似的形状、具备相近的尺寸，适合采用相同的化简算法进行处理。因此，在编码器将相似形状表征后，分类器能具备较好的区分能力。相比较之下，商业区中的建筑物形状和尺寸差别较大，形状较为复杂、相似性也不强，导致模型进行不同化简算法选择时难度系数提升。特别是针对都适合处理较为复杂形状的邻近四点法和迭代法，模型很难获得与人工一致性较高的判断知识。

3.4 建筑物化简结果与分析

上述结果表明BPNN模型总体上表现较好。因此，本文进一步以包含12个神经元的BPNN模型产生的分类结果为基础，分析测试数据集的化简结果，部分建筑物化简前后状态对比如图7所示。表3给出了测试集中所有建筑物评价指标的平均值，同时给出了分别使用4个单一算法化简的结果指标。

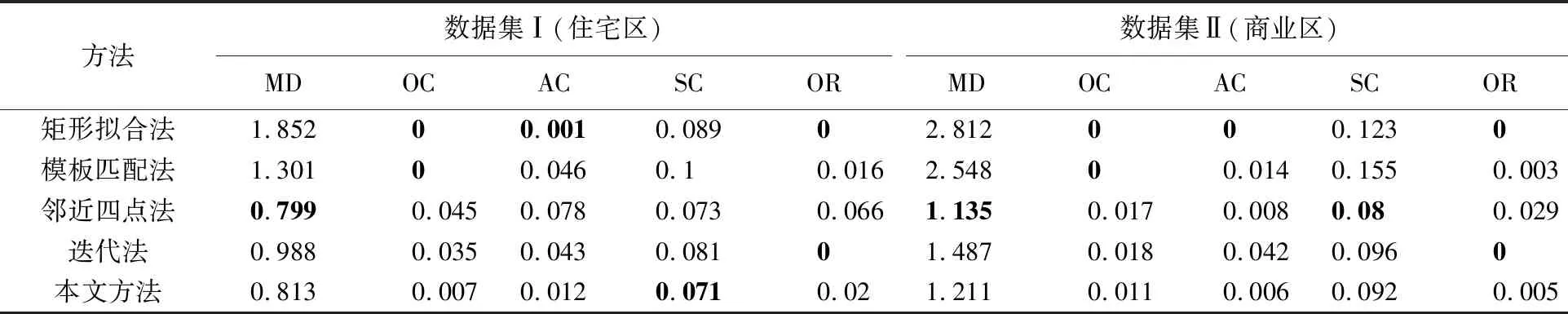
表3 利用不同方法化简的结果评价指标Tab.3 Evaluation of the simplified results produced by different methods

可以看到，单一算法在某些指标上具有一定的优势。例如矩形拟合法在面积、方向保持以及正交性特征指标上最优，原因在于其化简时会缩放最小外接矩形使其面积和方向保持与原始形状一致，这是强约束，同时也能保证化简后多边形4个角都是直角。邻近四点法在位置保持指标上表现良好，原因在于其化简动作是通过移动或删除局部凹凸结构实现的，只会处理一部分结构点，因此其平均位置移动最小。但是单一算法很难兼顾全部的指标，例如矩形拟合法和模板匹配法的位置指标表现欠佳，表明其化简后存在较大的位置偏移；迭代法和邻近四点法在方向和面积保持方面欠优，表明这两种局部处理的策略，可能会造成整体形状特征出现失衡。

总体而言，本文方法在各指标上都表现出一定优势和协调性，特别是在数据集Ⅰ中形状保持方面表现最佳。这表明，本文方法不会产生效果极差的结果。虽然在某些指标上略逊色于单一算法方法，但这也是合理的。因为并不是某项指标保持得好，该化简效果就合理。例如在矩形拟合法中，虽然方向、面积、垂直性都保持良好，但并不意味着化简结果好，对一些复杂形状可能会存在非常严重的形状变化。从图7化简结果中也可以验证这一点，每一种算法都或多或少存在不合理的化简情况，而本文方法总体上保持比较均衡，效果良好。

前文中指出由于数据集Ⅱ中的建筑物形态较为复杂、尺寸差异较大，算法选择时分类精度较低，因此也进一步影响了后续化简过程。例如表3中，在数据集Ⅱ中化简指标整体较数据集Ⅰ略差。但差距不是很明显，同时从图7(b)中也可以看到数据集Ⅱ中很多建筑物也能取得较好的化简效果。分析可能的原因是一个建筑物可能存在多种化简算法，其效果比较接近且都能满足化简需求。因此，在部分情况下，就算自动选择的算法与人工选择的算法不一致，但是其化简结果也是可以接受的。

4 结 论

针对建筑物化简这一长期面临挑战的问题，本文提出了基于形状特征认知的自适应化简方法。该方法首先通过图卷积深度学习建立建筑物形状的特征表达，然后利用机器学习技术建立形状表达与不同化简算法之间的选择模型。试验结果及相关分析表明：①基于图的自编码器能有效地表征建筑物形状特征，相似的建筑物形状在编码空间中，距离也更为接近；②基于机器学习的算法选择模型对于住宅区建筑物表现较好，精度达到78.2%，应用于形态和尺寸变化多样的商业区建筑物表现略差；③本文方法的化简结果在位置、方向、面积和形状变化等指标上，总体上优于运用单一算法获得的化简结果。

下一步工作包括：①本文以形状特征作为建筑物化简算法选择的判断依据，后续进一步考虑尺寸、区域地理环境特征(如城中村)等其他指标；②加入其他建筑物化简算法，进一步丰富候选化简算法集。此外，本文方法中形状编码表达和化简算法选择是相互独立的，后续研究可考虑构建模型集成这两个过程，即将化简算法的选择作为图卷积模型的训练目标。