动平台分布式相参雷达自校准性能分析

卢佳欣 孙静宜 刘飞峰 刘泉华 缪颖杰

（北京理工大学信息与电子学院雷达技术研究所，北京 100081）

1 引言

分布式相参雷达最近逐渐获得关注，其最早由林肯实验室提出［1］，指若干机动式单元雷达通过接收相参和发射相参等效形成大孔径相控阵雷达。针对分布式相参雷达提高信噪比的目标，文献［2-4］提出了新的思路，通过直接传递时钟信号的方式实现多个雷达节点的时频同步，通过开环发射相参以直接在目标处实现相参积累，但这些方案需要对单元雷达节点的位置精确已知。

同时，文献［5-6］提出了分布式相参雷达具有高精度测角的潜力，该模型作为统计MIMO 雷达的相参模式在文献［7-8］中也被提出。但动平台雷达节点的位置偏差和速度偏差会对目标测角和测速造成很大影响。

针对分布式雷达节点位置偏差和速度偏差，可采用校准算法对偏差量进行估计。根据文献［9］可知，校准算法分为有源校准和自校准，两者的区别在于校准点的位置是否精确已知。对于动平台分布式相参雷达系统，其在工作场景中较难在观测区域安置位置精确已知的校准点，故而自校准算法在分布式相参雷达中的应用是必要的。对于自校准算法，最关心的问题是多少个校准点可以实现误差参数估计的可分辨。参数可分辨意味着具有更加精确参数估计结果的潜力，这对校准问题是一个极具吸引力的性质。［10-11］均采用混合克拉美罗界（hybrid Cramer-Rao Bound，HCRB）对参数估计的可分辨性进行分析。而HCRB紧致性是其应用的前提，故而本文首先对HCRB紧致性进行分析，之后应用HCRB推导了目标角度估计精度曲线趋于水平时的精度大小的解析式。

后续内容安排如下：文章第2节对动平台分布式相参雷达进行建模，阐明待估计参数；第3节对混合克拉美罗界的紧致性和测角精度的显性表达式进行推导；第4节进行了仿真验证；第5节总结全文。

2 动平台分布式相参雷达建模

本小节主要是对动平台分布式相参雷达的系统拓扑、回波信号以及误差进行建模。动平台分布式相参雷达拓扑如图1所示。

图1 中，在t=0 时刻，以首个雷达节点为坐标系原点，首个雷达节点和第二雷达节点的连线方向为x轴。x轴附近的实心点和实线箭头分别代表雷达节点的真实位置和真实速度；空心点和虚线箭头分别代表雷达节点的理论位置和理论速度。图中的分别代表第q个目标的角度、距离、切向速度和径向速度。

设分布式雷达系统K发L收，并设目标个数为Q。则分别为第k个雷达节点发射，第q个目标反射，第l个雷达节点接收的回波时延和多普勒。则第m个慢时间，第l个接收机的回波数据如下：

设第k个发射机和第l个接收机的真实位置分别为。设第k个发射机和第l个接收机的真实速度分别为和。设第q个目标的位置和速度分别为

其中c代表光速，‖·‖2代表l2范数。

其中λ代表载频波长。

设

此时中间待估计量所构成的向量可被定义如下：

其中

假设动平台分布式相参雷达收发共址，则最终待估计参量所构成的向量可被定义如下：

其中

设y=[y11[1]，y11[2]，…，y11[N]，…，yLM[N]]T∈CLMN×1。

3 HCRB紧致性研究及误差对目标参数估计精度恶化性能评估

克拉美罗界的使用通常是通过紧致性来证明其合理性，即若下界是紧致的，则此下界是有效的；反之，则下界无效。紧致性表明在性能界曲线进入渐近区时，即当信号拥有“足够大”的信噪比（SNR）或长时间积累时，最大似然估计器的估计精度会贴合此性能界曲线的现象。因而只有当所推导的性能界是紧致的，该性能界才可以准确表征估计器的性能。

本节是基于第2 节的建模进行的HCRB 相关性质推导，主要推导了HCRB 的紧致性及在不可分辨场景下目标角度估计的最佳测角精度的显性表达式。

3.1 HCRB的紧致性

由于待估计参数中目标参数是非随机参数，而定位误差和速度误差是随机参数，因此根据文献［12］，可以利用HCRB 工具对待估计参数的估计精度进行建模。

HCRB的公式如下：

其中

上式中，Jγ是中间待估计参量γ的信息矩阵；P为链式法则矩阵；Jr是雷达节点位置偏差的方差和速度偏差的方差构成的对角矩阵。

由文献［13］可知，当PTJγP中不含有最终待估计参量α中的随机参量时，

若PTJγP中不含有最终待估计参量α中的随机参量，则

上式中，α0代表雷达节点偏差量均为0 的场景，即

由于式（13）仅在雷达节点偏差量较小时才能近似成立，故而HCRB 仅在雷达节点偏差量较小时才是紧致的。

3.2 目标参数估计不可分辨情况建模及解析式推导

不可分辨指待估计参量的估计精度曲线随着信噪比的提高而趋于水平，这是由于误差的存在导致目标参数和雷达误差参数无法更加精确的估计。本小节推导了目标角度估计精度曲线趋于水平时的精度大小的解析式，旨在可以直观的分析雷达系统参数及拓扑参数对于目标参数估计精度的影响，有利于后续雷达系统硬件参数的选择和设计。

设链式法则中的矩阵

其中，R是中间待估计参量关于目标参量的微分；S是中间待估计参量关于雷达系统偏差的微分。

那么

成立。其中Jγ=，k=SNR，则信息矩阵J如下所示

利用求逆公式可得目标参数估计的性能界表达式如下

如果没有偏差，则上式中S矩阵缺失，此时

当k→∞时，

其中V-是V矩阵的伪逆。若采用MATLAB 代码进行仿真，注意对函数容差进行人工设定；I代表单位矩阵。

4 仿真分析

为了验证第3 节所推导的显性表达式，本节进行了数值仿真，仿真参数表格如下表1所示。

图2 为利用表1 的边界条件仿真目标角度位于雷达节点-45°时的目标参数估计精度曲线图。图（a）是三节点雷达系统，单目标的系统拓扑图。图（b）、（c）、（d）分别是仿真得到的目标角度、切向速度和径向速度估计精度曲线。其中黑色圆圈曲线为利用公式（24）求得的解析解曲线，黑色方框曲线为利用HCRB公式求得的目标角度估计曲线，观察得到在高信噪比情况下，圆圈曲线和方框曲线重合，印证了不可分辨情况下雷达节点系统误差影响下的目标参数估计精度的解析解公式推导的正确性。

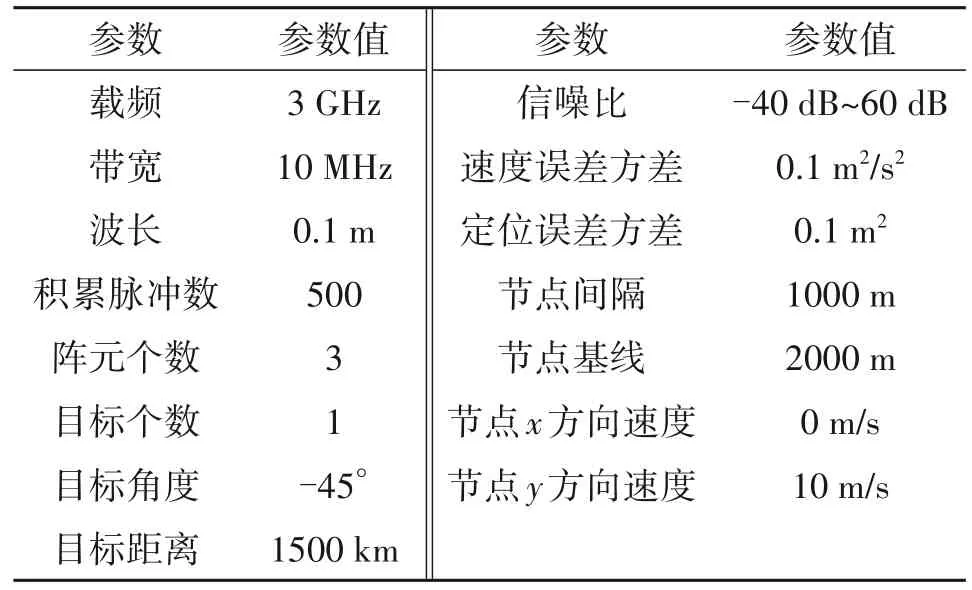
表1 仿真参数Tab.1 Simulation parameters

5 结论

本文首先对系统误差下的混合克拉美罗界进行建模，并且分析了混合克拉美罗界紧致性的条件，最后对测角精度的显性表达式进行计算并通过数值仿真进行验证。分布式相参雷达系统作为原理样机最早在林肯实验室已经完成了测试，但是其在实际应用中还面临着诸如杂波、同步等问题，这些问题的解决也是我们后续的工作方向。