基于机动检测的参数自适应跟踪算法

张 娜 王 锐 蔡 炯

（北京理工大学信息与电子学院，北京 100081）

1 引言

目标跟踪在民事和军事领域有着广泛的应用，在跟踪过程中，量测噪声及目标机动等会导致跟踪精度下降、跟踪发散等问题。当前机动跟踪算法研究主要是围绕目标机动发生时间的不确定性展开，可分为基于决策的单模型算法与多模型算法，多模型算法采用多个并行模型来描述目标的运动模式，通过对各子滤波器进行加权融合获得最终的状态估计，其跟踪性能依赖于选取的模型集，设计过程较为复杂且计算量较大，研究［1］表明，若辅以良好的机动检测方法，单模型算法可获得与多模算法相近的性能。

单模型算法使用单一的模型进行滤波，常用的模型有匀速模型（Constant Velocity，CV）模型、匀加速模型（Constant Acceleration，CA）模型、匀转弯（Constant Turn，CT）模型、Singer 模型以及当前统计模型（Current Statistics，CS）［2］等等，其中CS 模型具有更全面描述目标机动特性的能力，获得广泛的应用。但基于单模型的跟踪算法往往难以很好地平衡跟踪精度与对机动的快速响应能力，特别是当目标机动能力越来越强，目标运动模型的结构、参数等发生变化，而传统单模型算法无法及时准确地对模型、滤波参数做出调整，导致跟踪效果不理想，为此，研究人员提出很多自适应滤波算法。

首先是模型参数的自适应调整，CS模型性能的发挥依赖两个参数：机动频率和加速度极值，不同的运动状态对二者的需求是不同的，因而往往很难提前给出一个合适的参数值，若运动形式发生变化，固定的参数值将导致精度降低，甚至造成滤波发散，因此有必要对CS 模型的参数进行自适应调整，使之与目标运动状态更加匹配。基于此，文献［3］基于新息构建指数函数对机动频率进行自适应调整，文献［4］使用新息主导的隶属函数自适应调整机动频率，文献［5］采用反正切函数的变体来自适应调整加速度极值，文献［6］利用新息特性，调整加速度极值，并利用连续三个时刻的加速度信息，推导出一种自适应机动频率表达式。而通过分析，加速度极值主要用于计算过程噪声，可直接对过程噪声进行自适应调整，Sage-Husa［7］算法可在线估计噪声统计特性，但可能会出现矩阵非正定和滤波发散等现象，文献［8］利用新息序列的实时信息计算过程噪声，文献［9］应用新息和残差序列推导的线性矩阵方程实时求解噪声协方差。

模型参数自适应调整算法对机动时刻的跟踪性能的改善有限，在目标机动时几乎不可能进行精确的运动建模［10］，需使用自适应滤波算法来应对目标的突然机动。强跟踪滤波［11］（Strong Tracking Filtering，STF）可保持算法对机动目标的跟踪能力，通过强迫残差序列协方差值与理论值相等来确定渐消因子，并在渐消因子大于1 时调整预测状态协方差矩阵，使得算法具有较强的应对突发机动的能力。但渐消因子的引入条件过于宽松［12］，导致在不需要引入渐消因子的时候引入渐消因子，影响稳态时的跟踪精度。

针对当前统计卡尔曼滤波算法难以兼顾稳态跟踪精度与机动响应速度等问题，本文基于新息的高斯统计特性构造判决函数并进行机动检测，根据三种不同的检测结果，采取不同的调整策略，以提升算法的跟踪性能。主要贡献如下：

一是自适应CS模型，利用上一时刻与当前时刻预测协方差矩阵的加速度分量完成机动频率和加速度方差的自适应调整，提高算法对弱机动目标的跟踪性能。

二是自适应滤波算法，依据检测结果，在适当的时机引入渐消因子，通过渐消因子调整预测协方差矩阵，提高算法对突发机动响应能力。

通过上述两方面调整，基于机动检测的自适应算法在提高对弱机动跟踪性能的同时，增强了对突发机动的跟踪能力。

2 算法原理

2.1 CS模型分析

CS 模型假设目标下一时刻的加速在当前时刻加速度附近变化，其性能依赖于机动频率α和加速度极值a±max两个参数，当预先设定的参数与实际情况不符时，跟踪精度会降低。分析各参数对滤波性能的影响有助于辨识目标运动模式的变化，并能够及时调整模型结构、参数等，进而提高跟踪精度。在CS模型中，机动频率和加速度极值主要是对状态转移矩阵F、过程噪声方差Q产生影响。

状态转移矩阵表示为：

对式（1）取极值分析，随着α逐渐减小，CS 模型逐渐逼近常加速度CA模型，反之，随α逐渐增大，CS模型逐渐逼近常速CV 模型，当0＜αT＜∞时，CS模型对应于某一种介于常速和常加速之间的运动。

过程噪声方差表示为：Qk=，其中qcs、是α的函数，具体形式可参考文献［2］为机动加速度修正瑞利分布的方差，满足：

式中a±max表示加速度极值，aˉ为加速度均值，在卡尔曼滤波体系下，将前一时刻的加速度估计值作为加速度均值，即。由式（2），若加速度取值较大，当目标处于弱机动状态时，加速度远小于最大加速度，则过程噪声会处于一个较大的量级，而过大的Q会导致模型失去预测作用，因而并不适合非机动和弱机动目标的跟踪；若为兼顾对弱机动的跟踪精度设置较小的加速度极值，算法对机动适应能力就会降低。

通过上述分析，机动频率和加速度极值是影响跟踪精度的两个关键因素。对于机动频率，文献［13］认为机动频率α在过程噪声方差和状态转移矩阵中对增益的影响是相反的，因而不能单纯的认为机动频率与机动强度成正相关。对于加速度极值，由式（2），加速度极值主要通过加速度方差对滤波产生影响，因而可将加速度极值的调整转换为对加速度方差的估计。

2.2 基于机动检测的参数自适应跟踪算法

本文基于新息的高斯统计特性构造判决函数并进行机动检测，根据检测结果采取不同的参数调整策略。

2.2.1 机动检测算法

机动检测本质上是一种判别机制，目标机动带来最直观的变化是测量新息的变化，利用新息变化制定机动检测的决策逻辑，成为主要的发展方向［14］。传统χ2检测算法以新息为输入构建统计量，通过比较统计量与单一固定门限之间的大小来判断是否发生机动，但单一门限会导致虚警与漏检之间的矛盾，且χ2检测算法对大幅值突变机动具有较好的检测效果，对于小幅值的故障检测效果比较差。本文依据新息的高斯分布性质，构造双阈值门限来进行机动检测：

式中，vk、Sk分别表示量测新息及其协方差，当检验统计量小于时，表示无机动发生，调整CS 模型参数，使模型与目标运动模式更加匹配，提高稳态跟踪的精度；当统计量处于时，认为当前量测数据质量较差或目标进行小幅机动，无法给出当前目标有无机动的肯定判决，保持模型参数不变；当判定当前时刻发生机动，借鉴强跟踪滤波思想，引入次优渐消因子调整状态预测方差，调整CS模型参数，渐消因子以及修正后的状态方差计算公式如下：

式中，R表示量测噪声方差，Q表示过程噪声方差矩阵，H表示量测矩阵，F表示状态转移矩阵，Pk-1表示卡尔曼滤波过程中的前一时刻的状态方差矩阵。

2.2.2 CS模型参数自适应

状态预测协方差矩阵Pk可用来衡量预测的不确定性，其加速度分量可用于衡量加速度预测的不确定性，因此可以根据设计机动频率、加速度方差自适应调整方案，改善CS模型参数不能自适应调整以及对弱机动目标跟踪精度不高的问题。

机动频率自适应调整。首先，固定采样间隔T与加速度方差，分析卡尔曼滤波框架下机动频率对稳态增益的影响，并在上述基础上，限定α值在(0，0.1/T]范围内，认为在上述区间内，稳态增益是关于α的单调函数，机动频率与机动强度成正相关，因此利用下式对机动频率进行自适应调整：

加速度方差自适应调整。文献［15］利用估计方差阵Pk中加速度分量来代替方差，而无需加速度极值的先验信息：

过程噪声方差：

综上可知，改进的CS模型将机动频率、加速度方差的计算与状态协方差矩阵的相关元素相联系，从而可与滤波算法结合，实现对目标的自适应跟踪。

基于机动检测的参数自适应跟踪算法流程图如图1所示。

算法实现过程如表1所示。

表1 基于机动检测的自适应跟踪算法具体实现Tab.1 Implementation of adaptive tracking algorithm based on maneuver detection

3 仿真与实测数据验证

3.1 机动频率对稳态增益的影响

首先，分析卡尔曼滤波框架下机动频率对稳态增益的影响，分别在采样周期T=1 和T=10 假设下，仿真得到稳态时的位置增益K(1，1)随机动频率变化曲线如图2。

从图中可以看出，稳态增益K(1，1)并不是关于α的单调函数，但在α的部分区间内，可视为单调函数。假定αT∈(0，0，1)，绘制不同采样间隔下的K(1，1)变化曲线。

可以看到，当α∈(0，0.1/T]时，稳态增益是关于α的单调函数，机动频率与机动强度成正相关，即：目标机动增强时需增大机动频率，机动减弱时应减小机动频率。

3.2 仿真验证

为验证算法的有效性，采用100 次Monte Carlo仿真，采用均方根误差（Root Mean Square Error，RMSE）来评价算法的性能，RMSE 越小，表示滤波估计值与真实值越接近，跟踪精度越高。本文在以下三种场景中对所提算法进行仿真分析，并与传统基于CS 模型的卡尔曼滤波算法进行比较。假设目标在一维平面作机动运动，过程噪声与量测噪声均为高斯白噪声序列。

场景1：匀速运动，在该场景下对传统算法与所提算法进行比较。

图4 分别为估计值的位置、速度和加速度误差根均方差对比。

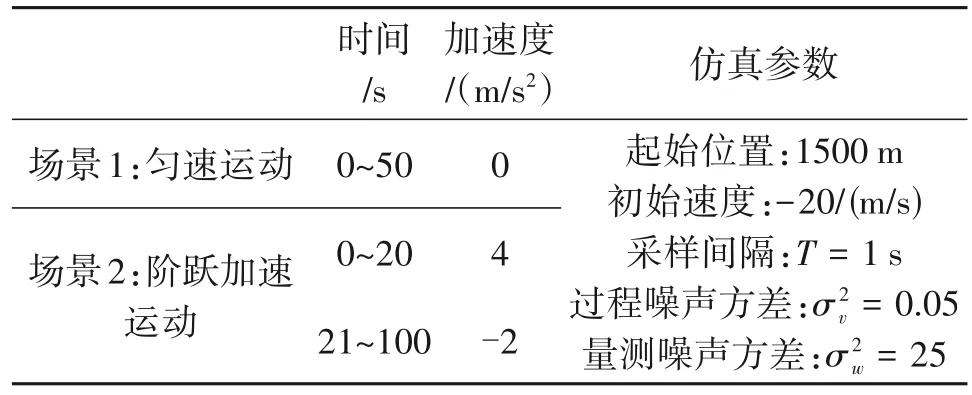
表2 一维平面中目标运动场景及仿真参数Tab.2 Target motion scene and simulation parameters in 1D plane

图4分别展示了两种算法的位置、速度、加速度均方根误差，可以看到，对于匀速运动这类弱机动运动，所提自适应算法的RMSE 要低于传统的基于CS模型的卡尔曼滤波算法，即自适应算法精度更高，尤其是速度和加速度，估计精度改善更为明显。

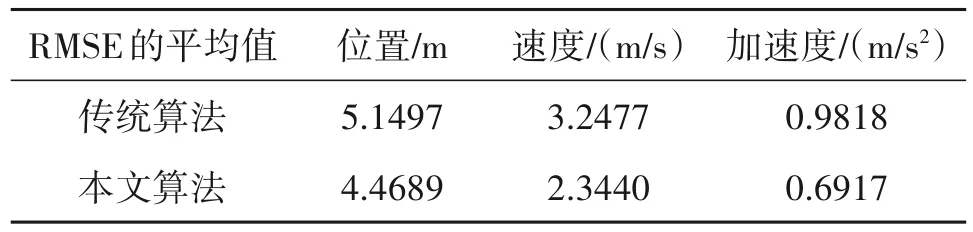
表3 匀速场景中均方根误差的平均值比较Tab.3 Comparison of the average value of the RMSE in the uniform speed scene

场景2：阶跃加速运动，在该场景中主要考察算法对机动的响应能力。

表4 机动延迟时间、虚警率、漏检次数Tab.4 Maneuver delay time，false alarm rate and missed detection rate

根据图5，对比两种算法的渐消因子引入时机，可注意到强跟踪滤波算法在未发生机动时刻也引入渐消因子，而本文通过基于新息分布的机动检测算法，可有效降低渐消因子引入次数，进而提高滤波算法在稳态时刻的跟踪性能，以下为传统算法与本文算法结果对比。

从图6 的均方根误差曲线可看出，在加速度发生突变的时刻，即目标发生机动时，RMSE 曲线会出现峰值，这是因为跟踪算法需要时间进行参数调整或估计，峰值持续时间越短，意味着跟踪算法对机动的响应速度越快，算法适应能力越强，可以很明显看到，对于位置信息的跟踪估计，自适应算法的位置均方根误差显著降低，但速度与加速度在机动时刻的估计精度略有下降。

场景3：在极坐标中比较算法性能，目标初始位置(2×103，104)m，匀速运动速度(290，290)m/s。

量测噪声方差矩阵：R=diag([200，0.02])，分别为距离、角度量测误差的方差，采样间隔T=2 s，跟踪结果如图7所示。

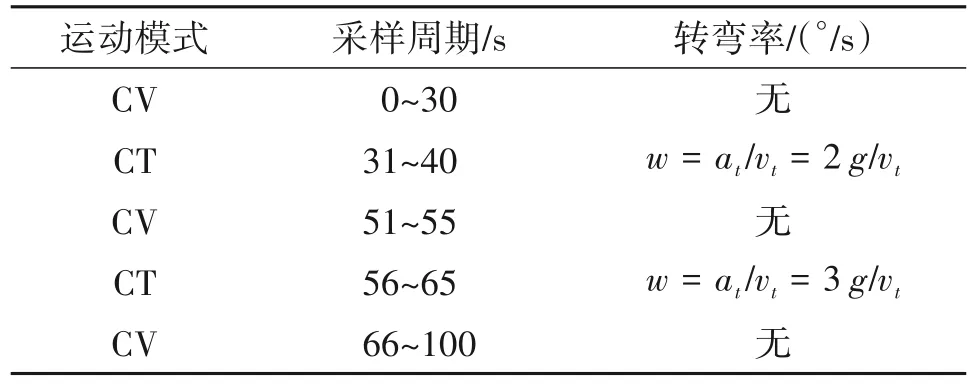
表5 二维平面中目标运动场景及仿真参数Tab.5 Target motion scene and simulation parameters in 2D plane

可以看出，对于31～40 s、56～65 s 之间的两段转弯运动，传统算法在目标发生机动时，误差曲线会出现较大的尖峰值，而本文算法虽然也存在峰值，但相较传统算法峰值显著下降，滤波稳定性更强。

为进一步分析算法性能，我们以场景3 为实验条件，分析两种算法的时间复杂度，表6 统计了100 次蒙特卡洛实验中两种滤波算法的运行时间。传统KF-CS 滤波算法涉及加速度方差的计算，自适应算法无需计算加速度方差，但引入量测各维度的机动检测，以及机动频率、加速度方差自适应调整因子的计算以及在机动发生后渐消因子的计算，增加了一定的计算量，但算法效率也符合预期。

表6 时间复杂度比较Tab.6 Comparison of time complexity

综合上述仿真结果，本文算法在位置、速度、加速度跟踪精度较传统算法有所提高，且时间复杂度只是略有增加，实时性较好，因此算法满足机动目标跟踪对跟踪精度和实时性的要求。

3.3 实测数据验证

为进一步验证算法的实际跟踪性能，我们以折返飞行的小型无人机为目标，利用雷达进行回波采集实验数据进行算法验证。雷达采集场景中，主要为平坦的田地，强地面杂波少，因此，经过恒虚警处理后剩余杂波点较少，利用简单的最近邻关联算法即可实现点迹与航迹的关联，由于真实航迹是未知的，因而无法给出与其他算法的RMSE误差对比，仅给出了航迹的估计结果。图8为斜距、方位角、俯仰角跟踪结果。

图8展示了雷达采集到的量测点集分别基于传统算法和本文自适应算法对目标量测数据的估计航迹。从整体来看，算法可从量测数据中提取出目标的航迹信息，对实测数据的跟踪结果良好，对于短暂量测缺失，可通过预测值进行代替，提高航迹的连续性，但对于连续量测丢失的情况，会出现航迹断裂的现象。从局部来看，传统算法会出现较为剧烈的震荡起伏，特别是角度跟踪结果，本文算法滤波性能更优。

4 结论

针对传统CS 卡尔曼滤波算法无法兼顾稳态精度与机动响应速度的问题，本文在机动检测框架下，进行参数自适应调整。目标未发生机动，基于加速度预测协方差信息调整CS模型参数，目标发生机动，引入渐消因子调整预测协方差矩阵，并根据修正后的预测协方差矩阵调整CS模型参数，当难以界定目标有无机动时，不做任何调整，保持当前参数。算法将模型参数的调整与滤波过程相结合，提高了对弱机动运动的跟踪精度，同时在恰当的时机引入渐消因子，通过调整预测协方差矩阵，提高算法对突变机动的响应能力。