端到端的梯度提升网络分类过程可视化

葛家驿 杨乃森 唐 宏 徐朋磊 纪 超

（北京师范大学遥感科学国家重点实验室，北京 100875）

1 引言

深度学习作为机器学习的一个分支，已经在图像处理［1］、自然语言处理［2］、语音识别［3］等领域得到了广泛应用。深度神经网络成功的一个关键因素是它的网络足够深，大量非线性网络层的复杂组合能对原始数据在各种抽象层面上提取特征。然而，由于大多数深度学习模型复杂度高、参数多、透明性低，如黑盒一般［4］，导致人们难以理解其内部工作机制。由于缺乏一定的可解释性，深度学习模型在医学诊断［5］、自动驾驶［6］等决策风险较高领域的应用受到了严重阻碍。近几年来，深度学习模型可解释性研究引起了学术界和企业界的高度关注，人们相继提出各类解释方法来试图解决模型“黑盒”问题，并取得了一些重要进展［4］。

残差网络（Residual Network，简称ResNet）是深度学习领域中的一个里程碑式突破，在很大程度上避免了随着网络层数的增加而产生的梯度消失或梯度爆炸问题，这让训练极深的网络成为可能［7］。梯度提升方法［8］以阶段性策略构建加法模型，将多个基学习器集成为一个更强大的模型。其中决策树常被用于梯度提升方法中的基学习器。端到端的梯度提升网络［9］（End-to-end Gradient Boosting Network，简称EGB-Net）是以神经网络为基学习器，通过逐渐添加新的学习器成为一个集成模型。EGB-Net 可以在不同阶段使用新数据训练新的学习器实现持续学习［10-11］，在一些应用场景中有着一定的优势。EGB-Net 作为集成模型拥有较多的参数，容易产生过拟合问题。对每个学习器施加一个相同的学习率，可以作为防止过拟合的正则化［8］。EGB-Net 和ResNet 的网络结构有相似之处，二者后面的网络单元（学习器或残差块）都在前面网络单元的基础上继续学习，因此二者有一定的可比性。

EGB-Net 的网络结构较复杂，我们对其工作机制的理解不够深入。可视化方法是打开神经网络“黑盒”的常用方法。当前的可视化方法主要包含三类：一是对神经网络学习到的特征进行可视化［12-13］；二是基于热力图［14］或显著图［15］的可视化方法；三是从特征变换、剖分等角度对网络的分类过程进行分析和可视化［16］。本文为了探究EGBNet 的工作机制，希望通过与其他网络的对比，发现它们分类过程的差异。因此本文利用上述第三种可视化方法对EGB-Net 的分类过程进行可视化和分析。我们通过将EGB-Net 与全连接神经网络（Multi-Layer Perceptron，简称MLP）和残差网络的对比，突出EGB-Net 的分类过程、特点和问题。由于EGB-Net 和ResNet 的网络结构有着更多的相似之处，我们利用哑节点对二者的自正则能力进行了对比分析。之后，用可视化方法探索了学习率对EGB-Net 分类过程的影响。最后，通过实际分类任务上的实验，对可视化内容所得结论的正确性进行了验证。

2 EGB-Net网络结构与学习算法

2.1 ResNet

ResNet 是由残差块（残差单元）构建的，残差块的捷径连接结构相当于包含一个天然的恒等映射，可以保留原始信息并减少网络参数。图1 给出了一个残差块示意图，假设该残差块的输入为xl，经过残差函数（weight：权重层，BN：归一化层，ReLU：非线性激活函数层）变换后的值与输入值相加（addition）并激活，作为下一个残差块的输入xl+1。图2（a）是简化表示的拥有3 个残差块的ResNet 示意图。

2.2 EGB-Net

EGB-Net由多个学习器集合而成，每个学习器内部可以是全连接网络或残差网络等基本的网络结构。如图2（b）表示的是由3个学习器组成的EGB-Net，每个学习器是一个残差网络。EGB-Net逐个叠加学习器，在训练新学习器时，前面的学习器已经训练完毕且冻结参数，只对新加的学习器的参数进行更新，参数更新方法可以是梯度下降法。EGB-Net的学习器和ResNet的残差块都基于前面的学习器或残差块继续学习，以提高网络在训练集上的表现。二者主要的区别在于，EGB-Net的学习器是逐个叠加的，每次通过训练新的学习器来优化目前的网络，而ResNet 中所有的残差块是一起训练的。

2.3 EGB-Net的学习算法

由于EGB-Net 作为集成模型参数较多，容易产生过拟合问题。给EGB-Net中的每个学习器施加一个相同的学习率会降低单一学习器的主导地位，从而减小网络过拟合［9］。和神经网络中用来控制参数更新速度的学习率不同，这里的学习率指当前面的学习器训练完成后，在训练后一个学习器时，将前面学习器的输出结果（如softmax 之前的结果）乘以一个小于1的常数。这样可以强行减小前面的学习器将训练样本归为某个类别的概率值，从而让后一个学习器可以“学到更多东西”。当学习率等于1时，即将学习器的输出结果乘以1，相当于不施加学习率。学习率v和学习器的数量M共同决定了模型的性能［9］。当学习率v存在的情况下，EGB-Net的算法如表1所示。

表1 端到端的梯度提升算法Tab.1 End-to-end gradient boosting algorithm

3 分类过程可视化

3.1 EGB-Net特征空间剖分可视化

对于某个分类任务，有时我们只能得到相对较弱的网络作为集成模型的基学习器。为探究此时EGB-Net 的分类效果，我们生成含有1000 个样本点的“同心圆”模拟数据，如图3。随机划分500 个作为训练集，另外500 个作为测试集。该数据分为两个类别，其中橙色点为类别0，蓝色点为类别1。我们使用由5 个弱学习器集成的EGB-Net 对该数据进行训练，每个弱学习器的隐层只有1 个节点。我们以两个MLP 网络作为参照，每个MLP 拥有5 个隐层，其中MLP1 的隐层只有1 个节点，MLP2 的隐层有2 个节点。MLP1 拥有与EGB-Net 差不多的参数量，MLP2 的参数量约是EGB-Net 的2 倍。EGB-Net和2 个MLP 的激活函数均为ReLU 函数，且其他参数设置相同。我们将充分训练后的三个网络对原始特征空间的剖分情况进行可视化，如图4所示。

从图中可以看出，EGB-Net 最后可以将两类数据分好，而与其参数量差不多的MLP1 和参数量更多的MLP2 都不能将数据分好。为了看出EGB-Net将数据划分的过程，进而分析其相对于MLP 的优势，我们将每叠加一个学习器后EGB-Net 对原始特征空间的剖分情况进行可视化，如图5所示。

可以看到，随着学习器的叠加，网络对两类数据的可分情况逐渐变好。后面的学习器在前面的基础上继续对特征空间进行剖分，且主要针对前面没有分好的部分，逐步提高网络对数据的拟合能力。对于MLP 等整体进行训练的网络，其网络中的参数是互相影响的，没有使各个部分相对独立的机制，难以将复杂任务分解成多个更简单的任务。在此实验中，虽然MLP1 拥有5 个隐层，但由于隐层只含有1 个节点，不能将特征空间变换到更高的维度进行剖分，最终只划出一条线，明显不能将数据分好。同样对于隐层含有2个节点的MLP2，只能对特征空间进行2 维的变换，最终也不能将数据分好。而EGB-Net 的每个学习器虽然只有1 个隐节点，但是后面的学习器可以基于前面学习器的划分结果继续对特征空间进行划分，因此最后可以完成分类。EGB-Net的分类机制可以将复杂的任务分解为多个子任务，这种分阶段的训练方式在面对一些分类任务时，往往有其优势。

3.2 EGB-Net特征变换可视化

为进一步探究EGB-Net 分类过程的特点，我们生成含有1000个样本点的“螺旋线”模拟数据，其分类难度比“同心圆”数据较大，如图6。同样随机划分500 个作为训练集，另外500 个作为测试集。我们使用由10 个较强学习器组成的EGB-Net 对该数据进行训练，每个学习器有1个残差块，每个残差块有2 个隐层，每个隐层有10 个节点。我们以ResNet作为参照，设置ResNet 拥有10 个残差块，每个残差块有2 个隐层，每个隐层同样有10 个节点。两个网络的激活函数均设置为ReLU 函数，且其他参数设置相同。两个网络均得到充分的训练。

网络训练完成后，我们将这1000个样本点重新输入到训练好的网络中。对于EGB-Net，我们将每叠加1 个学习器后样本点的状态进行可视化，如图7（a）所示。可以观察在经过第1 个、前2 个、前3 个、......、前10 个学习器的特征变换后，两类样本线性可分的程度；对于ResNet，我们将每叠加1个残差块后样本点的状态进行可视化，如图7（b）所示。可以观察在经过第1 个、前2 个、前3 个、……、前10个残差块的特征变换后，两类样本线性可分的程度。由于EGB-Net 和ResNet 整体上都拥有10 个相同结构的残差块，这样的可视化方式可以较公平地比较二者分类过程的差异。

从可视化结果可以看出，对于EGB-Net，螺旋线数据在经过第一个学习器的特征变换后，其形态就已经发生了很大的变化，当叠加到3 个学习器时基本上达到了线性可分的状态，此时再叠加更多的学习器，数据的形态也不再发生明显改变。对于ResNet，螺旋线数据在经过前几个残差块的特征变换后，其形态变化并不显著，到第6个残差块还可以大致看出螺旋线的形状。实验和观察结果表明：EGB-Net 中的每个学习器，有着“努力”把数据分好的倾向。当学习器较强时，前面的学习器对分类任务所做的贡献更大，后面的学习器主要对前面没有分好的细微部分进行调整。而ResNet 中前面的残差块并没有“努力”把数据分好的倾向，而是把更多的分类任务留给了后面，后面的残差块对分类任务所做的贡献更大。

由于EGB-Net中的每个学习器会“努力”进行分类，每叠加一个学习器后，当前的网络都会“努力”拟合训练数据，因此网络容易出现过拟合。相比之下，ResNet 中的残差块并没有都在“努力”进行分类，这会使网络不那么容易过拟合，然而也使得残差块可能存在着冗余。

3.3 EGB-Net和ResNet哑节点数量比较

上述两个网络隐层使用的非线性激活函数为ReLU 函数。隐层节点在进行激活时，若特征空间中的所有特征点在输入ReLU 函数时均小于0，此时该隐层节点对特征空间中的所有特征点均不激活，则称该节点为真哑节点。若特征空间中的所有特征点在输入ReLU 函数时均不小于0，此时该隐层节点对特征空间中的所有特征点均激活，则称该节点为伪哑节点［16］。真哑节点与伪哑节点均不对特征空间进行剖分，这类节点统称为哑节点，将出现哑节点的情况称为自正则［18］。哑节点的数量代表了网络自正则能力的大小。

为进一步了解EGB-Net和ResNet分类时网络工作机制的差异，我们对这两种网络分别进行1000次实验以统计其哑节点数量。实验用到的EGB-Net、ResNet以及螺旋线数据均与本文3.2中使用的相同。经过训练，EGB-Net 和ResNet 在1000 次实验中的平均训练精度均达到99%以上，平均测试精度均达到95%以上。网络训练完成后统计它们的哑节点数量，如图8 所示。图中展示的是1000 次训练中，每次训练结束后两个网络各自的哑节点数量（横轴）与出现频数的关系（纵轴）。

图中EGB-Net 哑节点数量的区间为［1，16］，出现频数最多的哑节点数量为8 个，出现了138 次。ResNet 哑节点数量的区间为［2，43］，出现频数最多的哑节点数量为11个，出现了119次；经统计，EGBNet 的平均哑节点数量为7.59 个，ResNet 的平均哑节点数量为11.22 个。结果表明，当EGB-Net 和ResNet 网络内部残差块的数量和结构相同时，训练后的EGB-Net 往往比ResNet 拥有较少数量的哑节点，所以其自正则能力相对较弱。由于EGB-Net 有更多的节点对特征空间进行了剖分，网络对训练数据做了更细致的拟合，因此更容易出现过拟合。

3.4 有无学习率的EGB-Net分类过程可视化

前面提到在EGB-Net中，后面的学习器在很大程度上依赖前面学习器的分类结果，并对前面学习器的分类结果进行调整。若学习器较强，前面的学习器对分类结果影响较大，后面的学习器在调整前面学习器的分类结果时会比较困难，此时更容易出现过拟合。在EGB-Net中加入学习率可以在一定程度上缓解过拟合。为探究学习率对EGB-Net分类过程的影响，我们使用3.2中用到的螺旋线模拟数据，并生成两个除学习率外，其他网络结构和参数均相同的EGB-Net。每个EGB-Net由5个更强的学习器组成，每个学习器有3个残差块，每个残差块2个隐层，隐层有10个节点。其中一个EGB-Net的学习率为1（即不设置学习率），另一个EGB-Net的学习率为0.1。

通过绘制训练曲线可以观察每叠加一个学习器后两个网络的表现，图9 展示了当上述两个网络叠加到1 个、3 个和5 个学习器时，它们在训练集和测试集上各自的精度和损失，其中每列从上到下为n个学习器时的训练曲线，n=1，3，5。这里我们只对两网络分类过程的差异进行讨论，暂不讨论二者在测试集上的表现。

从训练曲线可以看到，第1 个学习器就可以使训练精度较高，训练损失接近于0，此时已基本可以将两类数据分开。当学习率为1，叠加到第3 个学习器时训练曲线接近于一条直线，此时后面的学习器对分类的影响很小；当学习率为0.1，叠加到第3 个学习器时训练曲线不再是一条直线，说明此时后面的学习器可以对分类结果产生更大的影响。

为进一步探究学习率对EGB-Net分类过程的影响，我们使用前面的可视化方法，将每叠加一个学习器，学习率为1和学习率为0.1的EGB-Net把样本点特征变换后的形态，和对原始特征空间的剖分情况进行可视化，如图10所示。图中按从左到右的顺序，第1 列和第3 列分别是学习率为1 时，每叠加一个学习器，网络对样本点特征变换的结果和对原始特征空间剖分的结果；第2 列和第4 列分别是学习率为0.1时，每叠加一个学习器，网络对样本点特征变换的结果和对原始特征空间剖分的结果。

从图中可以看出，随着学习器的叠加，没有设置学习率的EGB-Net样本点的形态变化并不显著，且对原始特征空间的剖分变化不大。设置了0.1的学习率之后，样本点的形态变化更显著，且对原始特征空间的剖分变化更大。这表明学习率的加入，使得后面的学习器对前面学习器的分类结果进行了更多的调整。若不设置学习率，对于前面错分的部分，后面的学习器需要预测出更大的正确类别的概率值才能将错分部分纠正，此时后面的学习器调整起来更加困难。学习率的大小很大程度上决定了后面的学习器对分类结果的调整能力，当EGB-Net中的学习器较强时，往往需要设置较小的学习率。

4 实验验证

4.1 数据与模型

对于可视化得到的关于EGB-Net分类过程的结论和发现，我们通过如下实验对其正确性进行验证。应用深度神经网络从遥感影像上提取感兴趣的地物目标，是近年来相关研究的热点。建筑物作为主要的人造地物，地震等自然灾害对其的破坏经常会造成生命和财产的损失。从遥感影像上提取建筑的分布情况，可以为灾损评估提供重要信息。基于此背景，我们以2010 年青海省玉树地震发生前的玉树县城区（结古镇）高分辨率遥感影像为实验数据，如图11。该影像来源于美国Quickbird卫星。我们将影像裁剪为64 个2048×2048 个像元大小的影像块，随机划分32个为训练集，另外32个为测试集。

我们使用以U-NASNetMobile［9］为基学习器的GeoBoost模型［9］进行实验，它是一个端到端的梯度提升网络模型。其第一个学习器已经使用建筑减灾和应急管理数据集（DREAM-B）［9］训练完毕，用于玉树遥感影像中建筑物的初步识别。我们首先使用只有这一个学习器的GeoBoost 模型在测试集上进行预测，然后使用上述训练数据依次训练第2个和第3个学习器，并叠加到原模型中。为了验证学习率的作用，我们设置对照实验，其中一个模型在训练新的学习器时均不设置学习率（即学习率等于1），另一个模型在训练新的学习器时均设置学习率为0.1。除学习率外，二者的其他参数设置相同。

4.2 实验结果定量分析

我们使用精度度量指标IoU（Intersection over Union：重叠度）评估模型的训练精度和测试精度。IoU 被定义为：

其中Prediction 为预测结果，GroundTruth 为真值标签。此外，也提供另一种精度度量指标OA（Overall Accuracy：总体精度）用于参考。有无学习率的GeoBoost 模型在训练第2 个和第3 个学习器时，训练集和测试集上的IoU 如图12 所示；三个阶段的模型在测试集上的IoU 和OA 值如表2所示。

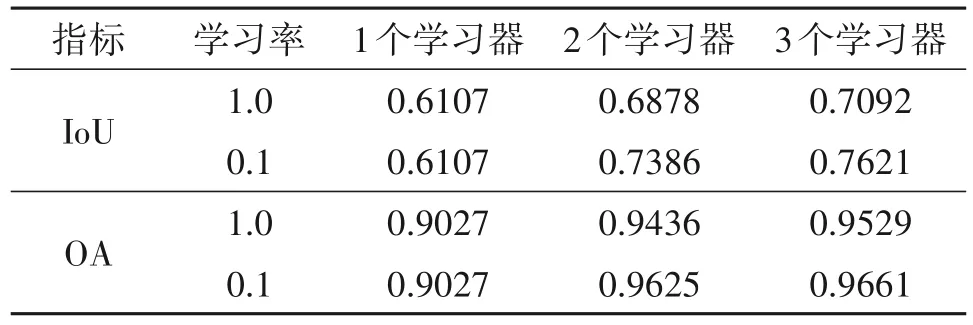
表2 模型在不同阶段的测试精度Tab.2 Test accuracy of the model at different stages

从IoU 曲线可以看出，第3 个学习器在前面的基础上继续提高了模型的训练集和测试集精度，且训练第3 个学习器时模型收敛更快。这说明第2 个学习器难以利用新数据充分调整第1个学习器的分类结果，所以需要更多的学习器。EGB-Net 这种分阶段的训练方式相当于把复杂的任务分解，交给多个学习器逐步完成。

结合训练曲线和表格可以看到，学习率为0.1的模型在测试集上的精度明显高于不设置学习率的模型精度，说明学习率可以提高基于EGB-Net 的模型的泛化能力。值得一提的是第2 个和第3 个学习器使用了上述训练集数据进行训练，所以拥有2 个和3 个学习器的模型相比原模型总体上使用了更多的训练数据，因此其在指标上的提升是可以预期的，这也体现了基于EGB-Net的模型的特点，即可以在不同阶段利用新数据训练新的学习器，对原始模型进行调整，从而有可能提高模型的泛化能力。

4.3 实验结果定性分析

图13 显示了当学习率为1 时，不同阶段的模型在测试集上的一些语义分割结果。图14 显示了当学习率为1 时，拥有3 个学习器的模型；以及当学习率为0.1时，拥有2个和3个学习器的模型在测试集上的一些语义分割结果，其中lr 表示学习率。图中的每一行为同一地点，最左列的红色标记是建筑物的真值标签，右边三列的绿色标记是模型的预测结果，黄色圆圈指示了其中值得关注的部分。

对比图13 可以看出，只有1 个学习器的原模型，其预测结果有更多的粘连和错误分类的部分，第2 个学习器在一定程度上对此进行了调整，但不可避免的存在调整错误的情况，拥有3 个学习器的模型给出了更好的预测结果。对比图14可以看出，当学习率为0.1 时，拥有3 个学习器的模型同样给出了更好的预测结果，相比之下不设置学习率的模型预测结果要明显差一些。需要注意的是这些可视化结果仅仅作为参考，不同阶段模型产生的微小差异也有可能是由训练过程的随机性和权值随机初始化导致的，前面的定量分析结果更为可靠。

本节用定量和定性的方法分析了基于EGB-Net的GeoBoost 模型在实际分类任务上的特点，实验结果验证了本文第3节通过可视化得到的相关结论。

5 结论

本文利用特征变换和特征空间剖分两种可视化方法，对EGB-Net 的分类过程、优点、问题等方面进行了探索，有以下发现和结论：EGB-Net可以逐步完成分类任务，当一个分类任务较复杂而单个网络难以完成时，这种分阶段的训练方式往往可以发挥其优势。由于EGB-Net的每个学习器都会“努力”去进行分类，使得网络中哑节点的数量较少，其自正则能力相对较弱，因此网络容易出现过拟合问题。通过对设置了学习率的EGB-Net分类过程进行可视化，可以直观地看出学习率对其分类过程的影响。学习率增加了后面的学习器对分类结果的调节能力，从而平衡了各个学习器对分类结果的影响程度。最后通过实际分类任务上的实验对可视化的内容从结果层面进行了验证，而可视化内容有助于解释我们看到的实验结果。

文中将学习率设置为0.1来说明其作用，这不一定是其最佳的学习率，也是本文研究的不足之处。如何为EGB-Net找到适合的学习率是值得进一步研究的内容。在与EGB-Net 对比的过程中，我们发现ResNet 中的残差块没有都在“努力”进行分类，残差块可能存在冗余，如何在保证网络性能的前提下，减少残差块数量以精简网络是另一个值得探讨的内容。